Geum.ru

Робоча навчальна програма для студентів спеціальності 070201 "радіофізика І електроніка"

Вид материалаДокументы

Содержание


Зав. Кафедри
Укладачі : кандидат фізико-математичних наук, доцент Кривошея С.А.
Голови НМК радіофізичного факультету
Мета і завдання навчальної дисципліни "Математичний аналіз"
Предмет навчальної дисципліни "Математичний аналіз"
Вимоги до знань та вмінь.
Студент повинен вміти
Місце в структурно-логічній схемі спеціальності.
Контроль знань
Шкала оцінювання
Тематичний план лекцій і практичних занять
Всього за i-й семестр
Подобный материал:
Київський національний університет імені Тараса Шевченка

Радіофізичний факультет




Кафедра математики

і теоретичної радіофізики


Укладачі: к. ф.-м. н., доцент Кривошея С.А.

к. ф.-м. н., доцент Моторна О.В.


МАТЕМАТИЧНИЙ АНАЛІЗ



РОБОЧА НАВЧАЛЬНА ПРОГРАМА


для студентів спеціальності

070201 “радіофізика і електроніка”


Затверджено

на засіданні кафедри математики

і теоретичної радіофізики

Протокол № __6___

від „12” травня 2010 р.

Зав. Кафедри


_____________ Висоцький В.І.


Декан радіофізичного факультету

_____________ Анісімов І.О.


КИЇВ – 2010


Робоча навчальна програма з дисципліни «Математичний аналіз».

Укладачі : кандидат фізико-математичних наук, доцент Кривошея С.А.,


кандидат фізико-математичних наук, доцент Моторна О. В.


Лектори: кандидат фізико-математичних наук, доцент Кривошея С.А.,


кандидат фізико-математичних наук, доцент Моторна О. В.


Викладачі: кандидат фізико-математичних наук, доцент Сугакова О.В.

асистент Горбовцова Н.В.

асистент Жеребко Т.М.

асистент Іваненко Д.О.

асистент Крюкова Г.В.

асистент Масютка О.Ю.

асистент Усольцева О.С.


Погоджено

з науково-методичною комісією

«____» ______________ 20__р.


Голови НМК радіофізичного факультету




________________________ Обуховський В.В.


ВСТУП


Дисципліна "Математичний аналіз" є базовою нормативною дисципліною для спеціальності "радіофізика і електроніка", що вивчається в І та ІІ семестрах в обсязі 10 кредитів (за Європейською Кредитно-Трансферною Системою ECTS), в тому числі 210 годин аудиторних занять, з них 105 годин лекцій, 105 годин практичних занять і 144 години самостійної роботи ( І семестр: лекції - 54, практичні - 54, самостійна робота - 72; ІІ семестр: лекції - 51, практичні - 51, самостійна робота - 72) і закінчується іспитами у І-му та ІІ-му семестрах.


Мета і завдання навчальної дисципліни "Математичний аналіз": ознайомлення та оволодіння сучасними математичними методами, теоретичними положеннями та основними застосуваннями методів математичного аналізу у фізиці та радіофізиці, сприяння розитку логічного та аналітичного мислення студентів.


Предмет навчальної дисципліни "Математичний аналіз" включає основні методи та моделі математичного аналізу (диференціального та інтегрального числення). Всі математичні поняття, що вивчаються, ілюструються застосуваннями.


Вимоги до знань та вмінь.

Студент повинен знати: основні поняття математичного аналізу такі як границя та неперервність функції, диференційовність, екстремум, первісна функції та інтеграл, елементи математичної теорії поля.

Студент повинен вміти: обирати математичні методи, прийоми математичного анлізу для розв'язання фізичних задач та набути навичок самостійного використання і вивчення літератури з математичних дисциплін.


Місце в структурно-логічній схемі спеціальності.

Нормативна навчальна дисципліна "Математичний аналіз" є складовою циклу професійної підготовки фахівців освітньо-кваліфікаційного рівня "бакалавр", є базовою для вивчення таких дисциплін як "Теорія ймовірностей", "Диференціальні рівняння", "Математична фізика", "Аналітична геометрія", "Чисельні методи".


Контроль знань


Курс математичного аналізу складається з 3-х змістових модулів (ЗМ-1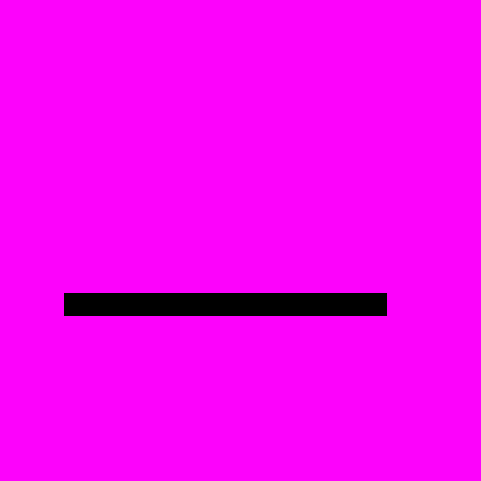ЗМ-3) у першому семестрі і 3-х змістовних модулів (ЗМ-4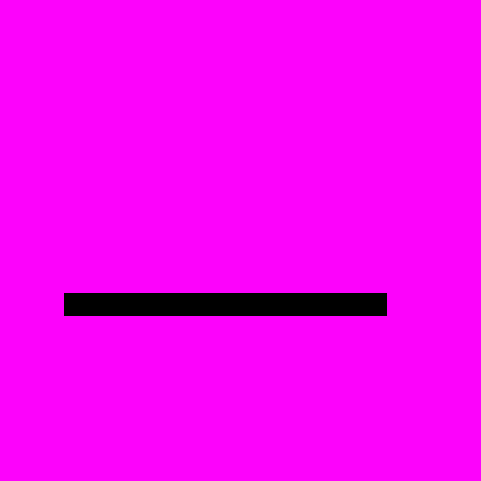ЗМ-6) у другому семестрі.

Навчальним планом на вивчення курсу відведено 5 кредитів (54 години лекцій, 54 години практичних занять, 36 годин СРС) у першому семестрі і 5 кредитів (51 година лекцій, 51 година практичних занять, 36 годин СРС) у другому семестрі .

Контроль знань студентів здійснюється за модульно-рейтинговою системою.


У першому семестрі передбачені :
  1. 3 підсумкові модульні контрольні (ПМК-1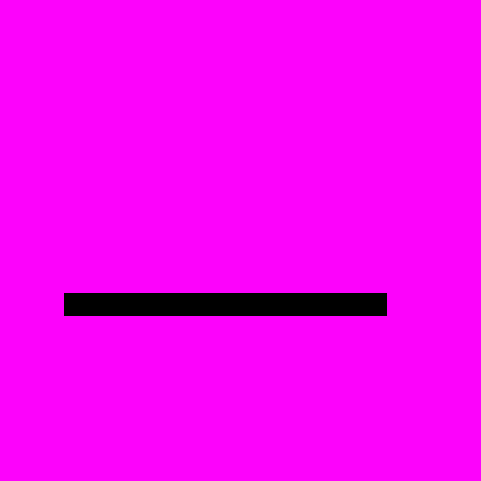ПМК-3);
  2. 3 контрольні роботи СРС;
  3. комлексний підсумковий модуль-іспит (КПМ-І).


У другому семестрі передбачені:
  1. 3 підсумкові модульні контрольні (ПМК-4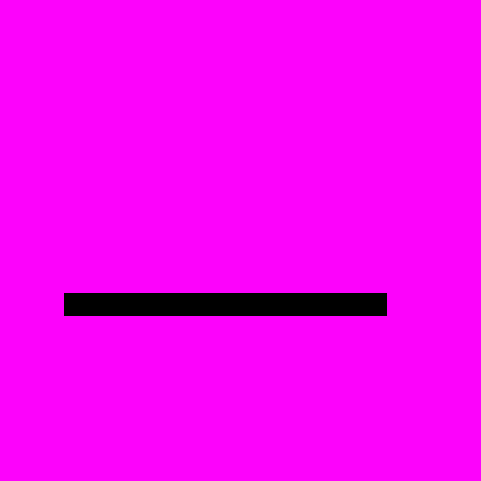ПМК-6);
  2. 3 контрольні роботи СРС;
  3. комлексний підсумковий модуль-іспит (КПМ-ІІ).



Підсумкова оцінка (ПО) розраховується за накопичувальною системою


І-й семестр



Максимальна кількість балів
Вид контролю

ПМК-1
ПМК-2
ПМК-3
КПМ-І
ПО-І

За модульну контрольну роботу
10
5
10
40
100

за активність на заняттях, виконання завдань СРС, участь в математичних олімпіадах
10
5
20






Всього
20
10
30
40
100



ІІ-й семестр



Максимальна кількість балів
Вид контролю

ПМК-4
ПМК-5
ПМК-6
КПМ-ІІ
ПО-ІІ

За модульну контрольну роботу
5
5
10
40
100

за активність на заняттях, виконання завдань СРС, участь в математичних олімпіадах
5
5
30






Всього
10
10
40
40
100



Структура підсумкових модульних контролів


ПМК-1, ПМК-2,

ПМК-4, ПМК-5:

  1. Теоретичне питання - 1 бал
  2. Теоретичне питання - 1 бал
  3. Практичне завдання - 1 бал
  4. Практичне завдання - 1 бал
  5. Практичне завдання - 1 бал



ПМК-3, ПМК-6:

  1. Теоретичне питання - 2 бали
  2. Теоретичне питання - 2 бали
  3. Практичне завдання - 2 бали
  4. Практичне завдання - 2 бали
  5. Практичне завдання - 2 бали



ШКАЛА ОЦІНЮВАННЯ



За шкалою Університету (100-бальною системою)
Оцінка за національною шкалою та шкалою Університету

90-100
відмінно - 5

85-89
добре - 4

75-84

65-74
задовільно - 3

60-64

35-59
незадовільно - 2

1-34
незадовільно - 2



Тематичний план лекцій і практичних занять


I-й семестр



№ лекції

(практич. заняття)

Назва лекції

( тема практичного заняття )
Кількість годин

лекції
практ.

заняття
самост.

робота
контр.

модуль-на

робота
інші

форми

контро-лю



Змістовий модуль 1


Диференціальне числення СФСА



1
Границя числової послідовності (ч.п.)
2












2
Основні теореми теорії границь ч.п.
2












3
Границя і неперервність СФСА в точці
2












4
Визначені границі. Локальні властивості неперервних функцій
2












5
Асимптотична символіка. Класифікація

точок розриву
2












6
Властивості функцій класу С[a,b]
2












7
Основні теореми про похідну функції
2












8
Диференційовність і диференціал

Теореми про середнє значення
2



2






9
Правило Лопіталя. Похідні і диференціали вищих порядків
2



2






10
Формула Тейлора.
2












11
Дослідження функцій
2



2






1
Метод математичної індукції. Біном Ньютона ( самостійна робота з елемен-

тарної математики)



2
2






2
Комплексні числа



2
4






3
Границя ч.п.



2









4
Границя ч.п.



2
2






5
Границя СФСА



2
2






6
Границя СФСА



2
2






7
Асимптотична символіка



2
2






8
Класифікація точок розриву функції



2
4






9
Техніка диференціювання



2
4






10
Техніка диференціювання. Диференціал і формула малих приростів



2









11
Похідні і диференціали вищих порядків Формула Тейлора



2
2






12
Формула Тейлора. Правило Лопіталя



2
2






13
Дослідження функцій і побудова графіків



2
4









ВСЬОГО
22
26
36
4





Змістовий модуль 2


Диференціальне числення функції векторного аргументу (ФВА)



12
Метричні простори. Збіжність в

2












13
Теорема Банаха (принцип нерухомої точки)
2












14
Границя і неперервність ФВА
2



2






15
Диференційовність ФВА
2












16
Диференційовність складних ФВА
2












17
Диференційовні відображення

2



2






18
Умови існування і диференційоіність неявних ФВА
2



2






19
Формула Тейлора для ФВА
2



2






20
Локальні екстремуми ФВА
2



2






21
Умовні локальні екстремуми ФВА
2












22
Умовні локальні екстремуми ФВА
2












14
Техніка диференціювання ФВА



2
2






15
Техніка диференціювання ФВА



2
2






16
Техніка диференціювання неявних ФВА



2
2






17
Заміна змінних у диференціальних виразах



2









18
Заміна змінних у диференціальних виразах



2
2






19
Локальні екстремуми ФВА



2









20
Умовні локальні екстремуми ФВА



2












ВСЬОГО
22
14
18
2





Змістовий модуль 3.


Інтегральне числення СФСА



23
Невизначений інтеграл
2












24
Інтегрування раціональних функцій
2












25
Інтеграл Рімана

2



2






26
Інтеграл Рімана
2



2






27
Методи обчислення інтеграла Рімана
2












21
Основні методи інтегрування



2
2






22
Інтегрування раціональних функцій



2
2






23
Інтегрування ірраціональних функцій



2
2






24
Інтегрування трансцендентних функцій



2
4






25
Обчислення інтеграла Рімана



2









26
Обчислення інтеграла Рімана



2









27
Обчислення інтеграла Рімана



2
4









ВСЬОГО
10
14
18
2






ВСЬОГО ЗА I-Й СЕМЕСТР
54
54
72
8





II-й семестр


Змістовий модуль 4


Невласні інтеграли та інтеграли, залежні від параметра



1
Невласні інтеграли (н.і.). Ознаки збіжності н.і. від невід'ємних функцій



2
2






2
Ознаки збіжності невласних інтегралів

від знакозмінних функцій
2












3
Власні та невласні інтеграли, залежні

від параметра
2



2






4
Власні та невласні інтеграли, залежні

від параметра
2



2






5
Ейлерові інтеграли
2












6
Інтеграл і перетворення Фур'є
2



2






1
Невласні інтеграли



2









2
Невласні інтеграли



2
2






3
Інтеграли, залежні від параметра



2
2






4
Інтеграли, залежні від параметра



2
2






5
Ейлерові інтеграли



2
4






6
Інтеграл і перетворення Фур'є



2
4









ВСЬОГО
12
12
18
2





Змістовий модуль 5


Інтегральне числення функцій векторного аргументу (ФВА).

Елементи математичної теорії поля


7
Поняття міри Жордана в . Означен-

ня m-кратного інтеграла
2



4






8
Властивості і обчислення кратних інтеграпів
2












9
Заміна змінних в кратних інтегралах
2



4






10
Криволінійні інтеграли 1-го і 2-го родів
2












11
Поверхневі інтеграли 1-го і 2-го родів
2












12
Інтегральні теореми Гріна, Остроградського, Стокса
2












13
Інтегральні теореми Гріна, Остроградського, Стокса
2












14
Застосування кратних, криволінійних і поверхневих інтегралів
2












15
Скалярні і векторні поля. Похідна за

напрямом і градієнт. Потік і дивергенція
2




2






16
Циркуляція і ротор векторного поля
2



2






17
Типи векторних полів. Набла-символіка
2



2






18
Запис основних диференціальних операцій теорії поля в ортогональній криволінійній системі координат (ОКСК)
2



4






7
Обчислення кратних інтегралів




2
2






8
Обчислення кратних інтегралів




2
2






9
Заміна змінних в кратних інтегралах




2









10
Заміна змінних в кратних інтегралах




2
2






11
Обчислення криволінійних інтегралів




2









12
Обчислення поверхневих інтегралів



2









13
Обчислення поверхневих інтегралів



2
2






14
Формула Гріна. Інтегрування повних диференціалів



2









15
Інтегральні теореми Остроградського, Стокса




2









16
Інтегральні теореми Остроградського, Стокса




2
2






17
Похідна за напрямом і градієнт скалярного поля. Обчислення потоку і дивергенції



2
2






18
Циркуляція і ротор векторного поля.

Застосування теорем Остроградського

і Стокса



2
2






19
Набла-символіка



2
2






20
Набла-символіка



2
2









ВСЬОГО
24
28
36
4





Змістовий модуль6


Числові та функціональні ряди




№ лекції

(практич. заняття)

Назва лекції

( тема практичного заняття )
Кількість годин

лекції
практ.

заняття
самост.

робота
контр.

модуль-на

робота
інші

форми

контро-лю

19
Ознаки збіжності числових рядів з невід'ємними членами
2



2






20
Ознаки збіжності знакозмінних рядів
2












21
Функціональні послідовності і ряди
2



2






22
Властивості рівномірнозбіжних

функціональних послідовностей і рядів
2



2






23
Степеневі ряди. Ряд Тейлора
2












24
Ряди Фур'є в Q[a,b]

2



2






25
Тригонометричні ряди Фур'є
2












26
Тригонометричні ряди Фур'є
2












21
Числові ряди з невід'ємними членами



2
2






22
Знакозмінні числові ряди



2









23
Функціональні послідовності і ряди



2
4






24
Степеневі ряди



2
4






25
Тригонометричні ряди Фур'є



2









26
Тригонометричні ряди Фур'є



2












ВСЬОГО
16
12
18
2






ВСЬОГО ЗА II-Й СЕМЕСТР
51
51
72
8






ВСЬОГО ЗА НАВЧАЛЬНИЙ РІК
105
105
144
16




>