Робоча навчальна програма для студентів спеціальності 070201

Вид материала

Документы

Содержание Лектор: к.ф-м.н., ас. Зайцева Л.Л.Викладачі Підпис голови НМК факультету/ інституту Метою і завданням навчальної дисципліни Предмет навчальної дисципліни Вимоги до знань та вмінь. Місце в структурно-логічній схемі спеціальності. Система контролю знань та умови складання іспиту. Навчально-тематичний план лекцій і практичних занять Назва теми Завдання для самостійної роботи ( Завдання для самостійної роботи ( Завдання для самостійної роботи ( Завдання для самостійної роботи ( Завдання для самостійної роботи ( Типове завдання модульної контрольної роботи № 1 Завдання для самостійної роботи ( Завдання для самостійної роботи ( Завдання для самостійної роботи ( Завдання для самостійної роботи ( Завдання для самостійної роботи ( ... Полное содержание

Подобный материал:

• Робоча навчальна програма для студентів спеціальності 070201 «Радіофізика І електроніка», 386.16kb.
• Робоча навчальна програма для студентів спеціальності 030. 302 "Реклама та зв'язки, 310.69kb.
• Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 176.29kb.
• Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 280.46kb.
• Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 321.43kb.
• Робоча навчальна програма для студентів спеціальності 040103 геологія Затверджено, 628.51kb.
• Робоча навчальна програма для студентів спеціальності 030301 „Журналістика Затверджено, 278.32kb.
• Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 208.66kb.
• Робоча навчальна програма для студентів спеціальності 030401 «Право» Затверджено, 944.73kb.
• Робоча навчальна програма для студентів спеціальності "060101 Правознавство" Затверджено, 408.94kb.

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ імені ТАРАСА ШЕВЧЕНКА


Радіофізичний факультет


радіофізичний факультет

кафедра математики

та теоретичної радіофізики


Укладач: к. ф.-м. н. асистент Зайцева Л.Л.


ПРИКЛАДНІ МЕТОДИ ВИЩОЇ МАТЕМАТИКИ


РОБОЧА НАВЧАЛЬНА ПРОГРАМА


для студентів спеціальності 070201 " Радіофізика і електроніка ”


Затверджено

на засіданні кафедри

Протокол № ___

від „___”___________200__р.

Зав. кафедри

_____________ ____________________

Підпис Прізвище, ініціали

Декан факультету

_____________ ____________________


КИЇВ-2008


Робоча навчальна програма з дисципліни «Прикладні методи вищої математики».

Укладач: кандидат фізико-математичних наук,

асистент Зайцева Людмила Леонтіївна


Лектор: к.ф-м.н., ас. Зайцева Л.Л.


Викладачі: к.ф-м.н., доц. Єфіменко С.В.

ас. Масютка О.Ю.

ас. Жеребко Т.М.


Погоджено

з науково-методичною комісією

«____» ______________ 200__р.


___________________________

Підпис голови НМК факультету/ інституту


ВСТУП

Дисципліна «Прикладні методи вищої математики» є базовою нормативною дисципліною для спеціальності «радіофізика і електроніка», яка читається в I семестрі в обсязі 3 кредитів, в тому числі 54 години аудиторних занять, з них 18 годин лекцій, 36 годин практичних занять, і 54 години самостійної роботи. Закінчується іспитом.


Метою і завданням навчальної дисципліни «Прикладні методи вищої математики» є ознайомлення та оволодіння основними математичними поняттями, методами, теоретичними положеннями, необхідними для вивчення базових фізичних курсів.


Предмет навчальної дисципліни «Прикладні методи вищої математики» включає в себе вибіркові методи математичного аналізу, аналітичної геометрії, лінійної алгебри, теорії функцій комплексної змінної, теорії диференціальних рівнянь та комбінаторики.


Вимоги до знань та вмінь.

Студент повинен знати: основні поняття векторної алгебри, теорії диференціювання та інтегрування функцій однієї змінної; елементи теорії рядів, теорії диференціювання функцій багатьох змінних, теорії функцій комплексної змінної, теорії диференціальних рівнянь та комбінаторики.

Студент повинен вміти: застосовувати засвоєні методи вищої математики для розв’язання математичних і фізичних задач, а також застосувати отримані знання при аналізі фізичних явищ.


Місце в структурно-логічній схемі спеціальності. Нормативна навчальна дисципліна «Прикладні методи вищої математики» є складовою циклу професійної підготовки фахівців освітньо–кваліфікаційного рівня «бакалавр», є математичним фундаментом для вивчення загальних курсів фізики, а також є допоміжною для вивчення таких спеціальних дисциплін як "математичний аналіз", "диференціальні рівняння" тощо.


Система контролю знань та умови складання іспиту. Навчальна дисципліна «Прикладні методи вищої математики» оцінюється за модульно-рейтинговою системою. Вона складається з 2 модулів.

Результати навчальної діяльності студентів оцінюються за 100 - бальною шкалою за семестр.

Форми поточного контролю: перевірка виконання домашніх завдань, оцінювання активної роботи студента на практичних заняттях, виконання задач підвищеної складності (самостійна робота).

Модульний контроль: 2 модульні контрольні.

Система контролю знань студента за кожний змістовий модуль.

Форма роботи	Активність студента на практичних заняттях	Підсумкова контрольна робота	Разом (підсумкова оцінка)
Максимальна оцінка в балах	10	20	30

За результатами семестру студент отримує підсумкову оцінку за 100-бальною системою, яка розраховується як сума оцінок за кожен з двох модулів у семестрі та оцінки за іспит за наступною формулою.

І семестр

	Змістовий модуль 1 ( ЗМ1 )	Змістовий модуль 2 ( ЗМ2 )	Іспит (КПМ)	Разом (підсумкова оцінка)
Оцінка (бали)	30	30	40	100

Розрахунок підсумкової оцінки за семестр: ПО= ЗМ₁+ ЗМ₂ + КПМ .

При цьому, кількість балів відповідає оцінці:

1-34 – «незадовільно» з обов’язковим повторним вивченням дисципліни;

35-59 – «незадовільно» з можливістю повторного складання;

60-64 – «задовільно» («достатньо») ;

65-74 – «задовільно»;

75 - 84 – «добре»;

85 - 89 – «добре» («дуже добре»);

90 - 100 – «відмінно».

Шкала відповідності

За 100-бальною шкалою	Оцінка за національною шкалою
	І семестр
90 – 100	5	відмінно
85 – 89	4	добре
75 – 84
65 – 74	3	задовільно
60 – 64
35 – 59	2	незадовільно
1 – 34

Якщо за результатами модульно-рейтингового контролю студент отримав в сумі за перший і другий змістові модулі (ЗМ₁+ ЗМ₂) менше ніж 36 балів, то студент не допускається до іспиту і вважається таким, що не виконав усі види робіт, які передбачаються навчальним планом з дисципліни «Прикладні методи вищої математики».


НАВЧАЛЬНО-ТЕМАТИЧНИЙ ПЛАН ЛЕКЦІЙ І ПРАКТИЧНИХ ЗАНЯТЬ

І семестр

№ теми	Назва теми	Кількість годин
		Лекції	Практичні	Самостійна робота
ЗМІСТОВИЙ Модуль 1.
1	Векторна алгебра	4	4	8
2	Диференціальне та інтегральне числення функцій однієї змінної	4	8	14
Модульна контрольна робота 1			2
ЗМІСТОВИЙ Модуль 2.
3	Застосування диференціального та інтегрального числення	2	6	8
4	Спеціальні розділи вищої математики	8	14	24
Модульна контрольна робота 2			2
Всього		18	36	54

Загальний обсяг 108 год.

в тому числі:

Лекції – 18 год.

Практичні – 36 год.

Самостійна робота - 54 год.


І СЕМЕСТР


змістовий МОДУЛЬ І.


ТЕМА 1. Векторна алгебра (8 год.)


Лекція 1. Визначники другого та третього порядків, їх властивості. Вектори. Лінійні операції над векторами, їх властивості.


Означення визначника другого, третього порядків. Властивості визначників. Означення вектора на прямій, на площині, в просторі. Лінійні операції над векторами, їх властивості. Базис на прямій, на площині в просторі. Ортонормований базис. Координати вектора в базисі.


Завдання для самостійної роботи (2 год.)

1. Опрацювання матеріалів лекції.

2. Опрацювання матеріалу на тему „ Заміна координат вектора при заміні базису. Інші системи координатна на площині, в просторі: полярна, сферична, циліндрична. ”

Література [1,3,10,13,19,22].


Практичне заняття 1. Визначники другого та третього порядків, їх властивості. Вектори. Лінійні операції над векторами, їх властивості.

1. Обчислення визначників другого та третього порядків.
   
2. Вектор, координати вектора. Лінійні операції над векторами. Координати лінійної комбінації векторів. Колінеарні вектори.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [1,3,10,13,19,22].


Лекція 2. Скалярний добуток векторів, його властивості. Векторний добуток векторів, його властивості. Мішаний добуток векторів, його властивості. Подвійний векторний добуток.


Означення скалярного добутку, його властивості. Вираз скалярного добутку через координати векторів. Геометричні властивості скалярного добутку. Означення правої, лівої трійки векторів. Означення векторного добутку. Властивості векторного добутку. Вираз векторного добутку через координати векторів. Означення мішаного добутку, його властивості. Вираз мішаного добутку через координати векторів. Подвійний векторний добуток.


Завдання для самостійної роботи (2 год.)

1. Опрацювання матеріалів лекції.

2. Опрацювання матеріалу на тему „Вираз скалярного, векторного, мішаного добутку через координати векторів в декартовій системі координат. ”

Література [1,3,10,13,19,22].


Практичне заняття 2. Скалярний добуток. Векторний добуток. Мішаний добуток.

1. Знаходження скалярного добутку векторів. Застосування скалярного добутку до обчислення довжини вектора, кута між векторами.
   
2. Обчислення векторного добутку векторів. Застосування векторного добутку до обчислення площі паралелограма.
   
3. Обчислення мішаного добутку векторів. Застосування мішаного добутку до дослідження орієнтації трійки векторів, дослідження, чи є вектори компланарними, до обчислення об’єму паралелепіпеда, піраміди.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [1,3,10,13,19,22].


ТЕМА 2. Диференціальне та інтегральне числення функцій однієї змінної (14 год.)


Лекція 3. Границя функції в точці, властивості границь. Означення похідної. Правила обчислення похідних.


Поняття границі функції в точці. Означення похідної. Правила обчислення похідних. Таблиця похідних елементарних функцій. Похідні старших порядків.


Завдання для самостійної роботи (2 год.)

1. Опрацювання матеріалів лекції.

2. Опрацювання матеріалу на тему „Доведення формул для похідних від елементарних функцій. ”

Література [4,7-8,11,16,18].


Практичне заняття 3. Техніка диференціювання.

1. Техніка диференціювання.
   
2. Похідні другого, третього порядків.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [4,7-8,11,16,18].


Лекція 4. Невизначений інтеграл. Техніка інтегрування. Поняття визначеного інтеграла. Зв’язок між невизначеним та визначеним інтегралами.


Поняття невизначеного інтеграла, його властивості. Таблиця невизначених інтегралів від елементарних функцій. Основні методи інтегрування: заміна змінної, інтегрування частинами. Поняття визначеного інтеграла. Зв’язок з невизначеним інтегралом: формула Ньютона-Лейбніца. Заміна змінних, інтегрування частинами у визначеному інтегралі.


Завдання для самостійної роботи (2 год.)

1. Опрацювання матеріалів лекції.

2. Опрацювання матеріалу на тему „Невласні інтеграли. Обчислення невласних інтегралів. ”

Література [4,7-8,11,16,18].


Практичне заняття 4. Невизначений інтеграл.

1. Обчислення невизначеного інтеграла функцій зведенням до табличних інтегралів.
   
2. Обчислення невизначених інтегралів за допомогою заміни змінних (лінійна заміна).
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [4,7-8,11,16,18].


Практичне заняття 5. Невизначений інтеграл (продовження).

1. Обчислення невизначених інтегралів за допомогою заміни змінних.
   
2. Обчислення невизначеного інтеграла за допомогою техніки інтегрування частинами.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [4,7-8,11,16,18].


Практичне заняття 6. Визначений інтеграл.

1. Обчислення визначеного інтеграла за допомогою формули Ньютона-Лейбніца.
   
2. Заміна змінних та інтегрування частинами у визначеному інтегралі.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

2.Підготовка до підсумкової модульної контрольної.

Література [4,7-8,11,16,18].


Практичне заняття 7. Підсумкова модульна контрольна.


ТИПОВЕ ЗАВДАННЯ МОДУЛЬНОЇ КОНТРОЛЬНОЇ РОБОТИ № 1


1. Задано вектори 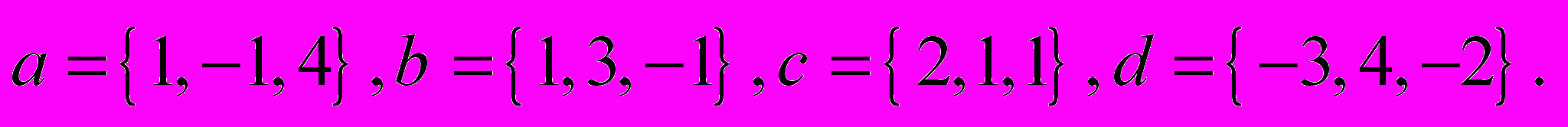Знайти

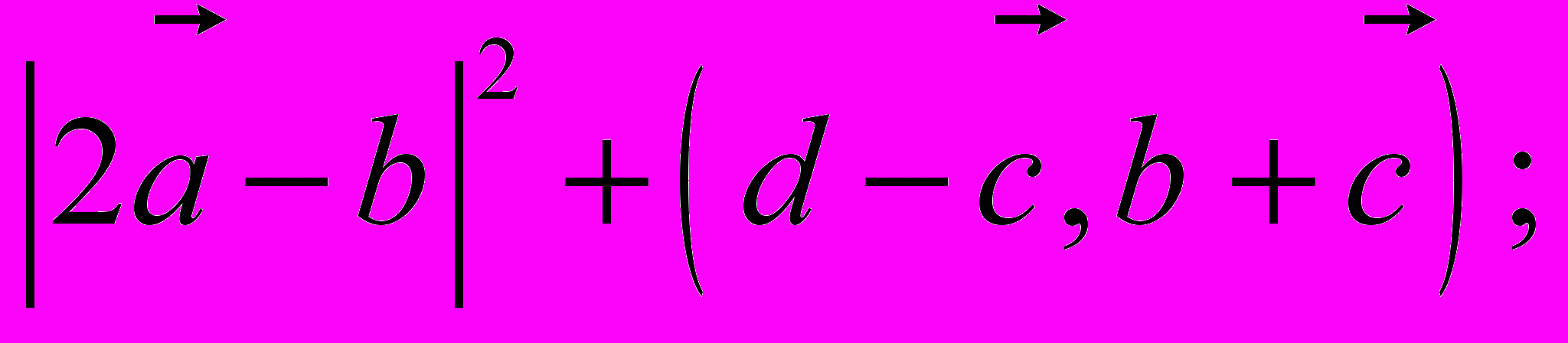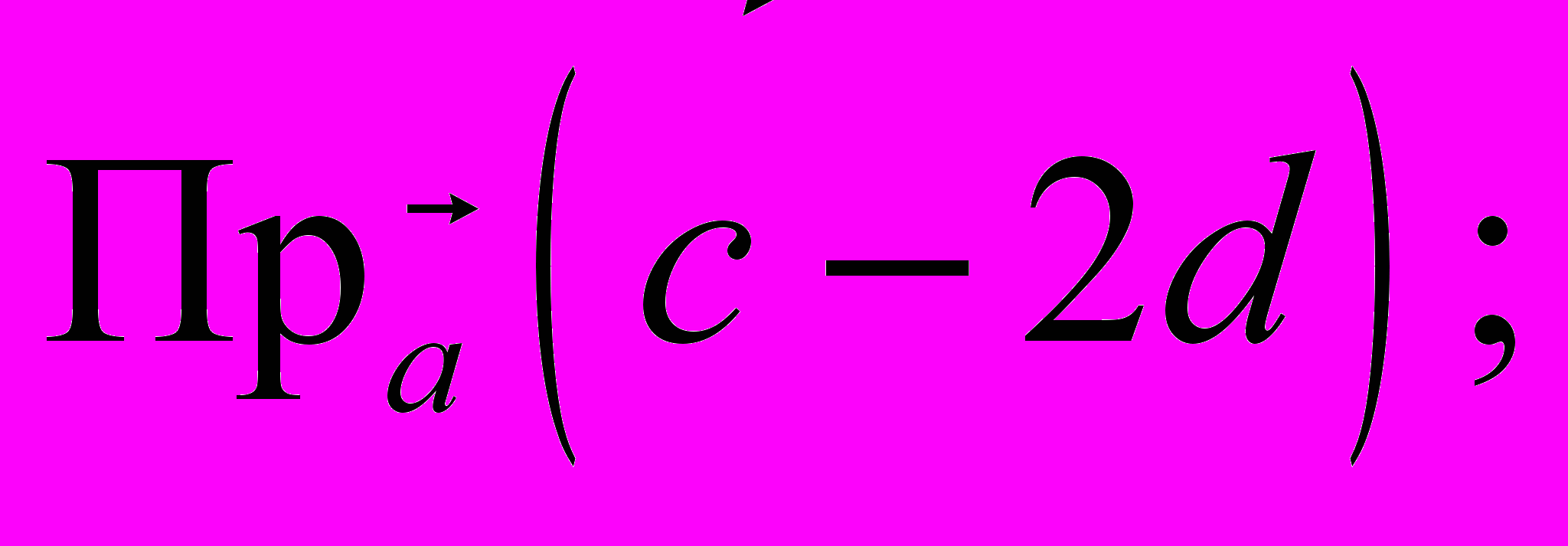а) б) в)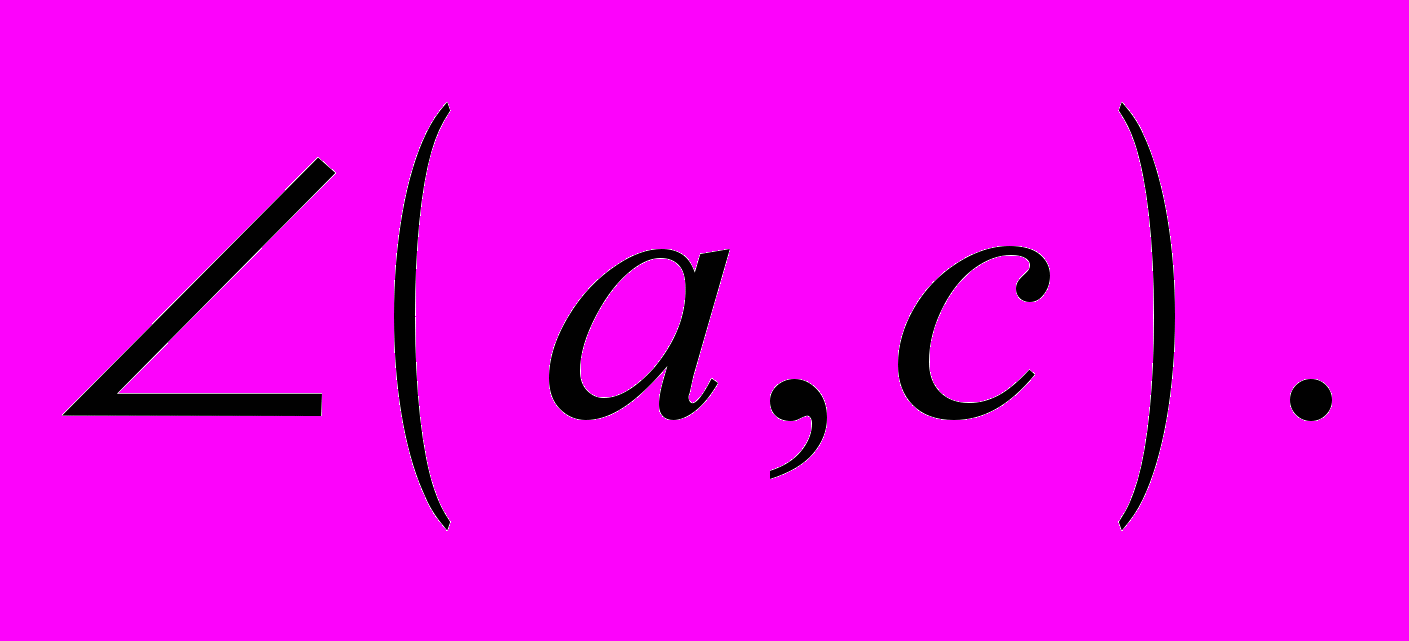

2. Задано вектори 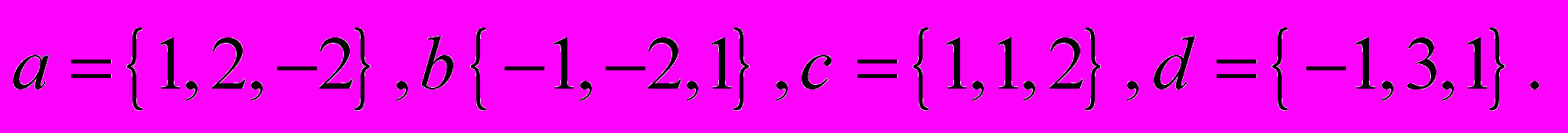Знайти .

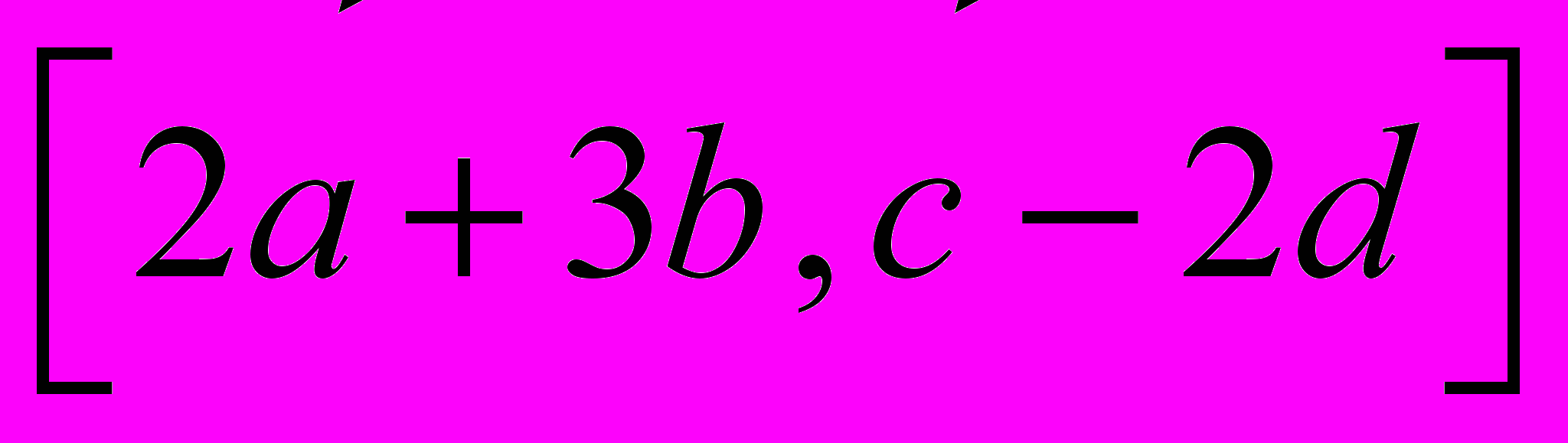3. Задано вектори 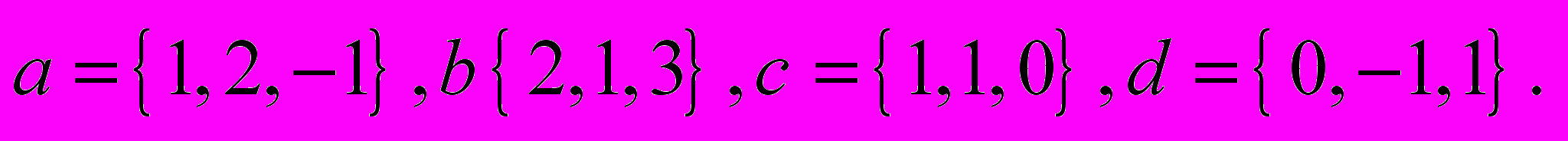Перевірити, чи будуть вектори 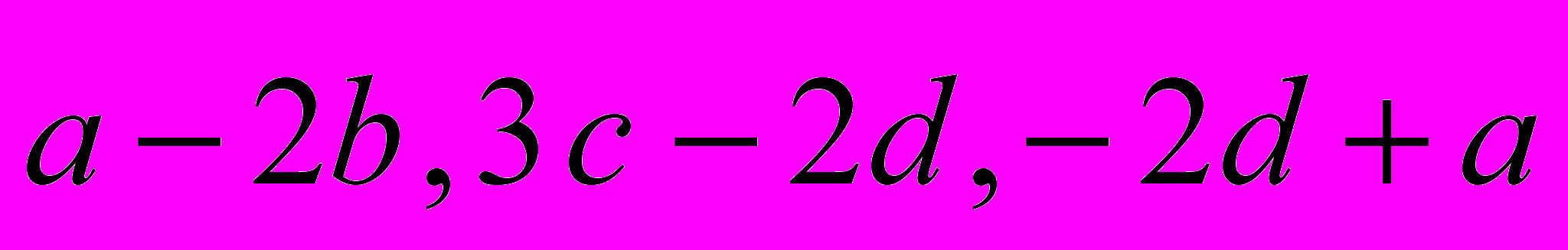компланарними.

4. Нехай 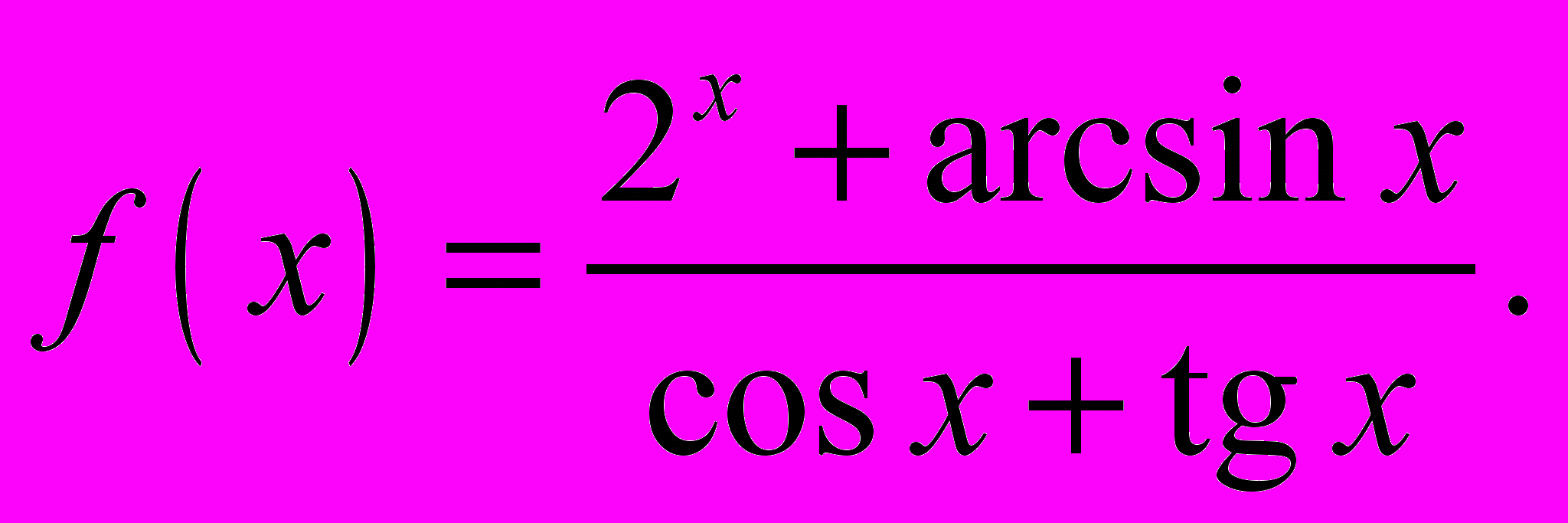Знайти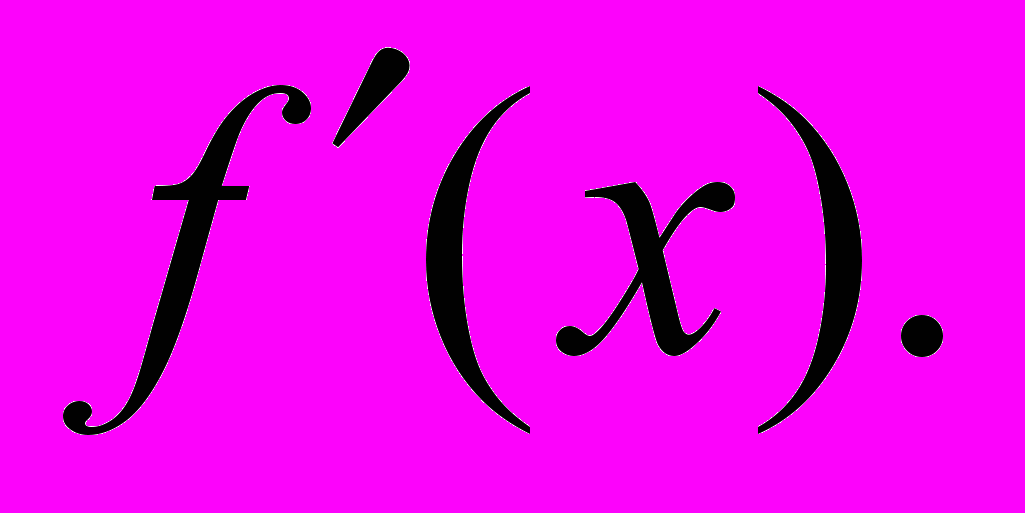

5. Нехай 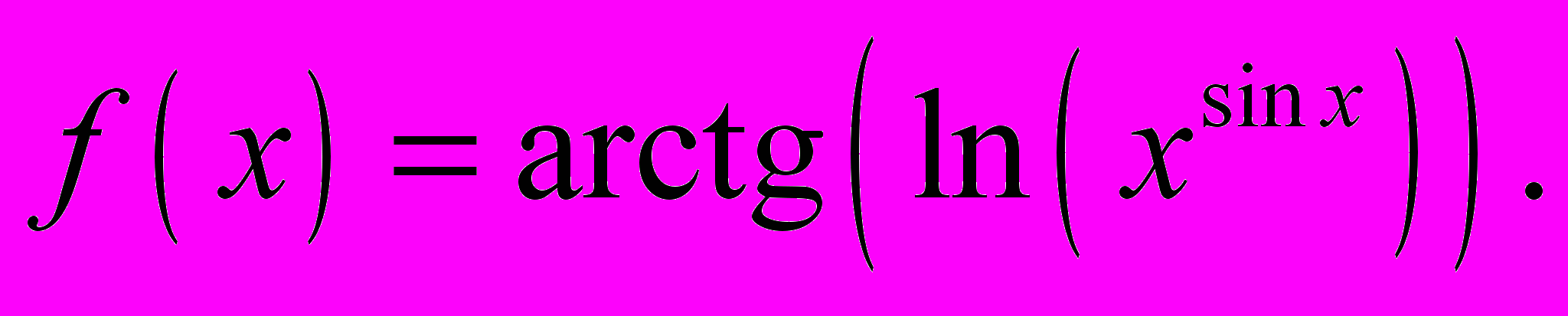Знайти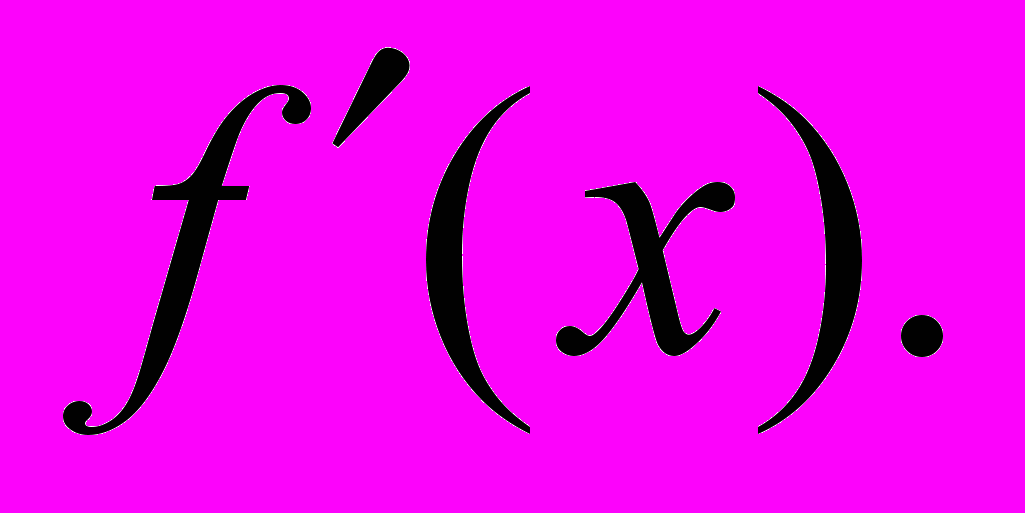

6. Знайти .

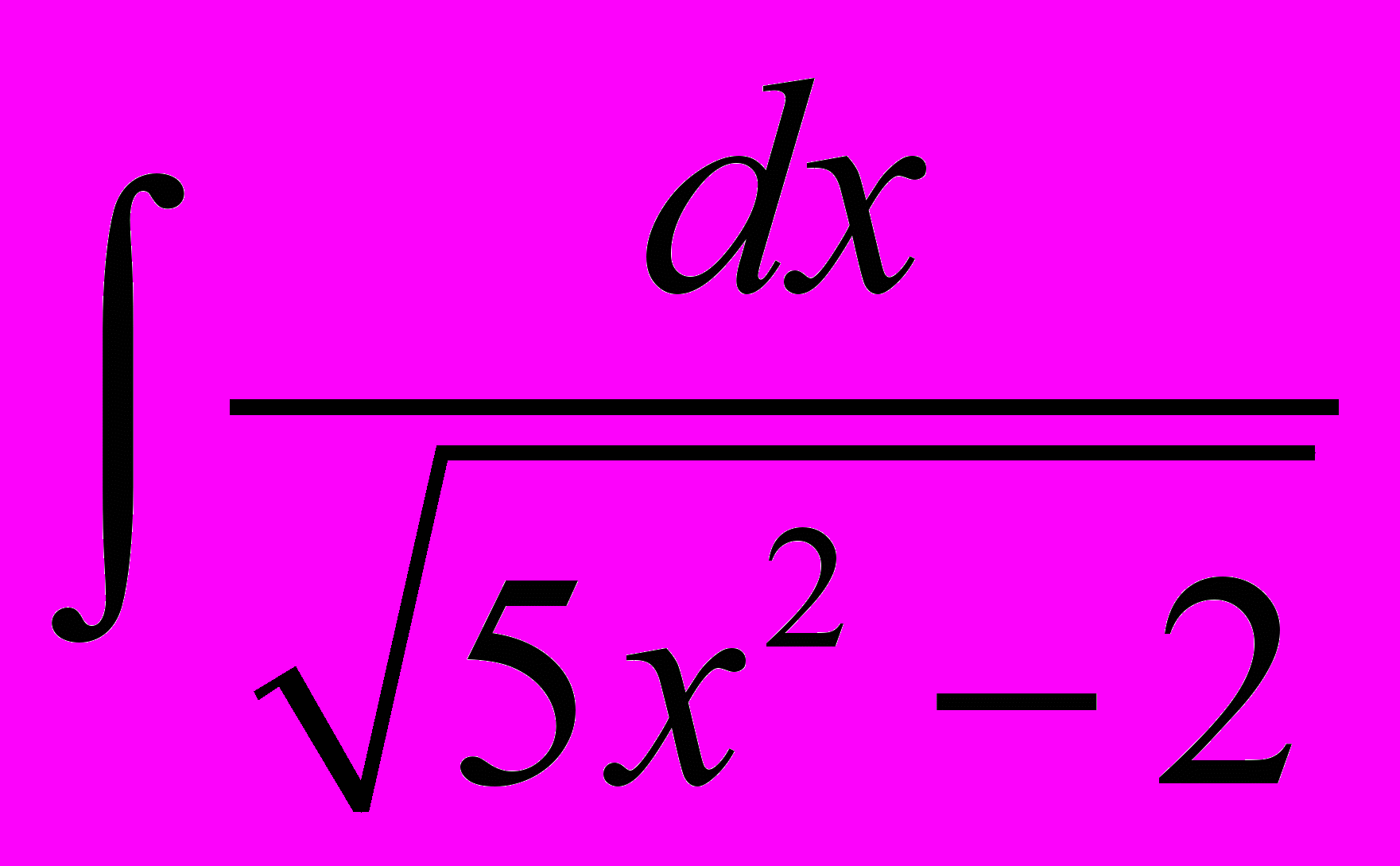7. Знайти .

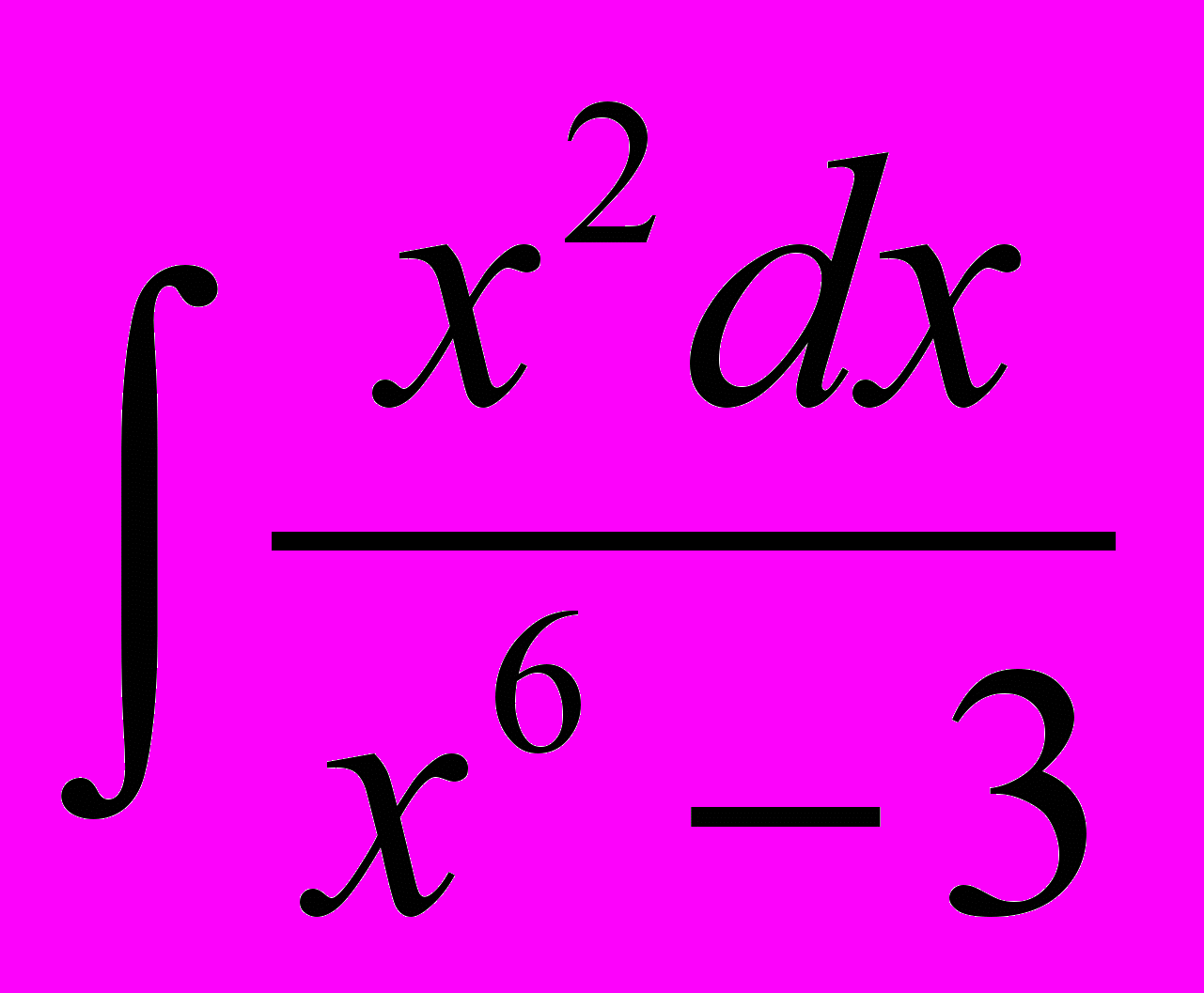8. Знайти .

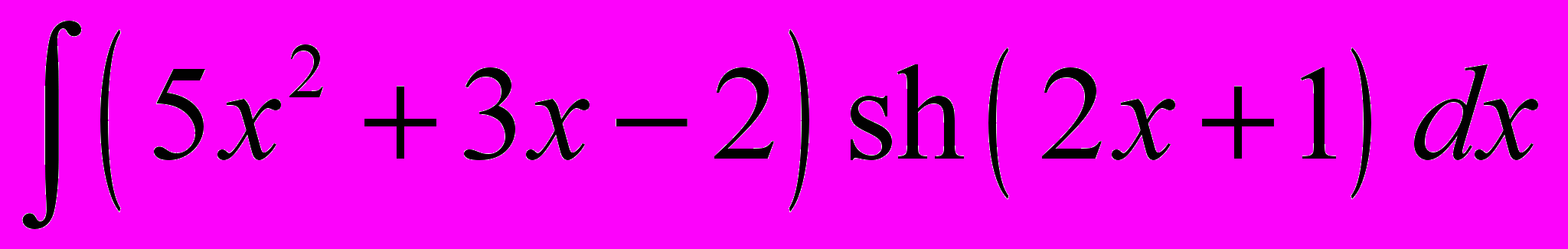9. Знайти .

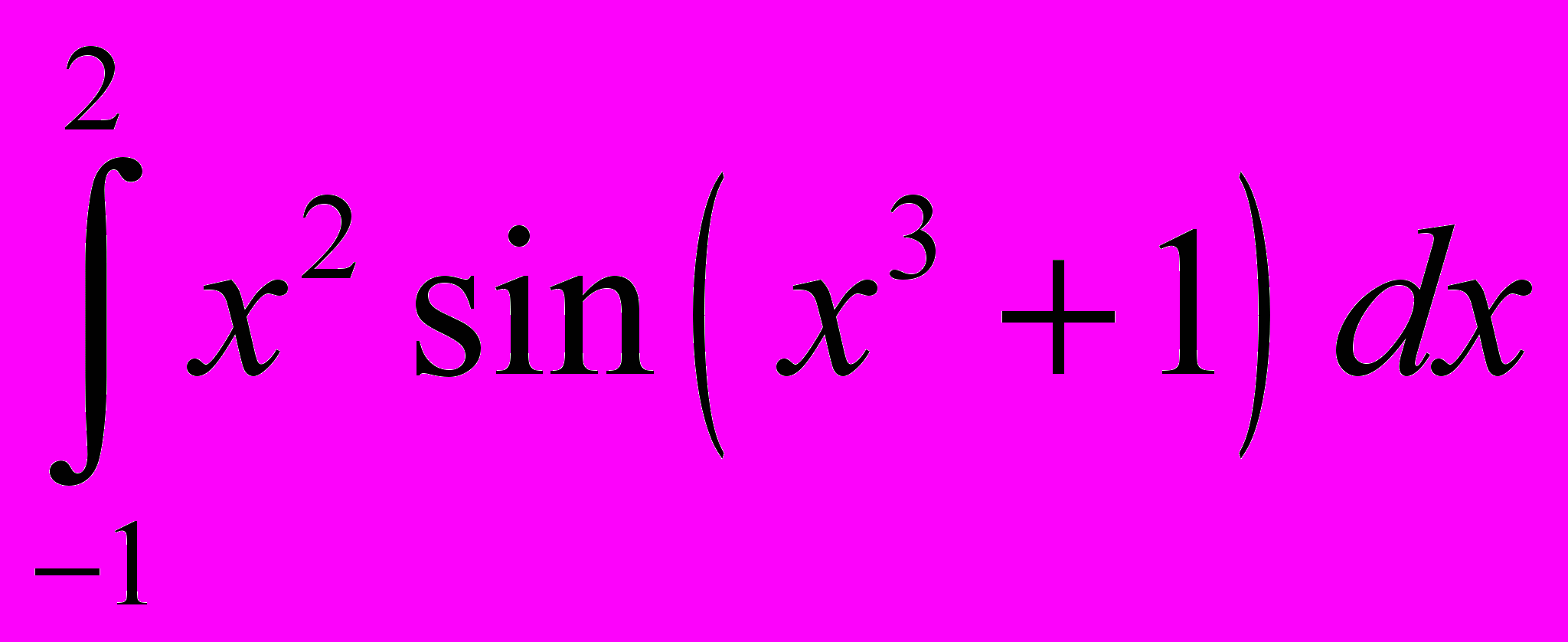10. Знайти .


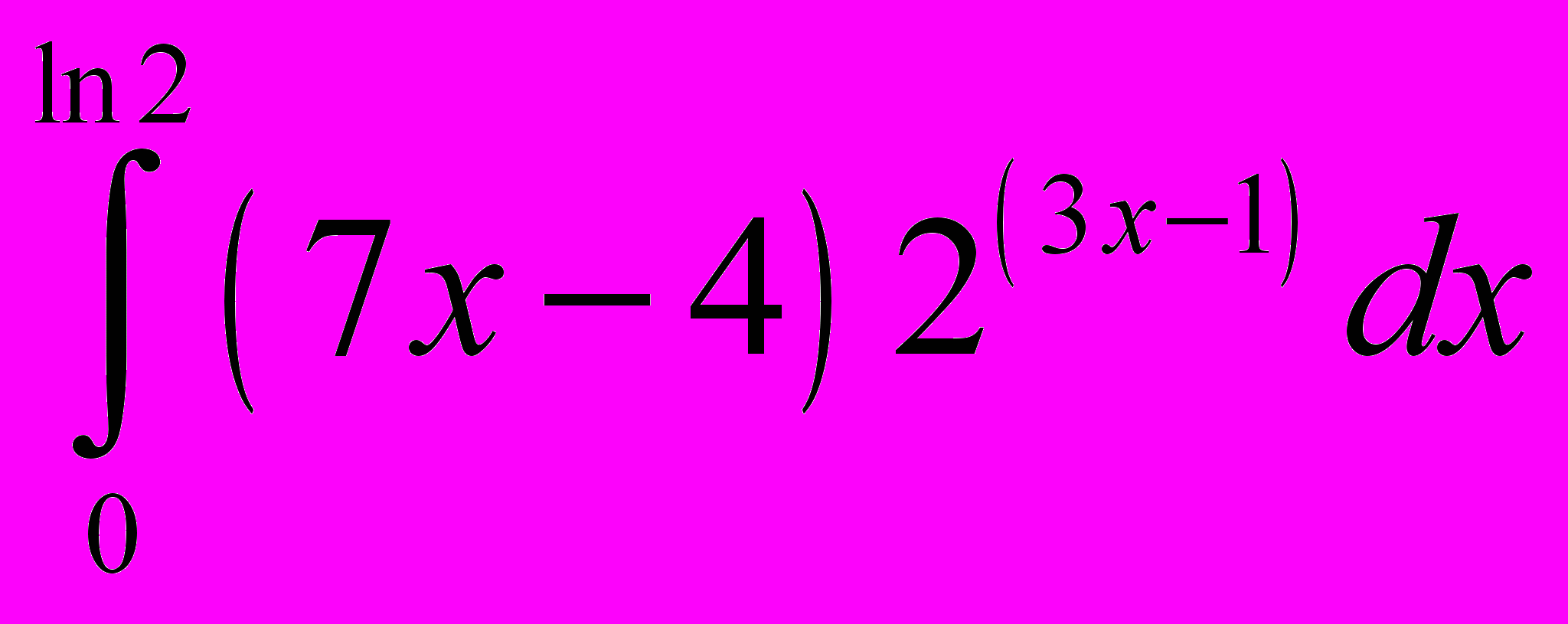Контрольні запитання до змістового модуля І

1. Означення визначника другого, третього порядків. Властивості визначників.
   
2. Означення вектора на прямій, на площині, в просторі. Лінійні операції над векторами, їх властивості.
   
3. Базис на прямій, на площині в просторі. Ортонормований базис. Координати вектора в базисі.
   
4. Означення скалярного добутку, його властивості. Вираз скалярного добутку через координати векторів. Геометричні властивості скалярного добутку.
   
5. Означення правої, лівої трійки векторів. Означення векторного добутку. Властивості векторного добутку. Вираз векторного добутку через координати векторів.
   
6. Означення мішаного добутку, його властивості. Вираз мішаного добутку через координати векторів.
   
7. Подвійний векторний добуток. Формули обчислення подвійного векторного добутку.
   
8. Поняття границі функції в точці.
   
9. Означення похідної. Похідні старших порядків.
   
10. Правила обчислення похідних.
    
11. Таблиця похідних елементарних функцій.
    
12. Поняття невизначеного інтеграла, його властивості.
    
13. Таблиця невизначених інтегралів від елементарних функцій.
    
14. Основні методи інтегрування: заміна змінної, інтегрування частинами.
    
15. Поняття визначеного інтеграла.
    
16. Зв’язок визначеного інтеграла з невизначеним: формула Ньютона-Лейбніца.
    
17. Заміна змінних, інтегрування частинами у визначеному інтегралі.
    

змістовий МОДУЛЬ ІІ.


ТЕМА 3. Застосування диференціального та інтегрального числення. (8 год.)


Лекція 5. Застосування теорії похідних. Поняття диференціала функції. Застосування визначеного інтеграла.


Фізичний та геометричний зміст похідної. Означення диференціала, його геометричний зміст. Формула малих приростів. Застосування похідних до дослідження властивостей функцій: монотонність, екстремуми функції, опуклість. Застосування визначеного інтеграла до обчислення площі фігур, довжини дуги кривої, об’єму тіл.


Завдання для самостійної роботи (2 год.)

1. Опрацювання матеріалів лекції.

2. Опрацювання матеріалу на тему „Застосування визначеного інтеграла для обчислення статичних моментів, моментів інерції, координат центру ваги. Формули для наближеного обчислення визначеного інтеграла. ”

Література [4,7-8,11,16,18].


Практичне заняття 8. Техніка диференціювання (продовження).

1. Знаходження диференціала функції.
   
2. Формула малих приростів.
   
3. Диференціювання функції, заданої параметрично, заданої неявно.
   
4. Геометричний зміст похідної.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [4,7-8,11,16,18].


Практичне заняття 9. Застосування похідних до дослідження функцій.

1. Застосування похідних до дослідження властивостей функцій: монотонність, екстремуми функції, опуклість.
   
2. Побудова графіків функцій.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [4,7-8,11,16,18].


Практичне заняття 10. Застосування визначеного інтеграла.

1. Застосування визначеного інтеграла до обчислення площі фігур, довжини дуги кривої, об’єму тіл.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [4,7-8,11,16,18].


ТЕМА 4. Спеціальні розділи вищої математики. (24 год.)


Лекція 6. Елементи теорії функцій багатьох змінних.


Поняття функції багатьох змінних. Поняття частинної похідної, похідної за напрямком. Диференціал функції багатьох змінних, його геометричний зміст. Формула малих приростів. Скалярні і векторні поля. Поняття градієнта скалярного поля, ротора та дивергенції векторного поля.


Завдання для самостійної роботи (2 год.)

1. Опрацювання матеріалів лекції.

2. Опрацювання матеріалу на тему „ Розклад функції багатьох змінних в степеневий ряд.”

Література [4,7-8,11,16,18].


Практичне заняття 11. Елементи теорії функцій багатьох змінних. Елементи теорії поля.

1. Поняття частинної похідної, похідної за напрямком.
   
2. Диференціал функції багатьох змінних. Формула малих приростів.
   
3. Скалярні поля. Градієнт скалярного поля.
   
4. Векторні поля. Ротор та дивергенція векторного поля.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [4,7-8,11,16,18].


Практичне заняття 12. Елементи теорії функцій комплексної змінної.

1. Арифметичні дії над комплексними числами. Геометрична інтерпретація комплексних чисел.
   
2. Модуль та аргумент комплексного числа. Тригонометрична та показникові форми запису комплексних чисел.
   
3. Формула Муавра. Корінь з комплексного числа.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [6,9,14].


Лекція 7. Елементи теорії рядів. Степеневі ряди. Ряди Фур’є.


Поняття ряду, збіжності ряду. Степеневі ряди, область збіжності степеневого ряду. Розклад функції в степеневий ряд. Стандартні розклади. Тригонометричний ряд Фур’є.


Завдання для самостійної роботи (2 год.)

1. Опрацювання матеріалів лекції.

2. Опрацювання матеріалу на тему „Формула Стірлінга. Перетворення Фур’є. ”

Література [4,7-8,11,16,18].


Практичне заняття 13. Степеневі ряди.

1. Радіус збіжності степеневого ряду.
   
2. Розклад функції в степеневий ряд.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [4,7-8,11,16,18].


Практичне заняття 14. Ряди Фур’є.

1. Розклад функції в ряд Фур’є.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [4,7-8,11,16,18].


Лекція 8. Елементи теорії диференціальних рівнянь.


Поняття диференціального рівняння. Методи розв’язання деяких типів диференціальних рівнянь: рівнянь з відокремлюваними змінними, лінійних рівнянь, лінійних рівнянь зі сталими коефіцієнтами другого порядку.


Завдання для самостійної роботи (2 год.)

1. Опрацювання матеріалів лекції.

2. Опрацювання матеріалу на тему „Методи розв’язання лінійних неоднорідних рівнянь зі сталими коефіцієнтами другого порядку. ”

Література [5,12,15,20-21].


Практичне заняття 15. Елементи теорії диференціальних рівнянь.

1. Рівняння з відокремлюваними змінними.
   
2. Лінійні рівняння першого порядку.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [5,12,15,20-21].


Практичне заняття 16. Елементи теорії диференціальних рівнянь (продовження).

1. Лінійні рівняння зі сталими коефіцієнтами другого порядку.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

Література [5,12,15,20-21].


Лекція 9. Елементи комбінаторики.


Задача комбінаторики. Основний принцип комбінаторики: правило множення. Впорядковані множини, перестановки. Розміщення, комбінації з n по k. Перестановки, комбінації з повтореннями. Моделі Максвелла-Больцмана, Бозе-Ейнштейна, Фермі-Дірака.


Завдання для самостійної роботи (2 год.)

1. Опрацювання матеріалів лекції.

2. Опрацювання матеріалу на тему „Класичне означення ймовірності. ”

Література [2,17].


Практичне заняття 17. Елементи комбінаторики.

1. Задачі про число перестановок множини, яка складається з n елементів.
   
2. Задачі про число розміщень по k елементів множини, яка складається з n елементів.
   
3. Задачі про число комбінацій по k елементів множини, яка складається з n елементів.
   
4. Задачі про перестановки, комбінації з повтореннями.
   

Завдання для самостійної роботи (2 год.)

1. Робота над практичним завданням.

2.Підготовка до підсумкової модульної контрольної.

Література [2,17].


Практичне заняття 18. (2 години) Підсумкова модульна контрольна.


ТИПОВЕ ЗАВДАННЯ МОДУЛЬНОЇ КОНТРОЛЬНОЇ РОБОТИ № 2


1. Знайти 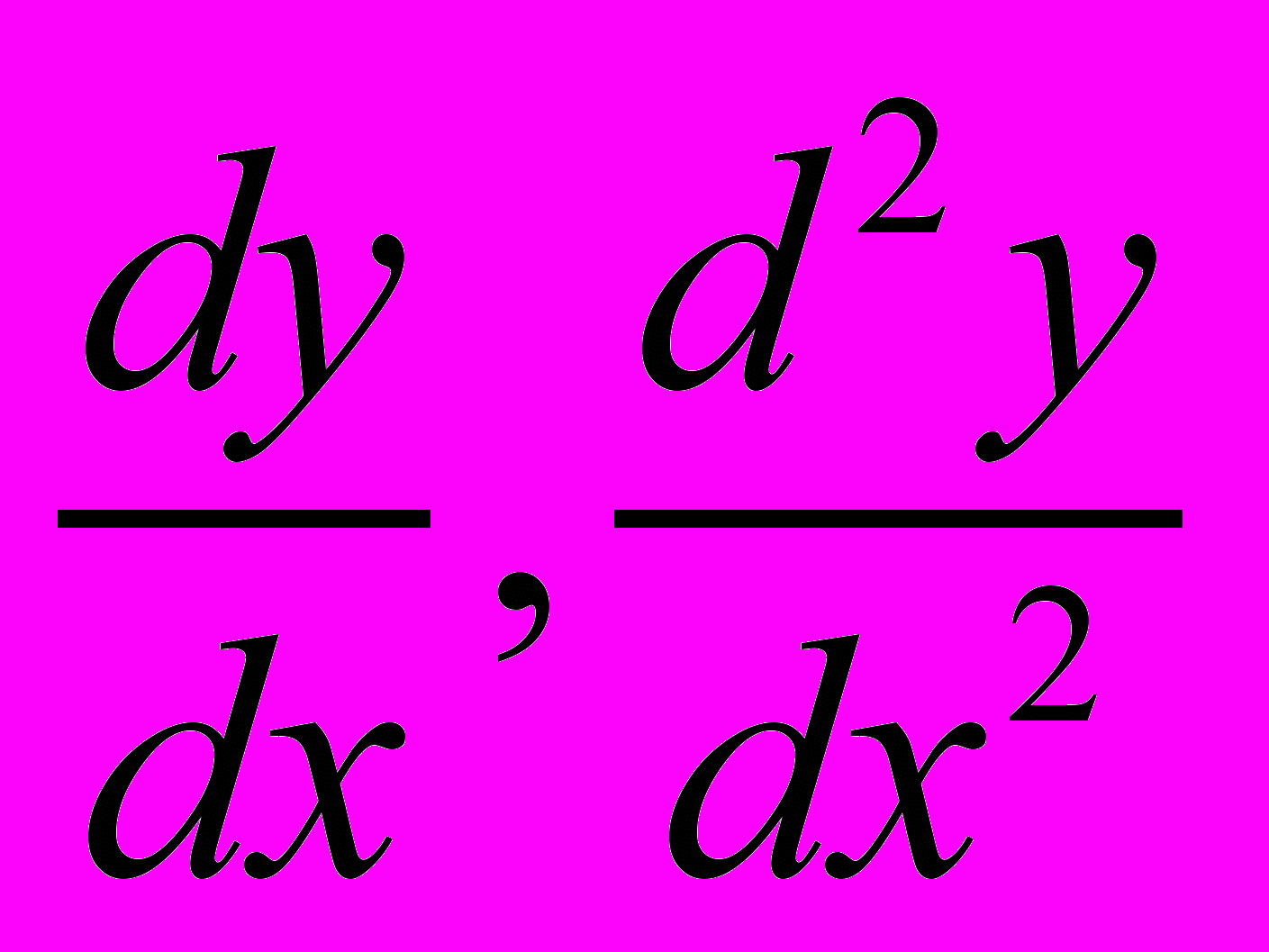, якщо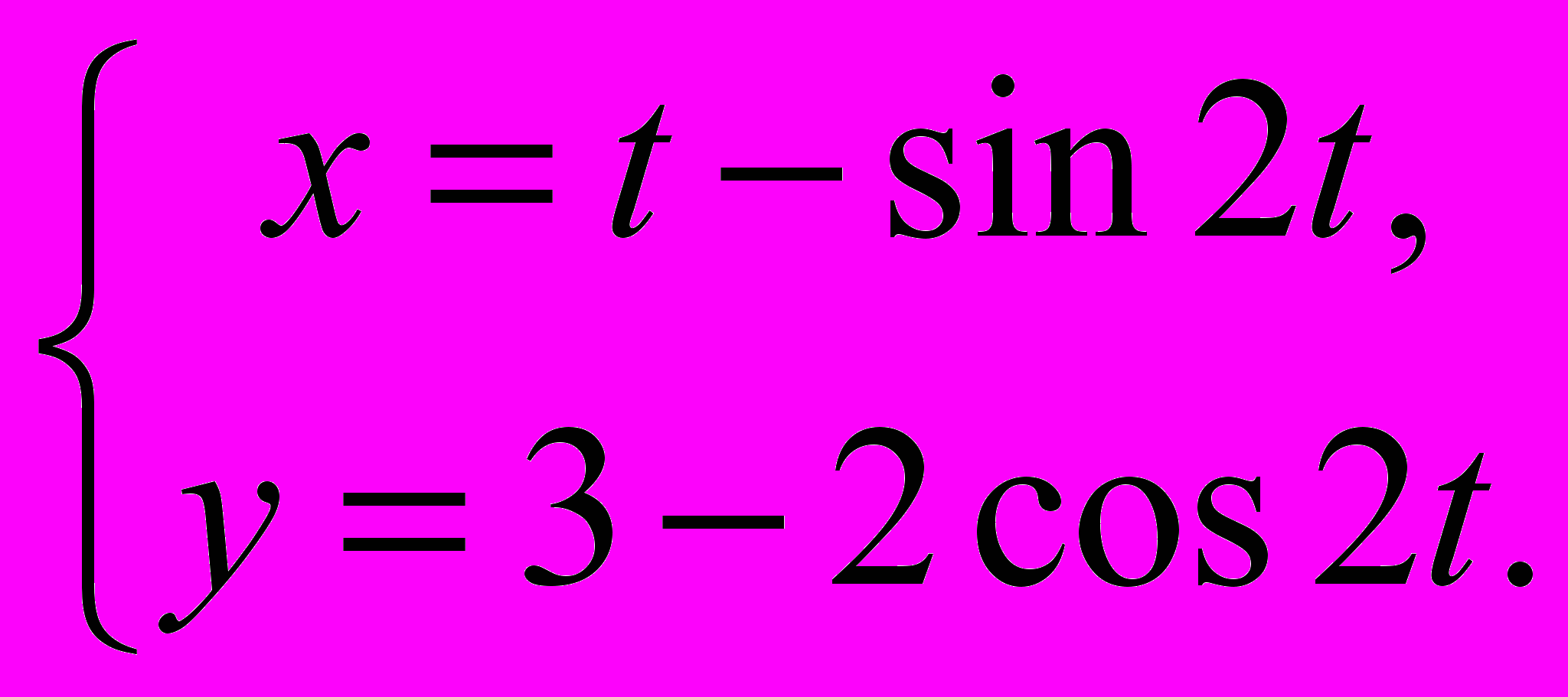

2. Дослідити функцію 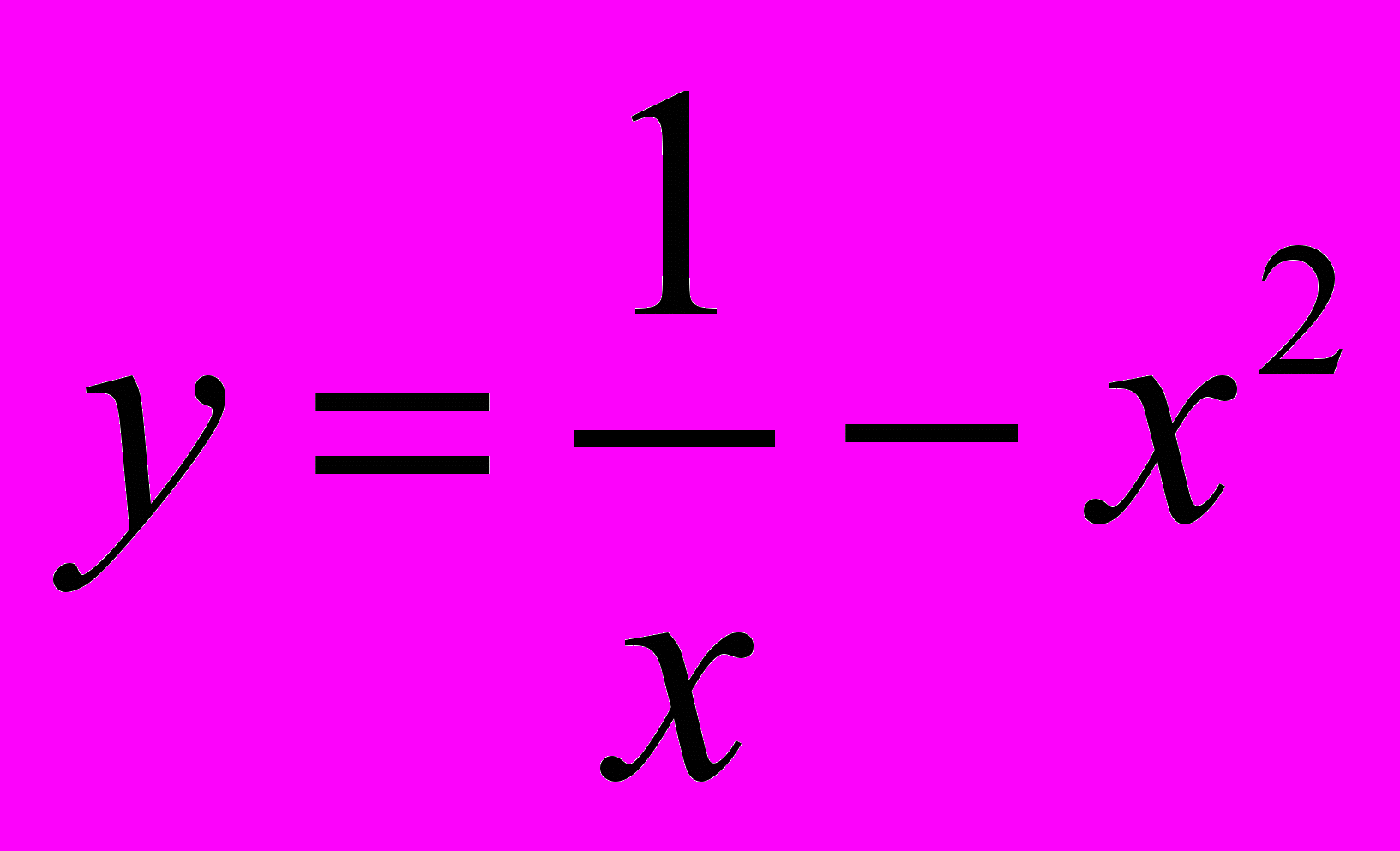та побудувати її графік.


3. Знайти площу, яка обмежена кривими .

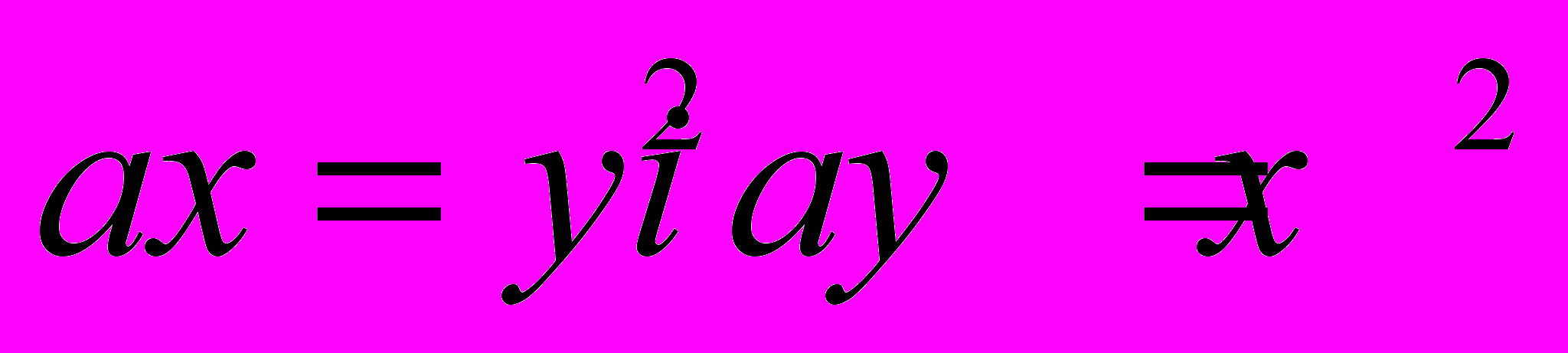4. Розкласти функцію в степеневий ряд і вказати радіус збіжності отриманого ряду.

5. Розкласти функцію 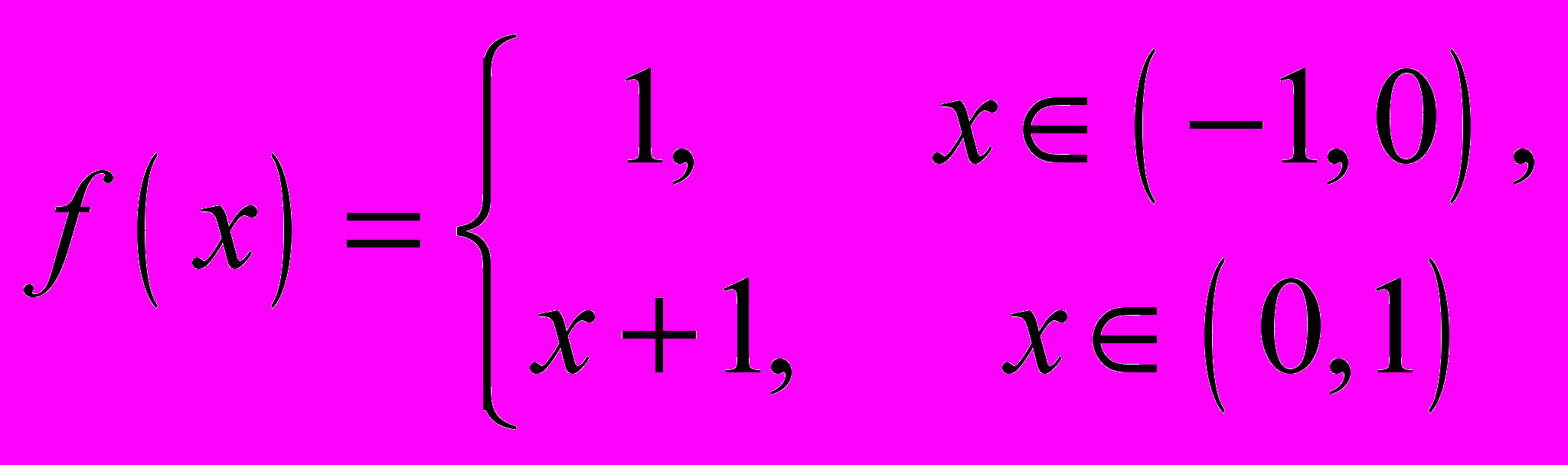в ряд Фур’є.

6. Нехай 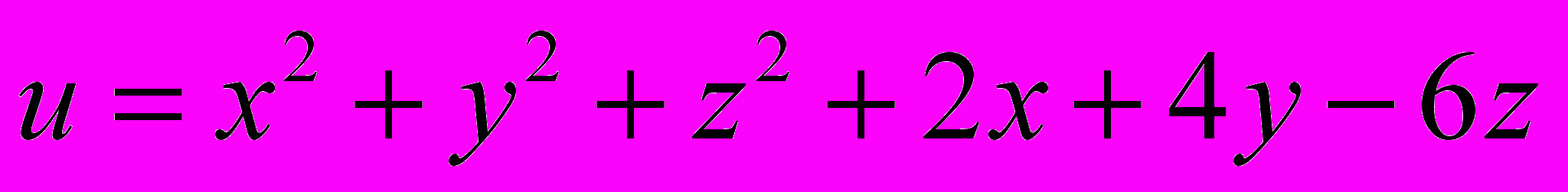. Знайт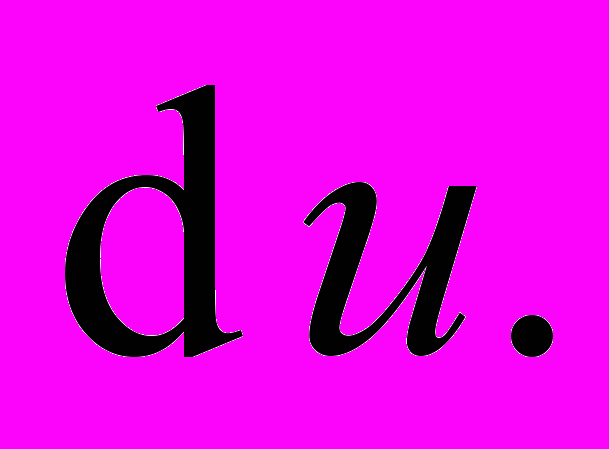и Нехай 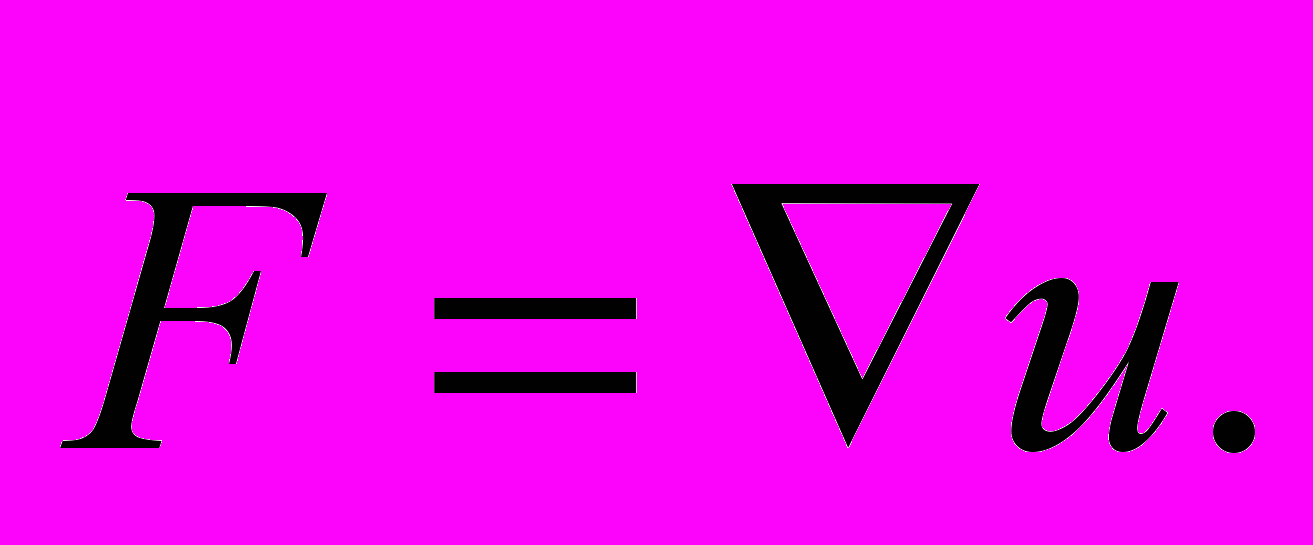Знайти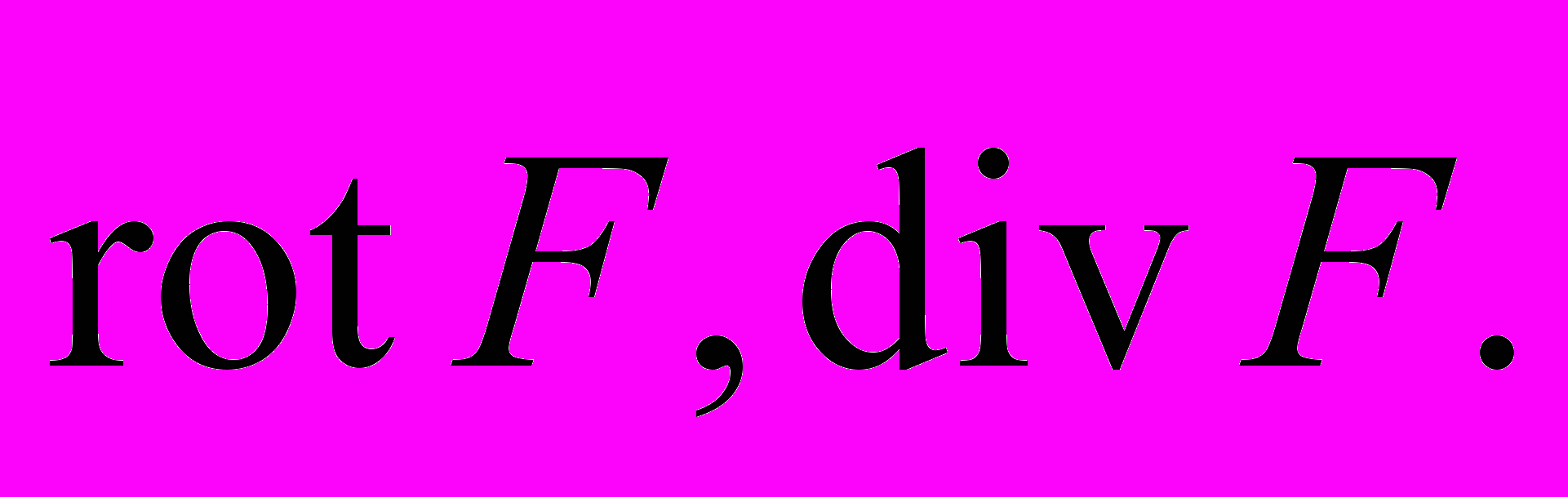

7. Нехай 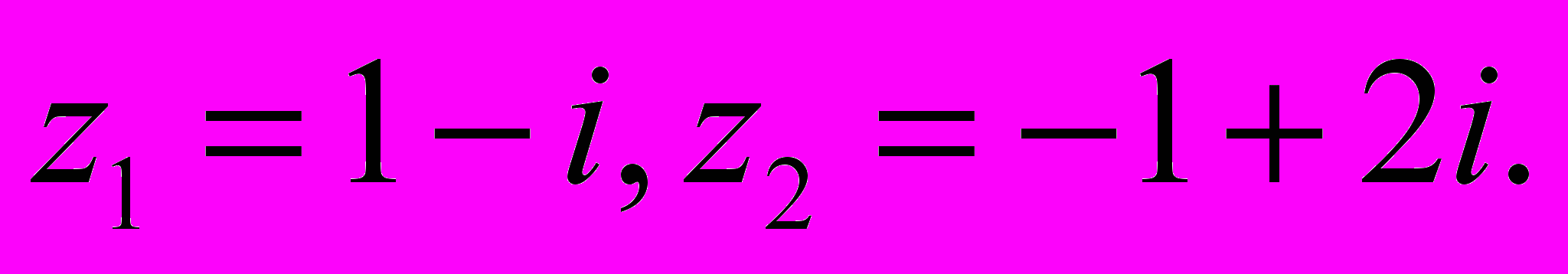Знайти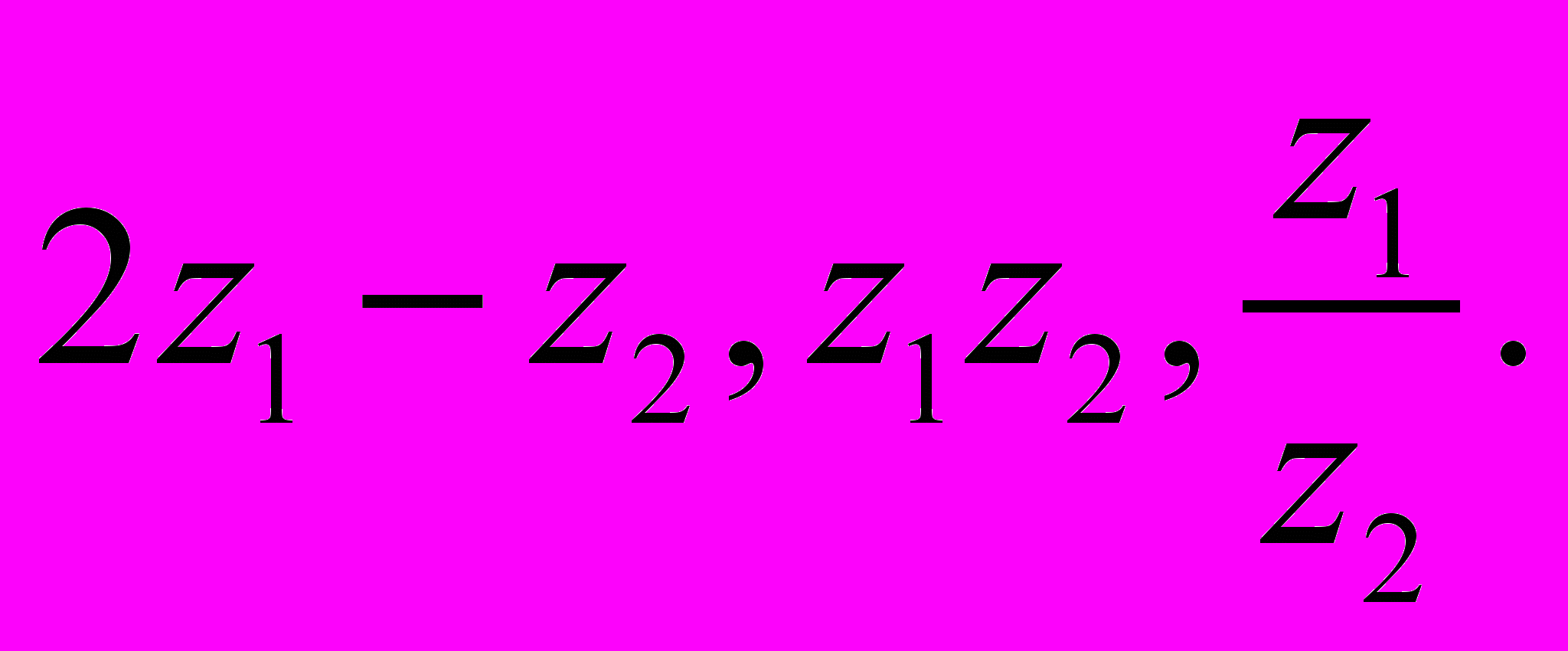Записати числа 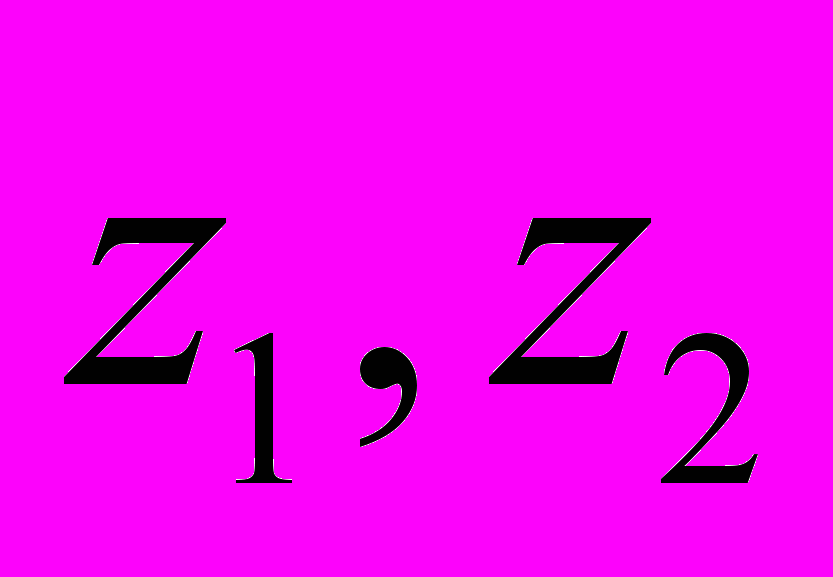в показниковій формі.

8. Розв’язати рівняння

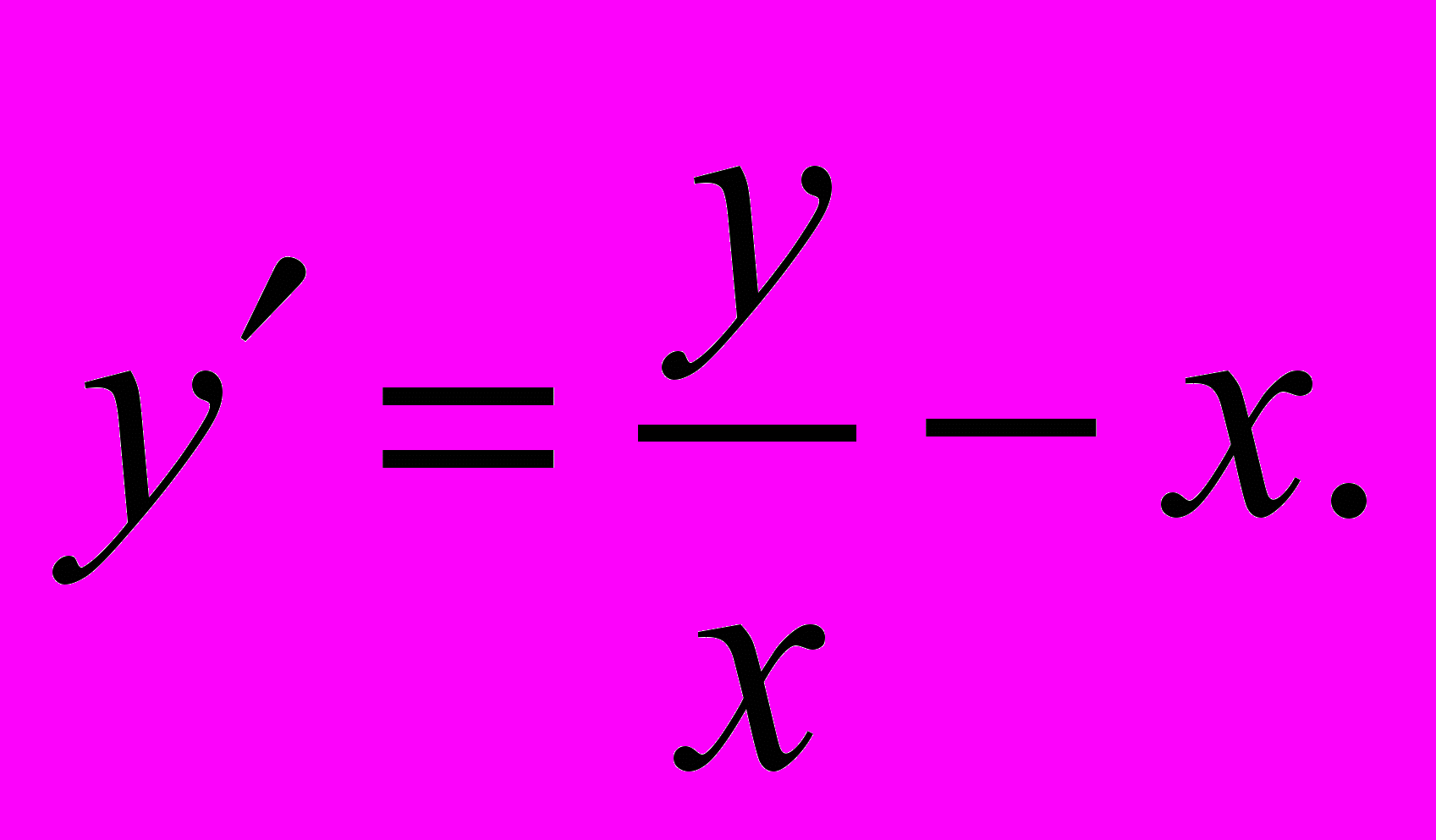
9. Розв’язати рівняння

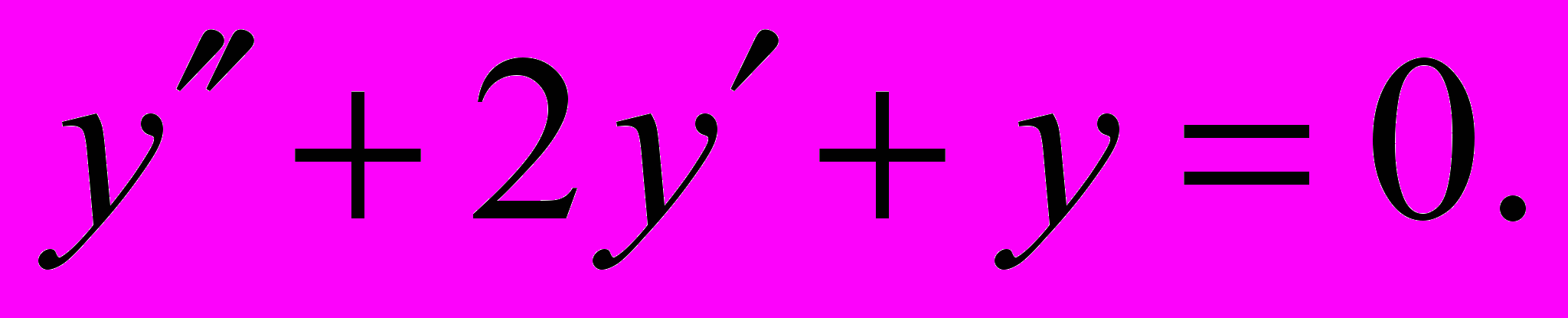
10. На полиці стоїть m книжок в чорних обкладинках і n книжок в блакитних обкладинках, причому всі книжки різні. Скількома способами можна розставити всі книжки так, щоб книжки в чорних обкладинках стояли поруч?


Контрольні запитання до змістового модуля ІІ

1. Фізичний та геометричний зміст похідної.
   
2. Означення диференціала, його геометричний зміст.
   
3. Формула малих приростів.
   
4. Застосування похідних до дослідження властивостей функцій: монотонність, екстремуми функції, опуклість.
   
5. Застосування визначеного інтеграла до обчислення площі фігур, довжини дуги кривої, об’єму тіл.
   
6. Поняття ряду, збіжності ряду.
   
7. Степеневі ряди, область збіжності степеневого ряду.
   
8. Розклад функції в степеневий ряд. Стандартні розклади.
   
9. Тригонометричний ряд Фур’є.
   
10. Поняття функції багатьох змінних. Поняття частинної похідної, похідної за напрямком.
    
11. Диференціал функції багатьох змінних, його геометричний зміст.
    
12. Формула малих приростів.
    
13. Скалярні і векторні поля. Поняття градієнта скалярного поля, ротора та дивергенції векторного поля.
    
14. Поняття диференціального рівняння.
    
15. Методи розв’язання рівнянь з відокремлюваними змінними.
    
16. Методи розв’язання лінійних рівнянь.
    
17. Методи розв’язання лінійних рівнянь зі сталими коефіцієнтами другого порядку.
    
18. Основний принцип комбінаторики: правило множення.
    
19. Впорядковані множини, перестановки.
    
20. Розміщення, комбінації з n по k.
    
21. Перестановки, комбінації з повтореннями.
    
22. Моделі Максвелла-Больцмана, Бозе-Ейнштейна, Фермі-Дірака.
    

Перелік запитань на іспит

1. Означення визначника другого, третього порядків. Властивості визначників.
   
2. Означення вектора на прямій, на площині, в просторі. Лінійні операції над векторами, їх властивості.
   
3. Базис на прямій, на площині в просторі. Ортонормований базис. Координати вектора в базисі.
   
4. Означення скалярного добутку, його властивості. Вираз скалярного добутку через координати векторів. Геометричні властивості скалярного добутку.
   
5. Означення правої, лівої трійки векторів. Означення векторного добутку. Властивості векторного добутку. Вираз векторного добутку через координати векторів.
   
6. Означення мішаного добутку, його властивості. Вираз мішаного добутку через координати векторів.
   
7. Подвійний векторний добуток. Формули обчислення подвійного векторного добутку.
   
8. Означення похідної. Похідні старших порядків. Правила обчислення похідних.
   
9. Таблиця похідних елементарних функцій.
   
10. Поняття невизначеного інтеграла, його властивості.
    
11. Таблиця невизначених інтегралів від елементарних функцій.
    
12. Основні методи інтегрування: заміна змінної, інтегрування частинами.
    
13. Поняття визначеного інтеграла. Зв’язок визначеного інтеграла з невизначеним: формула Ньютона-Лейбніца.
    
14. Заміна змінних, інтегрування частинами у визначеному інтегралі.
    
15. Фізичний та геометричний зміст похідної.
    
16. Означення диференціала, його геометричний зміст. Формула малих приростів.
    
17. Застосування похідних до дослідження властивостей функцій: монотонність, екстремуми функції, опуклість.
    
18. Застосування визначеного інтеграла до обчислення площі фігур, довжини дуги кривої, об’єму тіл.
    
19. Поняття ряду, збіжності ряду. Степеневі ряди, область збіжності степеневого ряду.
    
20. Розклад функції в степеневий ряд. Стандартні розклади.
    
21. Тригонометричний ряд Фур’є.
    
22. Поняття функції багатьох змінних. Поняття частинної похідної, похідної за напрямком.
    
23. Диференціал функції багатьох змінних, його геометричний зміст. Формула малих приростів.
    
24. Скалярні і векторні поля. Поняття градієнта скалярного поля, ротора та дивергенції векторного поля.
    
25. Поняття диференціального рівняння.
    
26. Методи розв’язання рівнянь з відокремлюваними змінними.
    
27. Методи розв’язання лінійних рівнянь.
    
28. Методи розв’язання лінійних рівнянь зі сталими коефіцієнтами другого порядку.
    
29. Основний принцип комбінаторики: правило множення.
    
30. Впорядковані множини, перестановки.
    
31. Розміщення, комбінації з n по k.
    
32. Перестановки, комбінації з повтореннями.
    
33. Моделі Максвелла-Больцмана, Бозе-Ейнштейна, Фермі-Дірака.
    

СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

а) основна:

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры.  М.: Наука., 1987.  320 с.
   
2. Гихман И.И., Скороход А.В., Ядренко М.И. Теория вероятностей и математическая статистика. – К.: Вища школа., 1988. – 439 с.
   
3. Ильин В.А.,Позняк Э.Г. Аналитическая геометрия. М.: Наука., 1971. 232 с.
   
4. Ильин В.А., Позняк Е.Г. Основы математического анализа, М., 1972.
   
5. Кривошея С.А., Перестюк М.О., Бурим В.М. Диференціальні та інтегральні рівняння. – К.: Либідь., 2004. – 408 с.
   
6. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука., 1987. 688 с.
   
7. Ляшко И.И., Боярчук О.К., Гай Я.Г., Калайда О.Ф., Математический анализ, К., 1985.
   

б) додаткова:

8. Дороговцев А.Я., Математический анализ. – К.: Вища школа., 1985. –528 с.
   
9. Єфіменко СВ., Кривошея С.А., Придатченко Ю.В., Янішевський А.Т., Комплексні числа. – К. РВЦ КУ, 1997.
   
10. Ефимов Н.В. Краткий курс аналитической геометрии.  М.: Наука., 1975.  272 с.
    
11. Ляшко И.И., Боярчук О.К., Гай Я.Г., Голавач Г.П., Математический анализ в примерах и задачах. – К., 1978-1986.
    
12. Самойленко А.М., Кривошея С.А., Перестюк М.О. Диференціальні рівняння в прикладах і задачах. – К.: Вища школа., 1994. – 455 с.
    

в) збірники задач:

13. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре.  М.: Наука., 1987.  496 с.
    
14. Волковыский Л.И., Лунц Г.Л., Араманович И.Г. Сборник задач по теории функций комплексного переменного.  М.: Наука., 1970.  320 с.
    
15. Головач Г.П., Калайда О.Ф. Збірник задач з диференціальних та інтегральних рівнянь. – К.: Техніка., 1997. – 288 с.
    
16. Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: Наука, 1972. – 542 с.
    
17. Дороговцев А.Я., Сильвестров Д.С., Скороход А.В., Ядренко М.И. Теория вероятностей. – К.: Вища школа., 1980. – 432 с.
    
18. Єфіменко СВ., Кривошея С.А. Контрольні завдання з математичного аналізу. –К.: ВПЦ КУ, 2002. ­– 68 с.
    
19. Клетеник Д.В. Сборник задач по аналитической геометрии.  М.: Наука., 1972.  240 с.
    
20. Романенко В.К. Сборник задач по дифференциальным уравнениям и вариационному исчислению.  М.: ЮНИМЕДИАСТАЙЛ., 2002.  256 с.
    
21. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям.  М.: Наука., 1992.  128 с.
    
22. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии.  М.: Наука., 1970.  336 с.