Geum.ru

Робоча навчальна програма для студентів спеціальності 070201 «Радіофізика І електроніка» Затверджено

Вид материалаДокументы

Содержание


Семінар № 1. Комплексні числа
Рекомендована література
Семінар № 2. Елементарні функції комплексної змінної
Рекомендована література
Завдання для самостійної роботи
Лекція № 3. Аналітичні функції
Семінар № 4. Умови Коші–Рімана
Завдання для самостійної роботи
Семінар № 6. Інтегральна формула Коші
Рекомендована література
Модульна контрольна робота № 1 (2 год).
Семінар № 7 Ряд Лорана
Рекомендована література
Семінар № 7. Особливі точки
Рекомендована література
Семінар № 8. Обчислення лишків
Рекомендована література
Семінар № 10. Обчислення невласних інтегралів
Тема № 10. «Плоскі векторні поля і фізичний зміст аналітичної функції»
Лекція № 9. Фізичний зміст аналітичної функції
...
Полное содержание
Подобный материал:
1   2   3
Тема № 1. «Комплексні числа»


Лекція № 1. Комплексні числа (2 год).

Означення комплексних чисел. Операції над комплексними числами. Способи зображення комплексних чисел: векторне зображення, матричне зображення. Алгебраїчна замкненість поля комплексних чисел. Добування кореня з комплексного числа. Основна теорема алгебри. Невпорядкованість комплексних чисел. Послідовності комплексних чисел. Граничні точки. Нескінченно віддалена точка та компактифікація поля комплексних чисел. Стереографічна проекція. Сфера Рімана.


Семінар № 1. Комплексні числа (2 год).

Комплексні числа. Операції над комплексними числами. Способи зображення комплексних чисел.


Завдання для самостійної роботи: (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Тема № 2. «Функції комплексної змінної»


Лекція № 2. Функції комплексної змінної (2 год).

Неперервні функції. Однозначні, багатозначні, багатолистні функції. Інтеграл від функції комплексної змінної. Похідна функції комплексної змінної. Формальні похідні Коші. Аналітична функція. Умови Коші–Рімана в декартових, полярних і довільних ортогональних координатах.


Семінар № 2. Елементарні функції комплексної змінної (2 год).

Вивчення властивостей основних елементарних функції комплексної змінної.


Завдання для самостійної роботи (6 год).

Вивчення матеріалів лекції, вивчення елементарних функцій комплексної змінної та їх властивостей за рекомендованою літературою, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Тема № 3. «Інтеграл від функції комплексної змінної»


Семінар № 3. Інтеграл від функції комплексної змінної (1 год).

Інтеграл від функції комплексної змінної, його властивості. Обчислення інтегралу від елементарних функцій комплексної змінної.


Завдання для самостійної роботи (2 год).

Опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Тема № 4. «Аналітичні функції»


Лекція № 3. Аналітичні функції (2 год).

Означення та основні властивості аналітичних функцій. Геометрична інтерпретація аналітичної функції. Зміст модуля та аргументна похідної. Поняття конформного відображення


Семінар № 4. Умови Коші–Рімана (2 год).

Умови Коші–Рімана. Геометричний зміст аналітичності.


Семінар № 5. Гармонічні функції (1 год).

Знаходження аналітичної функції за її дійсною чи уявною частинами, або за її модулем чи аргументом.


Завдання для самостійної роботи (6 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Тема № 5. «Інтеграл від аналітичної функції»


Лекція № 4. Інтеграл від аналітичної функції (2 год).

Інтеграл від аналітичної функції в однозв'язній та багатозв'язній області. Інтегральна формула Коші. Теорема про середнє значення. Теорема про максимум модуля. Формула Коші для похідної аналітичної функції. Оцінки модуля похідної аналітичної функції. Нескінченна диференційовність аналітичної функції. Три означення аналітичної функції. Теорема Ліувілля. Теорема Морера.


Семінар № 6. Інтегральна формула Коші (2 год).

Обчислення контурних інтегралів за допомогою інтегральної формули Коші.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Контрольні запитання

  1. Комплексні числа. Означення, модуль та аргумент комплексного числа. Зображення комплексних чисел. Тригонометрична та показникова форми комплексного числа. Приклад.
  2. Основні операції над комплексними числами та поле комплексних чисел. Алгебраїчна замкненість поля комплексних чисел.
  3. Невпорядкованість комплексних чисел.
  4. Послідовності комплексних чисел. Граничні точки.
  5. Нескінченно віддалена точка та компактифікація поля комплексних чисел. Стереографічна проекція. Сфера Рімана.
  6. Функція комплексної змінної. Означення, однозначні, багатозначні, багатолистні функції. Аналітичні функції. Приклади.
  7. Функція комплексної змінної. Неперервні функції. Інтеграл від функції комплексної змінної. Інтеграл від аналітичної функції по замкненому контуру.
  8. Похідна функції комплексної змінної. Формальні похідні Коші. Аналітична функція. Умови Коші-Рімана.
  9. Умови Коші-Рімана в декартових, полярних і довільних ортогональних координатах.
  10. Аналітичні функції. Означення та основні властивості аналітичних функцій. Приклад.
  11. Геометрічна інтерпретація аналітичної функції. Зміст модуля та аргумента похідної. Поняття конформного відображення. Приклад.
  12. Інтеграл вздовж замкненого контура від аналітичної функції в однозв'язній та багатозв'язній області.
  13. Інтегральна формула Коші. Теорема про середнє значення. Теорема про максимум модуля.
  14. Формула Коші для похідної аналітичної функції. Оцінки модуля похідної аналітичної функції. Нескінченна диференційовність аналітичної функції.
  15. Три означення аналітичної функції. Теорема Ліувілля. Теорема Морера.


Модульна контрольна робота № 1 (2 год).

Контрольна робота СРС (2 год).


Змістовий модуль №2 «Теорія лишків»


Тема № 6. «Аналітичні функції і степеневі ряди»


Лекція № 5. Представлення аналітичної функції степеневим рядом (2 год).

Нулі аналітичної функції. Єдиність завдання аналітичної функції. Аналітичне продовження. Представлення рядом Лорана однозначної функції, що аналітична в кільці.


Семінар № 7 Ряд Лорана (1 год).

Розклад функцій, що є аналітичними у кільці в ряд Лорана. Область збіжності ряду Лорана.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Тема № 7. «Особливі точки аналітичної функції»


Лекція № 6. Класифікація особливих точок (2 год).

Класифікація особливих точок однозначних аналітичних функцій. Цілі функції. Мероморфні функціЇ. Поведінка однозначної аналітичної функції в околі в околі полюса та суттєво особливої точки.


Семінар № 7. Особливі точки (1 год).

Дослідження особливих точок аналітичних функцій.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Тема № 8. «Лишки і методи їх обрахунку»


Лекція № 7. Теорія лишків (2 год).

Означення лишка. Методи обрахунку лишка однозначної аналітичної функції. Обчислення лишка в полюсі. Лишок в нескінченно віддаленій точці. Основна теорема теорії лишків. Обчислення контурних інтегралів. Обчислення невласних інтегралів дійсного аналізу за допомогою теорії лишків


Семінар № 8. Обчислення лишків (1 год).

Обчислення лишків в однозначних особливих точках аналітичних функцій.


Завдання для самостійної роботи (6 год).

Вивчення матеріалів лекції, вивчення тем: логарифмічний лишок, принцип аргументу, підрахунок кількості нулів аналітичної функції за рекомендованою літературою, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Тема № 9. «Обчислення інтегралів за допомогою лишків»


Семінар № 9. Обчислення найпростіших інтегралів (2 год).

Обчислення інтегралів уздовж замкнених контурах за допомогою лишків. Обчислення визначених інтегралів, що містять раціональні функції від тригонометричних функцій.


Семінар № 10. Обчислення невласних інтегралів (1 год).

Обчислення невласних інтегралів за допомогою теорії лишків.


Завдання для самостійної роботи (4 год).

Опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Тема № 10. «Плоскі векторні поля і фізичний зміст аналітичної функції»


Лекція № 8. Плоскі векторні поля (2 год).

Потенціальні та соленоідальні поля. Комплексний потенціал. Побудува еквіпотенціалней та силових ліній плоского векторного поля за комплексним потенціалом. Аналітична функція як комплексний потенціал. Критичні та особливі точки та їх фізична інтерпретація


Лекція № 9. Фізичний зміст аналітичної функції (2 год).

Розрахунок підйомної сили крила літака. Формула Жуковського. Електростатичне поле на краю плоского конденсатора. Конденсатор Роговського.


Семінар № 10. Плоскі векторні поля (1 год).

Побудова еквіпотенціалей та силових ліній плоского векторного поля за комплексним потенціалом. Електростатичне поле на краю плоского конденсатора. Конденсатор Роговського.


Завдання для самостійної роботи (5 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 8].


Контрольні запитання

  1. Представлення аналітичної функції степеневим рядом. Нулі аналітичної функції. Єдиність завдання аналітичної функції. Аналітичне продовження. Приклади.
  2. Представлення рядом Лорана однозначної функції, що аналітична в кільці.
  3. Класифікація особливих точок однозначних аналітичних функцій. Цілі функції. Мероморфні функціЇ.
  4. Класифікація особливих точок однозначної аналітичної функції. Поведінка однозначної аналітичної функції в околі в околі полюса та суттєво особливої точки. Приклад.
  5. Означення лишка. Методи обрахунку лишка однозначної аналітичної функції. Обчислення лишка в полюсі. Лишок в нескінченно віддаленій точці.
  6. Основна теорема теорії лишків. Обчислення контурних інтегралів. Приклад.
  7. Обчислення невласних інтегралів дійсного аналізу за допомогою теорії лишків. Приклад.
  8. Логарифмічний лишок. Основна теорема алгебри.
  9. Плоскі векторні поля. Потенціальні та соленоідальні поля. Комплексний потенціал. Побудова еквіпотенціалей та силових ліній плоского векторного поля за комплексним потенціалом.
  10. Аналітична функція як комплексний потенціал. Критичні та особливі точки та їх фізична інтерпретація. Приклад
  11. Фізичний зміст аналітичної функції. Розрахунок підйомної сили крила літака. Формула Жуковського. Електростатичне поле на краю плоского конденсатора. Конденсатор Роговського.


Модульна контрольна робота № 2 (2 год).

Контрольна робота СРС (2 год).


Змістовий модуль №3 «Конформні відображення і задача Діріхле»


Тема № 11. «Задача Діріхле»


Лекція № 10. Задача Діріхле (2 год).

Розв'язання задачі Діріхле за допомогою функції Гріна. Функція Гріна задачі Діріхле. Означення, фізичний зміст. Формула Гріна.


Лекція № 11. Функція Гріна (2 год).

Побудова функції Гріна для півплощини та круга. Розв'язання задачі Діріхле для круга. Формула Пуассона. Розв'язання задачі Діріхле для півплощини. Формула Шварца.


Семінар № 11. Функція Гріна (2 год).

Побудова функцій Гріна задачі Діріхле для елементарних областей.


Завдання для самостійної роботи (6 год).

Вивчення матеріалів лекції, вивчення тем: гармонічні функції, аналітичні та спряжені гармонічні функції, побудова гармонічної функції за спряженою, інваріантність оператора Лапласа відносно конформних відображень, .опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Тема № 12. «Конформні відображення»


Лекція № 12. Основна задача теорії конформних відображень (2 год).

Формулювання основної задачі теорії конформних відображень. Теорема Рімана. Нормування конформного відображення.


Семінар № 12. Дробово-лінійні відображення (2 год).

Дослідження конформних відображень дробово-лінійними функціями.


Семінар № 13. Конформні відображення елементарними функціями (2 год).

Дослідження конформних відображень елементарними функціями.


Семінар № 14. Конформні відображення елементарних областей (1 год).

Дослідження конформних відображень елементарних областей.


Завдання для самостійної роботи (5 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 7, 8, 12].


Тема № 13. «Відображення багатокутників»


Лекція № 13. Відображення багатокутників (2 год).

Відображення багатокутників. Інтеграл Шварца-Христоффеля. Конформне відображенні комплексної півплощини в півплощину та круг.


Семінар № 15. Відображення Шварца-Христоффеля (1 год).

Відображення Шварца-Христоффеля для трикутника і прямокутника


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 3, 7, 12].


Тема № 14. «Операційне числення»


Лекція № 14. Перетворення Лапласа (2 год).

Перетворення Лапласа. Основні властивості. Операційний метод і його застосування до розв'язування лінійних інтегральних рівнянь.


Семінар № 16. Перетворення Лапласа (2 год).

Перетворення Лапласа. Операційне числення.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [1, 2, 3, 7, 12].


Тема № 15. «Аналітична теорія диференціальних рівнянь другого порядку»


Лекція № 15. Звичайні та особливі точки (2 год).

Аналітична теорія диференціальних рівнянь другого порядку. Звичайні та особливі точки.


Лекція № 16. Матриця монохромії (2 год).

Аналітична теорія диференціальних рівнянь другого порядку. Поведінка розв'язка диференціального рівняння в околі звичайної та особливої точки. Матриця монохромії.


Семінар № 17. Звичайні та особливі точки (2 год).

Аналітична теорія диференціальних рівнянь другого порядку. Звичайні та особливі точки.


Завдання для самостійної роботи (4 год).

Вивчення матеріалів лекції, опрацювання семінарських занять, виконання домашнього завдання.


Рекомендована література: [3].


Тема № 16. «Кватерніони і рівняння Максвела»


Лекція № 17. Кватерніони (2 год).

Кватерніони і операції з ними. Алгебра кватерніонів. Фізичне застосування — рівняння Максвела.


Завдання для самостійної роботи (2 год).

Вивчення матеріалів лекції — 2 год.


Рекомендована література: [1, 10].


Контрольні запитання

  1. Гармонічні функції. Аналітичні та спряжені гармонічні функції. Побудова гармонічної функції за спряженою. Приклад.
  2. Інваріантність оператора Лапласа відносно конформних відображень.
  3. Задача Діріхле. Розв'язання задачі Діріхле за допомогою функції Гріна. Приклади.
  4. Функція Гріна задачі Діріхле. Означення, фізичний зміст. Формула Гріна.
  5. Означення та фізичний зміст функції Гріна. Побудова функції Гріна для півплощини та круга. Фізичний зміст.
  6. Розв'язання задачі Діріхле для круга. Формула Пуассона. Приклад.
  7. Розв'язання задачі Діріхле для півплощини. Формула Шварца. Приклади.
  8. Основна задача теорії конформних відображень. Теорема Рімана. Нормування конформного відображення. Відображення багатокутників. Інтеграл Крістофеля-Шварца. Приклад.
  9. Конформне відображенні комплексної півплощини в півплощину та круг.
  10. Перетворення Лапласа. Основні властивості. Приклад.
  11. Операційний метод і його застосування до розв'язування лінійних інтегральних рівнянь типу згортки. Приклад.
  12. Операційний метод і його застосування до розв'язування звичайних диференціальних рівнянь.
  13. Аналітична теорія диференціальних рівнянь другого порядку. Звичайні та особливі точки. Поведінка розв'язка диференціального рівняння в околі звичайної та особливої точки. Матриця монодромії.
  14. Кватерніони і операції з ними. Алгебра кватерніонів. Фізичне застосування — рівняння Максвела.


Модульна контрольна робота № 3 (2 год).

Контрольна робота СРС (2 год).


Організація самостійної роботи студентів


Перелік питань змістових модулів, винесених на самостійну роботу:

  1. Змістовий модуль № 1, тема № 2.

Тема: «Елементарні функції комплексної змінної та їх властивості».

План:
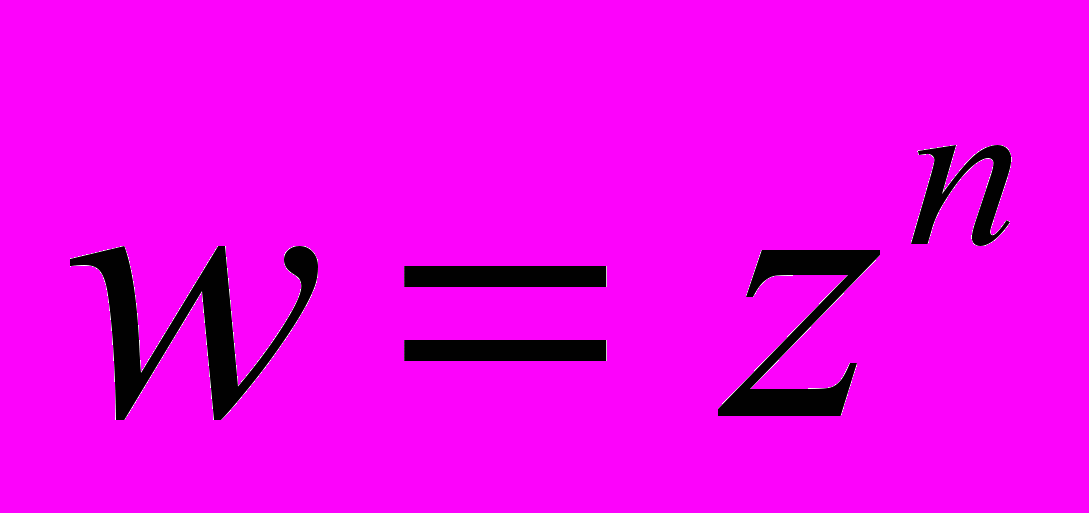    1. Функції і 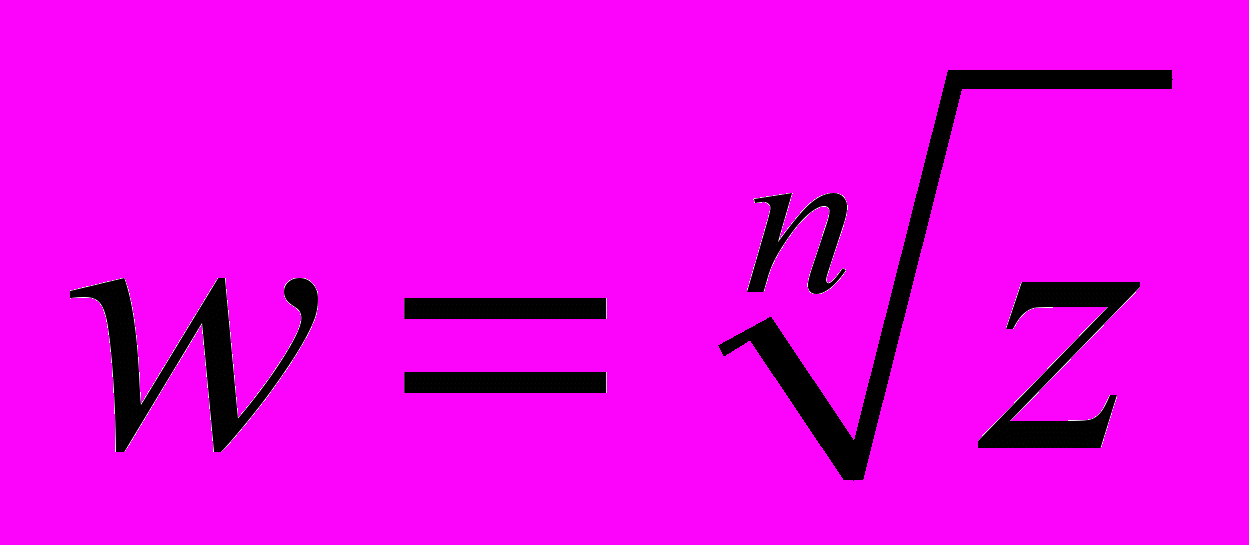[1, п.6, стор. 23-27];
    2. Функція Жуковського 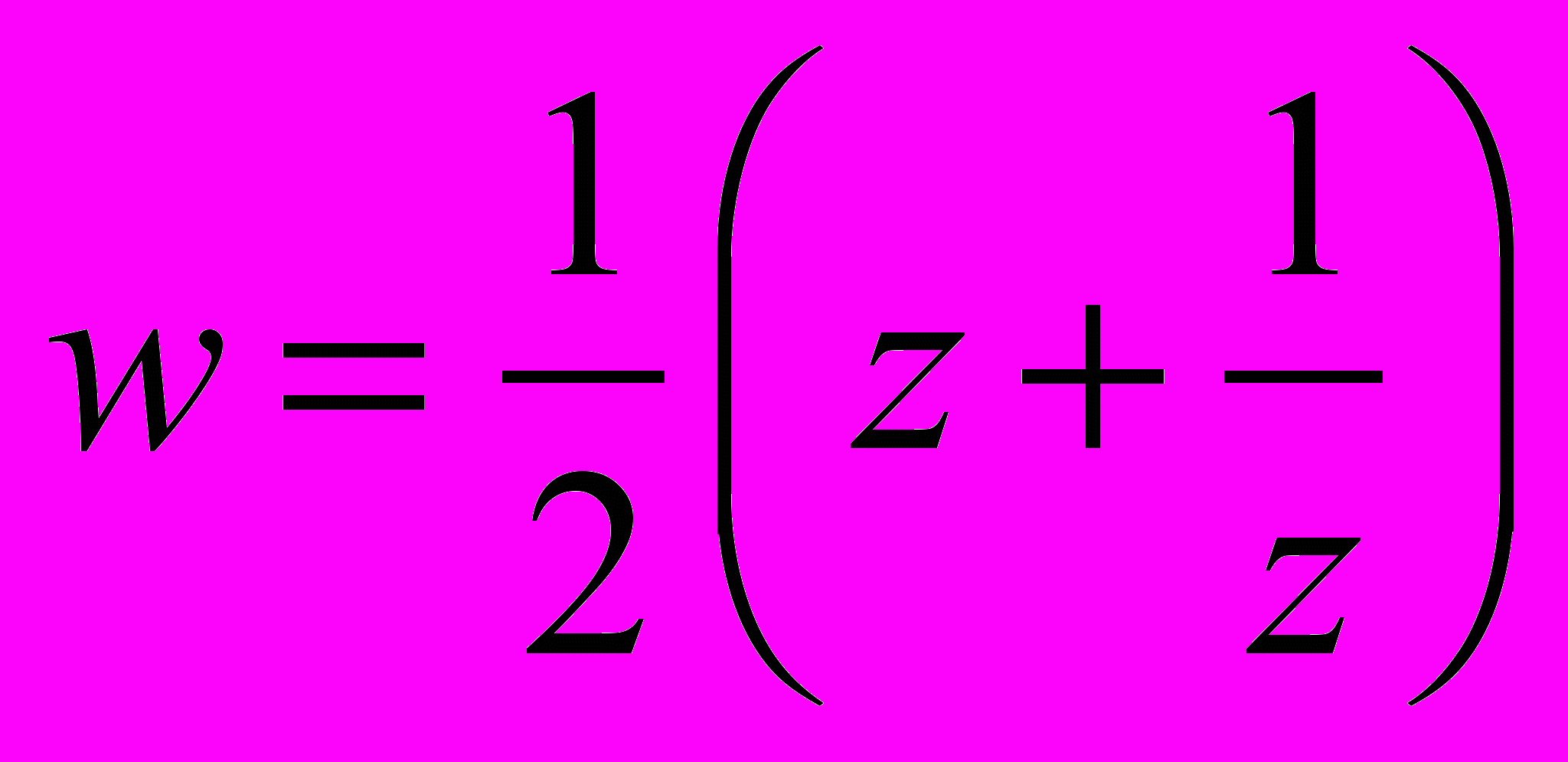[1, п.7, стор. 27-30];
    3. Показникова функція і логарифм [1, п.8, стор. 30-34];
    4. Тригонометричні і гіперболічні функції [1, п.9, стор. 34-39];
    5. Узагальнена степенева функція 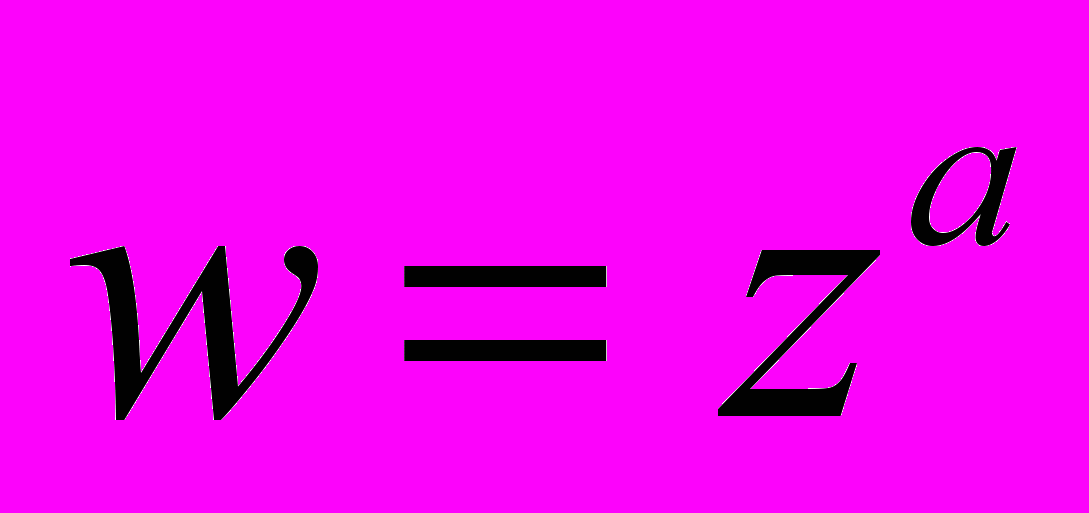[1, п.10, стор. 39-40].



  1. Змістовий модуль № 2, тема № 8.

Тема: «Логарифмічний лишок».

План:
    1. Означення логарифмічного лишка [2, § 3.1, стор. 143-144];
    2. Принцип аргументу. Підрахунок кількості нулів аналітичної функції. Теорема Руше [1, п.75, стор. 424-425] ; [2, § 3.2, стор. 145-147].



  1. Змістовий модуль № 3, тема № 11.

Тема: «Гармонічні функції».

План:
    1. Означення та властивості гармонічних функцій; побудова гармонічної функції за спряженою [1, п.41, п.42, стор. 186-200], [2, § 7.1, стор. 184-185];
    2. Інваріантність оператора Лапласа відносно конформних відображень [2, §7.2, стор. 185-187].

Перелік питань, які виносяться на залік

  1. Комплексні числа. Означення, модуль та аргумент комплексного числа. Зображення комплексних чисел. Тригонометрична та показникова форми комплексного числа. Приклад.
  2. Основні операції над комплексними числами та поле комплексних чисел. Алгебраїчна замкненість поля комплексних чисел.
  3. Невпорядкованість комплексних чисел.
  4. Послідовності комплексних чисел. Граничні точки.
  5. Нескінченно віддалена точка та компактифікація поля комплексних чисел. Стереографічна проекція. Сфера Рімана.
  6. Функція комплексної змінної. Означення, однозначні, багатозначні, багатолистні функції. Аналітичні функції. Приклади.
  7. Функція комплексної змінної. Неперервні функції. Інтеграл від функції комплексної змінної. Інтеграл від аналітичної функції по замкненому контуру.
  8. Похідна функції комплексної змінної. Формальні похідні Коші. Аналітична функція. Умови Коші-Рімана.
  9. Умови Коші-Рімана в декартових, полярних і довільних ортогональних координатах.
  10. Аналітичні функції. Означення та основні властивості аналітичних функцій. Приклад.
  11. Геометрична інтерпретація аналітичної функції. Зміст модуля та аргумента похідної. Поняття конформного відображення. Приклад.
  12. Інтеграл вздовж замкненого контуру від аналітичної функції в однозв'язній та багатозв’язній області.
  13. Інтегральна формула Коші. Теорема про середнє значення. Теорема про максимум модуля.
  14. Формула Коші для похідної аналітичної функції. Оцінки модуля похідної аналітичної функції. Нескінченна диференційовність аналітичної функції.
  15. Три означення аналітичної функції. Теорема Ліувілля. Теорема Морера.
  16. Представлення аналітичної функції степеневим рядом. Нулі аналітичної функції. Єдиність завдання аналітичної функції. Аналітичне продовження. Приклади.
  17. Представлення рядом Лорана однозначної функції, що аналітична в кільці.
  18. Класифікація особливих точок однозначних аналітичних функцій. Цілі функції. Мероморфні функції.
  19. Класифікація особливих точок однозначної аналітичної функції. Поведінка однозначної аналітичної функції в околі в околі полюса та суттєво особливої точки. Приклад.
  20. Означення лишка. Методи обрахунку лишка однозначної аналітичної функції. Обчислення лишка в полюсі. Лишок в нескінченно віддаленій точці.
  21. Основна теорема теорії лишків. Обчислення контурних інтегралів. Приклад.
  22. Обчислення невласних інтегралів дійсного аналізу за допомогою теорії лишків. Приклад.
  23. Логарифмічний лишок. Основна теорема алгебри.
  24. Плоскі векторні поля. Потенціальні та соленоідальні поля. Комплексний потенціал. Побудова еквіпотенціалней та силових ліній плоского векторного поля за комплексним потенціалом.
  25. Аналітична функція як комплексний потенціал. Критичні та особливі точки та їх фізична інтерпретація. Приклад
  26. Фізичний зміст аналітичної функції. Розрахунок підйомної сили крила літака. Формула Жуковського. Електростатичне поле на краю плоского конденсатора. Конденсатор Роговського.
  27. Гармонічні функції. Аналітичні та спряжені гармонічні функції. Побудова гармонічної функції за спряженою. Приклад.
  28. Інваріантність оператора Лапласа відносно конформних відображень.
  29. Задача Діріхле. Розв'язання задачі Діріхле за допомогою функції Гріна. Приклади.
  30. Функція Гріна задачі Діріхле. Означення, фізичний зміст. Формула Гріна.
  31. Означення та фізичний зміст функції Гріна. Побудова функції Гріна для півплощини та круга. Фізичний зміст.
  32. Розв'язання задачі Діріхле для круга. Формула Пуассона. Приклад.
  33. Розв'язання задачі Діріхле для півплощини. Формула Шварца. Приклади.
  34. Основна задача теорії конформних відображень. Теорема Рімана. Нормування конформного відображення. Відображення багатокутників. Інтеграл Крістофеля-Шварца. Приклад.
  35. Конформне відображенні комплексної півплощини в півплощину та круг.
  36. Перетворення Лапласа. Основні властивості. Приклад.
  37. Операційний метод і його застосування до розв'язування лінійних інтегральних рівнянь типу згортки. Приклад.
  38. Операційний метод і його застосування до розв'язування звичайних диференціальних рівнянь.
  39. Аналітична теорія диференціальних рівнянь другого порядку. Звичайні та особливі точки. Поведінка розв'язка диференціального рівняння в околі звичайної та особливої точки. Матриця монодромії.
  40. Кватерніони і операції з ними. Алгебра кватерніонів. Фізичне застосування — рівняння Максвела.



V семестр


Змістовий модуль №4 «Метод відокремлення змінних-1»