Робоча програма навчальної дисципліни для студентів (назва навчальної дисципліни)

Вид материала

Содержание

7:4 Мета та завдання навчальної дисципліни
У результаті вивчення даного курсу студент повинен
Структура навчальної дисципліни
Модуль 1. Границя числової послідовності.
Модуль 2. Числові ряди.
Модуль 3. Границя функції.
Модуль 4. Диференціальне числення функцій однієї змінної.
Усього годин

Подобный материал:

1 2 3 4 5

Примітка.

Співвідношення кількості годин аудиторних занять до самостійної і індивідуальної роботи становить:

для денної форми навчання

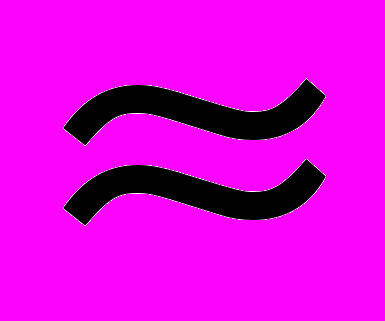7:4

Мета та завдання навчальної дисципліни

Мета курсу полягає у наданні майбутнім спеціалістам знань у галузі сучасного математичного аналізу.

Завданням курсу є навчання студентів теоретичним основам і методам математичного аналізу та застосуванню цих методів для розв’язання різноманітних задач теоретичного та практичного характеру.

У результаті вивчення даного курсу студент повинен

знати:

– властивості границь числових послідовностей та числових функцій;

– властивості неперервних функцій ;

– диференціальне числення функцій однієї та багатьох змінних;

– теорію інтеграла Рімана на відрізку та теорію кратних інтегралів Рімана;

– теорію збіжності невласних інтегралів;

– теорію збіжності числових рядів;

– теорію рівномірної збіжності функціональних послідовностей та рядів;

– теорію степеневих рядів;

– елементи теорії метричних, нормованих та евклідових просторів;

– елементи теорії інтегралів, що залежать від параметру;

– елементи теорії інтеграла Стілтьєса;

– теорію криволінійних та поверхневих інтегралів першого роду;

– теорію криволінійних та поверхневих інтегралів другого роду;

– класичні формули Гріна, Гаусса-Остроградського та Стокса;

– основи теорії векторних полів;

– елементи теорії рядів Фур’є;

– властивості перетворення Фур’є та інтегралу Фур’є.

вміти:

– знаходити границі послідовностей і функцій;

– оцінювати швидкість зростання нескінченно великих послідовностей;

– досліджувати функції на неперервність;

– диференціювати функції однієї та багатьох змінних;

– користуватися розвиненням функції за формулою Тейлора;

– досліджувати функції на монотонність, екстремум та опуклість;

– будувати графік функції за допомогою диференціального числення;

– знаходити невизначені інтеграли;

– обчислювати визначені інтеграли за Ріманом, подвійні та потрійні інтеграли, криволінійні та поверхневі інтеграли;

– застосовувати інтеграл Рімана в геометрії, механіці, фізиці;

– досліджувати на абсолютну та умовну збіжності невласні інтеграли Рімана;

– досліджувати на абсолютну та умовну збіжності числові ряди;

– досліджувати на рівномірну збіжність функціональні послідовності та ряди;

– отримувати розвинення функцій у ряд Тейлора;

– досліджувати на внутрішній та умовній екстремум функції багатьох змінних;

– обчислювати інтеграли за допомогою Г-функцій та В-функцій;

– застосовувати кратні інтеграли в геометрії, механіці, фізиці;

– застосовувати формули Гріна, Гауса-Остроградського, Стокса для обчислення криволінійних та поверхневих інтегралів;

– застосовувати методи та термінологію векторної теорії полів;

– розкладати функцію у ряд Фур’є та досліджувати його на збіжність;

– здійснювати перетворення Фур’є функції та подавати її у вигляді інтегралу Фур’є.

Програма навчальної дисципліни

І семестр

Модуль 1. Границя числової послідовності.

Логічна символіка, множини, функції, послідовності. Аксіоми дійсних чисел. Обмеженість,

точні межі числової множини.

2. Границя числової послідовності і загальні властивості таких границь. Нескінченно малі та

нескінченно великі послідовності.

3. Теорема Вейерштрасса про збіжність монотонних послідовностей. Число e.

4. Порівняння швидкості зростання послідовностей, асимптотика послідовностей. Символи

О і

.

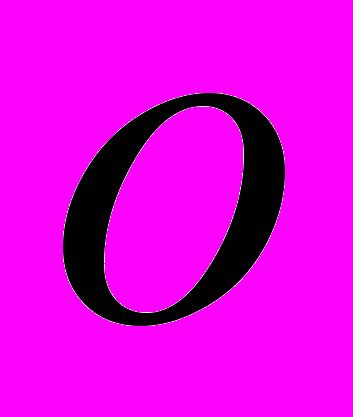5. Часткові границі числової послідовності, верхня та нижня границя послідовності. Принцип

Больцано-Вейєрштрасса для послідовностей.

6. Означення фундаментальної послідовності. Критерій Коші збіжності послідовності.

Модуль 2. Числові ряди.

Означення числового ряду, його часткових сум і збіжності ряду. Найпростіші властивості числових рядів. Критерій Коші та необхідна умова збіжності числового ряду.
Ознаки збіжності рядів з невід’ємними членами.
Абсолютна та умовна збіжність рядів. Ознака Лейбніца.

Модуль 3. Границя функції.

Границя функції за Коші та за Гейне. Загальні властивості границь функцій.
Порівняння функцій, асимптотика функцій, асимптоти графіка функції.
Важливі границі, що пов’язані з елементарними функціями.
Неперервність функції за Коші і за Гейне. Локальні властивості неперервних функцій. Неперервність елементарних функцій.
Властивості функцій, неперервних на відрізку.
Точки розриву та їх класифікація.

Модуль 4. Диференціальне числення функцій однієї змінної.

Означення диференційовної функції в точці. Диференціал та похідна функції в точці.

Механічне та геометричне тлумачення понять похідної та диференціалу функції. Рівняння дотичної до графіка диференційовної функції.

Правила диференціювання функцій. Похідні елементарних функцій.
Теореми Ферма, Ролля, Лагранжа, Коші та їх застосування. Правило Лопіталя.
Похідні вищих порядків. Локальна і глобальна формули Тейлора.
Опуклість і точки перегину. Достатня умова опуклості у термінах другої похідної.
Нерівність Йенсена та її наслідки.

ІІ семестр

Модуль 5. Невизначений інтеграл.

Означення первісної функції на проміжку. Невизначений інтеграл і його властивості. Таблиця первісних деяких елементарних функцій. Формула заміни змінної та формула інтегрування частинами для невизначеного інтегралу.
Інтегрування раціональних функцій. Інтегрування деяких ірраціональностей та деяких трансцендентних функцій.

Модуль 6. Визначений інтеграл та його застосування.

Означення інтегральних сум Рімана та інтеграла Рімана. Необхідна умова інтегрованості функції за Ріманом.
Нижні (верхні) суми Дарбу та їх властивості. Означення нижнього (верхнього) інтеграла Дарбу.

Критерії Дарбу і Рімана інтегрованості функції за Ріманом.

Класи функцій, інтегрованих за Ріманом
Властивості визначеного інтеграла.
Неперервність та диференційовність функції, заданої інтегралом Рімана із змінною верхньою межею інтегрування. Існування первісної у неперервної функції.
Формула Ньютона-Лейбніца. Відновлення функції за її похідною. Формула інтегрування частинами для інтеграла Рімана. Теорема про заміну змінної в інтегралі Рімана.
Застосування визначеного інтеграла до геометрії: площа криволінійної трапеції, довжина кривої, об’єм тіла обертання. Механічні застосування інтеграла.
Невласний інтеграл по необмеженому проміжку та від необмеженої функції. Обчислення невласних інтегралів.
Ознака порівняння збіжності невласних інтегралів і її наслідки. Еталонні інтеграли. Зв'язок з числовими рядами.
Абсолютна та умовна збіжності невласних інтегралів. Головне значення невласного інтеграла в розумінні Коші.
В- і Г- функції Ейлера та їх застосування. Формула Стірлінга для Г-функції та факторіала.

Модуль 7. Функціональні ряди. Степеневі ряди.

Поточкова та рівномірна збіжність. Критерій Коші і ознака Вейерштрасса рівномірної збіжності функціональних рядів.
Теорема про неперервність граничної функції. Почленне інтегрування і диференціювання функціонального ряду.
Означення степеневого ряду. Радіус та інтервал збіжності степеневого ряду. Властивості суми степеневого ряду, почленне диференціювання та інтегрування степеневих рядів. Ряд Тейлора. Ряд Маклорена основних елементарних функцій. Формула Ейлера.
Арифметичні дії над степеневими рядами. Твірна функція числової послідовності.

Модуль 8. Диференціальне числення функцій кількох змінних.

Простір 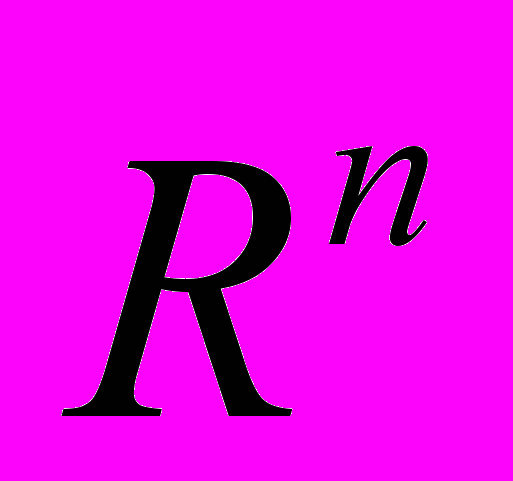. Збіжність і компактність в 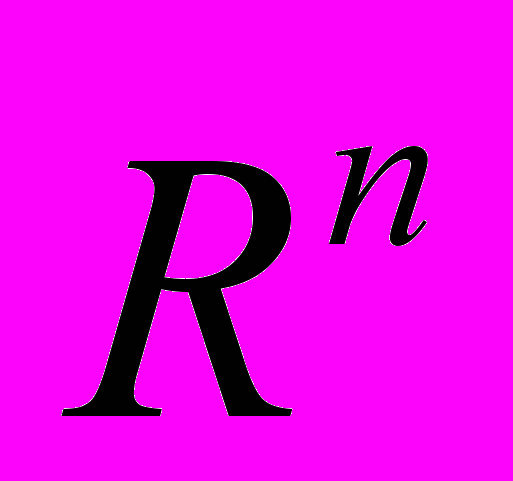. Локальні та глобальні властивості неперервних функцій кількох змінних.
Диференційовність функції кількох змінних в точці, умови диференційовності. Дотична і нормаль до поверхні. Похідна функції за напрямком і градієнт.
Похідна композиції функцій інваріантність форми першого диференціала. Теорема Лагранжа та її наслідки.
Похідні та диференціали вищих порядків. Теорема про рівність змішаних похідних. Формула Тейлора.
Локальний екстремум функції кількох змінних. Метод найменших квадратів.
Теореми про неявну функцію та неявне відображення. ^{Функціональна залежність і незалежність гладких функцій. Умовний екстремум.}

ІІІ семестр

Модуль 9. Кратні інтеграли Рімана.

Означення інтегральних сум Рімана, інтеграла Рімана по брусу та інтегровної за Ріманом функції на брусі. Необхідна умова інтегровності за Ріманом. Верхні та нижні суми Дарбу та їх властивості.
Множини об’єму нуль і міри нуль. Інтегровність неперервної на брусі функції. Інтеграл по обмеженій множині в 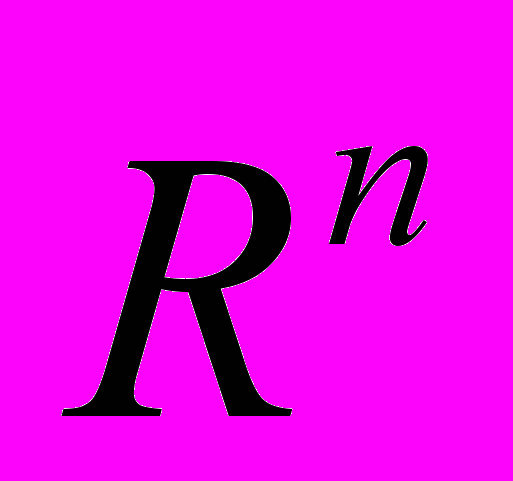. Множини, вимірні за Жорданом. Зведення кратного інтеграла по брусу і циліндроїду до повторних.
Заміна змінних в кратних інтегралах.

Модуль 10. Криволінійні та поверхневі інтеграли першого роду.

^{Означення криволінійного інтеграла 1-го роду по простій гладкій кривій, незалежність від вибору п}^{араметризації та зведення його до інтеграла Рімана.}
^{Означення поверхневого інтеграла 1-го роду по елементарній гладкій поверхні.}^{Площа гладкої поверхні. Формули для обчислення поверхневих інтегралів 1-го роду.}

Модуль 11. Криволінійні та поверхневі інтеграли другого роду.

^{Означення і обчислення}^{криволінійного та}^{поверхневого інтеграла 2-го роду. Приклади (інтеграли роботи та потоку).}
Властивості поверхневих інтегралів 2-го роду. Зв’язок між поверхневими інтегралами 1-го и 2-го родів^.
^{Формули Гріна, Стокса та Гаусса-Остроградського. Дивергенція і ротор. Поняття про диференціальні форми і загальну формулу Стокса.}
Означення потенціального векторного поля и його потенціалу. Необхідна умова потенціальності поля. Робота сил у потенціальному полі. Критерії потенціальності векторного поля.

Модуль 12. Ряди Фур’є та інтеграл Фур’є.

Ортогональні та ортонормовані системи векторів у лінійних просторах зі скалярним добутком. Система тригонометричних функцій на [-,].
Коефіцієнти Фур’є і ряд Фур’є вектора у просторі зі скалярним добутком відносно ортонормованої або ортогональної послідовності. Тригонометричний ряд Фур’є на [-,].
Нерівність Бесселя і рівність Парсеваля. Теорема Ляпунова про повноту тригонометричної системи функцій.
Інтегральні зображення для часткових сум тригонометричних рядів Фур’є. Поточкова та рівномірна збіжність тригонометричних рядів Фур’є. Зв’язок між степенем гладкості функції та швидкістю прямування до нуля коефіцієнтів її тригонометричного ряду Фур’є.
Теорема Фейєра. Теореми Вейєрштрасса про рівномірну апроксимацію неперервних функцій тригонометричними та алгебраїчними поліномами.
Означення перетворення Фур’є та інтеграла Фур’є. Властивості перетворення Фур’є . Формула обернення. Приклади.

Структура навчальної дисципліни

І семестр

Назви модулів	Кількість годин
	Денна форма						Заочна форма
	Усього	у тому числі					Усього	у тому числі
	Усього	л	п	лаб	інд	ср	Усього	л	п	лаб	інд	ср
1	2	3	4	5	6	7	8	9	10	11	12	13
Модуль 1. Границя числової послідовності.	30	12	8			10	25	2	5			18
Модуль 2. Числові ряди.	12	4	4			4	23	1	2			20
Модуль 3. Границя функції.	22	8	8			6	24	1	3			20
Модуль 4. Диференціальне числення функцій однієї змінної.	34	12	16			6	26	2	4			20
Екзамен	10					10	10					10
Усього годин	108	36	36			36	108	6	14			88

Blog

Робоча програма навчальної дисципліни для студентів (назва навчальної дисципліни)

Содержание

Усього годин