Увеличение оптическое

Вид материала

Документы

Содержание Уравнение состояния Планка законом излучения. Уровни энергии Квантовые переходы Усиление оптического излу­чения Нелинейная оптика). Усиление ультразвука Н. На широте Москвы на уровне моря g= Классификация ускорителей. Историческая справка. Лоренца сила). В>. При увеличении энергии ч-цы нужно либо уменьшать частоту у (фазотрон), либо увеличивать магн. поле В, заворачивающее ч-цы по круговой орбите, используется и для фокусировки. Если В

Подобный материал:

• Оптическое оборудование, 171.18kb.
• Хованскова Инна Александровна, 37.43kb.
• Полиграфический словарь, 499.28kb.
• Увеличение продаж – возможно ли это сейчас?, 24.11kb.
• Оптическое оборудование, 440.32kb.
• Машиностроение, 219.74kb.
• Кроэкономической ситуации стало сохранение и увеличение денежных сбережений населения,, 61.54kb.
• Патофизиология регионарного кровообращения и микроциркуляции, 124.19kb.
• Увеличение пенсионного возраста для женщин, 218.59kb.
• Федеральная целевая программа «Жилище» на 2002-2010 годы и входящие в ее состав подпрограммы, 116.2kb.

УРАВНЕНИЕ СОСТОЯНИЯ, связыва­ет давление р., объём V и темп-ру Т фи­зически однородной системы в состоя­нии равновесия термодинамического: f(p, V, Т)=0. Это ур-ние наз. тер­мическим У. с., в отличие от калорического У. с., опреде­ляющего внутреннюю энергию U сис­темы как ф-цию к.-л. двух из трёх параметров р, V, Т. Термич. У. с. позволяет выразить давление через объём и темп-ру p = p(V, Т) и опреде-

789


пить элем. работу A=pV при беско­нечно малом расширении системы V. У. с. явл. необходимым дополнением к термодинамич. законам, к-рое делает возможным их применение к реаль­ным в-вам. Оно не может быть выведе­но с помощью одних только законов термодинамики, а определяется из опыта или рассчитывается теоретиче­ски на основе представлений о строе­нии в-ва методами статистической физики. Из первого начала термодина­мики следует лишь существование калорич. У. с., а из второго начала тер­модинамики — связь между термич. и калорическим У. с.: (дU/дV)_T=T(дp/дT)v-p, откуда вытекает, что для идеального газа внутр. энергия не зависит от объёма (дUlдV)_T=0. Для вычисления как термич., так и калорич. У. с. достаточно знать любой из потенциалов термодинамических в виде ф-ции своих параметров. Напр., если известна Гельмгольца энергия F (свободная энергия) как ф-ция Т и V, то У. с. находят дифференцированием:

p=-(дF/дV)_T, U=-T²(д/дT)(F/T)_V.

Примерами У. с. для газов могут служить Клапейрона уравнение для идеального газа pv=RT, где R — газовая постоянная, v — объём 1 моля газа; Ван-дер-Ваальса уравнение (р+a/v²)(v—b) = RT, где а и b — посто­янные, зависящие от природы газа и учитывающие влияние сил притяжения между молекулами и конечность их объёма; вириальное У. с. для неидеального газа рv/RT=1+B (T)/v+C(T)/v²+. . . , где В(T), С(Т). . .— 2-й, 3-й и т. д. вириальные коэфф., зависящие от сил вз-ствия между молекулами (см. Газ). Вириальное ур-ние позволяет объяснить многочисл. эксперим. результаты на осно­вании простых моделей межмолекуляр­ного взаимодействия в газах. Были предложены также разл. эмпирич. У. с., основанные на эксперим. данных о теплоёмкости и сжимаемости газов. У. с. неидеальных газов указывает на существование критич. точки (с параметрами р_к, V_к, T_к), в к-рой газо­образная и жидкая фазы становятся идентичными (см. Критическое состоя­ние). Если У. с. представить в виде приведённого У. с., т. е. в безразмер­ных переменных р/р_к, V/V_к, T/T_к, то при не слишком низких темп-рах это ур-ние мало меняется для разл. в-в (закон соответственных состояний). Для жидкостей из-за сложности учёта всех особенностей вз-ствия моле­кул пока не удалось получить общее теор. У. с. Ур-ние Ван-дер-Ваальса, хотя и применяют для качеств. оценки поведения жидкостей, но по существу оно неприменимо ниже критич. точ­ки, когда возможно сосуществование жидкой и газообразной фаз. У. с., хорошо описывающее св-ва ряда простых жидкостей, можно получить из приближённых теорий жидкого состоя­ния типа теории свободного объёма или дырочной теории (см. Жидкость). Знание распределения вероятности взаимного расположения молекул (парной корреляц. ф-ции) принципи­ально позволяет вычислить У. с. жид­кости, но эта задача очень сложна и полностью не решена даже с помощью вычислит. машин.

Для получения У. с. тв. тел исполь­зуют теорию колебаний кристалличе­ской решётки, но пока универсального У. с. для тв. тел нет.

Для равновесного излучения, или фотонного газа, У. с. определяется Планка законом излучения.

Для магн. сред элем. работа при на­магничивании равна: А = -НМ, где М — магн. момент в-ва, Н — напря­жённость магн. поля. Следовательно, зависимость М = М(Н, Т) представ­ляет собой магнитное У. с. Для диэлектриков элем. работа равна: A=ЕР, где Р— поляризация, Е— напряжённость электрич. поля, и У. с. имеет вид Р=Р(Е, Т).

• Майер Дж., Гепперт-Майер М., Статистическая механика, пер. с англ., 2 изд., М., 1980, гл. 8; И с и х а р а А., Статистическая физика, пер. с англ., М., 1973, гл. 5; Вукалович М. П., Новиков И. И., Уравнение со­стояния реальных газов, М.— Л., 1948; М е й с о н Э., Сперлинг Т., Вириаль­ное уравнение состояния, пер. с англ., М., 1972; Ашкрофт Н., М е р м и н Н., Физика твердого тела, пер. с англ., М., 1979.

Д. Н. Зубарев.

УРОВНИ ЭНЕРГИИ, возможные зна­чения энергии квант. систем (атомов, молекул, ат. ядер и т. д.), состоящих из микрочастиц и подчиняющихся за­конам квантовой механики. Внутр. энергия квант. систем может прини­мать только определённые дискр. зна­чения: ξ₀, ξ₁, ξ₂, ... , (ξ₀<ξ₁<ξ₂...), соответствующие устойчивым (стационарным) состояниям системы. Графически эти состояния можно изоб­разить по аналогии с потенц. энергией



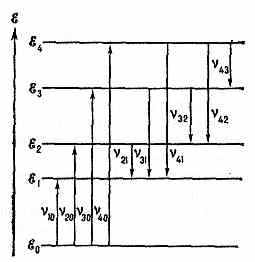
тела, поднятого на разл. высоты (уров­ни), в виде диаграммы У. э. (рис.). Каждому значению энергии соответст­вует горизонтальная линия, проведён­ная (в определ. масштабе) на высоте ξ_i (i=0, 1, 2, ...). Совокупность У. э. рассматриваемой квант. системы об­разует её энергетический спектр. Нижний уровень ξ₀, соответствующий наименьшей возмож­ной энергии системы, наз. основ­ным, все остальные — ξ₁, ξ₂, ...— возбуждёнными, т. к. для перехода на них необходимо возбудить систе­му — сообщить ей энергию.

Квантовые переходы между У. э. обозначают на диаграммах вертикаль­ными (или наклонными) прямыми, со­единяющими соответствующие пары У. э. На рис. показаны излучат. пере­ходы с частотами _ik, удовлетворяю­щими условию частот: h_ik=ξ_i-ξ_k; безызлучат. переходы часто обозна­чаются волнистыми линиями. Направ­ление перехода указывают стрелкой: стрелка, направленная вниз, соответ­ствует процессу испускания фотона, стрелка в обратном направлении — процессу поглощения фотона с энер­гией h_ik. Дискр. энергетич. спектру соответствуют дискр. спектры погло­щения и испускания (см. Спектры оп­тические).

Для квант. системы, имеющей в определ. диапазонах значений энер­гии непрерывный энергетич. спектр, на диаграмме получаются непрерыв­ные последовательности У. э. в соот­ветствующих диапазонах. Напр., для атома Н такая непрерывная последо­вательность имеет место при ξ >ξ_, где ξ_ — граница ионизации (см. рис. 1, б в ст. А том), а для эл-на в кристалле получается чередование разрешённых и запрещённых энергетич. зон (см. Диэлектрики, Полупроводники). При излучат. квант. переходах между дискр. У. э. и У. э., относящимися к непрерывной последовательности, а также между непрерывными последо­вательностями У. э. получаются сплошные спектры поглощения и ис­пускания.

Важной хар-кой У. э. являются их ширины (Г), связанные с временем жизни () квант. системы на уровне Г~1/. У. э. тем уже, чем больше время жизни, в согласии с неопреде­лённостей соотношением для энергии и времени (см. Ширина уровня).

При рассмотрении У. э. квант. сис­тем значения энергии принято отсчи­тывать от осн. уровня. Наряду со шкалой энергий, обычно выражаемых в эВ (а для ат. ядер в МэВ или кэВ), в спектроскопии применяют пропорцио­нальные ей шкалы частот =ξ/h (в радиоспектроскопии) и волн. чисел v/c=ξ/hc (в оптич. спектроскопии); 1 эВ соответствует 2,4180•10¹⁴ Гц и 8065,5 см^-1. В рентгеновской спектро­скопии применяют ед. энергии ридберг: 1 Ry=13,606 эВ.

В оптич. спектроскопии часто при­меняют термин «спектральный терм», подразумевая под ним значение Т=-ξ/hc, отсчитываемое для атомов от границы ионизации и выражаемое в см^-1.

9 См. лит. при ст. Атом, Молекула, Твёрдое тело, Ядро атомное.

М. А. Ельяшевич.

УСИЛЕНИЕ ОПТИЧЕСКОГО ИЗЛУ­ЧЕНИЯ, увеличение мощности или яркости оптического излучения (ОИ) С

790


помощью спец. устройств. Усиление ОИ может осуществляться коге­рентно в оптич. квантовых усили­телях (ОКУ) или параметрических усилителях (ПУ) и некогерент­но с помощью электронно-оптических преобразователей (ЭОП). Основой ОКУ явл. активная среда, в к-рой под дейст­вием накачки создаётся инверсия населённостей. В качестве активной среды в ОКУ используются те же самые мате­риалы, что и в лазерах. Усиление ОИ в ОКУ осуществляется вследствие эф­фекта вынужденного излучения. Типы ОКУ отличаются способом накачки, активной средой, режимом работы (не­прерывный или импульсный). ОКУ могут усиливать только ОИ с узкой спектр. полосой, совпадающей с поло­сой усиления активной среды. Боль­шие коэфф. усиления получают в неск. ОКУ, расположенных последователь­но друг за другом. ОКУ широко рас­пространены в квантовой электронике, особенно для создания мощных лазер­ных систем. В таких системах могут использоваться неск. параллельных каналов, каждый из к-рых состоит из неск. ОКУ.

Работа параметрич. усилителей ОИ основана на нелинейных оптич. яв­лениях (см. Нелинейная оптика). По­лоса усиления ПУ может перестраи­ваться по частоте в широких пределах.

ЭОП служит для усиления яркости ОИ с широким спектром. В ЭОП на фотокатоде происходит преобразова­ние ОИ в поток эл-нов, усиление пото­ка эл-нов и затем обратное преобразо­вание потока эл-нов в ОИ. При уси­лении происходит также преобразова­ние спектра исходного ОИ в спектр свечения люминофора, к-рый обычно лежит в видимой области. Усиление потока эл-нов в ЭОП осуществляется либо при последоват. преобразовании эл-нов в кванты и обратно в эл-ны в многокамерных ЭОП, либо вследствие вторичной электронной эмиссии в микроканальных пластинах. Коэфф. усиления ЭОП по яркости до­стигают величин ~10⁷. Миним. регист­рируемый входной сигнал в видимой области спектра составляет неск. квантов.

УСИЛЕНИЕ УЛЬТРАЗВУКА в по­лупроводниках, см. Акустоэлектронное взаимодействие. УСКОРЕНИЕ, векторная величина, характеризующая быстроту измене­ния скорости точки по численному значению и по направлению. При пря­молинейном движении точки, когда её скорость v возрастает (или убывает) равномерно, численно У. w=v/t, где v — приращение скорости за проме­жуток времени t. В общем случае вектор У. w=dv/dt=v', он направлен в сторону вогнутости траектории точки и лежит в соприкасающейся плоскости (если траектория точки — плоская кривая, то в плоскости этой кривой).

Проекции У. на прямоуг. декартовы координатные оси Oxyz равны: w_x=v_x,

w_y=v'_y, w_z=v_z', при этом модуль У.

w=(w²_x+w²_y+w²_z). Проекции У. на касательную и гл. нормаль к траекто­рии наз. соответственно касательным (тангенциальным) w_ и нор­мальным (центростремительным) w_n У.; они определяются равенствами: w_=dv/dt=v' и w_n=v²/, где v — чис­ленная величина скорости,  — ради­ус кривизны траектории в соответст­вующей её точке. При этом w=(w²_+w²_n). Касательное У. характе­ризует изменение скорости точки по её численной величине, а норм. У.— по направлению.

У. свободной материальной точки при движении по отношению к инерц. системе отсчёта связано с массой т точки и с действующей силой F равен­ством: mw=F (второй закон Ньютона). Размерность У. LT^-2. Об У. точек вращающегося тела см. Вращатель­ное движение.

• См. лит. при ст. Кинематика.

С. М. Тарг.

УСКОРЕНИЕ СВОБОДНОГО ПАДЕ­НИЯ (ускорение силы тяжести), уско­рение, к-рое приобретает свободная ма­териальная точка под действием силы тяжести. Такое ускорение имел бы центр тяжести любого тела при паде­нии тела на Землю с небольшой высоты в безвоздушном пр-ве. Как и сила тя­жести, У. с. п. зависит от широты ме­ста  и высоты его Н над уровнем моря. Приблизительно У. с. п.

g= 978,049 (1+0,005288 sin-0,000006 sin² 2)-0,0003086 Н.

На широте Москвы на уровне моря g= 981,56 см/с².

УСКОРИТЕЛИ заряженных частиц, устройства для получения заряж. ч-ц (эл-нов, протонов, ат. ядер, ионов) больших энергий с помощью их уско­рения в электрич. поле. Помимо физ. применений, играющих определяющую роль в развитии ускорит. техники, У. начинают всё больше использоваться за пределами физики (химия, биофизи­ка, геофизика) и в прикладных целях (дефектоскопия, стерилизация продук­тов, лучевая терапия и т. п.). У. за­ряженных ч-ц следует отличать от плаз­менных ускорителей, в которых осу­ществляется ускорение электрически нейтральных образований из заря­женных частиц.

Классификация ускорителей. По спо­собу получения ускоряющего поля различают обычные («классические») У., в к-рых ускоряющее поле создаёт­ся внеш. радиотехнич. устройствами (генераторами), и У., в к-рых ускоряю­щее поле создаётся другими заряж. ч-цами (электронным пучком, элект­ронным кольцом, плазменными вол­нами; см. Коллективные методы уско­рения). По типу ускоряемых ч-ц раз­личают электронные У., протонные У. и У. ионов, а по хар-ру траекторий ч-ц - линейные У. (траектории близки к прямым линиям) и циклические (траектории близки к окружности или спирали). По хар-ру ускоряющего поля У. разделяются на резонансные, в к-рых ускорение производится высо­кочастотным электрич. полем и уско­ряемые ч-цы движутся в резонанс с изменением поля, и нерезонансные, в к-рых направление поля за время ускорения не изменяется. В свою очередь, последние делятся на индук­ционные У., где электрич. поле созда­ётся за счёт изменения магн. поля, и высоковольтные У., в к-рых ускоряю­щее поле обусловлено приложенной разностью потенциалов.

Историческая справка. В начальный период (1919—32) развитие У. шло по пути создания генераторов высоких напряжений и их использования для непосредств. ускорения заряж. ч-ц в постоянном электрич. поле. Заряж. ч-цы, проходя от одного полюса ис­точника высокого напряжения к дру­гому, ускорялись в соответствии с ве­личиной напряжения. Этот период за­вершился разработкой электростати­ческого генератора (амер. физик Р. Ван-де-Грааф, 1931) и каскадного генератора (англ. физики Дж. Кокрофт и Э. Уолтон, 1932). Такие уст­ройства, применяемые до сих пор, поз­воляют получить потоки ускоренных ч-ц с энергией ~10⁶ эВ (см. Высоко­вольтный ускоритель). В 1931—44 раз­виваются резонансные методы, в к-рых ускорение производится перем. ВЧ полем. Проходя многократно через ус­коряющий промежуток, ч-ца набирает большую энергию даже при невысоком ускоряющем напряжении. Резонанс­ное ускорение в линейных У. тогда не получило распространения из-за не­достаточного развития радиотехники. Основанные же на этом методе циклич. У.— циклотроны (амер. физик Э. О. Лоуренс) вскоре обогнали в сво­ём развитии высоковольтные У. и поз­волили получить протоны с энергией 10—20 МэВ. В 1940 (амер. физик Д. У. Керст) удалось реализовать циклич. У. эл-нов индукц. типа (бета­трон), идея к-рого выдвигалась ещё в 20-е гг.

Разработка У. совр. типа началась с открытия механизма автофазировки (1944—45, В. И. Векслер и независимо амер. физик Э. М. Макмиллан), позво­лившего существенно повысить энер­гию ускоренных ч-ц в резонансных У. На основе этого принципа разработаны неск. типов циклич. У.: синхротрон, фазотрон, синхрофазотрон, микро­трон. Развитие радиотехники дало возможность создать эфф. линейные резонансные У. Предложенная идея знакопеременной фокусировки (Н. Кристофилос, 1950, Э. Курант, М. Ливингстон, X. Снайдер, США, 1952) существенно повысила достижи­мую энергию в циклич. и линейных У. Предельная энергия для эл-нов (~20 ГэВ) достигнута на линейных

791


У., для протонов (>500 ГэВ) — на циклич. У.

Развитие У. идёт как по пути увели­чения энергии ускоренных ч-ц, так и по пути улучшения хар-к ускоренно­го пучка — увеличения его интенсив­ности и длительности импульса, умень­шения разброса его параметров (каче­ство пучка). Значит. прогресс будет достигнут в связи с применением сверх­проводников в магнитах и ускоряющих системах, внедрением методов автома­тич управления, введением в ускорит. комплекс накопит. колец и систем встречных пучков, расширяющих воз­можности У.

Параллельно развитию перечислен­ных «классич.» У. разрабатываются коллективные методы ускорения, идея к-рых была выдвинута Векслером (1956). Они обещают существенно бо­лее высокий темп ускорения, чем в современных У.

Резонансные методы ускорения на­иболее широко распространены в совр. У. В резонансных У. ч-цы движутся в вакуумных камерах, в к-рых создаёт­ся высокий вакуум (10^-6—10^-8 мм рт. ст.) для ослабления рассеяния ч-ц в газе. Непрерывное ускорение обес­печивается тем, что ч-цы попадают в ускоряющий промежуток всё время в ускоряющей фазе перем. ВЧ электрич. поля, т. е. когда сила действия элект­рич. поля направлена в сторону дви­жения ч-ц. Проходя многократно че­рез ускоряющий промежуток, ч-ца может набрать большую энергию даже при сравнительно невысоком напря­жении на нём. Идеальная, т, н. равно­весная, ч-ца всё время попадает в одну и ту же, равновесную фазу ₀ поля. При каждом прохождении ускоряюще­го промежутка она набирает энергию eV₀cos_o, где е — заряд ч-цы, a V₀ — амплитуда ускоряющего напряжения. Чтобы набрать большую кинетич. энергию W_макс, частица должна совершить очень большое число N=W_макс/eV₀cos₀ прохождений через ускоряющий промежуток. Поэтому для работы У. необходимо обеспечить устойчивость равновесного движения ч-цы: небольшие отклонения в началь­ных данных для ч-ц или небольшие внеш. возмущения (неизбежные откло­нения параметров установки от расчёт­ных, рассеяние на остаточном газе в ускорит. камере и т. п.) не должны приводить к сильному отклонению от равновесной орбиты, т. е. ч-ца долж­на совершать колебат. движение около равновесной ч-цы. Обеспечение устой­чивости движения ч-ц в направлениях, перпендикулярных траектории, наз. фокусировкой, а в направлении траек­тории — фазировкой.

Фазировка обеспечивается в резо­нансных У. механизмом автофазировки, обусловленным зависимостью промежутка времени между двумя следующими друг за другом ускорениями от энергии ξ ч-ц. Благодаря этому одна из двух равновесных фаз ₀ или -₀, для к-рых прирост энер­гии eV₀cos₀ обеспечивает точный ре­зонанс, оказывается устойчивой, т. е. около неё существует область захвата, внутри к-рой ч-цы ко­леблются по фазе относительно равно­весной фазы. Если дТ/дξ>0, то ус­тойчива фаза +₀, лежащая на спа­дающем склоне кривой напряжения, если дT/дtds<0, то устойчива фаза -₀ на восходящем склоне кривой на­пряжения (см. рис. в ст. Автофазироека).

Резонансные циклические ускорите­ли. Движение по почти круговым тра­екториям обеспечивается в цпклич. У. магн. полем (см. Лоренца сила). Связь между ср. радиусом орбиты , ср. магн. полем на орбите <В> и энергией ξ частиц даётся соотноше­нием:



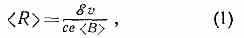
где е — заряд ч-цы, ξ=mc² — полная релятив. энергия ч-цы массы m, рав­ная сумме энергии покоя ξ₀=m₀c² и её кинетич. энергии (m₀— масса покоя ч-цы), v — скорость ч-цы. Пе­риод обращения ч-цы по орбите



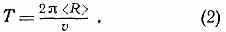
Из (1) и (2) следует связь между ξ, индукцией <В> магн. поля и круго­вой частотой  обращения ч-цы по орбите:



Резонансные циклич. У. различаются по хар-ру управляющего магн. поля и ускоряющего электрич. поля: сущест­вуют У. с постоянным и с переменным (во времени) магн. полем и соответст­венно У. с постоянной и с перем. часто­той _у ускоряющего поля. Частота ускоряющего поля _у должна быть кратна частоте  обращения ускоряе­мой (резонансной) ч-цы: _у=q, где q — целое число, наз. кратностью час­тоты. Отсюда энергия ч-цы



Разные типы резонансных циклич. У. различаются зависимостью от времени _у и < В>. При увеличении энергии ч-цы нужно либо уменьшать частоту _у (фазотрон), либо увеличивать магн. поле <B> (синхротрон), либо менять одновременно и то и другое (синхрофазотрон), либо увеличивать кратность q частоты (микротрон). Для нерелятив. скоростей масса ч-цы по­стоянна, а частота и период обращения ч-цы в постоянном магн. поле В не зависят от её скорости, и если  кратна частоте ускоряющего напряжения, мо­жет соблюдаться длит. резонанс меж­ду обращением ч-ц в магн. поле и изме­нением ускоряющего напряжения (ци­клотрон).

Фокусировка. В резонансных цик­лич. У. магн. поле В, заворачивающее ч-цы по круговой орбите, используется и для фокусировки. Если В убывает с увеличением радиуса, то силовые ли­нии имеют бочкообразную форму. Сила