Увеличение оптическое

Вид материала

Документы

Содержание Упругая деформация Поглощение звука). Упругий гистерезис Упругопластическая волна Упругости теория А. А. Ильюшин, В. С. Ленский. Шариковая модель элем. ячейки кубич. кристалла: а — в равновесии при отсутствии внеш. сил; б — под действием внеш. каса­тельного А. Н. Орлов.

Подобный материал:

• Оптическое оборудование, 171.18kb.
• Хованскова Инна Александровна, 37.43kb.
• Полиграфический словарь, 499.28kb.
• Увеличение продаж – возможно ли это сейчас?, 24.11kb.
• Оптическое оборудование, 440.32kb.
• Машиностроение, 219.74kb.
• Кроэкономической ситуации стало сохранение и увеличение денежных сбережений населения,, 61.54kb.
• Патофизиология регионарного кровообращения и микроциркуляции, 124.19kb.
• Увеличение пенсионного возраста для женщин, 218.59kb.
• Федеральная целевая программа «Жилище» на 2002-2010 годы и входящие в ее состав подпрограммы, 116.2kb.

УПРОЧНЕНИЕ металлов, повышение сопротивляемости металлов и сплавов пластич. деформации или разрушению в результате затруднения движения дислокаций и их размножения. У. явл. процессом повышения предела теку­чести при пластич. деформации.

УПРУГАЯ ДЕФОРМАЦИЯ, см. Деформация механическая.

УПРУГИЕ ВОЛНЫ, упругие возму­щения, распространяющиеся в твёр­дой, жидкой и газообразной средах, напр. волны, возникающие в земной коре при землетрясениях, звук. и ультразвук. волны в жидкостях, газах и тв. телах. При распространении У. в. в среде возникают механич. де­формации сжатия и сдвига, к-рые переносятся волной из одной точки среды в другую. При этом имеет место перенос энергии упругой деформации в отсутствие потока в-ва (исключая особые случаи, напр. акустические течения). Всякая гармонич. У. в. ха­рактеризуется амплитудой колеба­тельного смещения частиц среды и его направлением, колебательной скоро­стью частиц, переменным механич. напряжением и деформацией (к-рые в общем случае явл. тензорными ве­личинами), частотой колебаний ч-ц среды, длиной волны, фазовой и груп­повой скоростями, а также законом распределения смещений и напряже­ний по фронту волны.

В жидкостях и газах, к-рые облада­ют упругостью объёма, но не обладают упругостью формы, могут распро­страняться лишь продольные волны разрежения-сжатия, где колебания ч-ц среды происходят в направлении рас­пространения волны. Фазовая ско­рость их c_l=(K/), где К — модуль всестороннего сжатия,  — плотность среды. Пример таких У. в.— звук. волны.

В однородной изотропной бесконеч­но протяжённой тв. среде могут рас­пространяться У. в. только двух ти­пов — продольные и сдвиговые. В продольных движение ч-ц параллель­но направлению распространения вол­ны, а деформация представляет собой комбинацию всестороннего сжатия (растяжения) и чистого сдвига. В сдви­говых волнах движение ч-ц перпендику­лярно направлению распространения волны, а деформация явл. чистым сдви­гом. В безграничной среде распростра­няются продольные и сдвиговые волны трёх типов — плоские, сферические и цилиндрические. Их особенность — не­зависимость фазовой и групповой ско­ростей от амплитуды и геометрии вол­ны. Фазовая скорость продольных волн в неограниченной тв. среде сl=((К+⁴/₃G)/), сдвиговых c_t=(G/) (G — модуль сдвига). Величины c_l и с_t для разных сред колеблются в пре­делах от сотен до неск. тысяч м/с.

На границе тв. полупространства с вакуумом, газом, жидкостью или с др. тв. полупространством могут рас­пространяться упругие поверхностные волны (см. Поверхностные акустиче­ские волны), являющиеся комбинацией неоднородных продольных и сдвиговых волн, амплитуды к-рых экспоненци­ально убывают при удалении от гра­ницы.

В ограниченных тв. телах (пластина, стержень), представляющих собой тв. волноводы акустические, могут распро­страняться только нормальные волны, каждая из к-рых явл. комбинацией неск. продольных и сдвиговых волн, распространяющихся под острыми уг­лами к оси волновода и удовлетворяю­щих граничным условиям: отсутствию механич. напряжений на поверхности волновода. Число n норм. волн в пластине или стержне определяется толщиной или диаметром d, частотой  и модулями упругости среды. При уве­личении d число норм. волн возрас­тает, и при d n. Норм. волны характеризуются дисперсией фазовой и групповой скорости (см. Дисперсия звука).

В бесконечной пластине существуют два типа норм. волн — Лэмба волны и сдвиговые волны. Плоская волна Лэмба характеризуется двумя состав­ляющими смещений, одна из к-рых параллельна направлению распро­странения волны, другая — перпенди­кулярна граням пластины. В плоской сдвиговой норм. волне смещения па­раллельны граням пластины и одно­временно перпендикулярны направ­лению распространения волны. В ци­линдрич. стержнях могут распростра­няться норм. волны трёх типов — продольные, изгибные и крутильные.

В анизотропных средах (кристал­лах) св-ва У. в. зависят от типа кри­сталла и направления распростране­ния. В частности, чисто продольные и чисто сдвиговые волны могут рас­пространяться только в кристаллах определ. симметрии и по определ. на­правлениям, как правило, совпадаю­щим с направлением кристаллографич. осей. В общем случае в кристалле по

любому направлению всегда распро­страняются три волны с тремя разл. скоростями: одна квазипродольная и две квазипоперечные, в к-рых преоб­ладают соотв. продольные или попе­речные смещения (см. Кристаллоакустика). При распространении У. в. в кристаллах может возникнуть ряд специфич. эффектов, напр. различие в направлениях фазовой и групповой скорости, усиление УЗ за счёт акустоэлектронного взаимодействия, дислока­ционное поглощение.

В любой упругой среде из-за внутр. трения и теплопроводности распро­странение У. в. сопровождается её поглощением (см. Поглощение звука). Если на пути У. в. имеется к.-л. пре­пятствие (отражающая стенка, вакуум­ная полость и т. д.), то происходит дифракция волн на этом препятствии. Простейший случай дифракции — от­ражение и прохождение У. в. на пло­ской границе двух полупространств.

В У. в. механич. напряжения про­порц. деформациям (Гука закон). Если амплитуда деформации в тв. теле пре­восходит предел упругости материала, в волне появляются пластич. деформа­ции и её наз. упругопластич. волной. Аналогом таких волн в жидкостях и газах являются волны т. н. конечной амплитуды. Скорость их распростра­нения зависит от величины деформа­ции.

Диапазон частот У. в. простирается от малых долей Гц до 10¹³ Гц. В послед­нем случае длины У. в. становятся сравнимыми с параметрами крист. ре­шётки и их можно рассматривать как фононы. Область применения У. в. чрезвычайно широка: низкочастотные У. в. используются в сейсмологии (для регистрации землетрясений) и в сейс­моразведке. У. в. килогерцевого диа­пазона применяются в гидролокации и при исследованиях океана. У. в. ультра- и гиперзвук. диапазона ис­пользуются в физике для определения разл. параметров твёрдых, жидких и газообразных сред, применяются в акустоэлектронике, в промышленности для технол. и контрольно-измерит. целей, в медицине и др. областях. См. также Гиперзвук, Ультразвук.

• Ландау Л.Д., Лифшиц Е.М., Теория упругости, 3 изд., М., 1965 (Теоре­тическая физика, т. 7); Кольский Г., Волны напряжения в твердых телах, пер. с англ., М., 1955; Бергман Л., Ультра­звук и его применение в науке и технике, пер. с нем., 2 изд., М., 1957; Физическая акустика, под ред. У. Мэзона, пер. с англ., т. 1,ч. А, М., 1966, гл. 1—2, 6; т. 4, ч. А, М., 1969, гл. 1; Бреховских Л. М., Волны в слоистых средах, 2 изд., М., 1973, гл. 1; Викторов И. А., Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике, М., 1966.

И. А. Викторов.

УПРУГИЙ ГИСТЕРЕЗИС, см. Гисте­резис.

УПРУГОЕ РАССЕЯНИЕ микрочастиц, процесс столкновения (рассеяния) ч-ц, при к-ром их внутр. состояния оста-

787


ются неизменными, а меняются лишь импульсы. См. Рассеяние микрочастиц. УПРУГОПЛАСТИЧЕСКАЯ ВОЛНА, волна в деформируемом тв. теле, ам­плитуда деформации при прохождении к-рой превосходит предел упругости вещества, и возникают пласти­ческие деформации. Скорость рас­пространения таких волн зависит от величины деформации. В стержне, по к-рому прошла У. в., сохраняются остаточные деформации; по их распре­делению можно судить о динамиче­ских механических хар-ках мате­риала.

УПРУГОСТИ ТЕОРИЯ, раздел механики, в к-ром изучаются переме­щения, деформации и напряжения, возникающие в покоящихся или дви­жущихся упругих телах под действием нагрузки. У. т.— теоретич. основа расчётов на прочность, деформируе­мость и устойчивость в строит. деле, авиа- и ракетостроении, машинострое­нии, горном деле и др. областях техни­ки и пром-сти, а также в физике, сейсмологии, биомеханике и др. нау­ках. Объектами исследования метода­ми У. т. являются разнообразные тела (машины, сооружения, конструкции и их элементы, горные массивы, пло­тины, геол. структуры, части живого организма и т. п.), находящиеся под действием сил, температурных полей, радиоактивных облучений и др. воз­действий. В результате расчётов мето­дами У. т. определяются: допустимые нагрузки, при к-рых в рассчитываемом объекте не возникают напряжения или перемещения, опасные с точки зре­ния прочности или недопустимые по условиям функционирования; наибо­лее целесообразные конфигурации и размеры сооружений, конструкций и их деталей; перегрузки, возникающие при динамич. воздействии, напр. при прохождении упругих волн; амплиту­ды и частоты колебаний конструкций или их частей и возникающие в них динамич. напряжения; усилия, при к-рых рассчитываемый объект теряет устойчивость. Этими расчётами опре­деляются также материалы, наиболее подходящие для изготовления проек­тируемого объекта, или материалы, к-рыми можно заменить части организ­ма (костные и мышечные ткани, крове­носные сосуды и т. п.). Методы У. т. эффективно используются и для ре­шения нек-рых классов задач плас­тичности теории (в методе последоват. приближений).

Законы упругости, имеющие место для большинства материалов, по край­ней мере при малых (а иногда и боль­ших) деформациях, отражают взаимно однозначные зависимости между теку­щими (мгновенными) значениями на­пряжений и деформаций. Осн. физ. закон У. т.— обобщённый Гука закон, согласно к-рому напряжения линейно зависят от деформаций. Для изотропных материалов эти зависимости имеют вид:



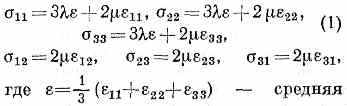
(гидростатическая) деформация,  и  — постоянные Ламе. Т. о., упругие свойства изотропного материала ха­рактеризуются двумя постоянными  и  или к.-н. выраженными через них двумя модулями упругости,

Равенство (1) можно также предста­вить в виде:



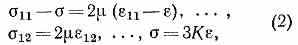
где =¹/₃(₁₁+₂₂+₃₃) — среднее

(гидростатич.) напряжение, К — мо­дуль объёмной упругости.

Для нелинейного упругого изотроп­ного материала в равенствах (2) всюду вместо  входит коэфф. Ф(_u)/3_u, а соотношение =3K заменяется ра­венством =f(), где величина _u наз. интенсивностью деформации, а функ­ции Ф и f, универсальные для данного материала, определяются из опытов. Когда Ф(_u) достигает нек-рого кри­тич. значения, возникают пластич. де­формации.

Матем. задача У. т. при равновесии состоит в том, чтобы, зная действую­щие внеш. силы (нагрузки) и т. н. граничные условия, определить в лю­бой точке тела значения компонентов тензоров напряжений и деформаций, а также компоненты u_х, u_у, u_z вектора перемещения частицы тела, т. е. опре­делить эти 15 величин в виде функций от координат х, у, z точек тела. Исход­ными для решения этой задачи яв­ляются дифференциальные ур-ния равновесия:



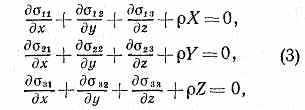
где  — плотность материала, X, Y, Z — проекции на координатные оси действующей на каждую частицу тела массовой силы (напр., силы тяжести), отнесённой к массе этой частицы. К трём ур-ниям равновесия присо­единяются 6 равенств (1) в случае изотропного тела и ещё 6 равенств вида:



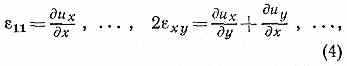
устанавливающих зависимости между компонентами деформаций и переме­щений.

Когда на часть S₁ граничной по­верхности тела действуют заданные поверхностные силы (напр., силы кон­тактного взаимодействия), проекции

к-рых, отнесённые к единице площади, равны F_x, F_y, F_z, а для части S₂ этой поверхности заданы перемещения ее точек _х, _у, _z, граничные условия имеют вид:

₁₁l₁+_l2l₂ + ₁₃l₃=F_x, (5)

u_х=_х. u_y=_y, u_z=_z, (6)

где l₁, l₂, l₃ — косинусы углов между нормалью к поверхности и координат­ными осями. Первые условия означа­ют, что искомые напряжения должны удовлетворять на границе S₁ трём равенствам (5), а вторые — что иско­мые перемещения должны удовлетво­рять на границе S₂ равенствам (6); в частном случае может быть _х=_y=_z=0 (часть поверхности S₂ жёстко закреплена). Напр., в задаче о равновесии плотины массовая сила — сила тяжести, поверхность S₂ подошвы плотины неподвижна, на остальной поверхности S₁ действуют силы: напор воды, давление разл. надстроек, трансп. средств и т. д.

В общем случае поставленная задача представляет собой пространств. зада­чу У. т., решение к-рой трудно осу­ществимо. Точные аналитич. решения имеются лишь для нек-рых частных задач: об изгибе и кручении бруса, о контактном взаимодействии двух тел, о концентрации напряжений, о дейст­вии силы на вершину конич. тела и др. Т. к. ур-ния У. т. являются линей­ными, то решение задачи о совместном действии двух систем сил получается путём суммирования решений для каждой из систем сил, действующих раздельно (принцип суперпозиции). В частности, если для к.-н. тела най­дено решение при действии сосредото­ченной силы в к.-л. произвольной точке тела, то решение задачи при произ­вольном распределении нагрузок по­лучается путём суммирования (интег­рирования). Такие решения получены лишь для небольшого числа тел (не­ограниченное пространство, полупро­странство, ограниченное плоскостью, и нек-рые др.). Предложен ряд ана­литич. методов решения пространст­венной задачи У. т.: вариационные ме­тоды (Ритца, Бубнова — Галёркина, Кастильяно и др.), метод упругих по­тенциалов, метод Бетти и др. Интен­сивно разрабатываются численные ме­тоды (конечно-разностные, метод ко­нечных элементов и др.). Разработка общих методов решений пространст­венной задачи У. т.— одна из наиболее актуальных проблем У. т.

При решении плоских задач У. т. (когда один из компонентов перемеще­ния равен нулю, а два др. зависят только от двух координат) широкое применение находят -методы теории функций комплексного переменного. Для стержней, пластин и оболочек, часто используемых в технике, най­дены приближённые решения мн.

788


практически важных задач на основе нек-рых упрощающих предположений. Применительно к этим объектам инте­рес представляют задачи об устойчиво­сти равновесия (см. Устойчивость уп­ругих систем).

В задаче термоупругости определя­ются напряжения и деформации, воз­никающие вследствие неоднородного распределения темп-ры в теле. При матем. постановке этой задачи в пра­вую часть первых трёх ур-ний (1) добавляется член -(З+2)T, где  — коэфф. линейного теплового рас­ширения, Т (х₁, х₂, х₃) — заданное поле темп-ры. Аналогичным образом строится теория электромагнитоупругости и упругости тел, подвергаемых облучению.

Большой практич. интерес пред­ставляют задачи У. т. для неоднород­ных тел. В этих задачах коэфф.  и  в ур-нии (1) являются не константами, а функциями координат, определяю­щими поле упругих свойств тела, к-рое иногда задают статистически (в виде нек-рых функций распределения). Применительно к этим задачам разра­батываются статистич. методы У. т., отражающие статистическую природу свойств поликристаллич. тел.

В динамич. задачах У. т. искомые величины являются функциями коор­динат и времени. Исходными для матем. решения этих задач являются дифф. ур-ния движения, отличающие­ся от ур-ний (3) тем, что правые части вместо нуля содержат инерц. члены д²u_x/дt² и т. д. К исходным ур-ниям должны также присоединяться ур-ния (1), (4) и, кроме граничных условий (5), (6), ещё задаваться начальные ус­ловия, определяющие, напр., распре­деление перемещений и скоростей ч-ц тела в начальный момент времени. К этому типу относятся задачи о коле­баниях конструкций и сооружений, в к-рых могут определяться формы коле­баний и их возможные смены, ампли­туды колебаний и их нарастание или убывание во времени, резонансные ре­жимы, динамич. напряжения, методы возбуждения и гашения колебаний и др., а также задачи о распростране­нии упругих волн (сейсмич. волны и их воздействие на конструкции и со­оружения, волны, возникающие при взрывах и ударах, термоупругие вол­ны и т. д.).

Одной из совр. проблем У. т. яв­ляется матем. постановка задач и раз­работка методов их решения при ко­нечных (больших) упругих деформа­циях.

Экспериментальные методы У. т. (метод многоточечного тензометрирования, поляризационно-оптический ме­тод исследования напряжений, метод муаров и др.) позволяют в нек-рых случаях непосредственно определить распределение напряжений и дефор­маций в исследуемом объекте или на его поверхности. Эти методы исполь­зуются также для контроля решений, полученных аналитич. и численными

методами, особенно когда решения найдены при к.-н. упрощающих допу­щениях. Иногда эффективными оказы­ваются экспериментально-теоретич. ме­тоды, в к-рых частичная информация об искомых функциях получается из опытов.

• Ляв А. (Л а в), Математическая теория упругости, пер. с англ., М.— Л., 1935; Трехмерные задачи математической теории упругости и термоупругости, под ред. В. Д. Купрадзе, 2 изд., М., 1976;

С т р е т т Дж. В. (лорд Рэлей), Теория звука, пер. с англ., 2 изд., т. 1—2, М., 1955; Боли Б. Уэйнер Дж., Теория температурных напряжений, пер. с англ., М., 1964; Т и м о ш е н к о С. П., Гудьер Дж. Н., Теория упругости, пер. с англ., М., 1975.

А. А. Ильюшин, В. С. Ленский.

УПРУГОСТЬ, свойство тел изменять форму и размеры под действием на­грузок и самопроизвольно восстанав­ливать исходную конфигурацию при прекращении внеш. воздействий.

Количественно У. выражается в том, что компоненты тензора напряжений (см. Напряжение механическое) в изотермич. условиях явл. функциями ком­понентов тензора деформации (см. Де­формация механическая), к-рые уни­версальны для данного материала и не зависят от того, в каком порядке про­исходит изменение разл. компонентов деформации до достижения ими рас­сматриваемых значений. В большин­стве материалов (напр., в металлах, керамике, горных породах, древесине) при малых деформациях зависимости между напряжениями и деформациями можно считать линейными и описы­вать обобщённым Гука законом. Зако­нам нелинейной У. можно придать форму, подобную обобщённому закону Гука, заменив модули упругости нек-рыми универсальными функци­ями (см. Упругости теория).

У. тел обусловлена силами вз-ствия атомов, из к-рых они построены. В тв. телах при темп-ре абс. нуля в отсутст­вии внеш. напряжений атомы занима­ют равновесные положения, в к-рых сумма всех сил, действующих на каж­дый атом со стороны остальных, равна нулю, а потенц. энергия атома мини­мальна. Кроме сил притяжения и от­талкивания, зависящих только от рас­стояния между атомами (центр. силы), в многоатомных молекулах и макро­скопич. телах действуют также не­центральные силы, зависящие от т. н. валентных углов между прямыми, со­единяющими данный атом с разл. его соседями (рис.). При равновесных значениях валентных углов нецент­ральные силы также уравновешены. Энергия макроскопич. тела зависит от межатомных расстояний и валентных углов, принимая миним. значение при равновесных значениях этих парамет­ров.

Под действием внеш. напряжений атомы смещаются из своих равновес­ных положений, что сопровождается увеличением потенц. энергии тела на величину, равную работе внеш. на­пряжений по изменению объёма и формы тела. После снятия внеш. на­пряжений конфигурация упруго де-

формиров. тела с неравновесными меж­атомными расстояниями и валентными углами оказывается неустойчивой и самопроизвольно возвращается в рав­новесное состояние. Запасённая в теле избыточная потенц. энергия превра­щается в кинетич. энергию колеблю­щихся атомов, т. е. в теплоту. Пока отклонения межатомных расстояний и



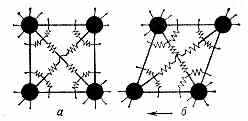
Шариковая модель элем. ячейки кубич. кристалла: а — в равновесии при отсутствии внеш. сил; б — под действием внеш. каса­тельного напряжения.


валентных углов от их равновесных значений малы, они пропорц. дейст­вующим между атомами силам, подоб­но тому, как удлинение или сжатие пружины пропорц. приложенной силе. Поэтому тело можно представить как совокупность атомов-шариков, соеди­нённых пружинами, ориентации к-рых фиксированы др. пружинами (рис.). Константы упругости этих пружин определяют модули упругости мате­риала.

В жидкости тепловые колебания имеют амплитуду, сравнимую с равно­весным межатомным расстоянием, вследствие чего атомы легко меняют своих соседей и не сопротивляются касат. напряжениям, если они прикла­дываются со скоростью, значительно меньшей скорости тепловых колеба­ний. Поэтому жидкости (как и газы) не обладают упругостью формы, а только объёма: уменьшение объёма пропорционально приложенному дав­лению.

В газообразном состоянии средние расстояния между атомами или моле­кулами значительно больше, чем в конденсированном. Упругость газов (паров) определяется тепловым дви­жением молекул, ударяющихся о стен­ки сосуда, ограничивающего объём газа.

• Фейнман Р., Лейтон Р., С э н д с М., Фейнмановские лекции по фи­зике, 2 изд., [в.] 7, М., 1977, гл. 38—39; Смирнов А. А., Молекулярно-кинетическая теория металлов, М., 1966, гл. 2; Френкель Я. И., Введение в теорию металлов, 4 изд., Л., 1972, гл. 2.

А. Н. Орлов.