Увеличение оптическое

Вид материала

Документы

Содержание Увлечения эффект В. Л. Гуревич, С. М. Рывкин. Угловая скорость Угловое ускорение Угловой момент Угол диэлектрических по­терь А к В тел (рис.), имеющих в этот момент скорость сближения vA Схема удара двух тел. Столкно­вения атомные). Ударная волна Рис. 1. Ударная адиа­бата Н и адиабата Пуассона Р, прохо­дящие через общую начальную точку А исходного состояния. H, отличается от обычной адиабаты Р Рис. 3. Распределе­ние температуры (a) и плотности (б) в ударной волне, рас­пространяющейся в реальном газе. Ю. П. Райзер. Ударная ионизация УДАРЫ ВТОРОГО РОДА (столкнове­ния второго рода, соударения второго рода) Удельная рефракция ( Удельная электропроводность Удельное магнитное враще­ние Удельный вес ... Полное содержание

Подобный материал:

• Оптическое оборудование, 171.18kb.
• Хованскова Инна Александровна, 37.43kb.
• Полиграфический словарь, 499.28kb.
• Увеличение продаж – возможно ли это сейчас?, 24.11kb.
• Оптическое оборудование, 440.32kb.
• Машиностроение, 219.74kb.
• Кроэкономической ситуации стало сохранение и увеличение денежных сбережений населения,, 61.54kb.
• Патофизиология регионарного кровообращения и микроциркуляции, 124.19kb.
• Увеличение пенсионного возраста для женщин, 218.59kb.
• Федеральная целевая программа «Жилище» на 2002-2010 годы и входящие в ее состав подпрограммы, 116.2kb.

У

УВЕЛИЧЕНИЕ ОПТИЧЕСКОЕ, от­ношение линейных или угловых раз­меров изображения предмета, получа­емого с помощью оптич. системы, к соответствующим размерам самого предмета. Характеризуя наиболее упо­требит. осесимметричные системы, различают линейное, угловое и про­дольное У. о. Линейное (попе­речное) увеличение  — отношение длины V изображения от­резка, перпендикулярного оптич. оси системы, к длине этого отрезка l: =l'/l. При >0 (направления l и l' совпадают) изображение наз. прямым, при <0 (l и V антипараллельны) — обратным или перевёрнутым, при ││<1 — уменьшенным, при ││>1 — увеличенным. Величину  оптич. системы можно вычислить, используя выражение =-f/x=-x'/f', где f и f' — переднее и заднее фокусные рас­стояния, а х и х' — расстояния от переднего фокуса до предмета и от заднего фокуса до изображения соот­ветственно. В реальных оптич. си­стемах линейное У. о. для сопряжён­ных плоскостей не остаётся постоян­ным по всему полю зрения. Это при­водит к нарушению геом. подобия между предметом и его изображением, наз. дисторсией.

Угловое увеличение  — отношение тангенса угла наклона u' луча к оптич. оси в пространстве изоб­ражений к тангенсу угла наклона и сопряжённого ему луча в простран­стве предметов: =tgu'/tgu. Про­дольное увеличение  — отношение длины отрезка x', отло­женного вдоль оптич. оси системы в пространстве изображений, к сопря­жённому ему отрезку Ах в простран­стве предметов: а=x'/x.

Величины ,  и  взаимосвязаны: =. Если n и n' — показатели пре­ломления среды в пространстве пред­метов и пространстве изображений соответственно, то =n/n'. Для оп­тич. системы, находящейся в воздухе, n=n' и =1/, т. е. угловое увели­чение обратно пропорционально ли­нейному. Это означает, что чем больше линейное увеличение, тем уже све­товые пучки, с помощью к-рых стро­ится изображение, и тем меньше его освещённость.  и  связаны выра­жением: =²n'/n, и при n=n' =². Т. к. продольное и поперечное У. о. различны, то даже идеальная оптич. система не может точно передать про­странство предметов — размеры изоб­ражения по оси сокращаются и оно становится плоским.

• Л а н д с б е р г Г. С., Оптика, 5 изд., М., 1976; Тудоровский А. И., Тео­рия оптических приборов, 2 изд., т. 1—2, М.— Л., 1948—52.

Л. Н. Капорский.

УВЛЕЧЕНИЯ ЭФФЕКТ, 1) возник­новение потока электронов в металле или полупроводнике в условиях, когда фононы не находятся в тепловом рав­новесии, а образуют направл. поток, напр. при наличии градиента темп-ры (увлечение электронов фононами). В образце, на концах к-рого создана разность темп-р, воз­никает поток фононов от более на­гретого конца к более холодному, пропорц. градиенту темп-ры. В ре­зультате столкновений электронов с фононами, к-рые передают электро­нам часть своего квазиимпульса, воз­никает электронный поток, в замкну­той цепи появляется электрич. ток (ток увлечения). Если об­разец электрически разомкнут, то в нём возникает эдс. У. э. вносит вклад в теплопроводность, термоэлектрич. и термомагн. эффекты. В отличие от акустоэлектрического эффекта элект­роны увлекаются потоком некоге­рентных фононов. У. э. теоретически исследован Л. Э. Гуревичем (1945) и экспериментально обнаружен в по­лупроводниках (1953) по аномально большому увеличению термоздс в Ge при понижении темп-ры, интерпрети­рованному как следствие У. э. У. э. используется для исследования ме­ханизмов электронной и фононной релаксации в проводниках.

2) Появление электронного потока в результате передачи импульса от направленного потока фотонов элект­ронам в твёрдом проводнике (увле­чение электронов фото­нами). У. э. наблюдается в оптич. и СВЧ областях в полупроводниках, полуметаллах (Bi) и нек-рых метал­лах. Наиболее подробно изучен в по­лупроводниках (Ge, Si, соединения типа A^IIIB^V), где происходит увле­чение связанных электронов (фото­ионизация) или электронов про­водимости и дырок. Импульс фотонов, в конечном счёте приобретаемый всем твёрдым телом, вначале в значит. мере воспринимается подвижными носите­лями, вызывая их смещение. Дли­тельность начальной стадии ~10^-12— 10^-13 с, что определяет малость эф­фекта и его малую инерционность. Т. к. импульс фотона равен сумме импульсов, приобретаемых решёткой и электроном, то возможен случай, когда импульс, приобретаемый элект­роном, противоположен по знаку им­пульсу фотона. У. э. обнаруживается в виде тока (ток увлечения) или эдс.

Плотность тока может быть записана в виде:



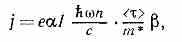
где е, m*, <> — заряд, эффектив­ная масса, и усреднённое время ре­лаксации импульса носителей; с, I, n,  — соответственно скорость, интен­сивность (в фотон/см²•с), показатель преломления, коэфф. поглощения све­та; ћ — энергия фотона;  — коэфф., характеризующий долю импульса фо­тонов, приобретаемую электронами. В полупроводниках наблюдается на­ряду с продольным т. н. поперечный У. э. (появление тока, направленного перпендикулярно импульсу фотонов). У. э. используется для измерения вре­менных характеристик излучения им­пульсных лазеров и для регистрации ИК излучения.

• Блатт Ф. Дж., Физика электрон­ной проводимости в твердых телах, пер. с англ., М., 1971.

В. Л. Гуревич, С. М. Рывкин.

УГЛЕРОДНЫЙ ЦИКЛ (CNO-цикл), последовательность термоядерных ре­акций в звёздах, приводящая к пре­вращению водорода в гелий (⁴Не) с участием углерода в качестве катали­затора. У. ц. протекает при темп-рах в недрах звёзд 18•10⁶К, когда веще­ство звезды уже содержит изотоп ¹²С:



Здесь е⁺ — позитрон,  — нейтрино, 7 — испускаемый фотон. Под реак­циями указаны их энергетич. выход (в МэВ) и продолжительность (см. Водородный цикл). При образовании одного ядра гелия путём У. ц. выде­ляется ~25 МэВ энергии, образую­щиеся нейтрино уносят ещё ок. 5% от этой величины.

• Шкловский И. С., Звезды. Их рождение, жизнь и смерть, 2 изд., М.,1977.

УГЛОВАЯ СКОРОСТЬ, векторная ве­личина, характеризующая быстроту

776


вращения твёрдого тела. При равно­мерном вращении тела вокруг непо­движной оси численно его У. с. =/t, где — приращение угла поворота  за промежуток времени t, а в общем случае =d/dt. Век­тор У. с. направлен вдоль оси враще­ния в ту сторону, откуда поворот тела виден происходящим против хода часовой стрелки (в правой системе координат). Размерность У. с. Т^-1.

УГЛОВОЕ УСКОРЕНИЕ, величина, характеризующая быстроту изменения угловой скорости твёрдого тела. При вращении тела вокруг неподвижной оси, когда его угловая скорость  растёт (или убывает) равномерно, чис­ленно У. у. =/t, где  — при­ращение, к-рое получает  за проме­жуток времени At, а в общем случае =d/dt. Вектор У. у.  направлен при этом вдоль оси вращения (в ту же сторону, что и  при ускоренном вращении и противоположно — при замедленном). При вращении вокруг неподвижной точки вектор У. у. =d/dt и направлен по касательной к годографу вектора (о в соответству­ющей его точке. Размерность У. у.

T^-2

УГЛОВОЙ МОМЕНТ, то же, что момент количества движения.

УГОЛ АТАКИ, угол между направ­лением скорости поступательно дви­жущегося тела и к.-н. характерным направлением, связанным с телом, напр. у крыла самолёта — с хордой крыла (см. рис. в ст. Центр давления), у снаряда, ракеты — с их осью сим­метрии.

УГОЛ ДИЭЛЕКТРИЧЕСКИХ ПО­ТЕРЬ, разность б фаз колебаний век­торов электрич. индукции D и напря­жённости переменного электрич. по­ля E. Характеризует диэлектрические потери в среде. Отношение энер­гии, поглощённой диэлектриком за период колебаний, к ср. энергии пере­менного электрич. поля равно 4tg. У. д. п. связан с действительной ' и мнимой " частями диэлектрической проницаемости соотношением:

tg="/'

(см. также Диэлектрики).

УДАР твёрдых тел, совокупность яв­лений, возникающих при столкнове­нии движущихся твёрдых тел, а также при нек-рых видах взаимодействия твёрдого тела с жидкостью или газом (У. струи о тело, У. тела с поверх­ностью жидкости, гидравлический удар, действие взрывной или ударной волны на твёрдое тело и др.). Про­межуток времени, в течение к-рого длится У., обычно очень мал (на практике ~10^-4—10^-5 с), а разви­вающиеся на площадках контакта соударяющихся тел силы (т. н. удар­ные или мгновенные) очень велики. За время У. они изменяются в ши­роких пределах и достигают значений, при к-рых средние величины дав­ления (напряжений) на площадках контакта имеют порядок 10⁴ и даже

10⁵ атм. Действие ударных сил при­водит к значит. изменению за время У. скоростей точек тела. Следствиями У. могут быть также остаточные де­формации, звуковые колебания, на­гревание тел, изменение механич. свойств их материалов (в частности, их упрочнение), полиморфные и хим. превращения и др., а при скоростях соударения, превышающих критиче­ские,— разрушение тел в месте У. Критич. скорости для металлов имеют порядок 15 м/с (медь) — 150 м/с и более (высококачеств. стали).

Изменение скоростей точек тела за время У. определяется методами об­щей теории У., где в качестве меры механич. взаимодействия тел при У. вместо самой ударной силы Р вво­дится её импульс за время У. т, т. е.

величина S =∫^₀Pdt=P_cp, наз.

ударным импульсом. Од­новременно, ввиду малости т, импуль­сами всех неударных сил, таких, напр., как сила тяжести, а также перемещениями точек тела за время У. пренебрегают. Осн. ур-ния общей теории У. вытекают из теорем об из­менении количества движения и ки­нетич. момента системы при У. С по­мощью этих теорем, зная приложен­ный ударный импульс и скорости в начале У., определяют скорости в конце У., а если тело является не­свободным, то и импульсивные ре­акции связей.

Процесс соударения двух тел можно разделить на две фазы. 1-я фаза на­чинается с момента соприкосновения точек А к В тел (рис.), имеющих в этот момент скорость сближения vA_n-vB_n, где vA_n и vB_n— проекции скоростейv_A и v_B на общую нормаль n к поверхности тел в точках А и В, наз. лини­ей удара. К концу 1-й фазы сближение тел пре­кращается, а часть их кинетич. энер­гии переходит в потенц. энергию де­формации.



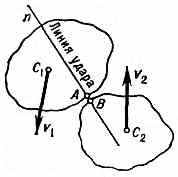
Схема удара двух тел.


Во 2-й фазе происходит обратный переход потенц. энергии упругой деформации в кинетич. энер­гию тел; при этом тела начинают рас­ходиться и к концу 2-й фазы точки А и В будут иметь скорость расхож­дения V_An-V_Bn. Для совершенно упругих тел механич. энергия к концу У. восстановилась бы полностью и было бы |V_An-V_Bn|=|v_An-v_Bn|; наоборот, У. совершенно неупругих тел закончился бы на 1-й фазе (V_An-V_Bn=0). При У. реальных тел ме­ханич. энергия к концу У. восста­навливается лишь частично вслед­ствие потерь на образование оста­точных деформаций, нагревание тел и др.: |V_An-V_Bn|<|v_An-v_Bn|.

Для учёта этих потерь вводится т. н. коэфф. восстановления k, к-рый счи тается зависящим только от физ. свойств материалов тел:

k=|V_An-V_Bn|/|v_An-v_Bn|=- (V_An-V_Bn)/(v_An-v_Bn).

В случае У. по неподвижному телу V_Bn=v_Bn=0 и k=-V_An/v_An. Зна­чение k определяется эксперимен­тально, напр. измерением высоты h, на к-рую отскакивает шарик, сво­бодно падающий на горизонт. плиту из того же материала, что и шарик, с высоты H; в этом случае k=(h/H). По данным опытов, при соударении тел из дерева k0,5, из стали — 0,55, из слоновой кости — 0,89, из стек­ла — 0,94. В предельных случаях при совершенно упругом У. k=1, a при совершенно не упругом k=0. Зная скорости в начале У. и коэфф. k, можно найти скорости в конце У. и действующий в точках соударения ударный импульс S.

Если центры масс тел С₁ и С₂ лежат на линии У., то У. наз. централь­ным (У. шаров); в противном слу­чае -- нецентральным. Если скорости v₁ и v₂ центров масс в на­чале У. направлены параллельно ли­нии У., то У. наз. прямым; в про­тивном случае — косым. При пря­мом центральном У. двух гладких тел (шаров) 1 и 2



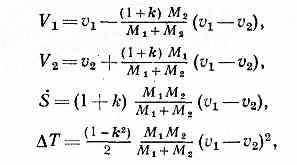
где T — потерянная за время У. кинетич. энергия системы, М₁ и М₂ — массы шаров. В частном случае при k=1 и М₁=М₂ получается V₁=v₂ и V₂=v₁, т. е. шары одинаковой массы при совершенно упругом У. обмениваются скоростями; при этом T=0.

Для определения времени У., удар­ных сил и вызванных ими в телах напряжений и деформаций необхо­димо учесть механич. свойства мате­риалов тел и изменения этих свойств за время У., а также характер на­чальных и граничных условий. Ре­шение проблемы существенно услож­няется не только из-за трудностей чисто матем. характера, но и ввиду отсутствия достаточных данных о па­раметрах, определяющих поведение материалов тел при ударных нагруз­ках, что заставляет делать при рас­чётах ряд существенных упрощающих предположений. Наиболее разрабо­тана теория У. совершенно упругих тел, в к-рой предполагается, что тела за время У. подчиняются законам упругого деформирования (см. Упру­гости теория) и в них не появляется.

777


остаточных деформаций. Деформация, возникшая в месте контакта, распро­страняется в таком теле в виде уп­ругих волн со скоростью, зависящей от физ. свойств материала. Если время прохождения этих волн через всё тело много меньше времени У., то влиянием упругих колебаний можно пренебречь и считать характер кон­тактных взаимодействий при У. таким же, как в статич. состоянии. На таких допущениях основывается контактная теория удара Г. Герца. Если же время прохождения упругих волн через тело сравнимо со временем У., то для расчётов пользуются волновой теорией У.

Изучение У. не вполне упругих тел — задача значительно более слож­ная, требующая учёта как упругих, так и пластич. свойств материалов. При решении этой задачи и связанных с ней проблем определения механич. свойств материалов тел при У., изу­чения изменений их структуры и про­цессов разрушения широко опираются. на анализ и обобщение результатов многочисл. эксперимент. исследова­ний. Экспериментально исследуются также специфич. особенности У. тел при больших скоростях (~ сотен м/с) и при воздействии взрыва, к-рый в случае непосредств. контакта заряда с телом можно считать эквивалентным соударению со скоростью до 1000 м/с.

Кроме У. твёрдых тел, в физике изучают столкновения молекул, ато­мов и элементарных ч-ц (см. Столкно­вения атомные).

• Кильчевский Н. А., Теория соударений твердых тел, К., 1969; Д и н н и к А. Н., Удар и сжатие упругих тел, К., 1952 (Избр. труды, т. 1); Д а в и д е н к о в Н. Н., Динамические испытания ме­таллов, 2 изд., Л.— М., 1936; Илью­шин А. А., Ленский В. С., Сопротив­ление материалов, М., 1959, гл. 6; Р а й н х а р т Дж., П и р с о н Дж., Поведение металлов при импульсивных нагрузках, пер. с англ., М., 1958.

С. М. Тарг.

УДАРНАЯ ВОЛНА (скачок уплотне­ния), распространяющаяся со сверх­звуковой скоростью тонкая переход­ная область, в к-рой происходит рез­кое увеличение плотности, давления и скорости в-ва. У. в. возникают при взрывах, детонации, при сверхзву­ковых движениях тел, при мощных электрич. разрядах и т. д. Напр., при взрыве ВВ образуются высоконагре­тые продукты взрыва, обладающие большой плотностью и находящиеся под высоким давлением. В нач. мо­мент они окружены покоящимся воз­духом при норм. плотности и атм. давлении. Расширяющиеся продукты взрыва сжимают окружающий воз­дух, причём в каждый момент времени сжатым оказывается лишь воздух, находящийся в определённом объёме; вне этого объёма воздух остаётся в невозмущённом состоянии. С тече­нием времени объём сжатого воздуха возрастает. Поверхность, к-рая отделяет сжатый воздух от невозмущён­ного, и представляет собой У. в. (или, как говорят, фронт У. в.). В ряде случаев сверхзвукового дви­жения тел в газе (артиллерийские снаряды, спускаемые космич. аппа­раты) направление движения газа не совпадает с нормалью к поверхности фронта У. в., и тогда возникают косые У. в. (см. Сверхзвуковое течение).

Примером возникновения и рас­пространения У. в. может служить сжатие газа в трубе поршнем. Если поршень вдвигается в газ медленно, то по газу со скоростью звука а бежит акустич. (упругая) волна сжа­тия. Если же скорость поршня не мала по сравнению со скоростью звука, возникает У. в., скорость рас­пространения к-рой по невозмущён­ному газу больше, чем скорость дви­жения ч-ц газа (т. н. массовая ско­рость), совпадающая со скоростью поршня. Расстояния между ч-цами в У. в. меньше, чем в невозмущён­ном газе, вследствие сжатия газа. Если поршень сначала вдвигают в газ с небольшой скоростью и постепенно ускоряют, то У. в: образуется не сразу. Вначале возникает волна сжа­тия с непрерывными распределениями плотности  и давления р. С течением времени крутизна передней части вол­ны сжатия нарастает, т. к. возмуще­ния от ускоренно движущегося порш­ня догоняют её и усиливают, вслед­ствие чего возникает резкий скачок всех гидродинамич. величин, т. е. У. в.

Законы ударного сжа­тия. При прохождении газа через У. в. его параметры меняются очень резко и в очень узкой области. Тол­щина фронта У. в. имеет порядок длины свободного пробега молекул, однако при многих теоретич. иссле­дованиях можно пренебречь столь малой толщиной и с большой точно­стью заменить фронт У. в. поверх­ностью разрыва, считая, что при прохождении через неё параметры газа изменяются скачком (отсюда назв. «скачок уплотнения»). Значения пара­метров газа по обе стороны скачка связаны след. соотношениями, выте­кающими из законов сохранения мас­сы, импульса и энергии:

₁v₁ =₀v₀, р₁+p₁v²₁ =p₀+₀v²₀, ₁+p₁/₁ +v²₁/2=₀+ p₀/₀+v²₀/2, (1)

где p₁ — давление, ₁ — плотность, ξ₁ — удельная внутр. энергия, v₁ — скорость в-ва за фронтом У. в. (в системе координат, в к-рой У. в. покоится), а р₀, ₀, ξ₀, v₀ — те же величины перед фронтом. Скорость v_о втекания газа в разрыв численно совпадает со скоростью распростра­нения У. в. v_b по невозмущённому газу. Исключая из равенств (1) ско­рости, можно получить ур-ния удар­ной адиабаты:

ξ₁-ξ₀=¹/₂(p₁+p₀)(V₀-V₁), w₁-w₀=¹/₂ (p₁ -p₀) (V₀+V₁), (2)

где V=1/ — удельный объём, w=ξ+p/ — удельная энтальпия. Если известны термодинамич. свойства в-ва, т. е. функции ξ(p, ) или w(p, ), то ударная адиабата даёт зависимость конечного давления p₁ от конечного объёма V₁ при ударном сжатии в-ва из данного нач. состояния р₀, V₀, т. е. зависимость p₁=H(V₁, p₀, V₀).

При переходе через У. в. энтропия в-ва S меняется, причём скачок энт­ропии S₁-S₀ для данного в-ва оп­ределяется только законами сохра­нения (1), к-рые допускают сущест­вование двух режимов: скачка сжатия (₁>₀, p₁>p₀) и скачка разрежения (₁<₀, p_1
0). Однако в соответствии со вторым началом термодинамики ре­ально осуществляется только тот ре­жим, при к-ром энтропия возрастает. В обычных в-вах энтропия возрастает только в У. в. сжатия, поэтому У. в. разрежения не реализуется (теорема Цемплена).

У. в. распространяется по невозму­щённому в-ву со сверхзвуковой ско­ростью v₀>а₀ (где a₀ — скорость звука в невозмущённом в-ве), тем большей, чем больше интенсивность У. в., т. е. чем больше (p₁-p₀)/p₀. При стрем­лении интенсивности У. в. к 0 ско­рость её распространения стремится к а₀. Скорость У. в. относительно сжатого газа, находящегося за ней, является дозвуковой:v₁1 (а₁ — скорость звука в сжатом газе за У. в.).

У. в. в идеальном газе с постоянно и теплоёмко­стью. Это наиболее простой случай распространения У. в., т. к. ур-ние состояния имеет предельно простой вид: =p/(-1), p=RT/, где =с_p/с_v — отношение теплоёмкостей при постоянных давлении и объёме



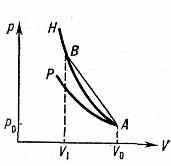
Рис. 1. Ударная адиа­бата Н и адиабата Пуассона Р, прохо­дящие через общую начальную точку А исходного состояния.


(т. н. показатель адиабаты), R — универсальная газовая постоянная, (1 — молекулярная масса. Ур-ние ударной адиабаты можно получить в явном виде:



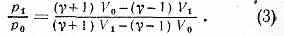
Ударная адиабата, или ади­абата Гюгоньо H, отличается от обычной адиабаты Р (адиабаты Пу­ассона), для к-рой p₁/p₀=(V₀/V₁) (рис. 1). При ударном сжатии в-ва для данного изменения V необходимо большее изменение р, чем при адиабатич. сжатии. Это является следст­вием необратимости нагревания при ударном сжатии, связанного, в свою

778


очередь, с переходом в теплоту кине­тич. энергии потока, набегающего на фронт У. в. В силу соотношения v²₀=V²₀(p₁-p₀)/(V₀-V₁), следующего из ур-ния (1), скорость У. в. опреде­ляется наклоном прямой А В, соеди­няющей точки начального и конечного состояний.

Связь параметров газа в У. в. можно Представить в зависимости от Маха числа М=v_в/a₀:



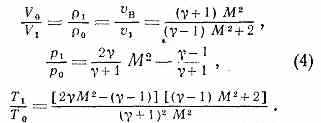
В пределе для сильных У. в. при М, p₁/p₀ получается:



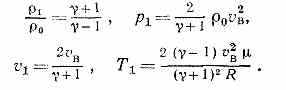
Т. о., сколь угодно сильная У. в. не может сжать газ более чем в {+1)/(-1) раз. Напр., для одноатом­ного газа = ⁵/₃ и предельное сжатие равно 4, а для двухатомного (напр., воздуха) =⁷/₅ и предельное •сжатие равно 6. Предельное сжатие тем выше, чем больше теплоёмкость газа (меньше ).

Вязкий скачок уплотнения. Необратимость ударного сжа­тия свидетельствует о наличии дис­сипации механич. энергии во фронте У. в. Диссипативные процессы можно учесть, приняв во внимание вязкость и теплопроводность газа. При этом оказывается, что сам скачок энтропии в У. в. не зависит ни от механизма диссипации, ни от вязкости и тепло­проводности газа.



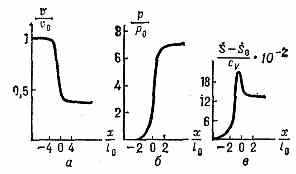
Рис. 2. Распределение скорости (а), давле­ния (б) и энтропии (в) в вязком скачке уп­лотнения с числом М=2 в газе; х — коор­дината, нормальная к фронту ударной вол­ны, l₀ — длина свободного пробега моле­кул в невозмущённом газе.


Последние определя­ют лишь внутреннюю структуру фрон­та волны и его толщину. В У. в. не •слишком большой интенсивности все величины — v, р,  и Т монотонно изменяются от своих начальных до конечных значений (рис. 2). Энтропия же S меняется немонотонно и внутри У. в. достигает максимума в точке перегиба скорости, т. е. в центре волны (х=0). Возникновение мак­симума S в волне связано с сущест­вованием теплопроводности. Вязкость

приводит только к возрастанию энт­ропии, т. к. благодаря ей происходит рассеяние импульса направленного газового потока, набегающего на У. в., и превращение кинетич. энергии на­правленного движения в энергию хаотич. движения, т. е. в теплоту. Бла­годаря же теплопроводности теплота необратимым образом перекачивается из более нагретых слоев газа в менее нагретые.

У. в. в реальных газах. В реальном газе при высоких темп-рах происходят возбуждение молекуляр­ных колебаний, диссоциация молекул, хим. реакции, ионизация и т. д., что связано с затратами энергии и из­менением числа ч-ц. При этом внутр. энергия  сложным образом зависит от p и  и параметры газа за фронтом У. в. можно определить только чис­ленными расчётами по ур-ниям (1), (2).

Для перераспределения энергии га­за, сжатого и нагретого в сильном скачке уплотнения, по различным степеням свободы требуется обычно очень много соударений молекул. Поэтому ширина слоя x, в к-ром происходит переход из начального в конечное термодинамически равно­весное состояние, т. е. ширина фронта У. в., в реальных газах обычно го­раздо больше ширины вязкого скачка и определяется временем релаксации наиболее медленного из процессов: возбуждения колебаний, диссоциации, ионизации и т. д. Распределения



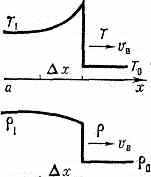
Рис. 3. Распределе­ние температуры (a) и плотности (б) в ударной волне, рас­пространяющейся в реальном газе.


темп-ры и плотности в У. в. при этом имеют вид, показанный на рис. 3, где вязкий скачок уплотнения изоб­ражён в виде взрыва.

В У. в., за фронтом к-рых газ сильно ионизован или к-рые распро­страняются по плазме, ионная и электронная темп-ры не совпадают. В скачке уплотнения нагреваются только тяжёлые ч-цы, но не электро­ны, а обмен энергии между ионами и электронами происходит медленно вследствие большого различия их масс. Релаксация связана с выравни­ванием темп-р. Кроме того, при рас­пространении У. в. в плазме существ. роль играет электронная теплопро­водность, к-рая гораздо больше ион­ной и благодаря к-рой электроны про­греваются перед скачком уплотнения. В электропроводной среде в присут­ствии внеш. магн. поля распростра­няются магнитогидродинамич. У. в.

Их теория строится на основе ур-ний магнитной гидродинамики аналогично теории обычных У. в.

При темп-рах выше неск. десятков тыс. градусов на структуру У. в. существенно влияет лучистый тепло­обмен. Длины пробега световых кван­тов обычно гораздо больше газокинетич. пробегов, и именно ими опреде­ляется толщина фронта. Все газы непрозрачны в более или менее далё­кой ультрафиолетовой области спект­ра, поэтому высокотемпературное из­лучение, выходящее из-за скачка уп­лотнения, поглощается перед скачком и прогревает несжатый газ. За скач­ком газ охлаждается за счёт потерь на излучение. В этом случае ширина фронта — порядка длины пробега из­лучения (~10²—10^-1 см в воздухе норм. плотности). Чем выше темп-ра за фронтом, тем больше поток излу­чения с поверхности скачка и тем выше темп-ра газа перед скачком. Нагретый газ перед скачком не про­пускает видимый свет, идущий из-за фронта У. в., экранируя фронт. По­этому яркостная темп-ра У. в. не всегда совпадает с истинной темп-рой за фронтом.

У. в. в твёрдых телах. Энер­гия и давление в твёрдых телах имеют двоякую природу: они связаны с теп­ловым движением и с взаимодействием ч-ц (тепловые и упругие составляю­щие). Теория междучастичных сил не может дать общей зависимости упру­гих составляющих давления и энергии от плотности в широком диапазоне для разных в-в, и, следовательно, теоре­тически нельзя построить функцию (p,). Поэтому ударные адиабаты для твёрдых (и жидких) тел опреде­ляются из опыта или полуэмпириче­ски. Для значит. сжатия твёрдых тел нужны давления в миллионы атмосфер, к-рые сейчас достигаются при экс­перимент. исследованиях. На прак­тике большое значение имеют слабые У. в. с давлениями 10⁴—10⁵ атм. Это давления, к-рые развиваются при •детонации, взрывах в воде, ударах продуктов взрыва о преграды и т. д. Повышение энтропии в У. в. с такими давлениями невелико, и для расчёта распространения У. в. обычно поль­зуются эмпирич. ур-нием состояния типа р=А[(/₀)ⁿ-1], где величина А, вообще говоря, зависящая от энтро­пии, так же, как и n, считается постоянной. В ряде в-в — железе, вис­муте и др. в У. в. происходят фазовые переходы — полиморфные превраще­ния. При небольших давлениях в твёрдых телах возникают упругие волны, распространение к-рых, как и распространение слабых волн сжа­тия в газах, можно рассматривать на основе законов акустики.

• Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред, 2 изд., М., 1953; Зельдович Я. В., Райзер Ю. П., Физика ударных волн и высокотемператур-

779


ных гидродинамических явлений, 2 изд., М., 1966; С т у п о ч е н к о Е. В., Ло­сев С. А., О с и п о в А. И., Релакса­ционные процессы в ударных волнах, М., 1965.

Ю. П. Райзер.