Урок геометрии и информатики. Тема урока по учебному плану: Построение правильных многоугольников

Есть в школьной геометрии такие темы, при изучении которых встречаешься с «красивым» материалом. К ним можно отнести тему "Правильные многоугольники" (на доске написана тема урока «Построение правильных многоугольников»)

Название «правильных» идет из античных времен. Древнегреческие ученые проявляли большой интерес к правильным фигурам еще со времен Пифагора. В египетских и вавилонских старинных памятниках встречаются правильные четырехугольники, шестиугольники, восьмиугольники в виде изображений на стенах и украшений, высеченных из камня. Правильные многоугольники привлекали к себе внимание ученых, строителей, архитекторов и многих других. Нас поражает красота, гармония многогранников, образованных простейшими правильными многоугольниками одного типа (слайд 10)

Вот для рабочего кабинета настольный календарь 2010 года, имеющий форму додекаэдра. Обратим внимание на то, что гранями многогранников являются правильные многоугольники: правильные треугольники, правильные четырехугольники, а правильные шестиугольники не могут являться гранями многогранников. Это связано с тем, что сумма плоских углов при вершине многогранников меньше 360 градусов.

Знания о правильных многоугольниках применяются в разных профессиях. Например, ювелир вставляет дорогой камень в золотую оправу. Слесарь подбирает ключ для болтика формы правильного многоугольника и т.д. Решенные нами задачи также нас показывают, что без знаний о правильных многоугольниках нам не обойтись. Они встречаются в жизни везде (слайд 11).

Итак, тема «Построение правильных многоугольников», как мы видим, актуальна.

Запишем тему урока «Построение правильных многоугольников» (слайд 12).


4. Изучение нового материала

В математике есть специальные задачи на построение, которые решаются только с помощью циркуля и линейки. Что же можно делать с помощью линейки и что с помощью циркуля?

• Ясно, что линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки.
  
• С помощью циркуля можно провести окружность произвольного радиуса, а также с центром в данной точке и радиусом, равным данному отрезку; можно отложить отрезок заданной длины (слайд 13).
  

Выполняя эти несложные операции, мы можем решать разные задачи на построение.

В 7 классе мы с вами изучали ряд простейших построений циркулем и линейкой:

• биссектрисы угла;
  

• через данную точку провести прямую, перпендикулярную к данной прямой;
  
• разделить данный отрезок пополам;
  
• построение угла, равного данному.;
  
• построение треугольников по трем заданным элементам и т.д.
  

Домашним заданием было повторение решений этих задач.

а) через точку на прямой

б) через точку, не лежащую на прямой

в)построение перпендикулярной прямой.


Ученики комментируют решение по слайду 14 - деление отрезка пополам.


Оценить работу ученика, выполнившего построение перпендикулярной прямой через точку, не лежащую на данной прямой (слайд 15).


Интереснейшей задачей на построение с помощью циркуля и линейки является практическая задача построения правильного многоугольника с заданным числом сторон, поставленная еще в глубокой древности. Решение этой задачи можно найти в трудах древнегреческих ученых Архимеда, Евклида, Пифагора, математика 17-18 веков Гаусса (слайд 16).

Еще в 5-6 веке до нашей эры Евклидом были решены задачи на построение правильного треугольника, четырехугольника, шестиугольника, пятнадцатиугольника с помощью циркуля и линейки (слайд 17).

Сегодня мы с вами рассмотрим способы построения некоторых правильных многоугольников.

Цель урока: научиться строить правильные треугольники, четырехугольники, пятиугольники, шестиугольники и некоторые другие правильные многоугольники:

• с помощью циркуля и линейки;
  
• также с помощью компьютера
  

.


Построения правильных треугольника, квадрата, шестиугольника несложны. Вспомним построение треугольника по трем равным сторонам (слайд 18, ссылка на презентацию «Построение правильного треугольника»).

Проведем прямую и на ней отложим отрезок АВ. Затем построим две окружности: с центром в точке А и центром в точке В радиуса АВ.



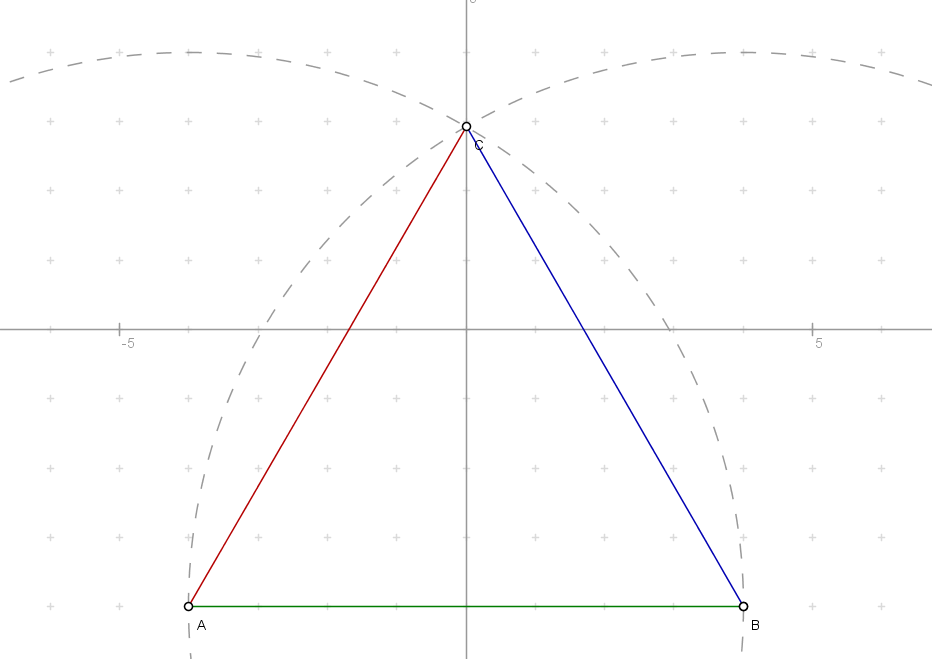
Построение квадрата.

• Так как диагонали квадрата взаимно-перпендикулярны и в точке пересечения делятся пополам, то можно построить так: Оценить ответ 2 ученика.
  

Мы при построении квадрата воспользовались его свойствами.

• Предложить учащимся еще 1 способ построения правильного четырехугольника.
  

Если вспомнить определение квадрата, то можно применить следующий способ.

(Электронный учебник «Геометрия в 9 классе» (Кирилла и Мефодия)- кадр «Построение правильного четырехугольника»).

Для построения правильных многоугольников обычно используется окружность, описанная около многоугольника. Чтобы построить правильный n-угольник, достаточно разделить окружность на n равных дуг, тогда точки деления будут его вершинами (кадр «Построение правильного многоугольника»).

Центральные углы равны 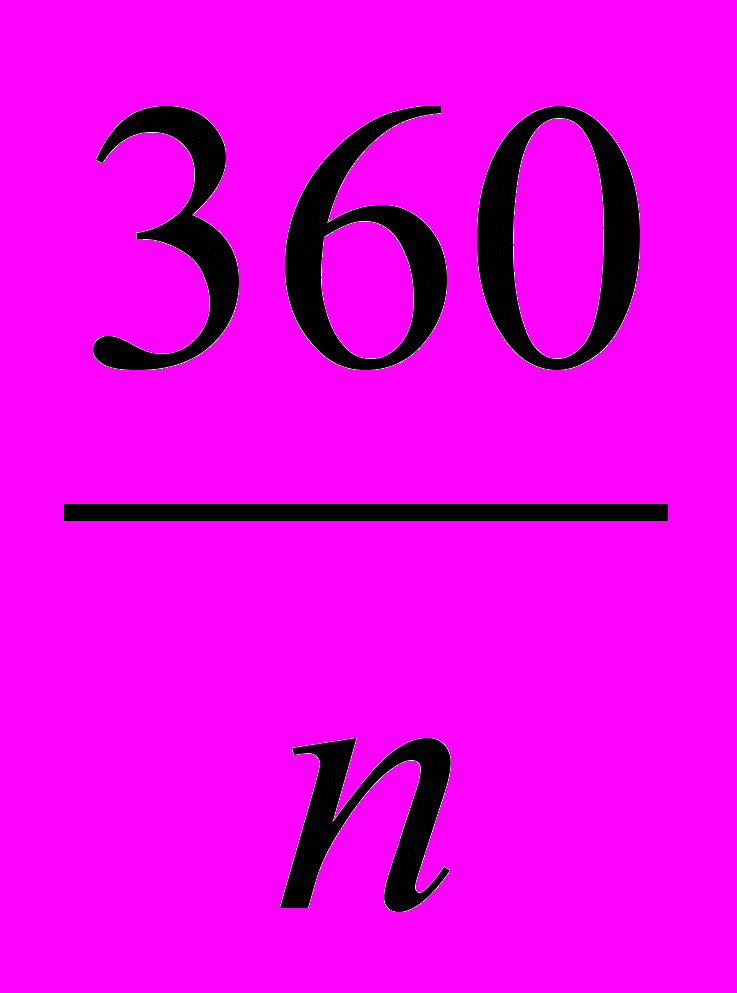градусов.

Треугольники равны по 2 сторонам и углу между ними. Следовательно, отрезки А₁А₂ =А₂А₃=….,

если все стороны вписанного многоугольника равны, то он является правильным. Итак, при любых натуральных значениях n≥3 существует правильный n-угольник. В некоторых случаях задача о построении правильных n-угольников решается с помощью циркуля и линейки.

Задача 1.

7 кадр «Построение правильного четырехугольника, вписанного в окружность» (ребята выполняют в тетради).

Задача 2. Построить правильный шестиугольник (слайд 210.

8 кадр. Построение правильного шестиугольника, вписанного в окружность

Ребята выполняют построение в тетради.

Ребята, можно ли построить правильный треугольник с помощью окружности? Да (слайд 22).

Задача 3.Построить правильный пятиугольник (ребята выполняют в тетради, 2 ряд выполняет на цветной бумаге)

Опорная схема на столах

Построение правильного пятиугольника выполните дома, пользуясь опорной схемой.

Посмотрите, как нужно работать.

Пользуясь опорной схемой, дети строят в своих тетрадях правильный пятиугольник (слайды 23, 24).

Для построения правильных многоугольников часто используется следующая задача:

Дан правильный n-угольник. Построить правильный 2n угольник.

Мы уже говорили, что построение n-угольника эквивалентно делению окружности на n равных дуг. Дугу легко разделить пополам, построив биссектрису соответствующего центрального угла. (Электронный учебник «Геометрия в 9 классе» Кирилла и Мефодия - кадр «Построение правильного 2n- угольника»).

Практическая работа на примере восьмиугольника (дети строят в тетради), 25 слайд.

Применяя указанный способ можно с помощью циркуля или линейки построить целый ряд правильных многоугольников, если построен один из них.

Например. Построив правильный четырехугольник, можно построить правильный восьмиугольник, правильный шестнадцатиугольник и вообще правильный 2^k угольник, где k>2.

Долгое время математики тщетно искали способы построения правильного семиугольника, девятиугольника, не зная даже вообще возможны ли эти построения.

В решении поставленной проблемы построения правильных многоугольников большой вклад внес немецкий математик Гаусс (1801 г). Он открыл способ построения правильного 17-угольника только с помощью циркуля и линейки и указал все значения n, при которых возможно построение правильного n-угольника указанными средствами. Этими многоугольниками оказались лишь многоугольники, у которых количество сторон является простым числом вида (2 в степени 2^k )+1 или а также те, которые получаются из них удвоением числа сторон.

Таким образом, с помощью циркуля и линейки оказалось невозможным построение правильного 7, 9,11, 13, 14, 18, 19, 21, 22, 23, 25, 27, 28….- угольников и т.д.

(Материал взят из электронного учебника «Геометрия в 9 классе» Кирилла и Мефодия) .

3,4,5,6,8,10,12,15,16,17,20,24,30,32,34,40 … - угольники можно построить. Гаусс описал даже построение правильного 257-угольника только с помощью циркуля и линейки.

7, 9,11, 13, 14, 18, 19, 21, 22, 23, 25, 27, 28… – угольники невозможно построить только с помощью циркуля и линейки (слайд 26).

Однако в практических построениях нас никто не ограничивает в выборе математических инструментов. Сейчас вы будете строить правильные многоугольники методом моделирования при отсутствии специальных инструментов, имея компьютер (учитель информатики).

Физкультминутка (слайд 28).

Учитель информатики.

На уроке информатики мы с вами изучали тему «Модель и моделирование». Вспомним основные определения (слайд 29).

• Модель – это упрощённое подобие предмета или процесса. Она повторяет какие-то свойства оригинала и заменяет его в некоторых случаях.
  
• Модель — способ замещения реального объекта, используемый для его изучения.
  

Моделирование – процесс создания модели предмета.

На прошлых уроках мы моделировали объекты в текстовом редакторе, в электронной таблице и в графическом редакторе. Сегодня мы с вами посмотрим, как можно моделировать не объект, а процесс, т.е моделировать функции линейки, циркуля, транспортира по готовым алгоритмам. Построим правильные многоугольники в графической среде.

Учащиеся первого ряда садятся за свои компьютеры (построить правильные четырехугольники и правильные шестиугольники, алгоритмы на листочках лежат около компьютеров). По завершении работы сохраните как «многоугольник» в папке «Мои рисунки» (слайды 30, 31).

В это время 1 ученик за основным компьютером выполняет построение правильного треугольника с объяснением, остальные смотрят на экран.

Учитель информатики. Итак, мы убедились, что моделировать процесс построения правильных многоугольников с помощью графического редактора можно. Нужно лишь сначала написать или продумать план действий.

А как можно нарисовать правильные многоугольники очень быстро? Конечно, с помощью компьютерных программ. Существует множество готовых программ по конструированию, проектированию, моделированию объектов.



Сегодня я хочу вас познакомить одной из таких программ, которая называется «StarCad». (Демонстрация программы: построение пятиугольника с комментарием) (слайд 32).



Учитель математики.

Правильные многоугольники встречаются в природе. Одним из примеров являются

пчелиные соты, которые представля­ют собой прямоугольник, покрытый (т.е. составленный, обращаем внимание, без просветов и перекрытий) правильными шестиугольника­ми.

Ребята, пчелы - удивительные творцы, вы об этом все знаете. Обратите внимание, соты пчел имеют форму правильного шестиугольника. Плоскость прямоугольника покрыта этими правильными шестиугольниками без просветов и наложений (слайды 33, 34).

Сейчас мы с вами попробуем покрыть плоскость построенными вами правильными многоугольниками без просветов и перекрытий.

Учитель информатики.

Алгоритм покрытия плоскости без просветов и перекрытий:

1. Выделяем выбранный многоугольник.

2. Одновременно с нажатием кнопки Ctrl передвигаем многоугольник с помощью мышки, вставляя так, чтобы исходный многоугольник и его копия соприкасались сторонами (слайд 35).

За компьютеры - садится 1 ряд (покрытие плоскости без просветов и наложений правильными четырехугольниками и правильными шестиугольниками, за основной -1 ученик, работает с объяснением, выполняет покрытие плоскости правильными треугольниками.

Учитель математики.

Параллельно проводится лабораторная работа – покрытие плоскости без просветов и наложений правильными пятиугольниками.

Работа в группе из 6 человек.

Задание: вырезать напечатанные правильные пятиугольники и покрыть ими плоскость без просветов и наложений т.е. перекрытий.

3 ученика решают по карточке у доски.

а) вычислить периметр и площадь правильного треугольника со стороной 4 см;

б) вычислить периметр и площадь правильного четырехугольника со стороной 3 см;

в) вычислить периметр и площадь правильного четырехугольника со стороной 2 см.

Выступление ученика - защита исследовательской работы «Геометрические паркеты из правильных многоугольников». Делается вывод, что плоскость можно покрыть без просветов и перекрытий только правильными треугольниками, четырехугольниками, правильными шестиугольниками.

Ребята, а вы никогда не задумывались над тем, почему пчелы строят свои соты в форме правильных шестиугольников? (слайд 37).

Ответ на этот вопрос нам даст решение этих задач (проверить работу учеников, работавших у доски):

а) вычислить периметр и площадь правильного треугольника со стороной 4 см.

Ответ. S=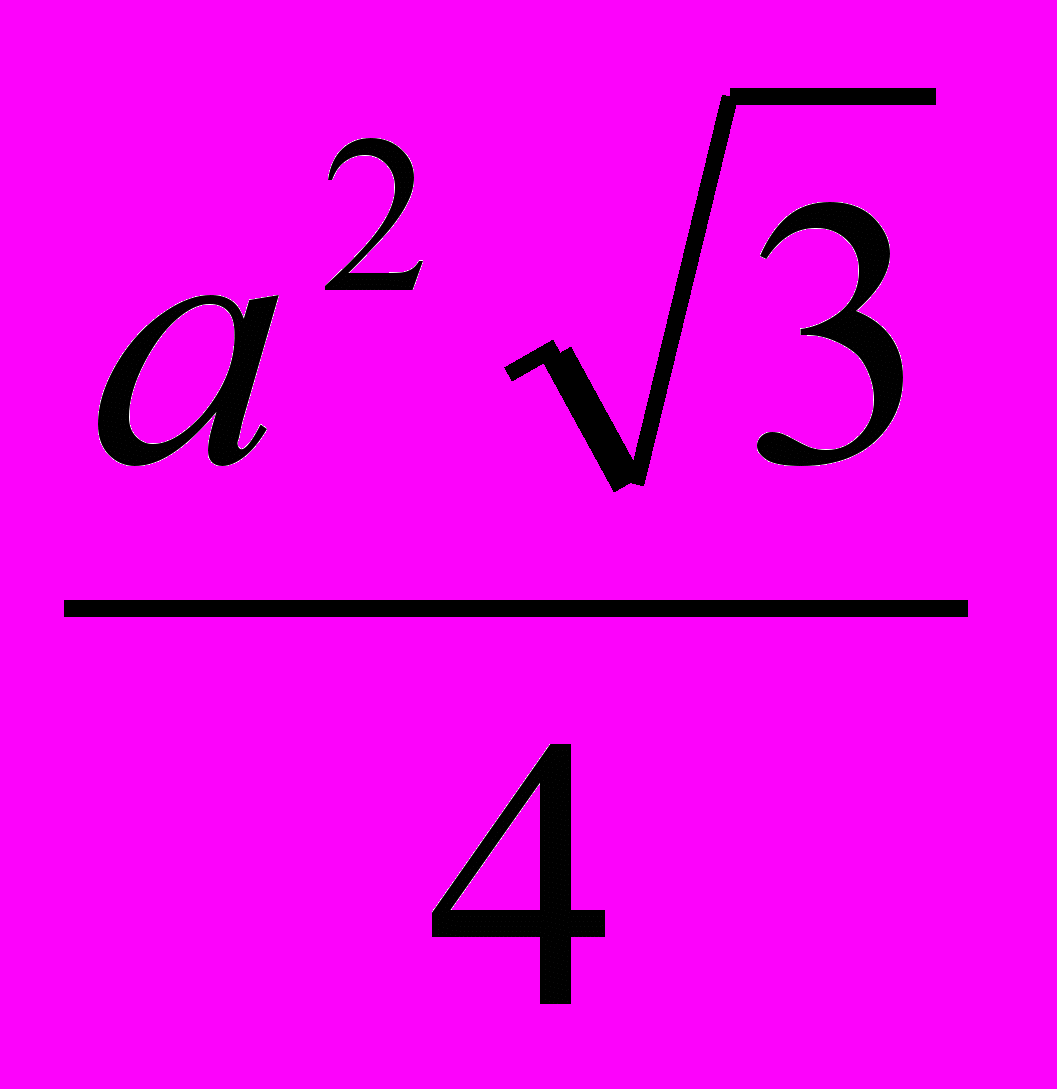=4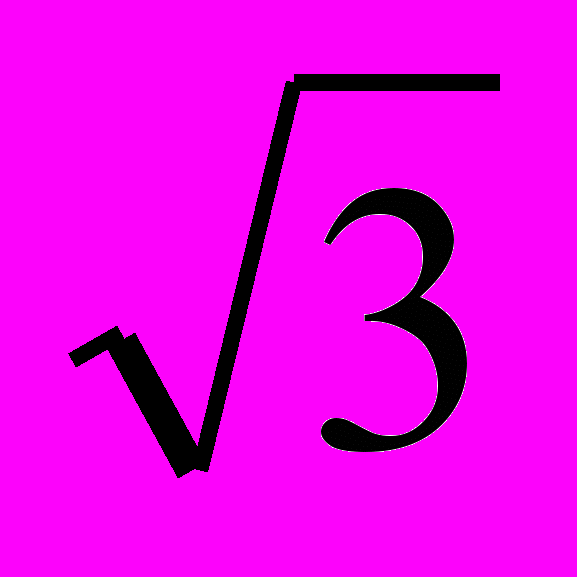; Р=12 см.

б) вычислить периметр и площадь правильного четырехугольника со стороной 3 см.

Ответ. Р=12 см.

S=9 кв.см

в) вычислить периметр и площадь правильного четырехугольника со стороной 2 см.

Ответ.Р=12 см.

S=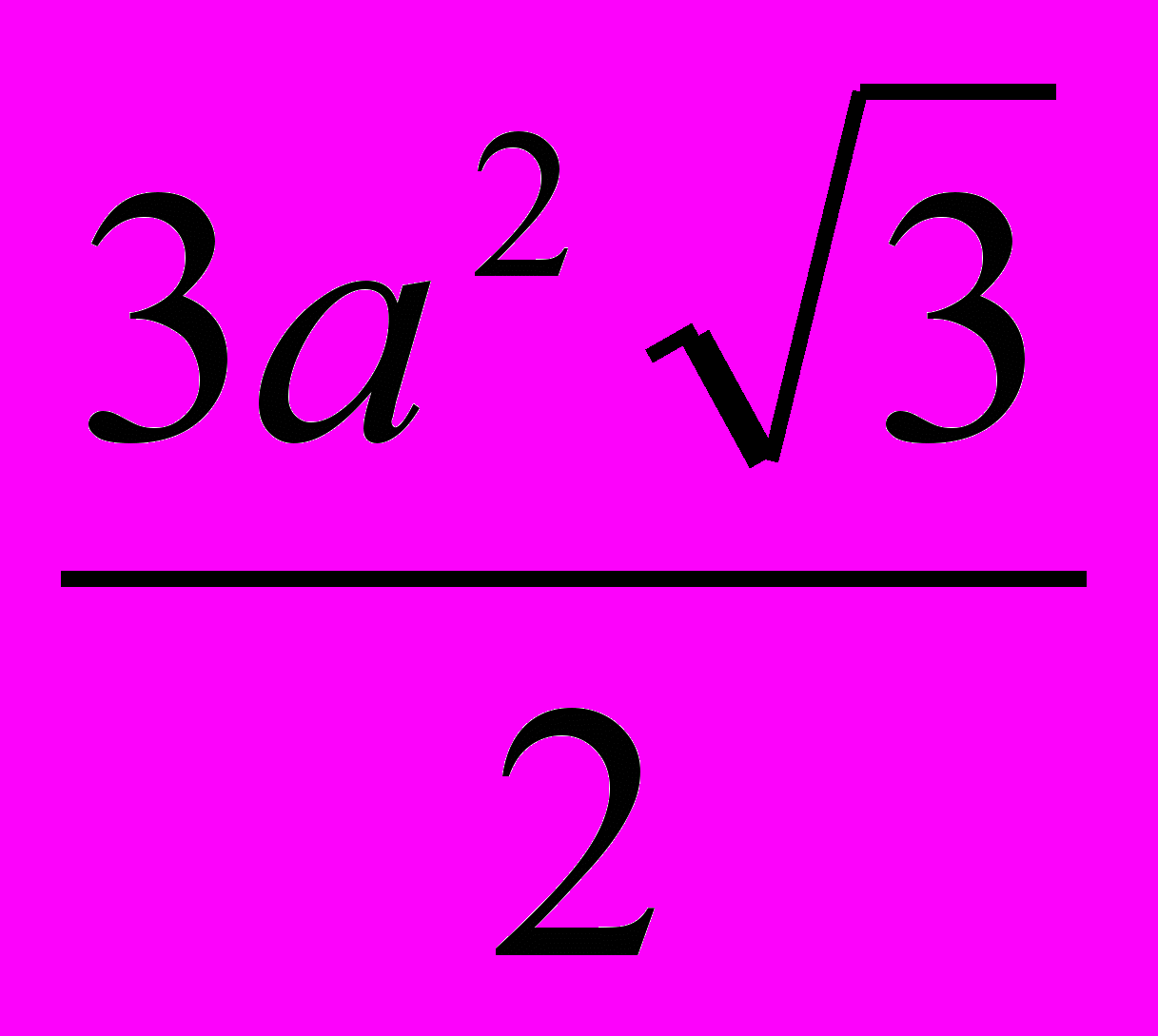=6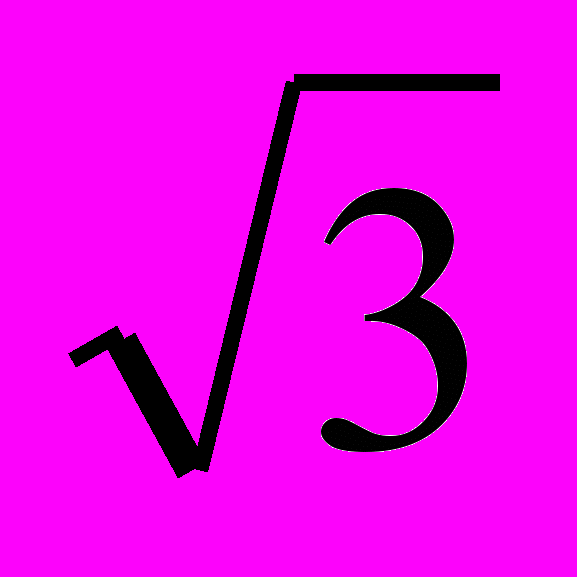

Вывод. При заданном периметре площадь больше в третьем случае. Во всех случаях воска уходит одинаковое количество, а вместимость больше.

Следовательно, при построении сотых в форме правильных шестиугольников экономится воск.

5.Итоговое тестирование на компьютере (слайд 38).

На компьютере выполняют тесты 9 учеников, выполняется работа в 2 варианта.

1 вариант.

1.Выберите верные утверждения

1.Если все углы многоугольника равны, то он является правильным.

2.Если все стороны многоугольника равны, то он является правильным.

3. Любой выпуклый многоугольник является правильным.

4.Любой правильный многоугольник является выпуклым.

2. Какой правильный многоугольник всегда можно построить с помощью циркуля и линейки, если дан правильный n-угольник?

1. Правильный (n-1) угольник

2. Правильный 2n- угольник

3. Правильный 3n- угольник

4. Правильный (n+1) угольник

3.Какие из перечисленных правильных многоугольников нельзя построить с помощью циркуля и линейки?

1. Правильный семиугольник.

2. Правильный восьмиугольник

3. Правильный шестиугольник

4. Правильный пятиугольник

4.Какие утверждения неверны?

1. Сторона правильного шестиугольника, вписанного в окружность, равна радиусу этой окружности.

2. Треугольник является правильным, если все его углы равны.

3. Любой равносторонний треугольник является правильным.

4.Любой четырехугольник с равными сторонами является правильным.

5. Найти площадь правильного четырехугольника, если радиус окружности, описанной около этого четырехугольника, равна 3

Ответы:

1. 2

2. 4

3. 18

4. 27

2 вариант.

1. Какой правильный многоугольник всегда можно построить с помощью циркуля и линейки, если дан правильный n-угольник?

1. Правильный (n-1) угольник

2. Правильный 2n- угольник

3. Правильный 3n- угольник

4. Правильный (n+1) угольник

2.Выберите верные утверждения

1.Если все углы многоугольника равны, то он является правильным.

2.Если все стороны многоугольника равны, то он является правильным.

3. Любой выпуклый многоугольник является правильным.

4.Любой правильный многоугольник является выпуклым.

3.Какие утверждения неверны?

1. Сторона правильного шестиугольника, вписанного в окружность, равна радиусу этой окружности.

2. Треугольник является правильным, если все его углы равны.

3. Любой равносторонний треугольник является правильным.

4.Любой четырехугольник с равными сторонами является правильным.

4.Какие из перечисленных правильных многоугольников нельзя построить с помощью циркуля и линейки?

1. Правильный семиугольник.

2. Правильный восьмиугольник

3. Правильный шестиугольник

4. Правильный пятиугольник

5. Найти площадь правильного четырехугольника, если радиус окружности, описанной около этого четырехугольника, равна 2

Ответы:

1. 2

2. 4

3. 8

4. 12

Проводится блеф-клуб с остальными учениками, раздать листочки.

Верите ли вы, что: Отвечать только да или нет.

1. Около любого правильного многоугольника можно описать окружность и притом только одну.
   
2. В любой многоугольник можно вписать окружность.
   
3. Если стороны вписанного многоугольника равны, то он является правильным.
   
4. Любой четырехугольник с равными сторонами является правильным.
   
5. С помощью циркуля и линейки можно построить правильный двенадцатиугольник.
   
6. Сумма внешних углов правильного треугольника равна .
   
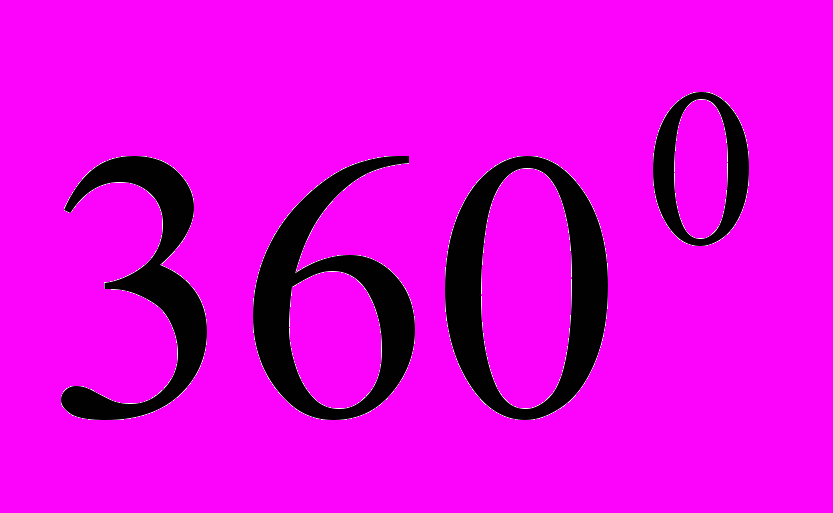7. Ромб – правильный четырехугольник.
   
8. По данному n-угольнику можно ли построить правильный 2 n – угольник.
   
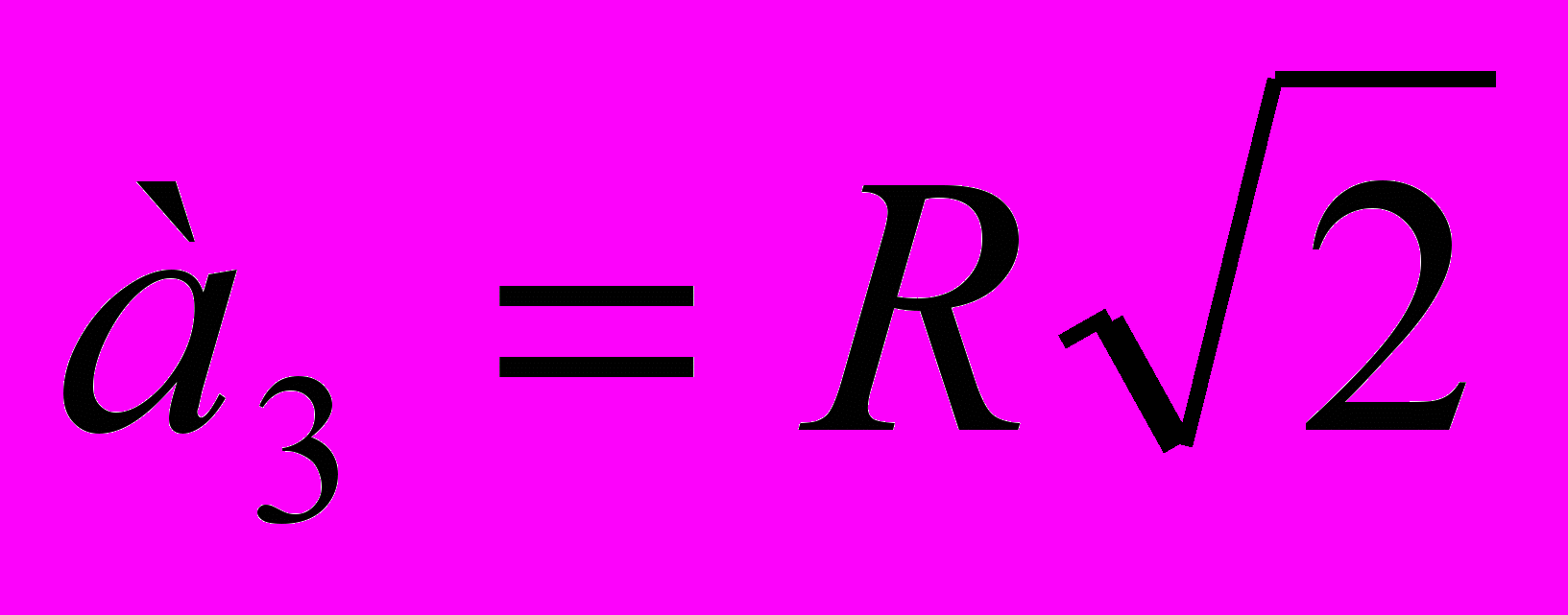9. - сторона правильного треугольника.
   
10. Площадь правильного многоугольника можно вычислить по формул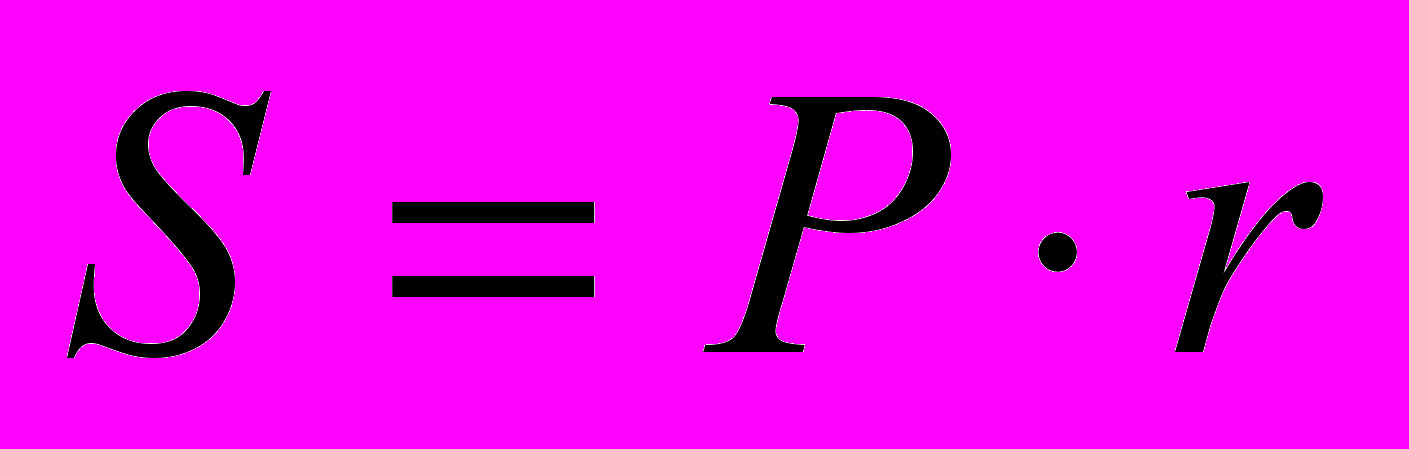е , где 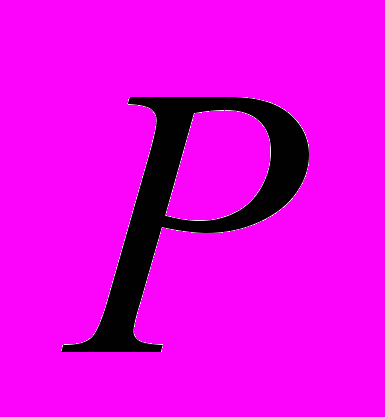- периметр многоугольника, а 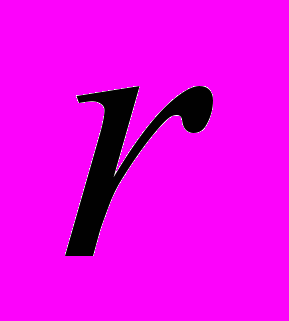- радиус вписанной окружности.
    

Ответы.

Да – 1, 3, 5, 6, 8.

Нет -2, 4, 7, 9, 10.

Самооценка.

10 заданий- «5»

8 заданий - «4»

6 зданий - «3»

1-5 заданий – «2» .


6. Итог урока. Обобщение всех полученных результатов, оценить работы учащихся за урок. Использование учителем позитивных оценок (вербальных и невербальных) в виде похвалы, одобрения.


Задание на дом: п. 109, упр. 1090 с объяснением (слайд 39), 1098.

Слайд 40.