Многопериодных стохастических моделей

Вид материала

Автореферат диссертации

Содержание Краткое введение Общая характеристика работы Цель и задачи исследования Объектом исследования Положения, выносимые на защиту Личный вклад соискателя Апробация результатов диссертации Опубликованность результатов диссертации Структура и объем диссертации Основное содержание Метод исторического моделирования Метод параметрической оценки (вариационно-ковариаци­онная модель) Метод имитационного моделирования Монте-Карло Рисунок 1 – Алгоритм практической реализации инструментальногометода управления портфелем ценных бумаг Рисунок 2 – Результаты применения статической и динамической стратегии управления портфелем на прошлых данных с различными длина Основные научные результаты диссертации Рекомендации по практическому использованию результатов Список публикаций соискателя по теме Мэта работы Метады даследавання ... Полное содержание

Подобный материал:

• Анализируются свойства медианных скользящих фильтров при их использовании для обработки, 68kb.
• 1. Классификация моделей представления знаний, 1008.73kb.
• «Разработка моделей и образцов стандартов для бакалавров и магистров по специальности», 3866.49kb.
• 1. Введение Основы анализа данных. Методология построения моделей сложных систем. Модель, 399.94kb.
• Лекции по дисциплине «Математическое моделирование» для студентов и магистрантов специальности, 21.92kb.
• Самостоятельная работа 2 часа в неделю всего часов, 42.13kb.
• Положение о городском конкурсе моделей ученического самоуправления общеобразовательных, 101.39kb.
• Урок №1 Тема: «Понятие модели. Назначение и свойства моделей. Виды моделей», 139.14kb.
• Исследование математических моделей, 9.9kb.
• Устойчивое развитие: экоэтический потенциал моделей, 254.76kb.

АКАДЕМИЯ УПРАВЛЕНИЯ ПРИ ПРЕЗИДЕНТЕ

РЕСПУБЛИКИ БЕЛАРУСЬ


УДК 336:330.4(043.3)


КАРАЧУН

ИРИНА АНДРЕЕВНА


ОПТИМИЗАЦИЯ ПОРТФЕЛЯ ЦЕННЫХ БУМАГ НА ОСНОВЕ

МНОГОПЕРИОДНЫХ СТОХАСТИЧЕСКИХ МОДЕЛЕЙ


Автореферат диссертации на соискание ученой степени
кандидата экономических наук

по специальности 08.00.13 – математические и инструментальные методы
экономики


Минск, 2011

Работа выполнена в  Белорусском государственном университете

Научный руководитель:	Ковалев Михаил Михайлович, доктор физико-математических наук, профессор, декан экономического факультета Белорусского государственного университета
Официальные оппоненты:	Самаль Сергей Александрович, доктор экономических наук, доцент, ректор ЧУО «БИП – Институт правоведения» Синявская Ольга Александровна, кандидат экономических наук, доцент, доцент кафедры экономической информатики факультета менеджмента УО «Белорусский государственный экономический университет»
Оппонирующая организация:	УО «Белорусский государственный университет информатики и радиоэлектроники»

Защита состоится 14 сентября 2011 г. в 15.00 часов на заседании совета по защите диссертаций Д 07.01.01 при Академии управления при Президенте Республики Беларусь по адресу: 220007, г. Минск, ул. Московская, 17, ауд. 203,
E-mail: post@pac.by, тел.: 222-76-42.


С диссертацией можно ознакомиться в библиотеке Академии управления при Президенте Республики Беларусь.


Автореферат разослан 13 июня 2011 года.

Ученый секретарь совета по защите диссертаций

Зеневич А.М.

КРАТКОЕ ВВЕДЕНИЕ


Программа развития рынка ценных бумаг Республики Беларусь предусматривает: снятие ограничений на эмиссию и обращение ценных бумаг, в особенности акций; снижение государственного участия на рынке ценных бумаг; упрощение процессов обращения ценных бумаг; снижение ставок налогов на доходы от операций с ценными бумагами; придание национальным ценным бумагам привлекательности для зарубежных инвесторов; интеграцию национального рынка ценных бумаг в мировую экономику. Наряду с задачей развития рынка ценных бумаг, сформулированной в направлениях социально-экономического развития Республики Беларусь, рост числа акционерных обществ (в проект плана приватизации на 2011–2013 гг. внесено около 300 объектов) неизбежно приведет к активизации деятельности, направленной на осуществление различных операций с финансовыми активами. Учитывая специфику подобной деятельности, лицам, принимающим управленческие решения, необходим надежный инструментарий для проведения эффективной стратегии в финансовой среде. Недостаточное развитие инструментов исследования рынка капитала и ценных бумаг отрицательно сказывается на уровне экономической активности белорусских предприятий. Вместе с тем использование финансовых инструментов в практической деятельности коммерческих организаций может повысить эффективность инвестиционной деятельности, оптимизировать структуру капитала и качественно улучшить управление оборотными средствами и финансовыми активами.

В настоящее время существует теоретическая основа для разработки инструментов по системному управлению финансовыми активами корпоративных структур. Но прикладные приложения в виде классических моделей финансовой математики, основанных на статистических методах, в основном ориентированы на специфику стран с устоявшейся рыночной экономикой
и традициями использования фондовых активов в качестве способа сбережения накопленных средств, а также получения дохода без значительных затрат производственных ресурсов. В условиях же малых экономик, в которых
существование рыночных отношений не имеет столь длительной истории, подобные приложения могут быть использованы либо с существенными ограничениями, либо могут быть неприменимы вовсе. В соответствии с этим возникает проблема разработки таких экономико-математических инструментов, которые бы учитывали не только эти особенности рынка ценных бумаг стран с переходной экономикой, но и могли бы быть совместимыми с уже имеющимися на мировом финансовом рынке моделями оценки финансовых активов.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ


Связь работы с крупными научными программами
(проектами) и темами

Результаты, изложенные в диссертации, получены в рамках исследований, проводимых на кафедре банковской и финансовой экономики Белорусского государственного университета в соответствии со следующими научно-исследовательскими работами: «Воздействие финансовой и денежно-кредитной политики на инновационное развитие национальной экономики» (№ 20081259 от 1.01.2008) раздел темы «Методика оптимального управления структурой портфельных инвестиций коммерческого банка», «Разработка стратегии развития ОАО «МКСИ» на 5 лет» (№ 98833 от 28.12.2009), «Разработка механизма эффективного контроля банками платежеспособности предприятий АПК при осуществлении экспортно-импортных операций» (№ 98835 от 10.01.2010).

Тема диссертации соответствует следующим приоритетным направлениям фундаментальных и прикладных научных исследований, утвержденным Постановлением Совета Министров Республики Беларусь от 17.05.2005 № 512 «Об утверждении перечня приоритетных направлений фундаментальных и прикладных научных исследований Республики Беларусь на 2006–2010 годы»: 6.1. Математические модели и их применение к анализу систем и процессов в природе и обществе, 9.2. Механизмы устойчивого инновационного развития Беларуси во взаимодействии с мировым научным и научно-технологическим пространством. Диссертационная работа выполнялась с учетом основных положений Национальной стратегии устойчивого социально-экономического развития Республики Беларусь на период до 2020 г., Программы развития рынка корпоративных ценных бумаг 2008–2010 гг.

Цель и задачи исследования

Целью исследования является разработка и применение методов, моделей и методик управления портфелем ценных бумаг инвестора с позиций максимизации дохода и ограничения размера потерь в условиях стохастической неопределенности динамики рыночной ситуации.

Для её достижения поставлены и решены следующие задачи:

• выявить, на основании сравнительного анализа методов и методик выбора оптимальной структуры финансовых инвестиций в ценные бумаги, используемых в мировой практике, наиболее перспективные для использования в инвестиционной деятельности коммерческих организаций Республики Беларусь;
  
• разработать комплекс многопериодных стохастических моделей оптимизации портфеля ценных бумаг, позволяющих дифференцировать методы измерения и ограничения риска в зависимости от длины горизонта инвестирования;
  
• осуществить разработку методики оптимизации портфеля с производными ценными бумагами, сочетающую в себе дифференцированный подход к измерению риска с возможностью учета особенностей ценообразования каждого портфельного актива;
  
• разработать инструментальный метод управления портфелем ценных
  бумаг с учетом динамических изменений рыночной ситуации, позволяющий инвестору оперативно обрабатывать рыночную информацию, формировать портфель и принимать решения по выполнению необходимых операций в течение горизонта инвестирования.
  

Объектом исследования выступает процесс осуществления портфельных финансовых инвестиций в ценные бумаги. Предмет исследования – методы, модели и методики оптимизации и управления портфелем ценных бумаг различного видового состава в условиях динамично изменяющейся рыночной ситуации. Выбор объекта и предмета обусловлен недостаточностью математического обоснования и инструментальных методов оценки рыночного риска применительно к специфике ценных бумаг различного качества и современной направленности рынка ценных бумаг.

Положения, выносимые на защиту

1. Комплекс многопериодных стохастических моделей оптимизации портфеля первичных ценных бумаг, обеспечивающих учет величины допустимых потерь капитала инвестора. В основе моделей заложены адаптированные к получению базового уравнения динамики портфеля уравнения модели Блека-Шоулза, что обеспечивает реализацию алгоритма расчета математического ожидания функции дохода портфеля как целевой функции в решении оптимизационной задачи. Новизна моделей состоит в возможности определения с их помощью меры риска для ценных бумаг с различным горизонтом инвестирования на основе двух вариаций меры риска (Conditional Value-at-Risk и Conditional Capital-at-Risk). Результат решения позволяет дифференцировать измерение рисков по краткосрочному и среднесрочному периоду инвестирования, требуемое для оптимизации портфеля инвестора с учетом динамической компоненты.

2. Методика оптимизации смешанного портфеля первичных и производных ценных бумаг. Задача оптимизации смешанного портфеля сведена к устранению проблемы описания нелинейной портфельной динамики, затрудняющей моделирование и прямой расчет меры риска при распределении инвестированного капитала. Новизна предложенной методики состоит в том, что она отражает процесс нахождения долей портфельных активов путем математического анализа модифицированного уравнения динамики смешанного портфеля, полученного через механизм реплицирования портфельных опционов первичными активами. Проведенная апробация корректности работы методики применительно к портфелю с колл-опционами показала, что достигается синхронизация распределения долей смешанного портфеля и долей портфеля первичных ценных бумаг с корректировкой на дельту опциона. Использование предложенной методики в практической деятельности профессиональных участников рынка ценных бумаг (банков, небанковских финансовых организаций) позволит органам банковского надзора повысить качество пруденциального регулирования банковской системы, а также улучшить риск-менеджмент финансовых организаций Республики Беларусь.

3. Инструментальный метод управления портфелем ценных бумаг в условиях динамических изменений рыночной ситуации, включающий вариативный подход к выбору оптимизационной модели в зависимости от вида активов и длины инвестиционного горизонта (краткосрочный, среднесрочный), а также процедуры составления таблиц распределения капитала инвестора с учетом его склонности к риску и складывающейся рыночной ситуации. Активизация динамической (рыночной) компоненты осуществляется при условии, что нарушились пропорции в сегментах внешней среды. Анализ динамических изменений структуры портфеля обеспечивает инвестора необходимыми информационными ресурсами для принятия решения по купле-продаже ценных бумаг с целью воссоздания оптимальной структуры. Отличительной особенностью данного метода от существующих является структурно-логическая схема выбора оптимизационной модели, позволяющая снять ограничения на состав и срок владения портфелем, что обеспечивает инвестору инструмент повышения уровня контроля над структурой портфельных активов относительно изменения рыночной ситуации на любом временном отрезке. Перспективность предложенной схемы в том, что она имеет широкую область приложения, в частности, может использоваться физическими лицами для управления мультивалютными счетами, а также портфелями финансовых инструментов на рынке Forex.

Личный вклад соискателя

Все результаты диссертационного исследования, в том числе положения, выносимые на защиту, получены соискателем самостоятельно. В совместно опубликованных по теме диссертации работах соискателю принадлежат положения, изложенные в диссертации, остальным соавторам – общие вопросы теории оптимизации и стохастического анализа.

Апробация результатов диссертации

Основные результаты диссертационного исследования докладывались и получили положительную оценку на следующих научно-практических конференциях: «Математическая физика, математическое моделирование и компьютерная математика» (Гродно, 2004), «Управление в социальных и экономических системах» (Минск, 2005), «ECCO XVIII – Combinatorics for modern manufacturing, logistics and supply chains» (Minsk, 2005), «Интеллектуальные технологии в образовании, экономике и управлении» (Воронеж, 2005, 2007), «Аналитические методы анализа и дифференциальных уравнений (AMADE-2006)» (Минск, 2006), «Еругинские чтения-XI» (Гомель, 2006), «Актуальные проблемы развития финансово-кредитного механизма в инновационной экономике» (Минск, 2007), «Актуальные проблемы экономики и совершенствования правового регулирования в экономике» (Пятигорск, 2009), «Экономика и управление: теория и практика» (Самара, 2009), «Национальная экономика в условиях глобального кризиса: пути инновационного развития» (Минск, 2009), «Гибридный интеллект» (Воронеж, 2009), «Новые свойства посткризисной экономики. Место Беларуси в посткризисном мире» (Минск, 2009), «Теоретико-методологические и прикладные аспекты государственного управления» (Минск, 2010).

Опубликованность результатов диссертации

По теме диссертации опубликовано 27 научных работ, в том числе: 3 статьи в научных журналах, соответствующих п. 18 Положения о присуждении ученых степеней и присуждении ученых званий в Республике Беларусь (1,6 авторских листа), 4 – в иных изданиях, 20 материалов конференций и тезисов докладов. Общий объем публикаций составляет 7,3 авторских листа.

Структура и объем диссертации

Диссертация состоит из перечня условных обозначений, введения, общей характеристики работы, трех глав, заключения, библиографического списка, включающего 154 наименования (в том числе 27 публикаций соискателя), и приложений. Работа изложена на 157 страницах. Объем, занимаемый 6 таблицами, 19 рисунками, библиографическим списком и 12 приложениями, составляет 68 страниц.

ОСНОВНОЕ СОДЕРЖАНИЕ


В главе 1 «Теоретико-методологические подходы к оптимизации портфеля ценных бумаг» представлены результаты исследования методологических подходов к решению задач оптимального размещения средств в ценные бумаги с учетом ограничений уровня риска и тенденций развития рынка
ценных бумаг.

Исследованием установлено, что в эволюции научных взглядов на проблему управления портфельными инвестициями выделяется несколько направлений: объяснение поведения финансовых активов и на его основе создание моделей оценки их будущей доходности и объединения в портфель; методическая разработка проблемы оптимизации портфеля ценных бумаг в различных условиях функционирования рынка; формирование математической поддержки решения задач по управлению портфелем ценных бумаг и алгоритмов их реализации. Изучение специфики отмеченных направлений позволило сделать вывод о недостаточной изученности проблемы поведения портфельных инвестиций в условиях неопределенности и быстрого усложнения рыночной среды (появление новых альтернативных активов, в том числе производных ценных бумаг; глобализация финансовых потоков; появление новых информационных систем торговли финансовыми активами).

Анализ существующих методик измерения риска позволил выделить три направления их использования: измерение чувствительности цены актива к изменению внешних условий; оценка дисперсии и среднеквадратического отклонения; оценка вероятности возможного убытка. Выбор направления использования методики конкретным инвестором зависит от его стратегических предпочтений по вложению средств и от уровня структурированности рыночной среды. При этом важен критерий ранжирования риска инвестором. Проведенный обзор литературы показал, что в подавляющем большинстве при слабо структурированном целевом рынке таким критерием является надежность инвестиций. Однако, учитывая специфику среды инвестиционной деятельности, методики, реализующие какое-либо одно из направлений, не отвечают требованию надежности оценок в оптимизационной модели.

Исследование инструментальных подходов к оценке риска портфеля показало, что самые популярные на сегодняшний день меры риска основываются на методологии Value-at-Risk (VaR), разработанной группой RiskMetrics (базовые методы расчета представлены в таблице 1). В соответствии с Basel II Банк международных расчетов определил её стандартной для банков. Это связано с тем, что капитал банка должен соответствовать его рискам, которые необходимо уметь определять, чтобы формулировать требования к капиталу, обеспечивающие банку надежность. В связи с этим назрела необходимость в разработке практических инструментов, позволяющих адекватно оценивать риски портфельных инвестиций на основе указанной методологии и построении моделей оптимизации портфелей ценных бумаг в соответствии с нормативными требованиями.


Таблица 1 – Классические подходы к оценке VaR портфеля ценных бумаг

Принцип расчета	Достоинства	Недостатки
Метод исторического моделирования
Рассчитывается текущая стоимость портфеля, затем рассчитываются все возможные изменения в его стоимости на основе исторических данных и нижний квантиль распределения этих исторических изменений.	Не требует больших объемов исторических данных и знания вероятностного распределения прибылей и убытков портфеля.	Требует значитель­ных затрат времени или специализированного программного обеспечения.
Метод параметрической оценки (вариационно-ковариаци­онная модель)
Строится вектор приращений каждого параметра и историческая ковариационная матрица этих приращений; рассчитывается аппроксимация портфеля для незначительных приращений рынка; измеряется дисперсия портфеля и находится нижний квантиль распределения прибылей и убытков с заданным уровнем доверия.	Самый быстрый. Позволяет решать задачи оптимизации портфеля. Допускает использование экспертных оценок.	Необходимо знание распределения краткосрочных при­­ра­щений рыно­ч­ных показателей и стоимости портфеля.
Метод имитационного моделирования Монте-Карло
Используя совместное распределение приращений рыночных показателей, случайным образом строится множество сценариев и оценивается портфель для каждого из них. В результате получается аппроксимация распределения конечной стоимости портфеля, чей нижний квантиль является оценкой VaR.	Возможен выбор оригинальной функции совместного распределения факторов и объединение конфиденциальной информации и исторических наблюдений.	Необходимо знание совместного распределения фак­торов и использование специального программного обеспечения.

Примечание – Источник: разработка автора.


Полученные результаты дают основание сконцентрировать исследовательскую область решения проблем оптимизации и управления портфелем на многопериодном стохастическом подходе и возможностях динамического программирования. На этом основании автором предложено усовершенствование методического подхода к оценке рисков портфеля, объединяющее соответствующие позиции методик определения размера возможных убытков. Суть предложенного подхода состоит в том, что он позволяет разработать алгоритм решения задачи оптимизации портфеля с учетом начальных требований инвестора. Алгоритм построен на том, что при моделировании поведения инвестора в условиях слабо структурированного целевого рынка в ряду ранжируемых факторов придается больший вес фактору вероятности убытка по отношению к фактору неустойчивости дохода ценных бумаг. Это позволяет согласовать предпочтения инвестора по надежности вложений в рисковой среде с целевой установкой максимизации дохода. Предложенный подход в диссертационной работе определил путь решения исследовательской задачи управления портфелем ценных бумаг на основе многопериодных стохастических моделей.

В главе 2 «Экономико-математическое обеспечение процесса управления портфелем ценных бумаг на основе многопериодных стохастических моделей» разработано методологическое и методическое обеспечение процесса оптимизации и управления портфелем ценных бумаг.

Автором разработан комплекс многопериодных стохастических моделей оптимизации портфеля ценных бумаг, позволяющих дифференцировать методы измерения и ограничения риска в зависимости от длины горизонта инвестирования. В отличие от постановки оптимизационной задачи Марковица, в предложенных моделях нашли отражение фактор непрерывного изменения динамических характеристик рынка и принцип максимального сохранения вложенного капитала инвестора.

Для определения целевой функции и ограничений в оптимизационных моделях использованы уравнения динамики активов модели Блека-Шоулза:





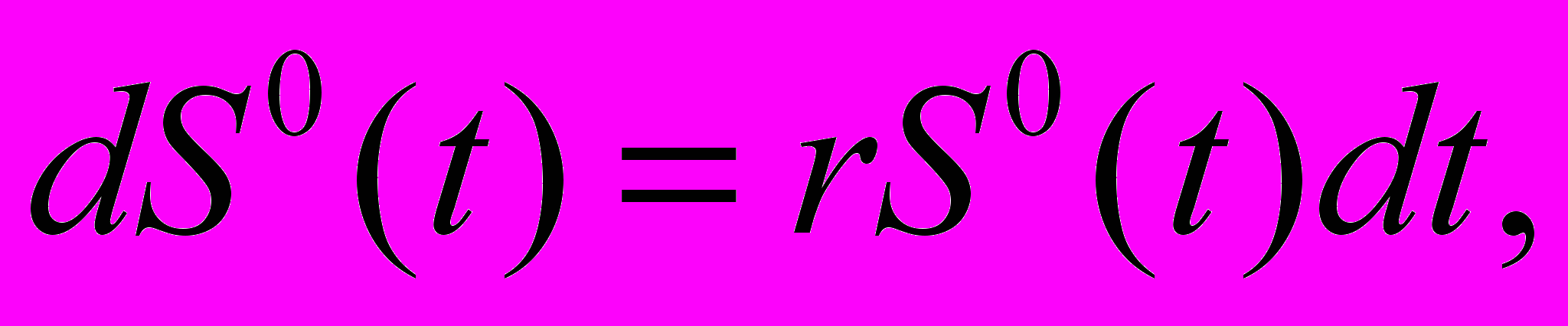
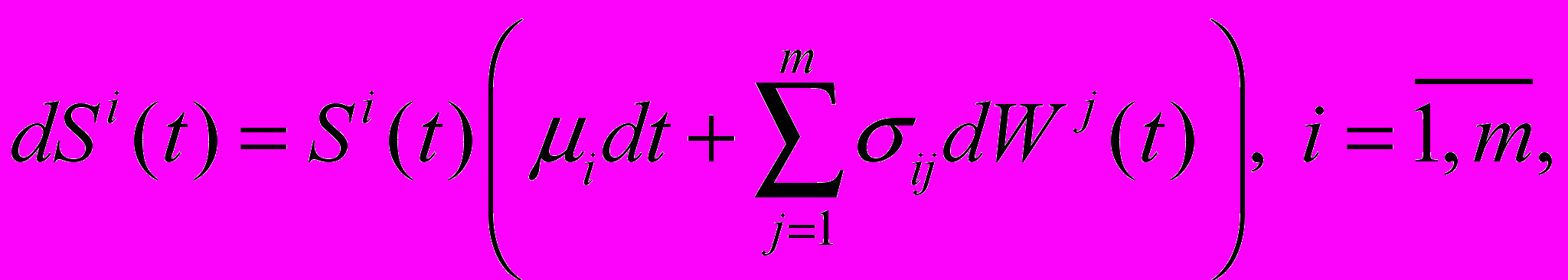
где 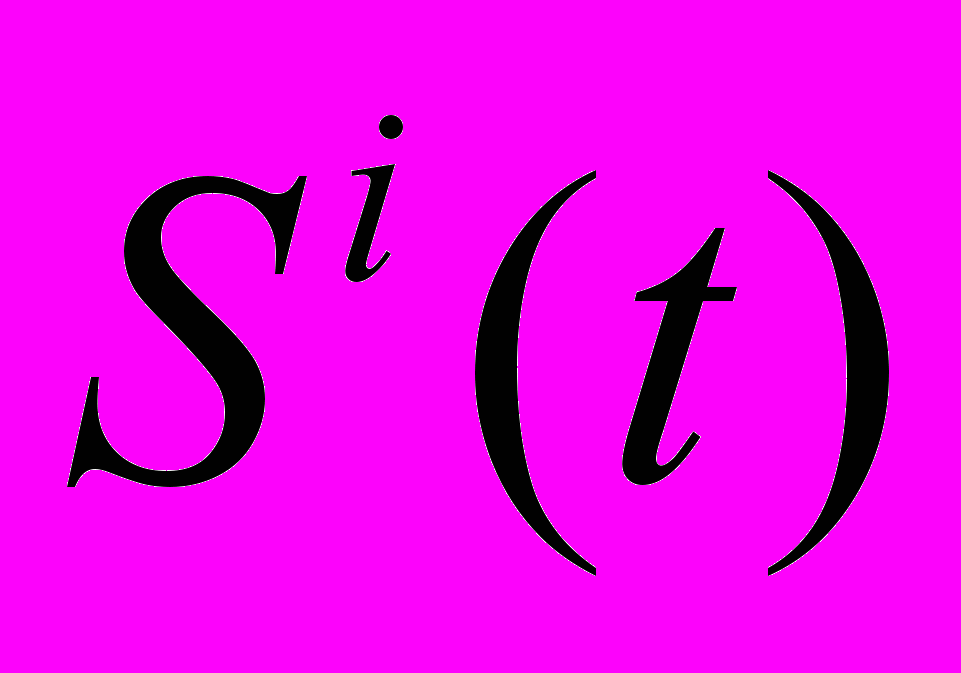, – цена портфельного актива i;

r – безрисковая доходность;

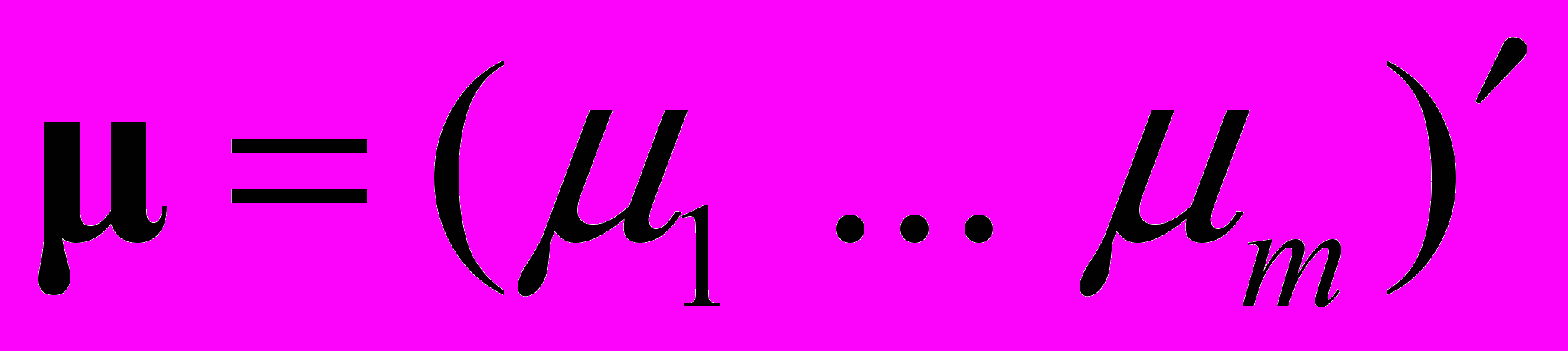– ожидаемые доходности активов;

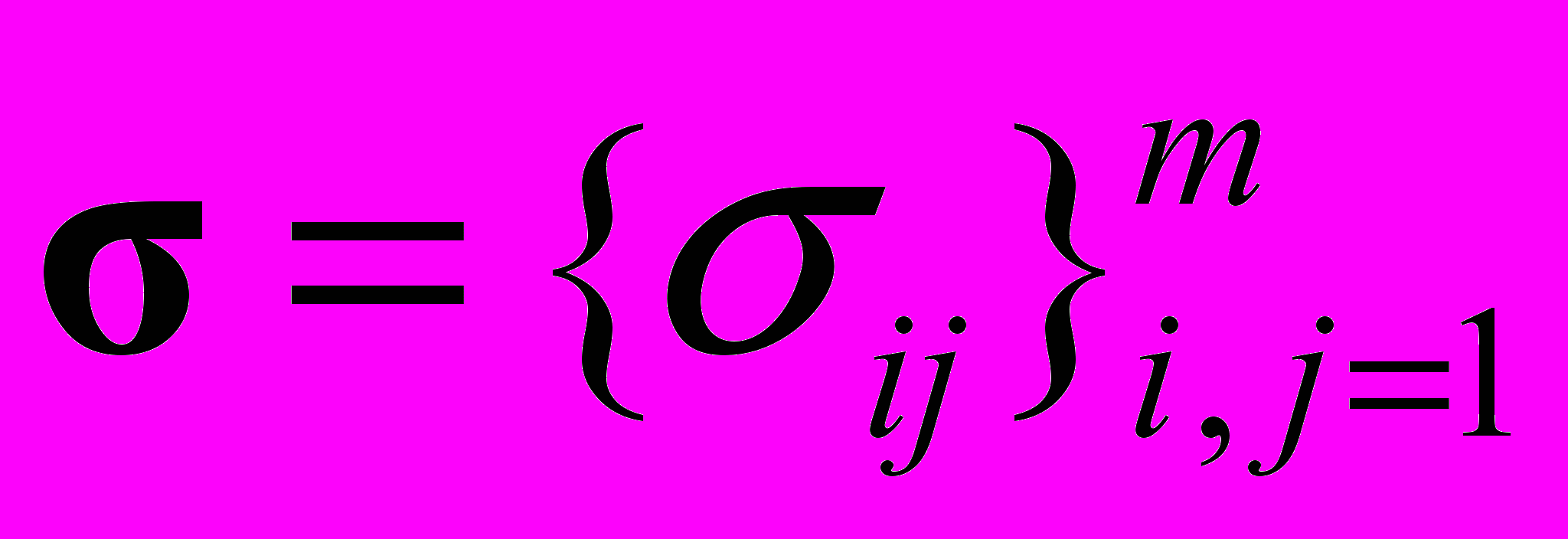– матрица волатильности;

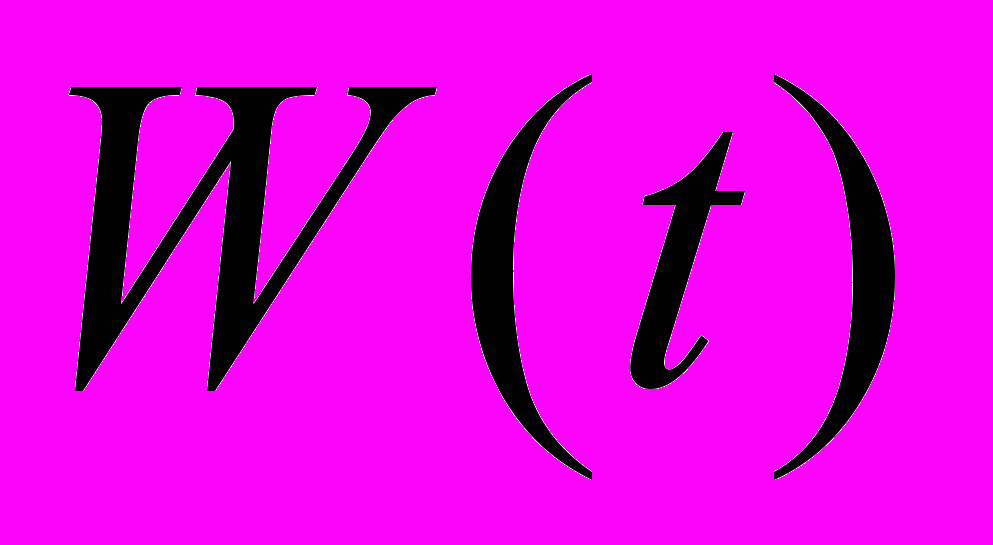– винеровский процесс.

Уравнения и адаптированы для получения базового уравнения динамики стоимости портфеля 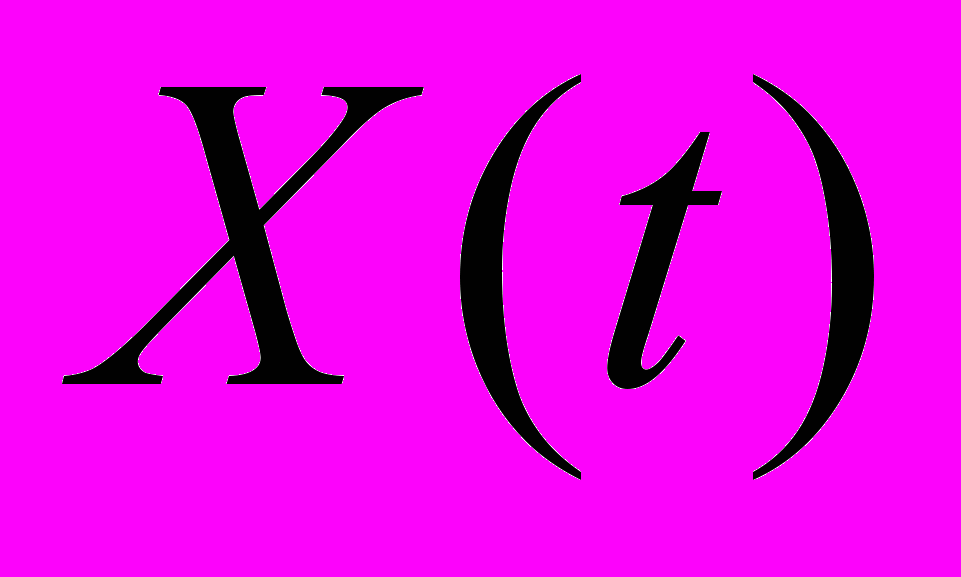и расчета его ожидаемого дохода в конце горизонта инвестирования, который является целевой функцией оптимизационной задачи:



где 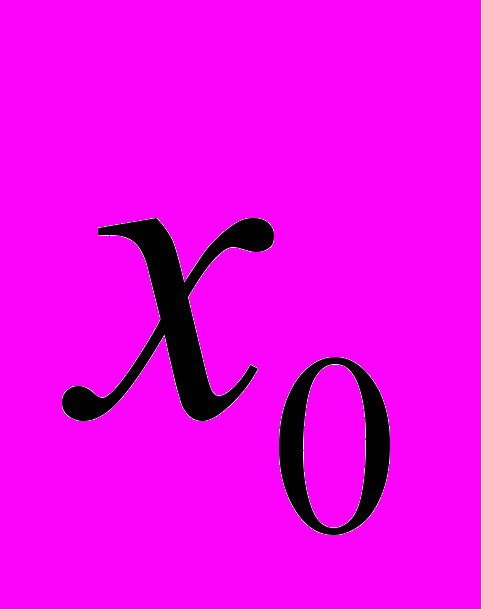– стартовый капитал инвестора;

Т – горизонт инвестирования;

– стратегия инвестора (доли каждого актива в портфеле);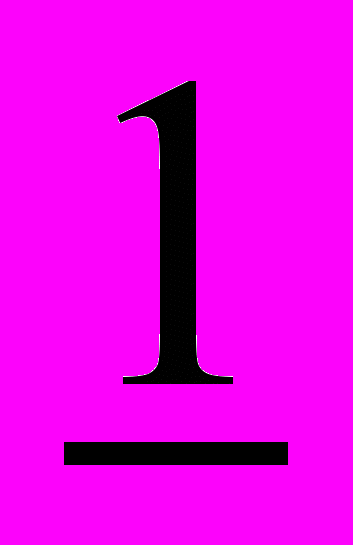

– единичный вектор.

Условие определения оптимальной структуры портфеля – достижение максимальной ожидаемой стоимости портфеля 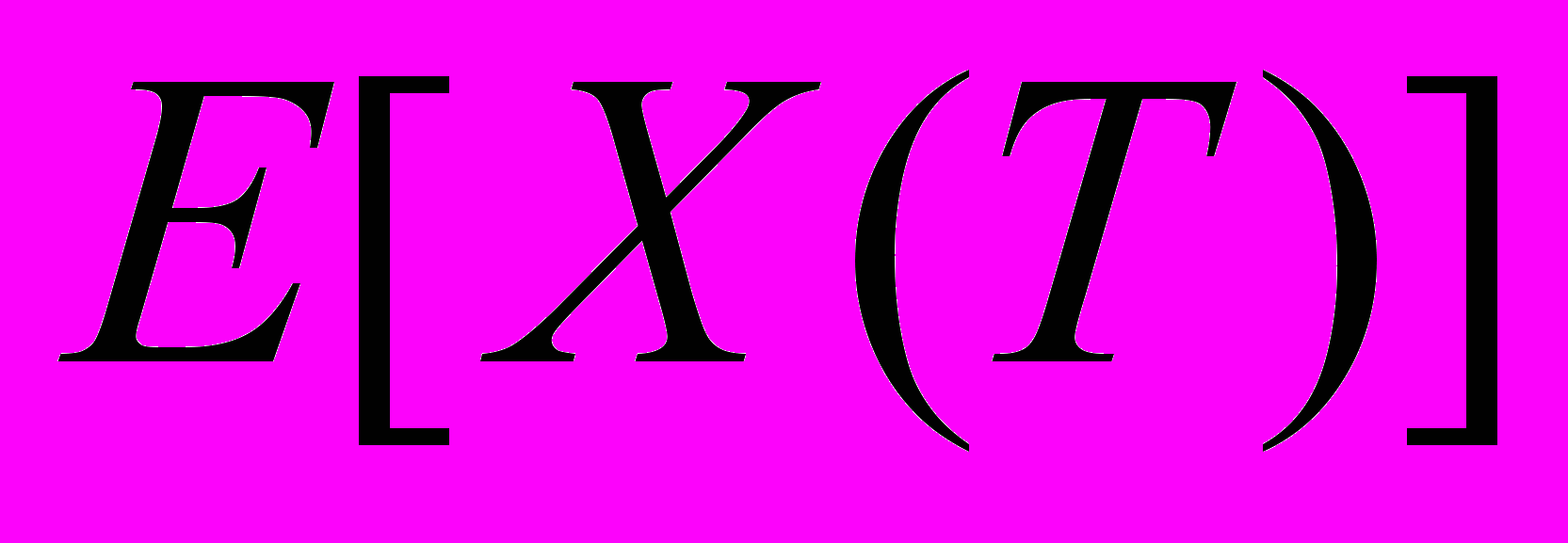в конце горизонта инвестирования при условии, что максимальная сумма потерь стоимости портфеля от изменения цен входящих в него активов, допускаемая инвестором с вероятностью (1 – α), представляет собой сумму С в валюте. Допустимый уровень риска может варьироваться в зависимости от целей инвестора, его отношения к риску, а также от нормативных требований (что особенно актуально для портфеля ценных бумаг коммерческого банка). В качестве мер риска портфеля в моделях предлагается использовать два показателя для краткосрочного и среднесрочного горизонта инвестирования – CVaR и CCaR. CVaR представляет собой возможные потери портфеля, а CCaR – резерв капитала в безрисковых ценных бумагах, необходимый для покрытия возможных потерь. Их основное преимущество заключается в том, что при измерении риска учитываются не только ожидаемые и неожиданные потери, но и «хвосты» распределения потерь, то есть маловероятные, возможные при некотором стечении обстоятельств, потери. Эти показатели построены автором на базе методологии VaR и концепции максимального убытка, рекомендованных Базельским комитетом по банковскому надзору в качестве обязательных компонентов системы риск-менеджмента финансовых организаций.

Ограничение риска в задаче оптимизации портфеля с краткосрочным горизонтом инвестирования имеет вид (CVaR-модель):



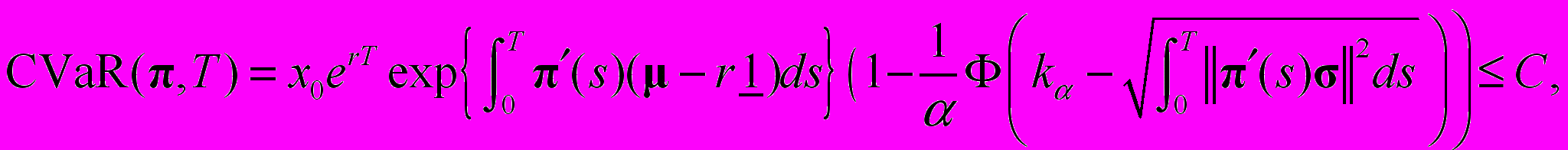
со среднесрочным горизонтом инвестирования (CСaR-модель):



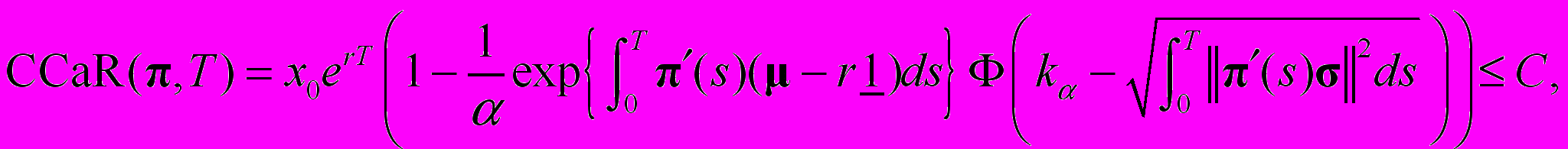
где 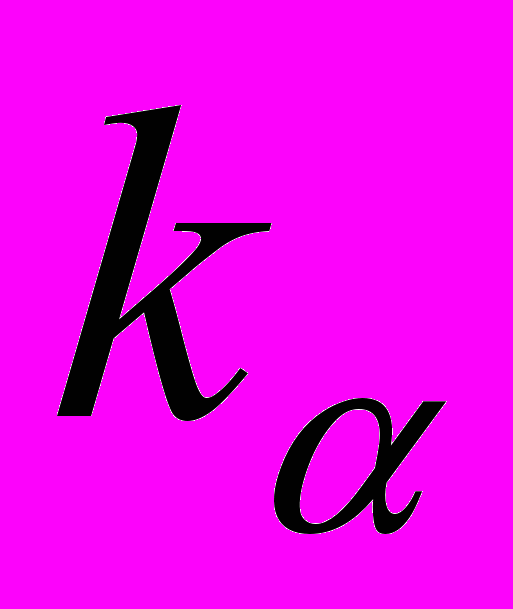– наименьшее возможное с вероятностью (1 – α) значение случайной величины, имеющей стандартное нормальное распределение, α-квантиль.

Предлагаемая автором дифференциация моделей по срокам владения портфелем базируется на проведенном исследовании особенностей функционирования современного рынка ценных бумаг. Так, вложения в акции на средне- и долгосрочных горизонтах инвестирования приносят больший доход, чем инвестиции в безрисковые активы. Вместе с тем, по мере возрастания срока владения возрастает и неопределенность получения дохода, а значит и разрыв между ожидаемой и наименьшей возможной стоимостью портфеля, что приводит к росту CVaR. Поэтому при оптимизации портфеля с таким ограничением риска оптимальная доля безрисковой бумаги будет неоправданно большой, что противоречит реалиям рынка. В свою очередь показатель CCaR с ростом горизонта инвестирования уменьшается, так как в расчет принимается разница между стоимостью безрискового портфеля со сравнительно низкой доходностью и наименьшей возможной стоимостью рискового портфеля.

Если в портфеле присутствуют помимо первичных производные ценные бумаги (в исследовании автором рассматривались американские колл-опционы), к вышеуказанным параметрам оптимизационной задачи прибавляется дополнительная характеристика – функция, определяющая стоимость дериватива в каждый конкретный момент времени в зависимости от цены и срока исполнения. Из-за нелинейного характера этой функции прямой расчет ожидаемого дохода и риска портфеля невозможен. В то же время анализ уравнения динамики портфеля, построенного путем реплицирования опциона, позволил установить, что оптимальное решение задачи для портфеля с опционами представляет собой решение задачи для портфеля базовых активов, скорректированное на дельту опциона. При этом сумма возможных потерь от использования выбранной структуры портфеля в конце горизонта инвестирования определяется также показателем CVaR для краткосрочного или CCaR для среднесрочного портфеля.

Предлагаемый комплекс многопериодных стохастических моделей оптимизации портфеля, а также формализованная автором типовая последовательность процесса формирования и управления портфелем, позволили разработать инструментальный метод управления портфелем ценных бумаг, алгоритм которого (рисунок 1) включает следующие этапы:

1) Постановка задачи: выбор активов, стартового капитала, инвестиционного горизонта, приемлемого уровня риска.

2) Выбор модели в зависимости от длины инвестиционного горизонта и типа входящих в портфель активов.

3) Оценка параметров выбранной модели на основе имеющихся данных: безрисковой ставки; ожидаемых доходностей акций; волатильностей; ковариационной матрицы.

4) Решение задачи оптимизации с заданными параметрами: нахождение оптимальной доли каждого актива в портфеле – оптимальной структуры.

5) Управление структурой портфеля: сравнение текущей структуры портфеля с оптимальной и, при необходимости, покупка/продажа активов по текущим рыночным ценам исходя из полученного на предыдущем этапе решения задачи оптимизации – определенной суммы вложения в каждый актив.



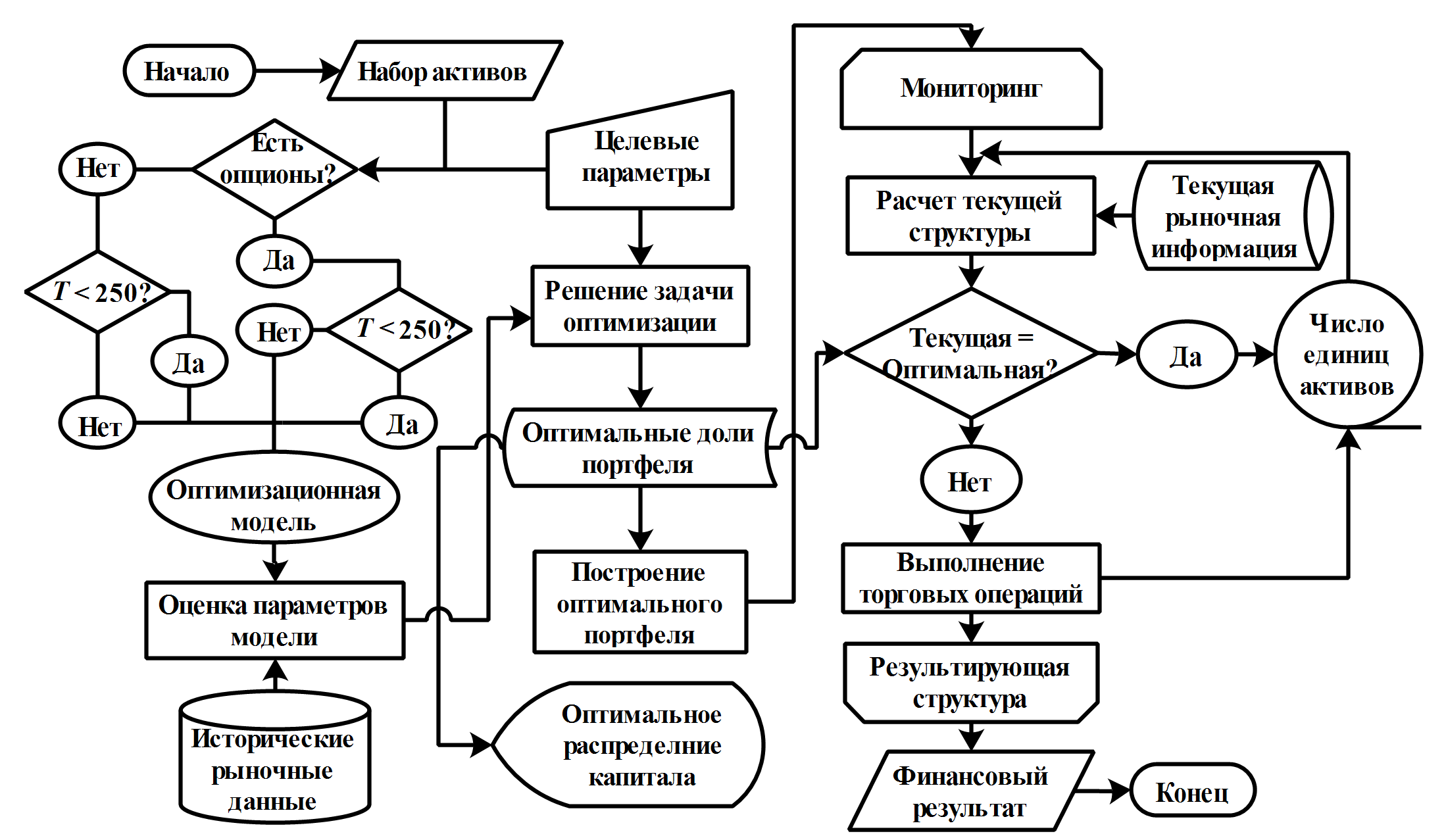
Рисунок 1 – Алгоритм практической реализации инструментального
метода управления портфелем ценных бумаг


Примечание – Источник: разработка автора.


В главе 3 «Прикладные методики и алгоритмы управления портфелем ценных бумаг» предложены методы реализации разработанной модельной системы и апробирован алгоритм практической реализации инструментального метода управления портфелем ценных бумаг.

Предложенное автором решение двух типов задач оптимизации портфеля ценных бумаг с различными ограничениями на уровень риска сводится к математическому алгоритму реализации процедуры введения α-квантиля будущей стоимости портфеля инвестора в граничное условие. Это позволяет получить аналитическую разработку ситуации в условиях непрерывного времени, пригодную для соответствующего структурирования портфеля. Существующие в настоящее время методы решения подобных задач строятся на сложном математическом аппарате, который практически невозможно адаптировать к требованиям текущей инвестиционной деятельности. Автором впервые предложена прикладная разработка динамической задачи, которая путем сочетания инструментальных возможностей метода СVaR-СCaR и средств системы Mathematica позволяет получить оптимальную структуру портфеля на каждый момент времени при заданном уровне ограничений.

Автором предложен алгоритм решения оптимизационной задачи с использованием наиболее распространенного типа производных ценных бумаг (опционов). Решение осуществлено в соответствии с процедурой реплицирования по методу Р. Корна – заменой стоимости опциона стоимостью портфеля из базового актива и безрискового. Такой подход позволил устранить проблему описания нелинейной динамики портфеля, содержащего производные ценные бумаги. В предложенном решении осуществлена интеграция оптимизационных решений портфеля базовых активов и опционного портфеля. Предложенное автором решение развивает математический аппарат опционного моделирования и адаптирует его к практической деятельности на рынке ценных бумаг. Это позволяет снять проблему дополнительного страхования риска инвестирования и дает экономию средств инвестора на специальных страховых премиях.

Для реализации схемы оптимизации портфеля ценных бумаг в рамках предложенного инструментального метода автором разработано модульное приложение в системе Mathematica, позволяющее автоматизировать расчет оптимальных долей портфельных активов относительно заданных инвестором параметров и оперативно получать таблицу распределения капитала. Тестирование предложенного инструментального модуля на реальном рынке показало, что он снижает затраты рабочего времени на принятие инвестиционных решений, тем самым повышая эффективность управления портфелем ценных бумаг в режиме реального времени.

Предложенный в данной работе инструментальный метод управления портфелем ценных бумаг на основе многопериодных стохастических моделей выбора оптимального размещения в финансовые инструменты базируется на входных параметрах, представляющих собой статистические показатели, расчет которых производится на основе статистических выборочных оценок исторических рядов рыночных данных. Следовательно, значения параметров и результаты использования моделей зависят от длины исторических рядов, которые выбраны для расчета. Вследствие этого при практической реализации предлагаемых методик возникает необходимость аргументированного выбора длины рядов исторических данных. Для решения данной проблемы предлагается в качестве используемой длины исторических рядов выбирать такую длину, расчет оптимального портфеля на основе которой давал в предшествующие периоды наибольшую доходность инвестиций. Её значение может быть получено путем моделирования ситуаций построения оптимального портфеля в прошлом по различным вариантам длин рядов логарифмических доходностей и расчета прибылей и убытков, получаемых от использования этих портфелей.

Практические методики на базе разработанного алгоритма протестированы на примере управления портфелями российских ценных бумаг. Проведена серия аналогичных экспериментов, включающих расчет оптимальной структуры портфеля с применением динамического модуля и выявление результатов использования данной структуры на реальном рынке в случае реализации динамической (в течение горизонта инвестирования осуществлялся мониторинг текущей структуры портфеля и при необходимости проводились операции купли-продажи ценных бумаг для восстановления оптимальной структуры) и статической (торговые операции в течение горизонта инвестирования не проводились) торговых стратегий.

Проиллюстрируем предлагаемый подход на примере. Пусть 5 октября 2010 г. инвестор располагает суммой в размере 100 000 RUR для построения оптимального портфеля, включающего банковский денежный счет с доходностью 3% годовых и акции SBER03, URKA, MGNT, ROSN, на один месяц. При этом он готов понести возможный убыток в размере, не превышающем 1% инвестированного капитала (1 000 RUR) с вероятностью 95%. Для выбора необходимой длины исторического ряда, на основе которого производится оценка входных параметров модели, следует провести экспериментальное моделирование использования оптимальной структуры в прошлом. Исходные данные: исторические ряды логарифмических доходностей однодневных вложений в указанные активы за период с 26 ноября 2007 г. по 15 октября 2009 г. Порядок проведения экспериментов: в определенную дату в прошлом рассчитывается оптимальная структура портфеля на основе заданной длины рядов исторических данных. Далее, по истечении месяца от даты построения портфеля определяется сумма прибыли или убытка от использования рассчитанной оптимальной структуры на основе имеющейся реальной информации о курсах активов. Эта сумма является результатом проведения одного эксперимента. Для стандартизации экспериментов предположим, что инвестора интересуют результаты использования рассчитанных оптимальных структур в течение предшествующих 12 месяцев. При этом минимальным значением длины исторического ряда будет величина 20 торговых дней (1 месяц), максимальным значением – 470 торговых дней. Наилучшей длине рядов соответствует максимальная сумма прибылей или убытков за год.

На основе данного экспериментального исследования была разработана программа в системе Mathematica, с помощью которой были произведены расчеты и получены итоговые результаты. Было проведено 10 824
(10 824 = (470 – 20 + 1)×12×2) моделирований использования оптимальных структур на исторических данных. В результате были рассчитаны 902 суммы прибылей и убытков, соответствующие использованию 451 варианта длин рядов исторических данных (от 20 до 470 торговых дней) для двух стратегий. Полученные результаты в графическом виде представлены на рисунке 2.

Динамическая
стратегия





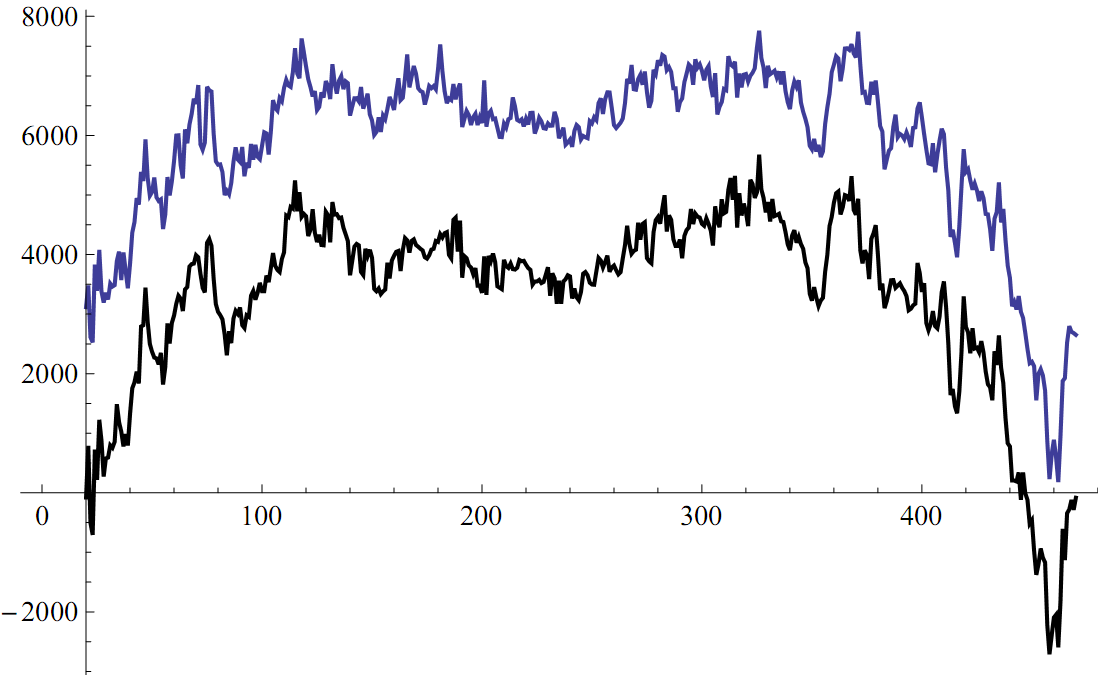
Рисунок 2 – Результаты применения статической и динамической
стратегии управления портфелем на прошлых данных с различными длинами временных рядов

Примечание – Источник: разработка автора.


Сравнительный анализ результатов показал, что характер зависимости получаемой прибыли от длины исторических рядов для обеих стратегий практически совпадает. Максимальная прибыль (7 760.57 RUR для динамической стратегии, 5 679.61 RUR для статической) была получена при значении длины ряда, равном 326 торговым дням. Следовательно, эта длина является наилучшим выбором для расчета статистических параметров модели, что может служить основанием для использования инвестором исторического периода данных такой же длины при текущем расчете оптимальной структуры портфеля. При этом прибыль от реализации статической стратегии приблизительно на 37% ниже прибыли, полученной при использовании динамической стратегии, и такая зависимость прослеживается при сравнении всех остальных результатов. Следовательно, можно сделать вывод о преимуществе последней. Анализ тех периодов, когда использование динамической стратегии давало отрицательные результаты, показал, что средний убыток составил 236.34 RUR, максимальный убыток – 1 347.25 RUR, количество случаев превышения убытком 1 000 RUR – 3. Таким образом, несмотря на то, что эти данные получены при использовании различных длин временных рядов, ограничение уровня потерь 1 000 RUR в реальности было выполнено в 5 409 случаях из 5 412, что свидетельствует о достаточно качественном построении модели.

В таблице 2 представлены некоторые результаты проведенных экспериментов, позволяющие судить о взаимосвязи структуры портфеля с длиной горизонта инвестирования, уровнем риска (процент вложенного капитала, который готов потерять инвестор) и доверительной вероятности.


Таблица 2 – Зависимость структуры портфеля от значений параметров
оптимизационных моделей

Уровень доверия	Уровень риска	Горизонт инвестирования (дни)	Структура капитала (доли)
			Счет	SBER03	URKA	MGNT	ROSN
95%	10%	10	0.4509	0.6411	0.2231	0.7323	–1.0470
99%	10%	10	0.5732	0.4984	0.1735	0.5692	–0.8142
99%	50%	100	0.7365	0.3076	0.1071	0.3514	–0.5026
95%	50%	100	0.6683	0.3873	0.1348	0.4423	–0.6327
95%	80%	280	0.7481	0.2941	0.1024	0.3359	–0.4804
95%	10%	1 150	0.9957	0.0049	0.0017	0.0057	–0.0081
95%	90%	1 150	0.9367	0.0739	0.0257	0.0844	–0.1207

Примечание – Источник: разработка автора.


Следует отметить, что самая высокая ожидаемая годовая доходность у акций MGNT (64%), далее идут SBER03 (48.7%) и ROSN (22.3%), самая низкая – у URKA (–9%). Поэтому в структуре рисковых активов доля MGNT для любых значений параметров самая большая, а доля URKA самая маленькая. При этом акция ROSN очень сильно коррелирует с SBER03 и URKA (79% и 67% соответственно), и короткая продажа данного актива позволяет застраховать инвестора от потерь в результате падения стоимости последних. Основываясь на сравнительном анализе результатов, представленных в таблице 2, можно говорить о том, что чем выше доверительная вероятность, тем больше доля безрискового актива в портфеле. Также последняя возрастает при увеличении горизонта инвестирования и при снижении величины вложенного капитала, который готов потерять инвестор.