Geum.ru

1. Классификация моделей представления знаний

Вид материалаДокументы

Содержание


28. Этапы развития научного направления “мягкие вычисления”.
Постановка задачи оптимизации, теорема Вейерштрасса, понятие минимума.
27. Язык CLIPS. Основные элементы и конструкцию.
26. Язык ПРОЛОГ. Основные элементы и конструкции.
Математическое определение лингвистической переменной
Пример: Рассмотрим лингвистическую переменную, описывающую возраст человека, тогда: x
20. Сетевые модели представления знаний.
Нечеткие множества и операции с ними
Операции над нечёткими множествами
15. Данные и знания. Основные отличия.
51. Гибридные системы.
13. Фреймы и их применение в экспертных системах.
9. Система опровержений на основе резолюций.
5. Предикаты первого порядка. Основные определения и понятия.
Логика первого порядка
4. Методы структурирования и формализации знаний.
U- область, на которой определены значения лингвистической переменной; 6
29. Генетические алгоритмы.
Применение генетических алгоритмов
6. Модели представления знаний. Историческая справка.
...
Полное содержание
Подобный материал:
  1   2   3   4   5   6   7   8   9   ...   12






1.Классификация моделей представления знаний.


В настоящее время разработано множество моделей представления знаний. Имея обобщенное название, они различаются по идеям, лежащим в их основе, с точки зрения математической обоснованности. Типы моделей показаны на рисунке.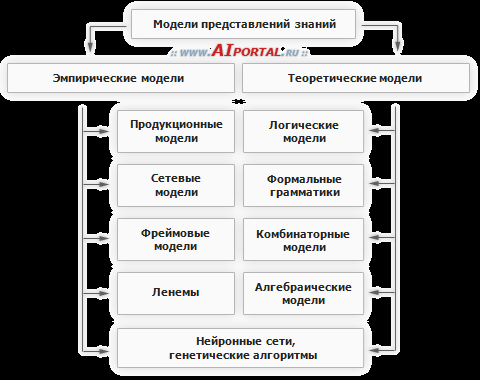





Первый подход, называемый эмпирическим, основан на изучении принципов организации человеческой памяти и моделировании механизмов решения задач человеком. На основе этого подхода в настоящее время разработаны и получили наибольшую известность следующие модели:
  • продукционные модели – модель основанная на правилах, позволяет представить знание в виде предложений типа: «ЕСЛИ условие, ТО действие». Продукционная модель обладает тем недостатком, что при накоплении достаточно большого числа (порядка нескольких сотен) продукций они начинают противоречить друг другу;
  • сетевые модели (или семантические сети) – в инженерии знаний под ней подразумевается граф, отображающий смысл целостного образа. Узлы графа соответствуют понятиям и объектам, а дуги – отношениям между объектами. Обладает тем недостатком, что однозначного определения семантической сети в настоящее время отсутствует;
  • фреймовая модель – основывается на таком понятии как фрейм (англ. frame – рамка, каркас). Фрейм – структура данных для представления некоторого концептуального объекта. Информация, относящаяся к фрейму, содержится в составляющих его слотах. Слоты могут быть терминальными либо являться сами фреймами, т.о. образуя целую иерархическую сеть.

Более подробно эти модели рассматриваются в соответствующих статьях. Условно в группу эмпирического подхода можно включить нейронные сети и генетические алгоритмы, относящиеся к бионическому (основано на предположении о том, что если в искусственной системе воспроизвести структуры и процессы человеческого мозга, то и результаты решения задач такой системой будут подобны результатам, получаемым человеком) направлению искусственного интеллекта. Особенностью моделей этого типа является широкое использование эвристик, что в каждом случае требует доказательства правильности получаемых решений.

Второй подход можно определить как теоретически обоснованный, гарантирующий правильность решений. Он в основном представлен моделями, основанными на формальной логике (исчисление высказываний, исчисление предикатов), формальных грамматиках, комбинаторными моделями, в частности моделями конечных проективных геометрий, теории графов, тензорными и алгебраическими моделями. В рамках этого подхода до настоящего времени удавалось решать только сравнительно простые задачи из узкой предметной области.


28. Этапы развития научного направления “мягкие вычисления”.


Термин "мягкие вычисления" введен Лофти Заде в 1994 году. Это понятие объединяет такие области как: нечеткая логика, нейронные сети, вероятностные рассуждения, сети доверия и эволюционные алгоритмы; которые дополняют друг друга и используются в различных комбинациях или самостоятельно для создания гибридных интеллектуальных систем. Поэтому создание систем работающих с неопределенностью, надо понимать как составную часть "мягких" вычислений.

По существу в 1970 году Л.Заде был создан новый метод вычислительной математики, который был поддержан аппаратными средствами (нечеткими процессорами) который в ряде проблемных областей стал более эффективным, чем классические методы. Первоначально эти области входили в проблематику искусственного интеллекта. Постепенно круг этих областей существенно расширился и сформировалось направление "вычислительного интеллекта". В это направление в настоящее время входят:
  • нечеткая логика и теория множеств;
  • нечеткие экспертные системы;
  • системы приближенных вычислений;
  • теория хаоса;
  • фрактальный анализ;
  • нелинейные динамические системы;
  • гибридные системы (нейронечеткие или нейрологические, генетиконейронные, нечеткогенетические или логикогенетические системы);
  • системы, управляемые данными (нейронные сети, эволюционное вычисление).

Постановка задачи оптимизации, теорема Вейерштрасса, понятие минимума.


Пусть задана функция q(x), определенная во всех значениях x принадлежащих X. В общем случае x может быть вектором значений многопараметрической функции q(x).

Тогда, в общей задаче оптимизации требуется найти вектор x=(x1,x2,...,xn) из допустимой области X, который обращает в минимум целевую функцию q(x). Если необходимо найти максимум функции, то в качестве целевой берут обратную функцию -q(x).

Теорема Вейерштрасса. Непрерывная функция, определенная на непустом замкнутом ограниченном множестве, достигает своего минимума (максимума) по крайней мере в одной из точек этого множества.

В общем случае глобальный минимум в точке x' области определения X характеризуется:

q(x')<=q(x) для всех x принадлежащих X

Знак '<=' предполагает возможность существования нескольких минимумов. При таком определении глобальный минимум называют слабым.

Сильный глобальный минимум определяется:

q(x')
Минимум в точке x=x' называют локальным (относительным), если найдется такая окрестность O(x') точки x', что для всех x принадлежащих O(x') имеет место q(x')<=q(x)


27. Язык CLIPS. Основные элементы и конструкцию.

CLIPS, (от ссылка скрыта C Language Integrated Production System) — ссылка скрыта среда для разработки ссылка скрыта. ссылка скрыта и название предложены ссылка скрыта (Charles Forgy) в ссылка скрыта (Official Production System). Первые версии CLIPS разрабатывались с ссылка скрыта в Космическом центре Джонсона (ссылка скрыта), ссылка скрыта (как альтернатива существовавшей тогда системе ссылка скрыта), пока в начале ссылка скрыта не было приостановлено финансирование, и NASA вынудили купить ссылка скрыта продукты.

Вероятно, CLIPS является наиболее широко используемой инструментальной средой для разработки экспертных систем благодаря своей скорости, эффективности и бесплатности. Несмотря на то, что теперь она являетсяссылка скрыта, она до сих пор обновляется и поддерживается своим изначальным автором, Гэри Райли (Gary Riley).

CLIPS включает полноценный ссылка скрыта язык COOL для написания экспертных систем. Хотя она написана на языке ссылка скрыта, её интерфейс намного ближе к языку программирования ссылка скрыта. Расширения можно создавать на языке Си, кроме того, можно интегрировать CLIPS в программы на языке Си. Как и другие экспертные системы, CLIPS имеет дело с правилами и фактами. Различные факты могут сделать правило применимым. Применимое правило затем допускается (ссылка скрыта). ссылка скрыта и правила создаются предварительным объявлением, как показано в примере:

(deffacts trouble_shooting

(car_problem (name ignition_key) (status on))

(car_problem (name engine) (status wont_start))

(car_problem (name headlights) (status work))

)

(defrule rule1

(car_problem (name ignition_key) (status on))

(car_problem (name engine) (status wont_start))

=>

(assert (car_problem (name starter) (status faulty))

)

Потомками CLIPS являются языки программирования ссылка скрыта (часть CLIPS, работающая с правилами и переписанная на ссылка скрыта, позже развившаяся в другом направлении), ссылка скрыта, ссылка скрыта, ссылка скрыта (с добавлением концепции значимости relevancy в язык) и другие. Существует учебник для ссылка скрыта, Expert Systems: Principles and Programming (ссылка скрыта) и книга по Jess, Jess in Action: Rule Based Systems in Java (ссылка скрыта). Кроме того CLIPS содержит обширную документация прямо в поставке.Существующие верcии CLIPS для Windows (clipswin.exe) не поддерживают кириллицу (консольная версия CLIPS clipsdos.exe поддерживает только кириллицу в формате UTF-8). В сети Интернет можно найти русифицированную версию CLIPS для Windows, поддерживающую кириллицу в формате ANSI, но она распространяется без исходных кодов и имеет ряд проблем с отображением символов в Windows XP. Именно отсутствие полноценной поддержки кириллицы и является основной причиной слабого распространения CLIPS в России. При компиляции из исходников возможно пропатчить их, добавив поддержку koi8-r.


26. Язык ПРОЛОГ. Основные элементы и конструкции.

Пролог (ссылка скрыта Programmation en Logique) — язык и система ссылка скрыта, основанные на языке предикатов математической логики ссылка скрыта, представляющей собой подмножество ссылка скрыта.

Основными понятиями в языке Пролог являются факты, правила логического вывода и запросы, позволяющие описывать ссылка скрыта, процедуры логического вывода и принятия решений.

Факты в языке Пролог описываются логическими предикатами с конкретными значениями. Правила в Прологе записываются в форме правил логического вывода с логическими заключениями и списком логических условий.

Особую роль в интерпретаторе Пролога играют конкретные запросы к базам знаний, на которые система логического программирования генерирует ответы «истина» и «ложь». Для обобщённых запросов с переменными в качестве аргументов созданная система Пролог выводит конкретные данные в подтверждение истинности обобщённых сведений и правил вывода.

Факты в базах знаний на языке Пролог представляют конкретные сведения (знания). Обобщённые сведения и знания в языке Пролог задаются правилами логического вывода (определениями) и наборами таких правил вывода (определений) над конкретными фактами и обобщёнными сведениями.

Начало истории языка относится к 1970-м годам.[1] Будучи ссылка скрыта, Пролог воспринимает в качестве программы некоторое описание задачи или баз знаний и сам производит логический вывод, а также поиск решения задач, пользуясь механизмом ссылка скрыта и унификацией.