1. Классификация моделей представления знаний
| Вид материала | Документы |
- Экспертные системы и базы знаний, 42.45kb.
- Знаний. Модели представления знаний: логическая, сетевая, фреймовая, продукционная, 215.44kb.
- Системы искусственного интеллекта, 15.16kb.
- Техническое задание на выполнение курсовой работы на тему: Исследование моделей представления, 32.74kb.
- Судомоделирование, 131.6kb.
- План изучения дисциплины № п/п, 155.57kb.
- Лекции по дисциплине «Математическое моделирование» для студентов и магистрантов специальности, 21.92kb.
- 2. Лекция: Системы представления знаний, 171.88kb.
- Программа по курсу " Моделирование систем управления, 30.71kb.
- Программа курса «экономика труда», 585.26kb.
Модель предметной областиПостроение информационных систем так или иначе упирается в проблемы информационного обмена. Информационный обмен -- это процесс, в который вовлечены отправитель и получатель (или адресат), соединенные надежным каналом связи, и который заключается в передаче сообщения от отправителя к получателю по каналу связи. В трудах одного из основателей теории информации А.Н. Колмогорова говорится: ``Информация есть характеристика не сообщения, а соотношения между сообщением и его потребителем. Без наличия потребителя, хотя бы потенциального, говорить об информации бессмысленно''. Согласно этой характеристике: ``Информация -- это то, что изменяет представление (знание) ее получателя о чем-либо''. Таким образом, использование информации упирается в понятия ``знание'' в некоторой предметной области. Предметная область -- часть реального мира, рассматриваемая в пределах данного контекста. Под контекстом здесь может пониматься, например, область исследования или область, которая является объектом некоторой деятельности. Дадим основные определения. Определение Ориентированный помеченный граф -- это тройка 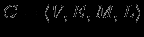 , где , где 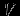 -- множество вершин, -- множество вершин, 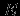 -- множество дуг -- множество дуг 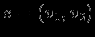 из вершины из вершины 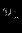 в вершину в вершину 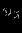 , , 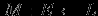 -- функция разметки дуг, которая каждой дуге сопоставляет элемент из множества меток -- функция разметки дуг, которая каждой дуге сопоставляет элемент из множества меток 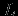 . .Определение. Понятийная модель предметной области -- совокупность понятий (концептов, терминов) и отношений между ними, которым соответствуют сущности из реального мира, реализованная в виде ориентированного помеченного графа 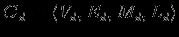 , у которого любая метка также является вершиной: , у которого любая метка также является вершиной: 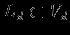 . Здесь каждая вершина является понятием; каждая дуга из вершины . Здесь каждая вершина является понятием; каждая дуга из вершины 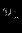 в вершину в вершину 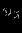 с меткой с меткой 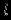 описывает отношение описывает отношение 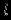 понятия понятия 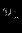 к понятию к понятию 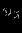 . Таким образом, любое отношение является понятием. . Таким образом, любое отношение является понятием.Определение Содержательную модель предметной области для понятийной модели 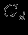 -- ориентированный помеченный граф -- ориентированный помеченный граф 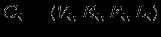 , для которого выполнены следующие условия: , для которого выполнены следующие условия:
Вершины графа содержательной МПО мы будем называть информационными элементами. Определение Модель предметной области (МПО) есть объединение графов понятийной и содержательной моделей предметной области: 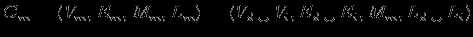 , где , где 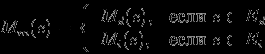
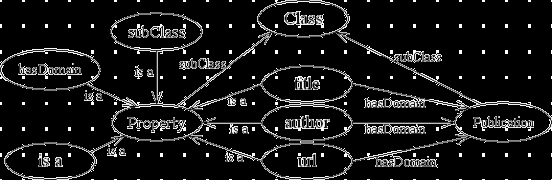
Данное определение МПО выделяет две ее составляющих: понятийную и содержательную (рис. 5). Понятийная часть определяет концепты, термины предметной области и отношения между ними. Еще раз отметим, что любое отношение также должно быть концептом, который может находиться в отношениях с другими концептами (рис. 6). Понятийная МПО является базовым звеном в работе с информацией, поскольку она определяет ``каркас'', на который крепится содержательная составляющая. Информационные элементы содержательной МПО соответствуют реальным объектам предметной области. Отношения, описываемые терминами понятийной МПО, можно разделить на два типа: содержательные и понятийные. Содержательные определяют отношения одного информационного элемента к другому, а понятийные -- отношения элемента к концепту из понятийной МПО. Несмотря на то, что графовая структура МПО ограничивает нас использованием только бинарных отношений, это не оказывает существенного влияния на выразительность моделирования, поскольку, очевидно, любое n-арное отношение может быть представлено в виде нескольких бинарных отношений.
Определение Семантическая информация 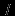 -- подграф модели предметной области. -- подграф модели предметной области.Действительно, согласно определению информация изменяет МПО ее получателя. Значит, информации можно сопоставить измененный фрагмент МПО, который и был назван семантической информацией. Заметим, что в этом определении не используется тезис об информации, как о соотношении между сообщением и потребителем, поскольку при разработке информационных систем необходимо говорить об информации не только с точки зрения ее потребителя, но и с точки зрения ее отправителя. Следует ожидать, что оба они обладают собственными МПО, при этом нередко отправитель не имеет или имеет неполные сведения о МПО получателя. Поэтому отправитель информации может рассматривать ее только в рамках собственной МПО. Аналогично, МПО получателя информации может быть не согласована с МПО отправителя, и получатель сможет ``понять'' только какую-то ее часть, что соответствующим образом отразиться в его МПО. Таким образом, исходному понятию ``информация'' в рамках описываемой модели информационного обмена будет сопоставлен термин ``интерпретация информации'' -- семантическая информация, полученная в результате информационного обмена (рис. 7): Определение Интерпретация семантической информации 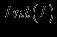 -- это семантическая информация, полученная адресатом в результате информационного обмена, в котором отправителем была послана семантическая информация -- это семантическая информация, полученная адресатом в результате информационного обмена, в котором отправителем была послана семантическая информация 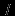 . .
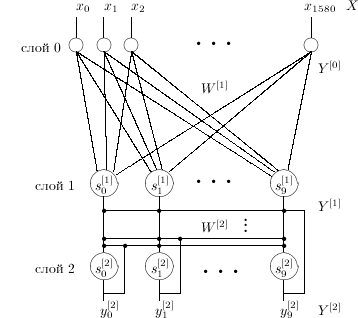
Существует 2 направления: нейрокибернетика и кибернетика черного ящика Нейрокибернетики взяли за основу структуру и принципы функционирования единственного созданного природой устройства, способного рассуждать, – мозга. Клетки мозга называются нейронами, отсюда и название направления. Ученые считают, что, смоделировав мозг, смогут воссоздать и его работу. Исследователи направления «кибернетика черного ящика» придерживались мнения, что не важно, по каким принципам работает устройство, какие средства и методы лежат в его основе, главное – имитировать функции мозга, даже если кроме результата это не будет иметь ничего общего с естественным разумом. 33. Исчисление предикатов. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ - раздел математической логики, логическое исчисление, в алфавит знаков которого, помимо символов исчисления высказываний, входят также символы вещей (индивидов), их свойств и отношений, а также выражений "все" и "некоторые" (кванторы), позволяющие количественно охарактеризовать связи вещей, свойств и отношений; служит аксиоматизацией логики предикатов. 36. Нейронная сеть Хемминга. Искусственная нейронная сеть Хемминга (рис.1) была предложена в 1987 г. Р. Липманом [1,2]. Она представляет собой сеть с двумя обрабатывающими слоями: первый слой - слой Хемминга, второй слой - немного изменённая сеть Хопфилда.
На вход нейронной сети подаётся картинка в формате BMP, размером 17 x 31 точек, представляющая собой матрицу 51 x 31 байт, таким образом входной (или распределительный) слой сети (слой 0 на рис.1) состоит из 51 x 31 = 1581 нейронов. Размерность скрытого слоя ( слой 1 на рис.1) определяется количеством идеальных образцов, хранимых сетью, т.е. 10 нейронов. Размерность выходного слоя равна размерности скрытого слоя нейронной сети, т.е. так же 10 нейронов. На выходе получаем вектор y(y0...y9) . Номер j , для которого yj[2]> 0, соответствует номеру класса входного образца. 45. Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество — понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1. Лингвистическая переменная — в теории нечетких множеств, переменная, которая может принимать значения фраз из естественного или искусственного языка. Например, лингвистическая переменная «скорость» может иметь значения «высокая», «средняя», «очень низкая» и т. д. Фразы, значение которых принимает переменная, в свою очередь являются именами нечетких переменных и описываются нечетким множеством. Математическое определение лингвистической переменной Лингвистической переменной называется пятерка {x,T(x),X,G,M}, где x — имя переменной; T(x) — множество имен лингвистических значений переменной x, каждое из которых является нечеткой переменной на множестве X; G есть синтаксическое правило для образования имен значений x; M есть семантическое правило для ассоциирования каждой величины значения с ее понятием. Пример: Рассмотрим лингвистическую переменную, описывающую возраст человека, тогда: x: «возраст»; X: множество целых чисел из интервала [0, 120]; T(x): значения «молодой», «зрелый», «старый»; G: «очень», «не очень». Такие добавки позволяют образовывать новые значения: «очень молодой», «не очень старый» и пр. M: математическое правило, определяющее вид функции принадлежности для каждого значения из множества T. НЕЧЕТКИЙ ВЫВОД Вид вывода, часто встречающийся при моделировании рассуждений, опирающихся на человеческую практику. Конечно, в реальной жизни при обосновании своих утверждений люди вряд ли придерживаются законов математической логики. Они делают это иными способами. Вот пример такого вывода: Я часто хожу гулять вечером, если нет дождя. К сожалению, в последнее время дожди идут очень часто. В последнее время я редко выхожу вечером гулять. Два высказывания, написанные над чертой, отражают посылки, на которых основывается вывод, написанный под чертой. Три словосочетания важны в этом переводе: "часто", "очень часто" и "редко". Если отвлечься от содержательной части нашего примера, то вывод можно представить схемой: "Если Х часто, когда нет Y, и Y очень часто, то Х редко". Эта схема - пример нечеткого вывода. Вместо двух слов: "истина" и "ложь", используемых в традиционном выводе и отражающих значения переменной "истина", в нечетком выводе используются переменные, принимающие ряд значений. В нашем примере мы имели дело с переменной "частота". Приведем еще один пример, в котором используется переменная "расстояние". Дом стоит недалеко от озера. Озеро примыкает своей дальней стороной к лесу. Дом находится не очень далеко от леса. Используемая здесь схема имеет вид: "Если Х недалеко от У и У примыкает к Z, то Хне очень далеко от Z". Переменные, значениями которых являются некоторые словесные оценки, называются лингвистическими переменными. Именно они характерны для нечеткого вывода. Кроме того, нечеткий вывод является не достоверным, а лишь правдоподобным. Люди могут соглашаться или не соглашаться с его схемами. К тому же сами схемы могут оправдываться или не оправдываться в конкретных условиях. Например, последняя из приведенных нами схем может оказаться совершенно неприемлемой, если озеро, о котором идет речь, - это какое-то очень большое озеро (например, Байкал). Тогда, конечно, в выводе должно использоваться не "не очень далеко", а "очень далеко". Несмотря на сказанное, нечеткий вывод используется очень широко, ибо он отражает сумму человеческих знаний о многих явлениях реального мира. При планировании поведения в роботах и других системах искусственного интеллекта, действующих в не полностью описанных средах, при принятии решений в условиях отсутствия исчерпывающей информации, в экспертных системах при частичных знаниях о предметной области и во многих других ситуациях без нечеткого вывода не обойтись. |

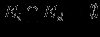 ,
,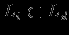 ,
,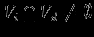 ,
,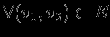 :
: 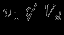 .
.