1. Классификация моделей представления знаний

Вид материала

Документы

Содержание 18. Основные модели представления знаний в экспертных системах. Фрейм (англ. frame – рамка, каркас) – 7. Синтаксис и семантика атомных формул. Семантика термов и формул. 12. Фреймы. Основные определения и понятия. Примеры.

Подобный материал:

• Экспертные системы и базы знаний, 42.45kb.
• Знаний. Модели представления знаний: логическая, сетевая, фреймовая, продукционная, 215.44kb.
• Системы искусственного интеллекта, 15.16kb.
• Техническое задание на выполнение курсовой работы на тему: Исследование моделей представления, 32.74kb.
• Судомоделирование, 131.6kb.
• План изучения дисциплины № п/п, 155.57kb.
• Лекции по дисциплине «Математическое моделирование» для студентов и магистрантов специальности, 21.92kb.
• 2. Лекция: Системы представления знаний, 171.88kb.
• Программа по курсу " Моделирование систем управления, 30.71kb.
• Программа курса «экономика труда», 585.26kb.

Примеры

Выражение



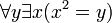
является предложением, т.к имеет фиксированную таблицу истинности. Для любого значения y можно определить истинность этого выражения, y - связанная переменная. Напротив, выражение



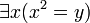
не является предложением, т.к. здесь y - свободная переменная. Для этого выражения нельзя построить таблицу истинности, т.к. на y не наложено никаких ограничений.


18. Основные модели представления знаний в экспертных системах.


Экспертная система (ЭС) – это специальный программный комплекс, аккумулирующий знания специалистов в конкретной предметной области и обеспечивающий пользователя возможностями [2]:

- решения широкого круга неформализуемых задач в различных предметных областях, которые до недавнего времени считались малодоступными для использования вычислительной техники;

- трансформирования опыта специалистов-экспертов в память компьютера путем создания и развития базы знаний;

- достижения более устойчивых результатов в решении задач за счет исключения эмоциональных и других факторов человеческой деятельности;

- получения значительных доходов за счет низкой стоимости эксплуатации системы и привлечения менее квалифицированных специалистов.

Под неформализуемыми задачами понимаются задачи, которые невозможно представить в числовой форме ввиду неточной определенности исходной информации, а также операций и целей ее преобразования. К таким задачам относятся задачи классификации, диагностики, проектирования, принятия решений в условиях неопределенности и др.

Основными отличительными характеристиками экспертных систем по отношению к прикладным и другим интеллектуальным программным системам являются:

• формирование даже в случае неточной исходной информации выводов и рекомендаций по решению задачи на основе базы знаний (БЗ) с возможностью объяснения полученных результатов;
  
• использование для решения задач в основном эвристических методов поиска, которые, в отличии от алгоритмических методов, не всегда гарантируют полноту решения задачи;
  
• моделирование механизма мышления специалистов (экспертов) в данной предметной области реального мира;
  
• достаточно высокая производительность, т. е. практически приемлемая скорость получения достоверного решения задачи.
  

Исторически первыми экспертными системами были Heuristic DENDRAL и Meta-DENDRAL, разработанные в середине 60-х годов XX века в Станфордском университете и предназначенные для расшифровки структуры соединений органической химии.

Информационной основой экспертной системы являются база данных и база знаний.

База данных содержит формализованную информацию об отдельных фактах, характеризующих объекты, процессы и явления предметной области, а также их свойства (например, данные о производственной продукции, технологическом оборудовании, физико-химических свойствах веществ и т.д.).

На данных, полученных практическим путем, основываются знания, представляющие собой структурированные данные (метаданные), характеристическими признаками которых являются:

• активность - возможность программной генерации новых знаний (в отличии от данных, которые пассивно хранятся в памяти компьютера);
  
• интегрируемость - существование возможности разъяснения смысла знаний;
  
• связность - описание закономерностей относительно фактов, явлений, процессов и причинно-следственных отношений между ними, позволяя специалистам ставить и решать практические задачи в данной предметной области;
  
• структурированность - возможность декомпозиции сложных объектов и установления связей между составляющими объектами с использованием отношения типа «часть - целое".
  

Естественен переход от данных к знаниям как следствие развития и усложнения информационно-логических структур, обрабатываемых вычислительной техникой.

База экспертных знаний (знаний специалистов в соответствующей предметной области) является главной составной частью экспертной системы.

В настоящее время основными классами моделей представления знаний в экспертных системах являются фреймы, семантические сети, продукционные модели и модели нечетких знаний [3, 4].

Фрейм (англ. frame – рамка, каркас) – познавательная структура, дающая целостное представление об объектах, явлениях и их типах в виде абстрактных образов для представления стереотипа восприятия.

Структура фрейма представляется в виде:


N : {1,V₁.P₁>,...,k,V_k,P_k>,...,n,V_n,P_n>},


где N - имя фрейма; k,V_k,P_k> (k=1,...,n) – слот; S_k – имя слота; V_k – значение слота; P_k– процедура.

Слоты – это структурные элементы фрейма, заполнение которых приводится к тому, что фрейм ставится в соответствие некоторой ситуации, явлению, объекту или процессу.

Имена фреймов и слотов обеспечивают интерпретируемость хранящихся во фреймах значений. Фреймы имеют свойство вложенности, т.к. значениями слота могут быть имена слотов более глубокого уровня. Значениями слотов могут быть приказы вызова процедур для активизации программ на основе имеющихся значений. Различают фреймы-образцы (прототипы), хранящиеся в БЗ, и фреймы-экземпляры, отображающие реальные ситуации на основе поступающих данных. Знания предметной области представляются фреймами-объектами, фреймами-сценариями, фреймами-ролями, фреймами-ситуациями и др. Например, фреймами-объектами можно представить знания о веществах, процессах и аппаратах, производственных технологических схемах и т.д.

Фреймы математически представляются как ориентированные графы с помеченными вершинами и дугами. Они отражают концептуальную основу организации памяти человека, обладают наглядностью, модульностью, объединяют достоинства процедурного и декларативного представления знаний, эффективны при обработке семантической составляющей знаний.


7. Синтаксис и семантика атомных формул.


Синтаксис формул. Формулами являются: p(t₁,...,t_k) – атомная формула, где p – предикатный символ, t₁,...,t_k (k  Nat) – термы (аргументы атомной формулы); p(t₁,...,t_k) – отрицательная атомная формула;t₁ @ t₂, где t₁ и t₂ – термы, «@»  {=, , >, <, , , , , , }; f₁ @ f₂ – логическое выражение, где «@»  {&, V}; (Z_n (v : t) f) - обобщенная формула, где Z_n  {&, V} – знак обобщенной операции, v – переменная (индекс операции), t – терм-множество, задающий область значений v, f – формула (тело обобщенной операции), содержащая индекс операции v.

Семантика термов и формул. Семантика термов и формул определяет значения термов и формул, а также условия, при которых эти значения существуют.

Будем предполагать, что на множестве имен задана функция , значение которой для каждого имени есть интерпретация этого имени. Значения термов и формул будут определены относительно функции интерпретации  и произвольной допустимой подстановки  значений вместо всех свободных переменных терма или формулы. Обозначим J_,(t)- значение терма t для функции интерпретации  и допустимой подстановки , J_,(f) значение формулы f для функции интерпретации  и допустимой подстановки , (v) - значение переменной v при подстановке .

Значения термов определяются следующим образом:

1. J_,(n) = (n), где n – имя; J_,(n) не зависит от ;

2. J_,(v) = (v), где v - переменная;

3. J_,(I), J_,(R)? J_,(S) – соответственно множество всех целых или вещественных чисел или бесконечное множество всех возможных имен, J_,(I) не зависит от  и ;

4. J_,() - пустое множество; J_,() не зависит от  и ;

5. J_,({t₁,t₂,...,t_k}) = {J_,(t₁), J_,(t₂), ..., J_,(t_k)}, т.е. значение этого терма есть множество, элементами которого являются J_,(t₁), J_,(t₂),..., J_, (t_k); терм имеет значение, если для функции интерпретации  и подстановки  имеют значения термы t₁, t₂,..., t_k;

6. J_,(I[t₁,t₂]) (J_,(R[t₁,t₂])) есть множество всех целых (вещественных) чисел, не меньших J_,(t₁) и не больших J_,(t₂); терм имеет значение, если J_,(t₁) и J_,(t₂) являются числами и имеет место J_,(t₁)J_,(t₂);

7. J_,(t₁ ¤ t₂) = J_,(t₁) ¤ J_,(t₂), где «¤»  {+, -, *, /}; терм имеет значение, если J_,(t₁) и J_,(t₂) являются числами;

8. J_,(t₁ ¤ t₂) = J_,(t₁) ¤ J_,(t₂), где «¤»  {, , \}; терм имеет значение, если J_,(t₁) и J_,(t₂) являются множествами;

9. J_,((t)) - мощность множества J_,(t); терм имеет значение, если J_,(t) является конечным множеством;

10. J_,(+ (v:t₁) t₂) = 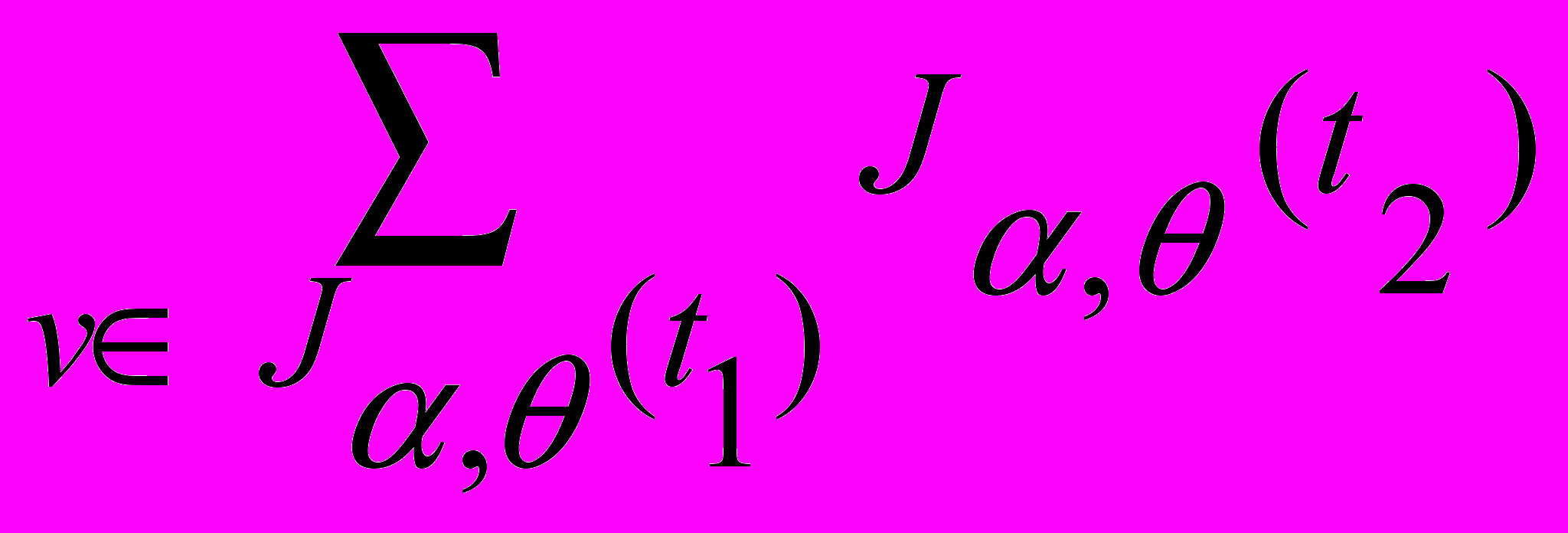, т.е. J_,(+(v:t₁) t₂) равно сумме значений J_,(t₂), при условии, что связанная переменная v пробегает все элементы множества J_,(t₁); терм имеет значение, если J_,(t₁) является множеством, а J_,(t₂) - числом при замене переменной v любым элементом множества J_,(t₁);

11. J_,(* (v:t₁) t₂) = 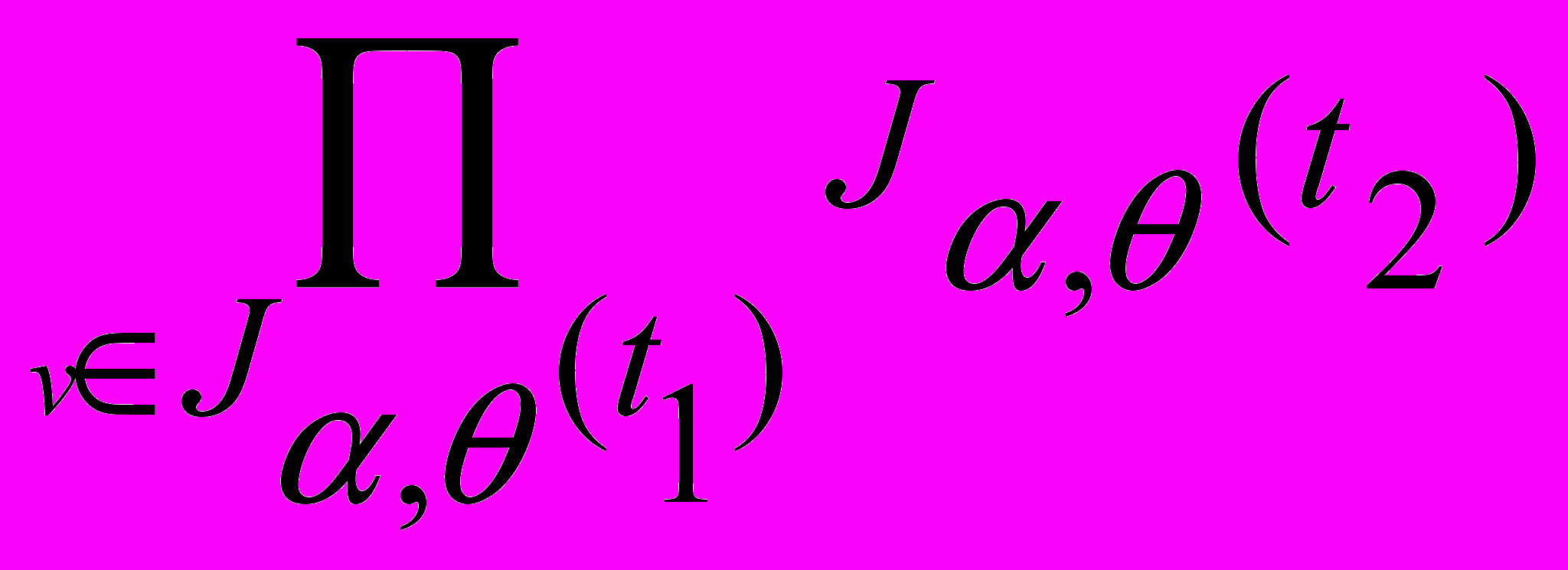, т.е. J_,(+ (v:t₁) t₂) равно произведению значений J_,(t₂), при условии, что связанная переменная v пробегает все элементы множества J_,(t₁); терм имеет значение, если J_,(t₁) является множеством, а J_,(t₂) - числом при замене переменной v любым элементом множества J_,(t₁);

12. J_,( (v:t₁) t₂) = 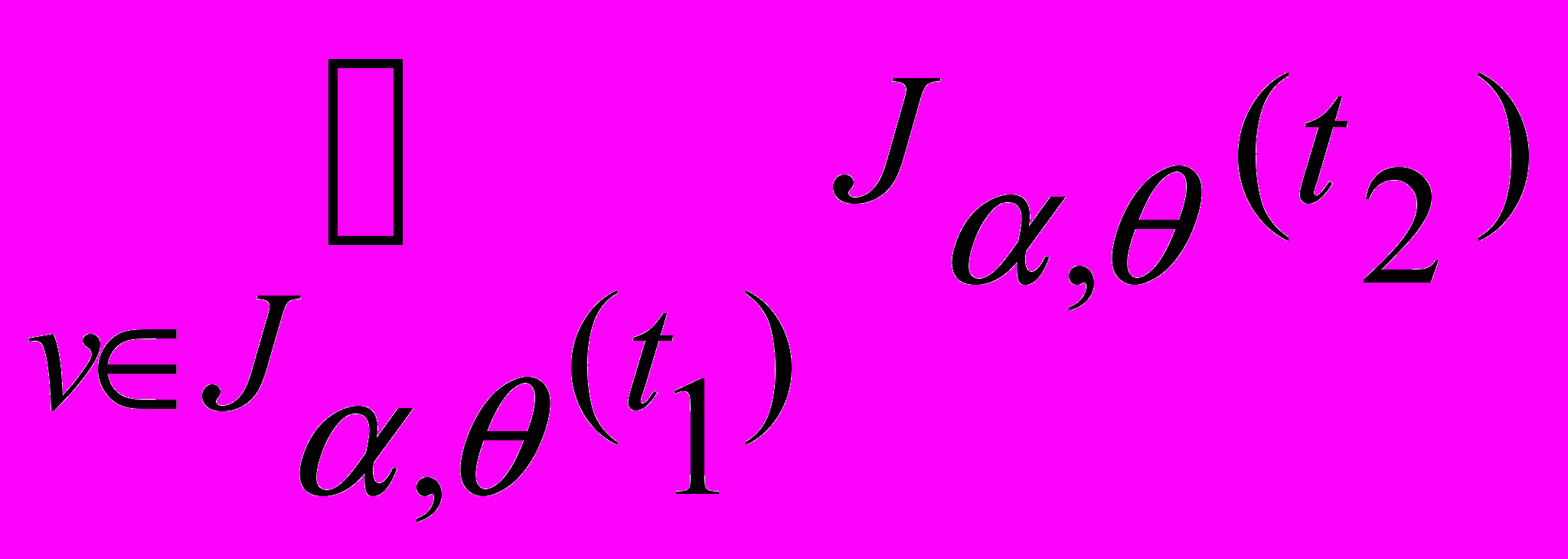, т.е. J_,( (v:t₁) t₂) равно объединению значений J_,(t₂), при условии, что связанная переменная v пробегает все элементы множества J_,(t₁); терм имеет значение, если J_,(t₁) является множеством, а J_,(t₂) - множеством при замене переменной v любым элементом множества J_,(t₁);

13. J_, (((v:t₁) t₂) = 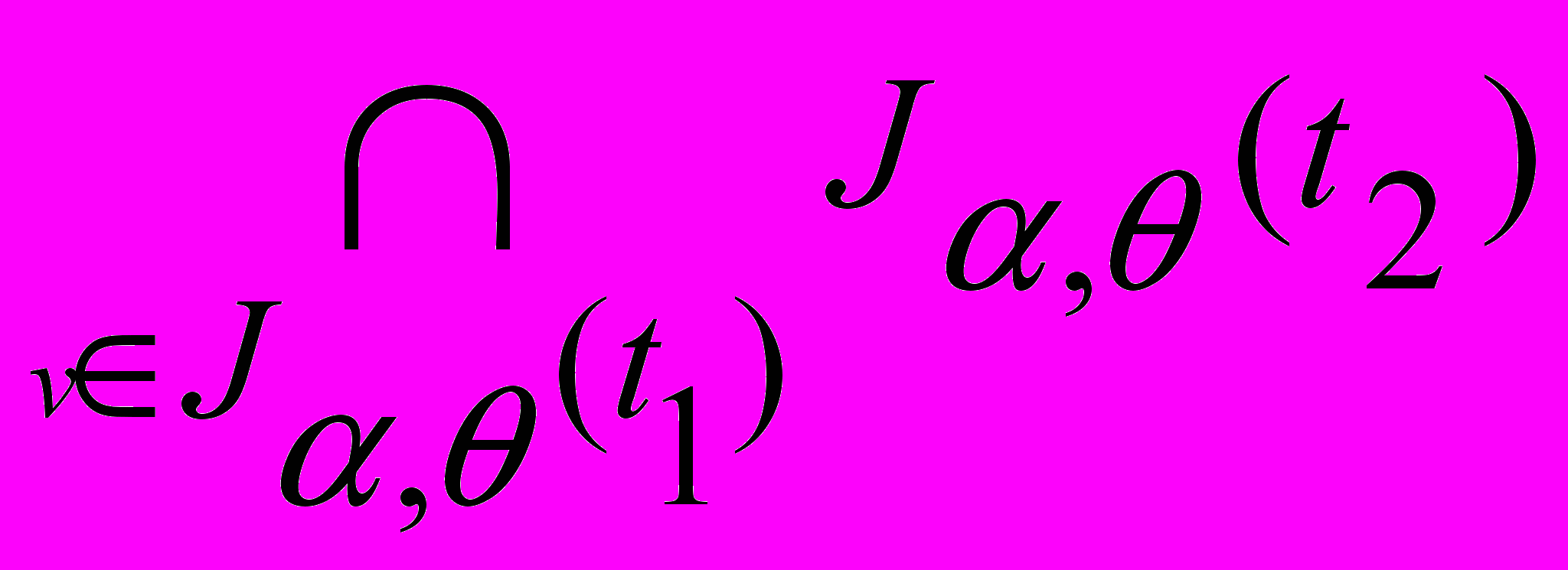т.е. J_, ( (v:t₁) t₂) равно пересечению значений J_,(t₂), при условии, что связанная переменная v пробегает все элементы множества J_,(t₁); терм имеет значение, если J_,(t₁) является множеством, а J_,(t₂) - множеством при замене переменной v любым элементом множества J_,(t₁).

13. J_,(jota (v:t) f) равно тому элементу множества J_,(t), при подстановке которого вместо переменной v значение J_,(f) есть истина; терм имеет значение, если значение J_,(t) является множеством, а его элемент, при подстановке которого вместо v значение J_,(f) есть истина, является единственным; 14. J_,(f(t₁,t₂,...,t_k)) = (J_,(t₁),J_,(t₂),...,J_,(t_k)) - значение функции , которая есть интерпретация имени J_,(f) (т.е.  = (J_,(f))), от аргументов J_,(t₁),...,J_,(t_k); заметим, что если t' - терм, такой, что J_,(t') = _,(t₁),J_,(t₂),...,J_,(t_k)>, то J_,(f(t'))=J_,(f(t₁,t₂,...,t_k));


12. Фреймы. Основные определения и понятия. Примеры.

Фрейм — (англ. frame — «каркас» или «рамка») — способ представления знаний в искусственном интеллекте, представляющий собой схему действий в реальной ситуации. Первоначально термин «фрейм» ввёл Марвин Минский в 70-е годы XX века для обозначения структуры знаний для восприятия пространственных сцен. Фрейм — это модель абстрактного образа, минимально возможное описание сущности какого-либо объекта, явления, события, ситуации, процесса.

Фреймы используются в системах искусственного интеллекта (например, в экспертных системах) как одна из распространенных форм представления знаний.