1. Классификация моделей представления знаний
| Вид материала | Документы |
- Экспертные системы и базы знаний, 42.45kb.
- Знаний. Модели представления знаний: логическая, сетевая, фреймовая, продукционная, 215.44kb.
- Системы искусственного интеллекта, 15.16kb.
- Техническое задание на выполнение курсовой работы на тему: Исследование моделей представления, 32.74kb.
- Судомоделирование, 131.6kb.
- План изучения дисциплины № п/п, 155.57kb.
- Лекции по дисциплине «Математическое моделирование» для студентов и магистрантов специальности, 21.92kb.
- 2. Лекция: Системы представления знаний, 171.88kb.
- Программа по курсу " Моделирование систем управления, 30.71kb.
- Программа курса «экономика труда», 585.26kb.
| 23. Определение лингвистической переменной. Лингвистическая переменная — в теории нечетких множеств, переменная, которая может принимать значения фраз из естественного или искусственного языка. Например, лингвистическая переменная «скорость» может иметь значения «высокая», «средняя», «очень низкая» и т. д. Фразы, значение которых принимает переменная, в свою очередь являются именами нечетких переменных и описываются нечетким множеством. Математическое определение лингвистической переменной Лингвистической переменной называется пятерка {x,T(x),X,G,M}, где x — имя переменной; T(x) — множество имен лингвистических значений переменной x, каждое из которых является нечеткой переменной на множестве X; G есть синтаксическое правило для образования имен значений x; M есть семантическое правило для ассоциирования каждой величины значения с ее понятием. Пример: Рассмотрим лингвистическую переменную, описывающую возраст человека, тогда: x: «возраст»; X: множество целых чисел из интервала [0, 120]; T(x): значения «молодой», «зрелый», «старый»; G: «очень», «не очень». Такие добавки позволяют образовывать новые значения: «очень молодой», «не очень старый» и пр. M: математическое правило, определяющее вид функции принадлежности для каждого значения из множества T. 20. Сетевые модели представления знаний. Сетевые модели Способ представления знаний в сетевых моделях наиболее близок к тому, как они представлены в текстах на естественном языке. В его основе лежит идея о том, что вся необ- ходимая информация может быть описана как совокупность троек (arb), где a и b - объекты, а r - бинарное отношение между ними. Формально сетевые модели могут быть заданы в виде H = <I, C1, ..., Cn, Г>, где I - множество информационных единиц, C1,..., Cn - множество типов связей между эле- ментами I, отображение Г задает между ИЕ, входящими в I, связи из заданного набора типов связей {Ci}. 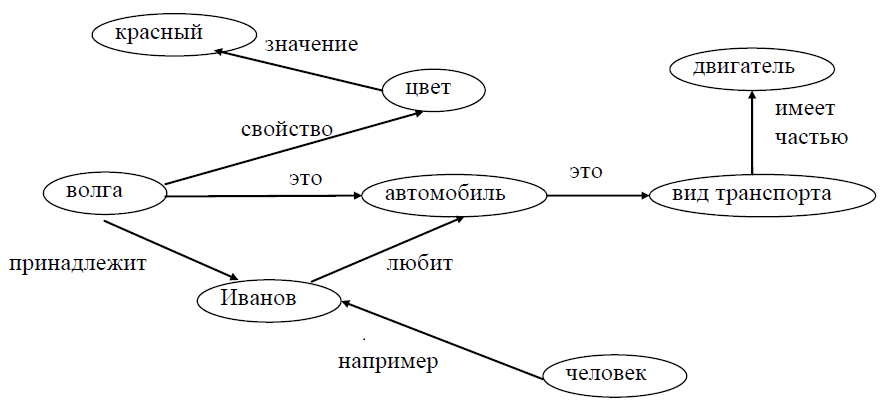 Если в сетевой модели допускаются связи различного типа, то ее называют семанти- ческой сетью (СС).
Нечёткое множество — понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1 Операции над нечёткими множествамиПри 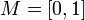 Пересечением нечётких множеств A и B называется наибольшее нечёткое подмножество, содержащееся одновременно в A и B: 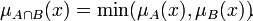 Произведением нечётких множеств A и B называется нечёткое подмножество с функцией принадлежности: 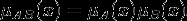 Объединением нечётких множеств A и B называется наименьшее нечёткое подмножество, содержащее одновременно A и B: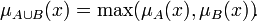 
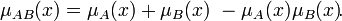
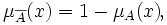 для каждого 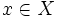 .15. Данные и знания. Основные отличия. Да́нные (калька от англ. data) — это представление фактов и идей в формализованном виде, пригодном для передачи и обработки в некотором информационном процессе. Изначально — данные величины, то есть величины, заданные заранее, вместе с условием задачи. Противоположность — переменные величины. В информатике Данные — это результат фиксации, отображения информации на каком-либо материальном носителе, то есть зарегистрированное на носителе представление сведений независимо от того, дошли ли эти сведения до какого-нибудь приёмника и интересуют ли они его [1]. Данные — это и текст книги или письма, и картина художника, и ДНК. Данные, являющиеся результатом фиксации некоторой информации, сами могут выступать как источник информации. Информация, извлекаемая из данных, может подвергаться обработке, и результаты обработки фиксируются в виде новых данных. Данные могут рассматриваться как записанные наблюдения, которые не используются, а пока хранятся. Информация, отображаемая данными, может быть непонятна приемнику (шифрованный текст, текст на неизвестном языке и пр.). Зна́ние — форма существования и систематизации результатов познавательной деятельности человека. Знание помогает людям рационально организовывать свою деятельность и решать различные проблемы, возникающие в её процессе. Зна́ние — в теории искусственного интеллекта и экспертных систем — совокупность информации и правил вывода (у индивидуума, общества или системы ИИ) о мире, свойствах объектов, закономерностях процессов и явлений, а также правилах использования их для принятия решений. Главное отличие знаний от данных состоит в их структурности и активности, появление в базе новых фактов или установление новых связей может стать источником изменений в принятии решений. 3на́ния фиксируются в образах и знаках естественных и искусственных языков. Знание противоположно незнанию (отсутствию проверенной информации о чём-либо). Главное отличие знаний от данных состоит в их структурности и активности, появление в базе новых фактов или установление новых связей может стать источником изменений в принятии решений. 51. Гибридные системы. Под гибридной интеллектуальной системой принято понимать систему, в которой для решения задачи используется более одного метода имитации интеллектуальной деятельности человека. Таким образом ГИС — это совокупность:
Междисциплинарное направление «гибридные интеллектуальные системы» объединяет ученых и специалистов, исследующих применимость не одного, а нескольких методов, как правило, из различных классов, к решению задач управления и проектирования. 13. Фреймы и их применение в экспертных системах. Фрейм — (англ. frame — «каркас» или «рамка») — способ представления знаний в искусственном интеллекте, представляющий собой схему действий в реальной ситуации. Первоначально термин «фрейм» ввёл Марвин Минский в 70-е годы XX века для обозначения структуры знаний для восприятия пространственных сцен. Фрейм — это модель абстрактного образа, минимально возможное описание сущности какого-либо объекта, явления, события, ситуации, процесса. Фреймы используются в системах искусственного интеллекта (например, в экспертных системах) как одна из распространенных форм представления знаний. Начиная с 1960-х годов, использовалось понятие фрейма знаний или просто фрейма. Каждый фрейм имеет своё собственное имя и набор атрибутов, или слотов которые содержат значения; например фрейм дом мог бы содержать слоты цвет, количество этажей и так далее. Использование фреймов в экспертных системах является примером объектно-ориентированного программирования с наследованием свойства, которое описывается связью «is-a» («является»). Однако в использовании связи «is-a» существовало немало противоречий: Рональд Брахман написал работу, озаглавленную «Чем является и не является IS-A», в которой были найдены 29 различных семантик связи «is-a» в проектах, чьи схемы представления знаний включали связь «is-a». Другие связи включают, например, «has-part» («имеет своей частью»). Фреймовые структуры хорошо подходят для представления знаний, представленных в виде схем и стереотипных когнитивных паттернов. Элементы подобных паттернов обладают разными весами, причем большие весы назначаются тем элементам, которые соответствуют текущей когнитивной схеме (schema). Паттерн активизируется при определённых условиях: если человек видит большую птицу, при условии что сейчас активна его «морская схема», а «земная схема» — нет, он классифицирует её скорее как морского орлана, а не сухопутного беркута. Фреймовые представления объектно-центрированы в том же смысле, что и семантическая сеть: все факты и свойства, связанные с одной концепцией, размещаются в одном месте, поэтому не требуется тратить ресурсы на поиск по базе данных. Скрипт — это тип фреймов, который описывает последовательность событий во времени; типичный пример — описание похода в ресторан. События здесь включают ожидание места, прочитать меню, сделать заказ, и так далее. Различные решения в зависимости от их семантической выразительности могут быть организованы в так называемый семантический спектр (англ. Semantic spectrum). 9. Система опровержений на основе резолюций. Резолюция - это правило вывода, используемое для построения опровержений (refutation). Важным практическим применением метода резолюции, в частности при создании систем опровержения, является современное поколение интерпретаторов языка PROLOG . Принцип резолюции (или разрешения), введенный в работе [Robinson, 1965], описывает способ обнаружения противоречий в базе данных дизъюнктивных выражений при минимальном использовании подстановок. Опровержение разрешения - это способ доказательства теоремы, основанный на формулировке обратного утверждения и добавлении отрицательного высказывания к множеству известных аксиом, которые по предположению считаются истинными. Затем правило резолюции используется для доказательства того, что такое предположение ведет к противоречию (доказательство от обратного). Поскольку в процессе доказательства теоремы показывается, что обратное утверждение несовместимо с существующим набором аксиом, исходное утверждение должно быть истинным. В этом и состоит доказательство теорем. Процесс доказательства от обратного состоит из следующих этапов.ь Предположения или аксиомы приводятся к дизъюнктивной форме (clause form) К набору аксиом добавляется отрицание доказываемого утверждения в дизъюнктивной форме. Выполняется совместное разрешение этих дизъюнктов, в результате чего получаются новые основанные на них дизъюнктивные выражения . Генерируется пустое выражение, означающее противоречие. Подстановки, использованные для получения пустого выражения, свидетельствуют о том, что отрицание отрицания - истинно. 5. Предикаты первого порядка. Основные определения и понятия. Предикатом называют предложение, принимающее только два значения: истина или ложь. Для обозначения предикатов применяются логические связки между высказываниями: ¬ не, или, и, если, а также квантор существования и квантор всеобщности. Допустимые выражения в исчислении предикатов называются правильно построенными формулами (ППФ), состоящими из атомных формул. Атомные формулы состоят из предикатов и термов, разделяемых круглыми, квадратными и фигурными скобками. Предикатные символы представляются в основном глагольной формой, например: ПИСАТЬ, УЧИТЬ, ПЕРЕДАТЬ, но не только глагольной формой, а формами существительных и прилагательных, например: КРАСНЫЙ, ЗНАЧЕНИЕ, ЖЕЛТЫЙ. Логика первого порядка (исчисление предикатов) — формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций и предикатов. Расширяет логику высказываний. В свою очередь является частным случаем логики высшего порядка. 4. Методы структурирования и формализации знаний. При формализации качественных знаний может быть использована теория нечетких множеств [Заде, 1974], особенно те ее аспекты, которые связаны с лингенетической неопределенностью, наиболее часто возникающей при работе с экспертами на естественном языке. Под лингвистической неопределенностью подразумевается не полиморфизм слов естественного языка, который может быть преодолен на уровне понимания смысла высказываний в рамках байесовской модели [Налимов, 1974], а качественные оценки естественного языка для длины, времени, интенсивности, для целей логического вывода, принятия решений, планирования. Лингвистическая неопределенность в системах представления знаний задается с помощью лингвистических моделей основанных на теории лингвистических переменных и теории приближенных рассуждении [Kikerf 1978]. Эти теории опираются на понятие нечеткого множества, систему операций над нечеткими множествами и методы построения функций принадлежности. Одним из основных понятий, используемых в лингвистических моделях, является понятие лингвистической переменной. Значениями лингвистических переменных являются не числа, а слова или предложения некоторого искусственного либо естественного языка. Например, числовая переменная "возраст" принимает дискретные значения между нулем и сотней, а целое число является значением переменной. Лингвистическая переменная "возраст" может принимать значения: молодой, старый, довольно старый, очень молодой и т. д. Эти термы-лингвистические значения переменной. На это множество (как и на числа) также налагаются ограничения. Множество допустимых значений лингвистической переменной называется терм-множеством. При вводе в ЭВМ информации о лингвистических переменных и терм-множестве ее необходимо представить в форме, пригодной для работы на ЭВМ. Лингвистическая переменная задается набором из пяти компонентов: <Л,Т(А), U, <7, Af>, где Л-имя лингвистической переменной; Г (Л)-ее терм-множество; U- область, на которой определены значения лингвистической переменной; 6 описывает операции по порождению производных значений лингвистической переменной на основе тех значений, которые входят в терм-множество. С помощью правил из О можно расширить число значений лингвистической переменной, т. е. расширить ее терм-множество. Каждому значению а лингвистической переменной Л соответствует нечеткое множествоХа, являющееся подмножеством V. По аналогии с формальными системами правила из G часто называют синтаксическими Наконец, компонент М образует набор семантических правил. С их помощью происходит отображение значений лингвистической переменной а в нечеткие множества Ха и выполняются обратные преобразования. Именно эти правила обеспечивают формализацию качественных утверждений экспертов при формировании проблемной области в памяти ИС. Одним из перспективных методов структурирования знаний является так называемый объектно ориентированный анализ. Общая методология ООА и основные принципы с точки зрения философии могут быть представлены как сплав всех трех направлений - Структурализма, Семиотики и Синергетики, с концентрированные на языке логико-математических абстракций. 29. Генетические алгоритмы. Генети́ческий алгори́тм (англ. genetic algorithm) — это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений. Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе. Применение генетических алгоритмовГенетические алгоритмы применяются для решения следующих задач:
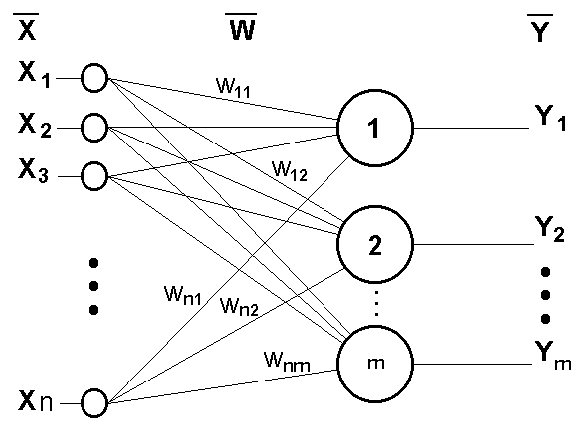
6. Модели представления знаний. Историческая справка. Модели представления знании делятся на детерминированные (жесткие) и мягкие. Детерминированные модели включают в себя фреймы, логико-алгебраические модели, семантические сети и продукционные модели. Мягкие модели включают в себя нечеткие системы, нейронные сети, эво-люционные модели, гибридные системы. Одним из основателей теории искусственного интеллекта считается известный английский ученый Алан Тьюринг, который в 1950 году опубликовал статью «Вычислительные машины и разум» . А. Ньюэлл, Дж. Шоу и Г. Саймон создали программу для игры в шахматы на основе метода, предложенного в 1950 году К. Шенноном, формализованного А. Тьюрингом и промоделированного им же вручную.В 1960 год была написана программа GPS универсальный решатель задач. Первые нейросети появились в конце 50-х годов.Первая международная конференция по искусственному интеллек-ту (IJCAI) состоялась в 1969 году в Вашингтоне. 1973 году был создан язык логического программирования Prolog. Первая экспертная система была создана Э. Фейгенбаумом в 1965 году. 33. Искусственные нейронные сети: алгоритмы обучения (алгоритм обучения по дельта правилу)
|
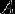называется множество 
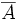с функцией принадлежности:
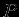- количество обработанных НС примеров;
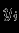- реальный выход НС;
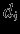- желаемый (идеальный) выход НС;
.
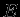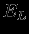(ошибка обучения) и по определенному алгоритму производится коррекция весов НС. Целью процедуры коррекции весов есть минимизация ошибки 
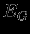(ошибка обобщения). Если результат неудовлетворительный то, производится модификация множества учебных примеров1 и повторение цикла обучения НС.