Утверждено Советом Факультета Председатель 200 Санкт-Петербург 2006 I. пояснительная записка

Вид материала

Пояснительная записка

Содержание Учебная задача курса Формы контроля Итоговая оценка Тема 1. Нормальный закон распределения. Тема 2. Распределения, связанные с нормальным распределением. Тема 3. Статистическое оценивание параметров распределения.. Тема 4. Статистическая проверка статистических гипотез. Тема 5. Обработка результатов наблюдения (обработка опытов Тема 7 Функция регрессии, линейная и множественная регрессия. Тема 8. Нелинейная регрессия и анализ временных рядов Распределение материала при проведении практических занятий Вопросы для подготовки к экзамену по эконометрике

Подобный материал:

• Утверждено Советом Факультета экономики Председатель декан Факультета экономики Слуцкий, 102.97kb.
• Утверждено Советом Факультета Председатель 200 г. Санкт Петербург 2010 содержание пояснительная, 206.17kb.
• Утверждено Советом Факультета Председатель 200 г Санкт Петербург 2010 содержание пояснительная, 191.69kb.
• Утверждено Советом Факультета Председатель 200 г. Санкт Петербург 2010 содержание пояснительная, 553.18kb.
• Утверждено Советом Факультета Председатель /А. В. Бутуханов/ 200 г. Санкт Петербург, 75.3kb.
• Утверждено Советом Факультета Председатель 200 г. Санкт Петербург 2010 содержание пояснительная, 453.72kb.
• Утверждено Советом Факультета Председатель 200 г. Санкт Петербург 2010 оглавление пояснительная, 105.7kb.
• Утверждено Советом Факультета Председатель 200 г. Санкт Петербург 2008 I. пояснительная, 194.73kb.
• Утверждено Советом Факультета экономики Председатель декан Факультета экономики Слуцкий, 221.51kb.
• Утверждено Советом Факультета Председатель 200 г. Санкт-Петербург 2010 Раздел пояснительная, 108.09kb.

Министерство экономического развития и торговли Российской Федерации


Государственный Университет –

Высшая школа экономики

Санкт-Петербургский филиал


Кафедра математики


Программа дисциплины

Эконометрика

Для факультета Менеджмента

Курс 3

Автор программы: к.т.н., доцент Рейнов Юрий Иванович

доцент Ванина Елена Андреевна


Согласовано УМО Одобрено на заседании кафедры

_______________ Зав. кафедрой______________

«9» июля 2005

«___»_________200


Утверждено Советом Факультета

_______________________

Председатель

_______________________

«___»______________200


Санкт-Петербург

2006


I. Пояснительная записка


Требования к студентам:

Учебная дисциплина «Эконометрика» (3, 4 модули 3-го курса факультета Менедж­мента) требует предварительных знаний по дисциплинам «Математический анализ», «Ли­нейная алгебра», «Вероятностно-статистические методы в менеджменте», «Анализ дан­ных в менеджменте»..

Аннотация:

Учебная дисциплина содержит основы математических знаний, базовые элементы экономико-математических моделей и методов, необходимые современному менеджеру. Программа дисциплины содержит разделы, посвященные таким вопросам, как анализ экономических показателей, анализ временных рядов, ряды Фурье и т.д. Учебная дисцип­лина направлена на привитие студентам - менеджерам целостного взгляда на математику, как основу для создания моделей управления на базе исследования поведения экономиче­ских характеристик. Работая в реальном мире, специалист - аналитик должен обязательно владеть именно математическим инструментарием - как пусть в определенной мере иде­альным, но зато инвариантным относительно разнообразных предметных областей сред­ством работы в них. Именно такое знание является одним из базовых элементов будущей профессиональной мобильности специалиста-управленца, необходимой для достижения им своего интегрального профессионального успеха в жизни.

Учебная задача курса:

В курсе «Эконометрика » сделан акцент на изучении общих правил (принципов), специальных приемов и методов статистического исследования, то есть положений, со­ставляющих теоретическую базу статистики.

Теоретический анализ явлений, основанных на социально-экономических принципах, всегда строится на его статистическом изучении. Освоение материалов курса является не­обходимым условием правильной организации статистического исследования и безоши­бочного толкования его результатов.

Излагаемый в курсе материал строится таким образом, чтобы наряду с умением оцени­вать характеристики отдельных статистических объектов (теория оценивания статистиче­ских параметров), студенты овладели методами изучения количественные изменения в явлениях, умели оценить существенность и несущественность наблюдаемых различий (теория гипотез), улавливали момент перехода количественных изменений в качествен­ные, выявляли зависимость изучаемого явления от окружающих условий (теория корре­ляции).

Сведения, содержащиеся в данном курсе, необходимы для изучения следующих дисци­плин

• Финансовый анализ
  
• Стратегическое планирование
  
• Финансовый менеджмент
  

Курс может быть использован для разработки и применения численных методов обра­ботки статистической информации, ее хранения и передачи данных.

Формы контроля:

По курсу предусмотрены две контрольные работы и одно домашнее задание, как текущий и промежуточный контроли. Ито­говым контролем работы студента является экзамен.

Все формы промежуточного, текущего и итогового контролей оцениваются в 10-балльной шкале. Итоговая оценка складывается:

• из оценки по первой контрольной работе - 10% итоговой оценки
  
• из оценки по второй контрольной работе - 10% итоговой оценки
  
• активности на семинарских занятиях в течение учебного года - 10% итоговой оценки
  
• из оценок по домашнему заданию — 30% итоговой оценки
  
• из оценки заключительного письменного экзамена - на 40% итоговой оценки.
  

Итоговая оценка (результат округления) выставляется в пятибалльной и в 10-балльной системах в ведомость и в зачетную книжку студента (оценкам 1, 2, 3 в 10-балльной систе­ме соответствует оценка «неудовлетворительно » в пятибалльной системе, оценкам 4, 5 — «удовлетворительно », оценкам 6, 7 — «хорошо », оценкам 8, 9, 10 - «отлично »).


II. Содержание программы

Тема 1. Нормальный закон распределения.

Лекция 1. Нормальные функции и нормальный закон распределения. Его параметры. Сложение независимых нормальных величин. Моменты нормального распределения. Вероятность попадания случайной величины, подчиненной нормальному закону, на за­данный интервал. Вероятное отклонение. Роль нормального распределения в статистике.

Тема 2. Распределения, связанные с нормальным распределением.

Лекция 2. Распределение средней арифметической для выборок из нормальной совокуп­ности. Распределение Стьюдента Распределение дисперсии в выборках из нормальной генеральной совокупности. Распределение х² - Пирсона Z - Распределение Фишера.

Тема 3. Статистическое оценивание параметров распределения..

Лекция 3 Постановка задачи оценивания параметров. Основные свойства оценок. Клас­сификация выборочных оценок для неизвестных параметров закона распределения. Осо­бенности обработки малых выборок и построение их оценок. Выборочные оценки для неизвестных параметров закона распределения.

Лекция 4. Оценки для математического ожидания и дисперсии. Точечное оценивание па­раметров. Метод моментов. Точечное оценивание параметров. Метод наибольшего прав-доподобия. Понятие доверительного интервала и доверительной вероятности. Прибли­женный метод построения доверительного интервала.

Лекция 5. Точные методы построения доверительных интервалов для параметров слу­чайной величины, распределенной по нормальному закону

построение доверительного интервала для математического ожидания при извест­ной дисперсии

построение доверительного интервала для математического ожидания при неиз­вестной дисперсии

построение доверительного интервала для дисперсии при известном и неизвест­ном математическом ожидании.

Тема 4. Статистическая проверка статистических гипотез.

Лекция б. Понятие статистической гипотезы. Общая постановка задачи проверки гипотез. Проверка гипотез о законе распределения. Критерий согласия х² ~ Пирсона Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона. Лекция 7. Оценивание двух дисперсий нормальных генеральных совокупностей. Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормаль­ной совокупности. Сравнение двух средних генеральных совокупностей, дисперсии кото­рых неизвестны и одинаковы (малые независимые выборки).

Тема 5. Обработка результатов наблюдения (обработка опытов).

Лекция 8. Сравнение оценок математического ожидания и дисперсии по случайной вы­борке с возвратом и без возврата. Вычисление объема выборки в случаях выборок с воз­вратом и без возврата. Оценка вероятности по частоте.

Лекция 9. Оценка вероятности по частоте. Метод наименьших квадратов. Сглаживание экспериментальных зависимостей по методу наименьших квадратов.

Тема 6. Регрессионная модель.

Лекция 10. Теоретическая и выборочная регрессия. Природа случайной составляющей. Линейность по переменным и параметрам. Оценивание параметров. Метод наименьших квадратов. Свойство оценок параметров.

Тема 7 Функция регрессии, линейная и множественная регрессия.

Лекция 11. Особенности регрессии, проходящей через начало координат. Методология экономического исследования на примере линейной регрессии для случая одной объяс­няющей переменной. Особенности представления результатов регрессионного анализа в пакетном режиме на ПЭВМ

Лекция 12. Множественная линейная регрессия. Проверка значимости коэффициентов для множественной линейной регрессионной модели. Матричная запись экономической мо­дели и оценок МНК.

Тема 8. Нелинейная регрессия и анализ временных рядов

Лекция 13. Функциональные преобразования переменных в линейной регрессионной мо­дели. Модели с постоянной эластичностью. Полиномиальная регрессия. Разложение сум­мы квадратов отклонений. Дисперсионный анализ.

Лекция 14. Анализ временных рядов и функции сравнения. Модели с динамическими пе­ременными. Ряды Фурье.

Распределение материала при проведении практических занятий

Практика 1. Закон распределения дискретной св. (текстовая форма задания задач) На­чальные и центральные моменты (с условием абсолютной сходимости). Практика 2. Нормальное распределение (вероятность попадания в интервал по заданным параметрам распределения, вероятность отклонения от среднего, плотность и функция распределения суммы св., границы св. по параметрам и т.д.)

Практика 2. Точечные оценки параметров. Метод моментов (рассматриваются задачи для дискретных и непрерывных случайных величин, с одним и двумя параметрами) Практика 3. Метод максимального правдоподобия (метод Фишера) для случая дискрет­ных случайной величины (один и два параметра).

Практика 4. Метод максимального правдоподобия для непрерывной случайной величи­ны (один и два параметра).

Практика 5. Интервальные оценки для математического ожидания при неизвестной дис­персии (приближенный метод) Интервальные оценки для математического ожидания для математического ожидания при известной дисперсии

Практика 6. Интервальные оценки для математического ожидания для математического ожидания при неизвестных дисперсии (t -распределение)

Практика 7. Интервальные оценки для дисперсии (%² - распределение и q — распре­деление).

Практика 8. Контрольная работа по материалам практики 1-8

Практика 9. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.

Практика 10. Оценивание двух дисперсий нормальных генеральных совокупностей Практика 11. Сравнение исправленной выборочной дисперсии с гипотетической гене­ральной дисперсией нормальной совокупности.

Практика 12. Сравнение двух средних генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)

Практика 13. Сравнение оценок математического ожидания и дисперсии по случайной выборке с возвратом и без возврата.

Практика 14. Вычисление объема выборки в случаях выборок с возвратом и без возврата. Оценка вероятности по частоте.

Практика 15. Оценка вероятности по частоте. Метод наименьших квадратов. Сглажива­ние экспериментальных зависимостей по методу наименьших квадратов.

Практика 16. Контрольная работа по материалам практики 10-16


III.Тематика


Примерный вариант контрольных и домашней работ:

1. Система (X,Y) задана табличным законом 2. Найти регрессионную зависимость по данным:
   

X -1 0 1 2 Найти функцию Х : 3 5 4 9 7 Проверить гипотезы,

Y 0 0.1 0.2 0.15 0.05 регрессии У : 1 2 3 4 5 и сделать

1 0.25 0.1 0.05 0.1 M (Yx ) = f (x ). прогноз для х_р = 15


3. Даны законы распределения Х - 1 2 4 У 0 1 5 Найти D(2X – 3Y + 2)

Р 0.3 0.1 0.6 Р 0.2 0.5 0.3

4. Построить линейное уравнение, провести F-тест, оценить статистическую значимость и найти доверительные интервалы параметров уравнения и коэффициента корреляции
   

Y : 9.3, 8.4, 7.1, 6.9, 5.2, 3.7

Х : 4.2, 5,1, 4. 0, 3.6, 3.1, 2.8

4. Даны следующие значения: 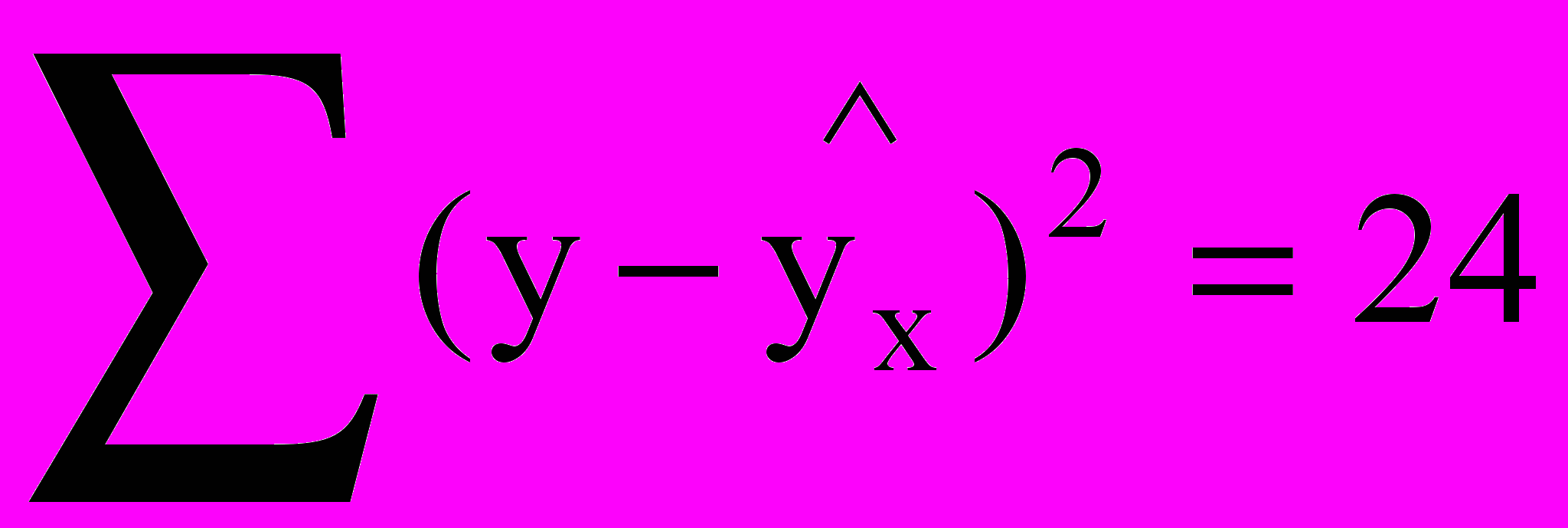, , 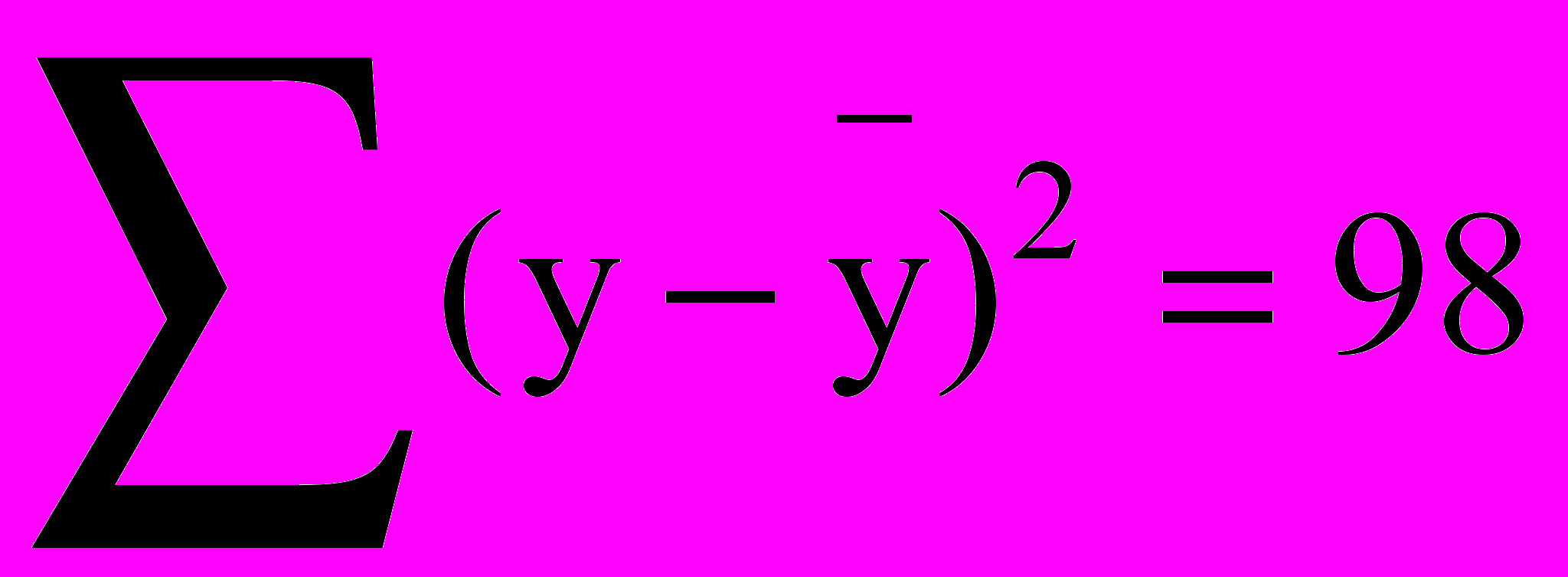n = 26.
   

Оценить качество уравнения и найти стандартную ошибку b


6.Дано уравнение y= 34 + 0.54 x, r² = 0.73, n = 16 m(b) = 0.32, m(a) = 21.2, m( r) =0.31

Необходимо:

• оценить статистическую значимость параметров регрессии и корреляции
  
• построить доверительные интервалы для всех параметров
  
• оценить точность прогноза
  

7. По регрессионной модели Y = + X +  изучалась зависимость прибыли Y от затрат на рекламу X. Данные по 20 предприятиям дали следующие результаты:  Y² =518,  X² =662, XY=486, Y=64, X=94. Оценить парметры , . Найти коэффициент детерминации и проверить гипотезу H_o :  .= 0 при 95 % и 99% критических значениях t – cтатистики.
   
8. Собраны данные по спросу и ценам на товары. Спрос ( y ) 7 6 5 4 3
   

Цена ( х ) 2 3 4 6 9

Расчитайте параметры уравнений линейной и показательной регрессии. Оцените качество каждой из моделей ( ошибку аппроксимации, коэффициент детерминации и F – тест ) и определите коэффициенты эластичности. Сделайте выводы по результатам.

9. При оценке парной регрессионной модели по 20 наблюдениям были получены следующие результаты

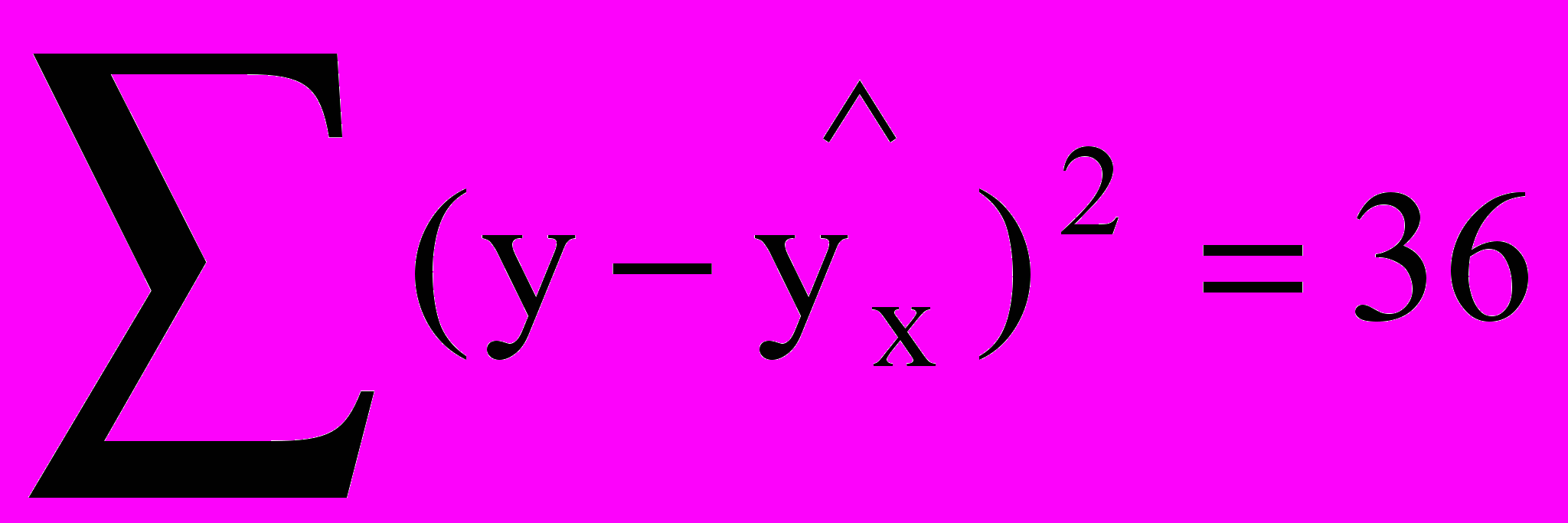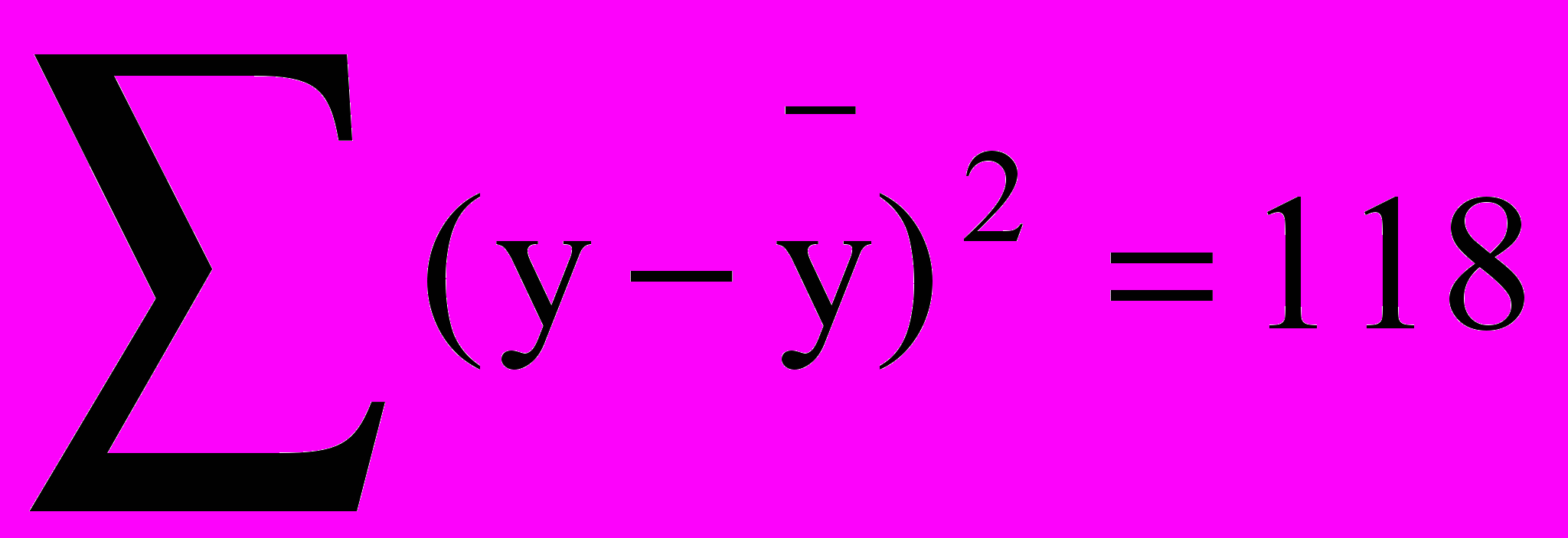, . Оцените качество уравнения и статистическую значимость коэффициента при независимой переменной ( уровень 0.05 ).

10. Собраны данные о доходах Х и потребительских расходах Y : ( в тыс. руб. )
    

Y 1 2 2 3 3

X 1 2 3 4 5 Используя линейную регрессию оцените статистическую значимость параметров (H_o : =.= r = 0 при 95 % ), рассчитайте доверительные интервалы для  и . Спрогнозируйте расходы при прогнозном значении дохода, составляющего 112 % от среднего дохода

10. Зависимость спроса Y на товар от цены Х для двух фирм характеризовалась по 10 наблюдениям логарифмическими регрессиями
    

Ln Y = 2.1 – 0.21Ln X (1) и Ln Y = -1.2 + 0.13Ln X (2)

Оцените эластичность спроса от цены и значимость уравнений через F – тест, если доля остаточной дисперсии в общей для (1) составляет 14%, а для (2) 8 %. Сделайте выводы.

12. Изучалась зависимость себестоимости от объемов. При оценке 30 наблюдений был получен промежуточный результат

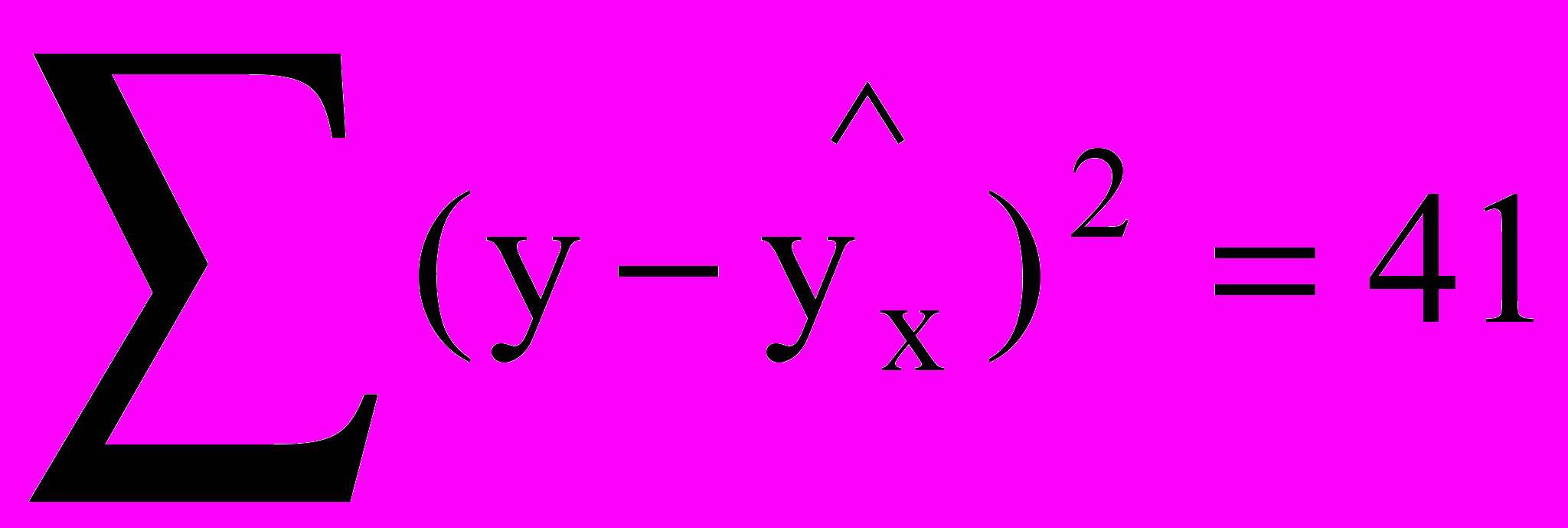. Проверьте устойчивость зависимости себестоимости от объемов, если известно, что значение факторной дисперсии в два раза превышает остаточную (при значимости 0.05). (гипотеза о случайности различий факторной и остаточной дисперсии)


ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО ЭКОНОМЕТРИКЕ

1. 
   Статистика (типы данных)
   

Модель (спецификация по переменным, спецификация по функциям)

Идея постановки задачи

2. Мера отклонения модели от начальных данных (четыре примера введения меры)
   
3. Первая ступень ограничений: линейность модели. Задача минимизации функционала, Необходимые условия
   
4. Первая ступень ограничений: линейность модели. Задача минимизации функционала. Достаточные условия (геометрический метод решения)
   
5. Теоретические и выборочные характеристики случайных величин. Аналоги в эконометрике. Свойства
   
6. Линейная одномерная регрессия. Постановка и решение задачи. Исследование единственности. Экономический смысл коэффициента регрессии.
   
7. Матричная форма системы нормальных уравнений и ее решение
   
8. Свойства системы нормальных уравнений
   
9. Коэффициент детерминации
   
10. Исследование зависимости коэффициентов регрессии от значений «Y». Свойства Zi.
    
11. Вторая ступень ограничений: условие Гаусса-Маркова. Геометрическая иллюстрация
    
12. Числовые характеристики случайных величин a, b – коэффициентов регрессии
    
13. Понятие случайной оценки неслучайного параметра. Теорема Гаусса-Маркова (док-во для коэффициента “b”).
    
14. Оценка S² дисперсии G² стохастической составляющей U_i. Оценка дисперсий случайных величин “a” и “b”
    
15. Третья ступень ограничений: предположение о нормальном распределении стохастической составляющей.
    
16. Построение случайных оценок a, b неслучайных параметров с использованием вероятностной меры (метод максимального правдоподобия).
    
17. Следствия из нормального распределения стохастической составляющей. Нормальное распределение и его свойства.
    
18. Основные статистические распределения. Прогнозирование в одномерной регрессии.
    
19. Построение доверительного интервала. План, пример построения доверительного интервала с использованием двухстороннего критерия Стьюдента
    
20. Многомерная регрессия: выборка, модель, гипотеза. Первая ступень ограничений
    
21. Выбор меры. Построение системы нормальных уравнений (в общем виде)
    
22. Пример построения и решения системы нормальных уравнений для модели с тремя регрессорами
    
23. Скорректированный коэффициент детерминации
    
24. Система нормальных уравнений для центрированной и нормальной выборки. Корреляционная матрица
    
25. Фиктивные переменные. Примеры использования
    
26. Вторая ступень ограничений: условие Гаусса-Маркова. Теорема Гаусса-Маркова
    
27. Третья ступень ограничений: предположение о нормальном распределении стохастической составляющей. Некоторые следствия.
    
28. Прогнозирование в многомерной регрессии
    
29. Многомерная регрессионная модель. Система нормальных уравнений в скалярной форме. Решение с помощью формул Крамера.
    
30. Запись и решение системы нормальных уравнений в центрированных и нормированных величинах. Связь полученных решений с ненормированными.
    
31. Коэффициент множественной детерминации. Частные коэффициенты корреляции.
    
32. Запись и решение системы нормальных уравнений в матричной форме.
    
33. Условия Гаусса-Маркова. Теорема Гаусса-Маркова. Оценка дисперсии случайной составляющей. Оценки дисперсии параметров.
    
34. Предположение о нормальном распределении случайной составляющей F-тест.
    
35. Предположение о нормальном распределении случайной составляющей t-тест.
    
36. Регрессия с линейными ограничениями.
    
37. Проблема объединения выборок.
    
38. Фиктивные переменные.
    
39. Прогнозирование в многомерных моделях.
    
40. Наличие линейной зависимости векторов в матрице наблюдений. Проблема мультиколлинеарности.
    
41. Нарушение условий Гаусса-Маркова: гетероскедостичность. Взвешенный метод наименьших квадратов.
    
42. Гетероскедостичность. Построение оценки дисперсии стохастической составляющей для двух частных случаев. Тест Голдфелда-Куанда.
    
43. Нарушение условий Гаусса-Маркова: авторегрессионный процесс первого порядка. Оценка параметра автокорреляции: процедура Кохрейна Орхатта.
    
44. Тест Дарбина-Уотсона на существование авторегрессии.
    
45. Историческая справка
    

IV.Учебно – методическое обеспечение программы

Базовый учебник.

Магнус В.П, Катушев П.К. Эконометрика. М., 2003 г.


Дополнительная литература:

1. Арский В.А. Математическая статистика. М, Высшая школа 1983
   
2. Долинин П.В., Игнатьева Е.С. Введение в статистические исследования. Минск,
   1978.
   
3. Гмурман В.Е. Теория вероятностей и математическая статистика. М. Высшая школа
   1977
   
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., Высшая школа, 1970
   
5. Гурский Е.И., Скобля Т.В., Юшкевич В.Э. Методическое пособие по теории вероятностей и математической статистике. Минск» 1973
   
6. Ивашев-Мусатов О. С. Теория вероятностей и математическая статистика М., Наука,
   1979
   
7. Карасев А.И. Теория вероятностей и математическая статистика М., Статистика,
   1979
   
8. Колемаев В.А., Староверов О.В., Турандаевский В.Б. Теория вероятностей и математическая статистика. М., Высшая школа, 1991
   
9. Лихолетов И.И., Мацкевич И.П. Руководство к решению задач по математической
   статистике и теории вероятностей. Минск, Высшая школа, 1966
   
10. Маркович Э.С. Курс высшей математики с элементами теории вероятностей. М.,
    Высшая школа, 1962
    
11. Микулик Н.А., Рейзина Г.Н. Решение экономических задач по теории вероятностей
    и математической статистике. М., Высшая школа, 1984
    
12. Румшинский Л.З. Элементы теории вероятностей. М.,Наука, 1988
    
13. Сборник задач по теории вероятностей, математической статистике и теории слу­
    чайных функций. Под редакцией А.А. Свешникова. М. Наука 1970
    

Кристофер Даугерти. Введение в эконометрику. М. 1997.


V. Тематический расчет часов

Название темы	Самостоятельная работа	Лекции	Семинары
Тема 1. Нормальный закон распределения.	7	2	2
Тема 2. Распределения, связанные с нормальным распределением.	7	2	2
Тема 3. Статистическое оценивание параметров распределения..	7	2	2
Тема 4. Статистическая проверка статистических гипотез.	7	2	2
Тема 5. Обработка результатов наблюдения (обработка опытов).	6	2	2
Тема 6. Регрессионная модель.	8	3	3
Тема 7 Функция регрессии. Линейная регрессия. МНК Множественная регрессия	7 7 7	3 3 3	3 3 3
Тема 8 Нелинейная регрессия. Анализ временных рядов	8 8	3 3	3 3
ИТОГО:	79	28	28