Учебная программа дисциплины специальные функции © бгу (Электронный документ)
| Вид материала | Программа дисциплины |
- Учебная программа дисциплины схемотехника © бгу (Электронный документ), 110.02kb.
- Учебная программа дисциплины языки описания радиоэлектронной аппаратуры © бгу (Электронный, 107.69kb.
- Рабочая учебная программа по дисциплине «Теория перевода» для специальности «031202, 514.42kb.
- Рабочая учебная программа по дисциплине «Практический курс перевода» для специальности, 682.26kb.
- Учебная программа для специальности: 1-24 01 02 Правоведение, 477.37kb.
- Базовая учебная программа дисциплины элементы вейвлет анализа для студентов специальностей, 124.17kb.
- Базовая учебная программа дисциплины «Математические основы wavelet -анализа» Для студентов, 84.83kb.
- Учебная программа «Специальные дисциплины» дополнительной профессиональной образовательной, 1942.52kb.
- Учебная программа дисциплины экономико-математические модели, 115.76kb.
- Базовая учебная программа дисциплины «алгебра и теория чисел» для студентов специальности, 183.29kb.
РД БГУ УПрД - 0001 – 2001
 | РУКОВОДЯЩИЙ ДОКУМЕНТ Белорусского государственного университета ___________________________________________ | |
| Одобрена Научно-методическим советом Белорусского государственного университета Протокол № от “___” _________ 200 г. | УТВЕРЖДАЮ Ректор Белгосуниверситета профессор Стражев В.И. “______” ____________________ 200 г. |
УЧЕБНАЯ ПРОГРАММА ДИСЦИПЛИНЫ
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
© БГУ (Электронный документ)
Минск
Предисловие
1 РАЗРАБОТАНА Белорусским государственным университетом
ИСПОЛНИТЕЛИ:
Мартыненко М. Д. - доктор физико-математических наук, профессор кафедры теоретической и прикладной механики механико-математического факультета БГУ.
ВНЕСЕНА Кафедрой теоретической и прикладной механики механико-математического факультета БГУ на основе образовательного стандарта специальности «Механика».
ОДОБРЕНА Научно-методическим советом Белорусского государственного университета (Протокол от № )
2 УТВЕРЖДЕНА И ВВЕДЕНА В ДЕЙСТВИЕ приказом Ректора Белорусского государственного университета от №
3 ВВЕДЕНА ВПЕРВЫЕ
© БГУ (Электронный документ)
Настоящий руководящий документ (учебная программа дисциплины) не может быть тиражирован и распространен без разрешения Белорусского государственного университета
_____________________________________________________________________________
Издан на русском языке
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Специальные функции в механике деформируемого твердого тела возникают как решения обыкновенных дифференциальных уравнений в различных криволинейных координатах. Это обуславливает необходимость изучения дифференциальных уравнений особой структуры, особенностью которых является вырождение порядка уравнения в граничных точках промежутка интегрирования. Наряду с этим ряд специальных функций может быть введен с помощью производящих функций. Поэтому специальный курс строится на основе этих двух подходов. Вначале изучаются особенности решений указанного класса дифференциальных уравнений и выводятся особенности постановки граничных задач для этих решений, доказываются теоремы типа Стеклова, обосновывающие разложение искомых решений в ограниченных и неограниченных пространственных областях.
Данная учебная программа предназначена для студентов высших учебных заведений, основная специальность которых связана с математикой и механикой.
«СПЕЦИАЛЬНЫЕ ФУНКЦИИ»
Цель курса «Специальные функции» заключается в формировании у студентов целостного представления о методах использования специальных функций для решения задач теории упругости, термоупругости, теории колебаний механических систем с распределенными параметрами и т. д.
Тематический план курса "Теория оболочек"
-
№ темы
Количество часов
Содержание курса
Лекции
Семинарские и практические
Тема I. Уравнения специальных функций
2
Тема II. Общие свойства решений специальных функций
2
1
Тема III. Постановка задач для уравнений специальных функций
2
1
Тема IV. Уравнения Бесселя. Представление функций Бесселя в виде ряда
2
1
Тема V. Рекуррентные соотношения для функций Бесселя
2
1
Тема VI. Интегральные представления функций Бесселя
2
Тема VII. Асимптотическое поведение функций Бесселя
2
1
Тема VIII. Задача Штурма – Луивилля для уравнений Бесселя
2
Тема IX. Полиномы Лежандра.
2
1
Тема X. Формула Родрига. Интегральные представления полиномов Лежандра
2
1
Тема XI. Присоединенные функции Лежандра. Сферические функции
2
Тема XII. Ортогональные полиномы. Полиномы Чебышева
2
1
Тема XIII. Полиномы Чебышева Эрмита
1
Тема XIV. Полиномы Чебышева – Лагерра
1
Всего аудиторных часов
28
10
ИТОГО:
38
Тема 1. Уравнения специальных функций
Различные способы определения специальных функций. Представление через производящую функцию. Представление через решение дифференциальных уравнений.
Тема 2. Общие свойства решений специальных функций
Функции Бесселя полуцелого аргумента. Ограниченные решения уравнений Бесселя.
Тема 3. Постановка задач для уравнений специальных функций
Задача Штурма – Луивилля для уравнения Лапласа в цилиндрических координатах.
Тема 4. Уравнения Бесселя.
Представление функций Бесселя в виде ряда
Функции Бесселя целого аргумента. Функции Бесселя мнимого аргумента. Формула Вебера.
Тема 5. Рекуррентные соотношения для функций Бесселя
Различные типы цилиндрических функций Бесселя. Функции Макдональда. Функции Кельвина.
Тема 6. Интегральные представления функций Бесселя
Интегралы, содержащие функции Бесселя.
Тема 7.. Асимптотическое поведение функций Бесселя
Асимптотика функций Бесселя на полубесконечном интервале.
Тема 8. Задача Штурма – Луивилля для уравнений Бесселя
Теорема Стеклова. Ортогональность и норма функций Бесселя.
Тема 9. Полиномы Лежандра.
Производящие функции для полиномов Лежандра. Рекуррентные соотношения.
Тема 10. Формула Родрига.
Интегральные представления полиномов Лежандра
Рекуррентные соотношения для полиномов Лежандра. Ортогональность и норма полиномов Лежандра.
Тема 11. Присоединенные функции Лежандра.
Сферические функции
Уравнение Лапласа в сферических координатах. Задача Штурма – Луивилля для сферы. Ортогональность и норма производящих функций.
Тема 12. Ортогональные полиномы.
Полиномы Чебышева
Полиномы, наименее уклоняющиеся от нуля. Полиномы
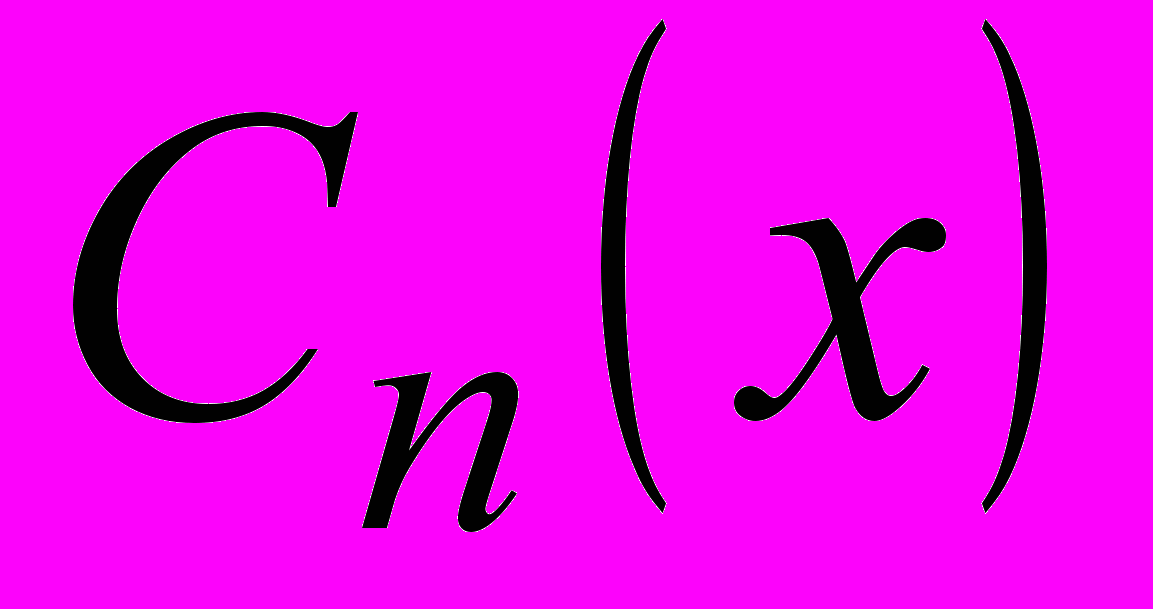 и
и 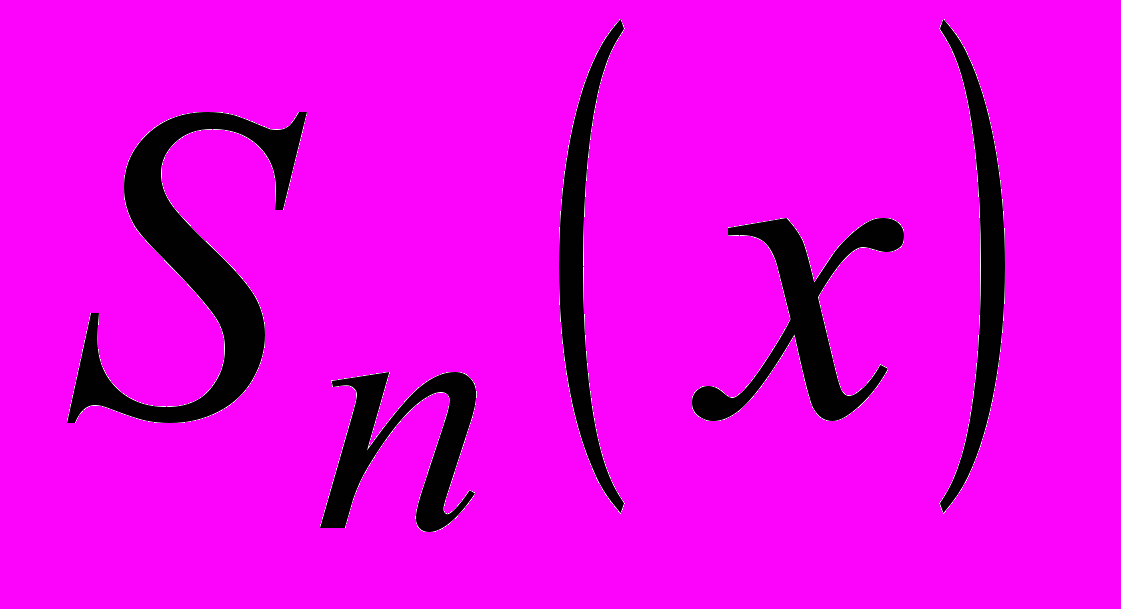 .
.Тема 13. Полиномы Чебышева Эрмита
Производящая функция полиномов Чебышева – Эрмита. Рекуррентные соотношения. Дифференциальные уравнения полиномов Чебышева – Эрмита.
Тема 14. Полиномы Чебышева – Лагерра
Производящая функция полиномов Чебышева – Лагерра. Рекуррентные соотношения. Дифференциальные уравнения полиномов Чебышева – Лагерра.
ЛИТЕРАТУРА
Ватсон Г. Н. Теория бесселевых функций. М.: ИЛ. 1949.
Грей Э.. Мэтьюз Г. Б. Функция Бесселя и их приложения к физике и механике. М.: ИЛ. 1953.
Джексон Д. Ряды Фурье и ортогональные полиномы. М.: ИЛ. 1948.
Лебедев Н. Н. Специальные функции и их приложения. М.: Физматгиз. 1963.
Тихонов А. Н., Самарский А. А. Уравнения математической физики. М.: Гостехиздат. 1953.
Уиттекер Э. Т., Ватсон Дж. Н. Курс современного анализа. Т. I – II. М.: Физматгиз. 1963.
Заведующий кафедрой
теоретической и прикладной механики
профессор М. А. Журавков
Согласована:
Начальник Главного управления
учебной и научно-методической работы
Белорусского государственного университета Е. Ф. Бондаренко
