Базовая учебная программа дисциплины «алгебра и теория чисел» для студентов специальности 1-31 03 01 «математика» Минск

Вид материала

Программа дисциплины

Содержание Курсов В.В. Гаращук М.С. Пояснительная записка «алгебра и теория чисел» Тематический план курса «Алгебра и теория чисел» Содержание курса Всего аудиторных часов Тема 2. Алгебраическая операция, основные алгебраические структуры. Тема 3. Поле комплексных чисел. Тема 4. Матрицы и операции над ними. Тема 5. Перестановки и подстановки. Тема 6. Определители и их применение. Тема 7. Многочлены от одной переменной. Тема 8. Сравнения и кольца вычетов. Раздел ii. векторные пространства, линейные отображения Тема 10. Системы линейных уравнений. Тема 11. Линейные отображения векторных пространств. Тема12. Инвариантные подпространства. Собственные векторы и собственные значения. Тема 13. Жорданова нормальная форма. Тема 14. Многочлены от нескольких переменных. ... Полное содержание

Подобный материал:

• Базовая учебная программа дисциплины «основы математической кибернетики» для студентов, 80.1kb.
• Базовая учебная программа дисциплины «введение в математику» для студентов специальности, 72.7kb.
• Базовая учебная программа дисциплины «Основания геометрии» для студентов специальности, 51.22kb.
• Примерная программа наименование дисциплины Алгебра и теория чисел Рекомендуется для, 486.84kb.
• Базовая учебная программа дисциплины «системы управления базами данных» для студентов, 80.99kb.
• Программы кандидатского экзамена по специальности 01. 01. 06 "Математическая логика,, 50.44kb.
• Базовая учебная программа дисциплины «методика преподавания математики» для студентов, 108.53kb.
• Базовая учебная программа дисциплины элементы вейвлет анализа для студентов специальностей, 124.17kb.
• Базовая учебная программа дисциплины «Математические основы wavelet -анализа» Для студентов, 84.83kb.
• Базовая учебная программа дисциплины «Основные направления современной философии» для, 714.19kb.

Министерство образования Республики Беларусь

Белорусский государственный университет

Механико-математический факультет

Кафедра высшей алгебры


УТВЕРЖДАЮ

Проректор по учебной работе

________________________

Рег.№ __________________

«____» ______________ 2007 г.


Базовая учебная программа дисциплины

«АЛГЕБРА И ТЕОРИЯ ЧИСЕЛ»

для студентов специальности 1-31 03 01 «математика »


Минск

2007


Авторы:


Тавгень О.И. – доктор физико-математических наук, заведующий кафедрой высшей алгебры ММФ, БГУ


Мельников О.В. – доктор физико-математических наук, профессор кафедры высшей алгебры ММФ, БГУ


Беняш-Кривец В.В. — доктор физико-математических наук, профессор кафедры высшей алгебры ММФ, БГУ


^ Курсов В.В. – кандидат физико-математических наук, доцент кафедры высшей алгебры ММФ, БГУ


Толкачев М.М.- доцент кафедры высшей алгебры ММФ, БГУ


^ Гаращук М.С. — кандидат физико-математических наук, доцент кафедры высшей алгебры ММФ, БГУ


Одобрена на заседании кафедры

___________________________

протокол № 12 от 19 июня 2007 г.


Одобрена на заседании Ученого совета механико-математического факультета протокол

№ 7 от 20 июня 2007 г.


Ответственный за редакцию: Тавгень Олег Игнатьевич


^ ПОЯСНИТЕЛЬНАЯ ЗАПИСКА


В настоящее время тенденция использования математических методов в других областях знания продолжает ускоренно развиваться и процесс математизации все шире распространяется и на гуманитарные науки, которые традиционно считались неточными. При этом, естественно, повышается роль процесса абстрагирования, необходимого для выделения новых объектов исследования, а на первый план в качестве прикладных выходят те математические методы, которые связаны с понятиями, имеющими достаточно высокую степень общности.

Алгебра, в том виде, который она приобрела за последний период своего развития, проявляет себя как богатый источник таких общих методов. Кроме того, сама идеология алгебраических исследований, принятый в алгебре аксиоматический подход к получению результатов служат образцом для развития частных, прикладных теорий во многих областях науки.

Отмеченные обстоятельства не позволяют более рассматривать алгебру лишь как науку о решении уравнений, использующую формальные символьные методы. Структуру представленного курса определяет необходимость включить в него нетривиальные результаты современной алгебры, касающиеся абстрактных алгебраических объектов. Это позволит студентам, освоившим алгебраические методы исследований, в будущей своей профессиональной деятельности быстрее и легче адаптироваться в новых областях знаний и использовать математику при решении возникающих в них проблем.


^ «АЛГЕБРА И ТЕОРИЯ ЧИСЕЛ»


Цель курса «Алгебра и теория чисел»: обучение студентов фундаментальным методам общей алгебры, линейной алгебры, теории чисел; знакомство с основными алгебраическими структурами — группами, кольцами и полями. Материал дисциплины является опорным для изучения всех общих математических и специальных дисциплин.

При преподавании учебной дисциплины «Алгебра и теория чисел» ставятся следующие задачи:

• ознакомить студентов с фундаментальными понятиями и методами линейной алгебры: теорией матриц, определителей, систем линейных уравнений, векторных пространств и линейных операторов, квадратичных и билинейных форм;
  
• дать введение в задачи и методы общей алгебры: теории групп, колец, полей, теории чисел;
  
• изучить комплексные числа и многочлены;
  
• развить у студентов аналитическое мышление и общую математическую культуру;
  
• привить студентам умение самостоятельно изучать учебную и научную литературу в области математики.
  

Методика преподавания дисциплины строится на сочетании лекций (157 ч.) с практическими занятиями (157 ч.).


^ Тематический план курса «Алгебра и теория чисел»

№ темы	Количество часов
^ Содержание курса	Лекции	Семинарские и практические
Раздел I. Числа, многочлены, матрицы и определители.
1. Арифметика целых чисел.	4	3
2. Алгебраическая операция, основные алгебраические структуры.	2	2
3. Комплексные числа.	5	6
4. Матрицы и операции над ними.	4	4
5. Перестановки и подстановки.	3	3
6. Определители и их применение.	5	6
7. Многочлены от одной переменной.	5	4
8. Сравнения и кольца вычетов.	4	4
Раздел II. Векторные пространства, линейные отображения, билинейные и квадратичные формы.
9. Векторные пространства.	8	8
10. Системы линейных уравнений.	4	6
11. Линейные отображения векторных пространств.	10	10
12. Инвариантные подпространства. Собственные векторы и собственные значения.	6	6
13. Жорданова нормальная форма.	6	6
14. Многочлены от нескольких переменных.	4	4
15. Билинейные и квадратичные формы.	13	13
Раздел III. Пространства с формами, изометрии и основы тензорной алгебры.
16. Евклидовы и унитарные пространства.	8	8
17. Линейные операторы евклидовых и унитарных пространств.	16	16
18. Основы тензорной алгебры.	10	10
Раздел IV. Основные алгебраические структуры.
19. Элементы теории групп.	14	14
20. Кольца и алгебры.	10	10
21. Основы теории полей.	10	10
^ Всего аудиторных часов	157	157
ИТОГО:	314

Раздел I. ЧИСЛА, МНОГОЧЛЕНЫ, МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ


Тема 1. Арифметика целых чисел.


Делимость целых чисел и ее свойства. Теорема о делении с остатком. НОД. Алгоритм Евклида и запись НОД в виде целочисленной линейной комбинации. Взаимно простые числа, критерий. НОК. Простые и составные числа, бесконечность множества простых. Основная теорема арифметики.


^ Тема 2. Алгебраическая операция, основные алгебраические структуры.


Алгебраическая операция. Свойства алгебраической операции: коммутативность и ассоциативность. Нейтральный элемент множества относительно алгебраической операции. Теорема о единственности нейтрального элемента относительно алгебраической операции. Симметричный элемент множества относительно алгебраической операции. Теорема о единственности симметричного элемента относительно ассоциативной алгебраической операции. Определения группы, кольца, поля. Примеры.


^ Тема 3. Поле комплексных чисел.


Определение поля комплексных чисел. Действия в компонентах. Алгебраическая форма комплексных чисел. Комплексное сопряжение. Комплексная плоскость. Модуль и аргумент, их свойства. Тригонометрическая форма записи, связь с действиями. Формула Муавра и ее применение в вещественных вычислениях. Геометрическая интерпретация действий с комплексными числами. Извлечение корня из комплексного числа. Корни из единицы, первообразные корни из единицы. Группа корней из единицы.


^ Тема 4. Матрицы и операции над ними.


Матрица размера m  n. Квадратная матрица порядка n. Диагональная матрица. Единичная матрица порядка n. Нулевая матрица размера m  n. Вектор-строка. Вектор-столбец. Равенство матриц. Сложение матриц, умножение матрицы на скаляр. Умножение матриц. Транспонирование. Свойства матричных операций. Многочлен от матрицы. Элементарные преобразования матриц. Матрицы элементарных преобразований. Теорема о приведении произвольной матрицы к верхней трапециевидной форме.


^ Тема 5. Перестановки и подстановки.


Определения перестановок и подстановок, их число. Инверсии и порядки, четность перестановки. Транспозиции и циклы. Теорема об изменении четности перестановки после применения к ней транспозиции. Умножение подстановок и его свойства. Разложение подстановки в произведение независимых циклов и транспозиций. Четность подстановки. Симметрическая и знакопеременная группы.


^ Тема 6. Определители и их применение.


Определители второго и третьего порядков. Определитель квадратной матрицы произвольного порядка и его свойства. Определитель транспонированной матрицы. Миноры и алгебраические дополнения. Формулировка теоремы Лапласа. Разложение по строке и столбцу. Определитель треугольной матрицы. Методы вычисления определителей. Определитель Вандермонда. Определитель произведения квадратных матриц. Обратная матрица, методы ее вычисления. Невырожденные матрицы, полная линейная группа. Матричная запись линейной системы. Теорема Крамера. Метод Гаусса.


^ Тема 7. Многочлены от одной переменной.


Кольцо многочленов от одной переменной над коммутативным кольцом с единицей. Степень многочлена и ее свойства. Теорема о делении с остатком для многочленов. Алгоритм Евклида, теорема о наибольшем общем делителе многочленов. Взаимно простые многочлены. Неприводимые многочлены. Разложение на неприводимые многочлены. Значение многочлена в точке, функциональное равенство многочленов. Теорема Безу. Схема Горнера. Корень многочлена, теорема о числе корней. Производная многочлена и ее свойства. Кратные корни и производная. Освобождение от кратных корней. Интерполяционная задача, интерполяционная формула Лагранжа. Рациональные корни целочисленного многочлена. Многочлены над полем комплексных чисел. Основная теорема алгебры. Каноническое разложение многочлена над полем комплексных чисел. Многочлены над полем вещественных чисел. Каноническое разложение многочлена над полем вещественных чисел. Простейшие дроби, разложение правильной дроби в сумму простейших.


^ Тема 8. Сравнения и кольца вычетов.


Сравнения и их свойства. Классы вычетов. Теоретико-числовая функция Эйлера, ее мультипликативность. Полная и приведенная системы вычетов. Теоремы Эйлера и Ферма. Решение линейных сравнений от одной неизвестной и их систем, китайская теорема об остатках. Кольцо классов вычетов. Обратимые классы вычетов. Конечные поля.


^ РАЗДЕЛ II. ВЕКТОРНЫЕ ПРОСТРАНСТВА, ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ,

БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ.


Тема 9. Векторные пространства.


Определение и примеры. Система образующих, конечномерные пространства. Линейная независимость векторов. Теорема Штейница о замене. Базис, размерность. Координаты вектора, их изменение при изменении базиса. Матрица перехода, преобразование координат вектора. Подпространство, его размерность. Ранг системы векторов. Ранг матрицы как размерность линейной оболочки ее строк, столбцов. Эквивалентность разных определений ранга. Факторпространство. Сумма и пересечение подпространств, связь их размерностей. Прямая сумма и дополнение подпространств.


^ Тема 10. Системы линейных уравнений.


Матричная запись линейной системы. Метод Гаусса. Теорема Кронекера-Капелли. Число решений линейной системы. Однородные системы, условия существования нетривиального решения. Фундаментальная система решений. Связь между решениями неоднородной и соответствующей однородной систем. Задание подпространства системой линейных уравнений.


^ Тема 11. Линейные отображения векторных пространств.


Линейное отображение, его ядро и образ. Ранг и дефект. Матрица линейного отображения. Алгебраические действия над линейными отображениями. Пространство линейных отображений, связь с матричным пространством. Композиция линейных отображений. Линейная форма, двойственное пространство. Двойственные базисы. Линейный оператор и его матрица. Изменение матрицы оператора при переходе к другому базису. Условия обратимости оператора.


^ Тема12. Инвариантные подпространства. Собственные векторы и собственные значения.


Инвариантное подпространство. Сужение оператора на инвариантное подпространство; индуцированный оператор на факторпространстве. Матрица оператора при наличии инвариантного подпространства, при разложении пространства в прямую сумму инвариантных подпространств. Собственное число и собственный вектор оператора. Характеристический многочлен оператора, теорема Гамильтона-Кэли. Собственное подпространство и его свойства. Оператор, имеющий диагональную матрицу в некотором базисе; критерий диагонализуемости.


^ Тема 13. Жорданова нормальная форма.


Жорданова матрица. Корневой вектор и корневое подпространство. Нильпотентный оператор, его характеристический многочлен. Построение жордановой матрицы нильпотентного оператора. Жорданова матрица произвольного оператора. Циклическое подпространство, клетка Фробениуса. Нормальная форма Фробениуса.


^ Тема 14. Многочлены от нескольких переменных.


Кольцо многочленов от нескольких переменных. Лексикографический порядок. Отсутствие делителей нуля. Симметрические многочлены. Основная теорема о симметрических многочленах.


^ Тема 15. Билинейные и квадратичные формы.


Билинейная и полуторалинейная форма на линейном пространстве, их матрица. Матрица Грама., ранг формы. Эрмитовы и симметрические билинейные формы, их матрицы Грама. Ортогональность относительно билинейной симметрической формы, существование ортогонального базиса. Квадратичная форма и ее матрица. Квадратичная форма как однородный многочлен. Канонический вид. Приведение квадратичной формы к каноническому виду методом Лагранжа. Нормальный вид вещественной и комплексной квадратичных форм. Закон инерции квадратичных форм. Критерий Сильвестра положительной определенности квадратичной формы. Знакоопределенные квадратичные формы. Полуторалинейные и эрмитовы формы.


^ РАЗДЕЛ III. ПРОСТРАНСТВА С ФОРМАМИ, ИЗОМЕТРИИ И ОСНОВЫ ТЕНЗОРНОЙ АЛГЕБРЫ.


Тема 16. Евклидовы и унитарные пространства.


Определение евклидова и унитарного пространства. Длина вектора, угол между векторами. Неравенство Коши-Буняковского. Ортонормированные семейства векторов. Ортонормированные базисы. Процесс ортогонализации Грама-Шмидта. Ортогональное дополнение к подпространству в евклидовом или унитарном пространстве. Разложение пространства в ортогональную прямую сумму.


^ Тема 17. Линейные операторы евклидовых и унитарных пространств.


Сопряженный оператор, его существование и свойства. Инвариантные подпространства для сопряженных операторов. Условие ортонормальной диагонализуемости оператора. Нормальный оператор в унитарном и евклидовом пространстве. Унитарные и ортогональные операторы, канонический вид их матриц. Унитарная и ортогональная группы. Самосопряженный оператор. Существование ортогонального преобразования, приводящего вещественную квадратичную форму к диагональному виду. Пары форм. Полярное разложение.


^ Тема 18. Основы тензорной алгебры.


Тензорное произведение векторных пространств: определение, примеры, расширение поля скаляров, произведение операторов. Тензорная алгебра векторного пространства, тензоры типа (p,q), градуировка. Симметрическая алгебра: симметрическая степень пространства, симметрическое произведение функций, симметрическая степень линейного оператора. Алгебра Грассмана: внешняя степень пространства, алгебра Грассмана и теория определителей.


^ РАЗДЕЛ IV. ОСНОВНЫЕ АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ.


Тема 19. Элементы теории групп.


Определение группы, подгруппы, примеры. Гомоморфизм, изоморфизм, автоморфизм. Порядок элементов. Циклические группы, классификация. Умножение подмножеств в группе. Смежные классы по подгруппе, разложение Лагранжа, индекс подгруппы. Теорема Лагранжа о группах, следствие о порядке элемента. Нормальная подгруппа. Факторгруппа. Ядро и образ гомоморфизма. Первая (основная) теорема о гомоморфизме, ее применение к вычислению факторгруппы. Связь подгрупп факторгруппы и промежуточных подгрупп. Вторая и третья теоремы о гомоморфизме. Прямое произведение групп и разложение группы в прямое произведение своих подгрупп. Формулировка теоремы о строении конечно порожденной абелевой группы. Подгруппа и нормальная подгруппа, порожденные данным множеством. Центр и коммутант. Критерий абелевости факторгруппы.


^ Тема 20. Кольца и алгебры.


Определение кольца, подкольца, примеры. Гомоморфизм, изоморфизм, ядро гомоморфизма. Идеалы колец. Факторкольца. Основная теорема о гомоморфизме для колец. Главные идеалы. Идеалы в 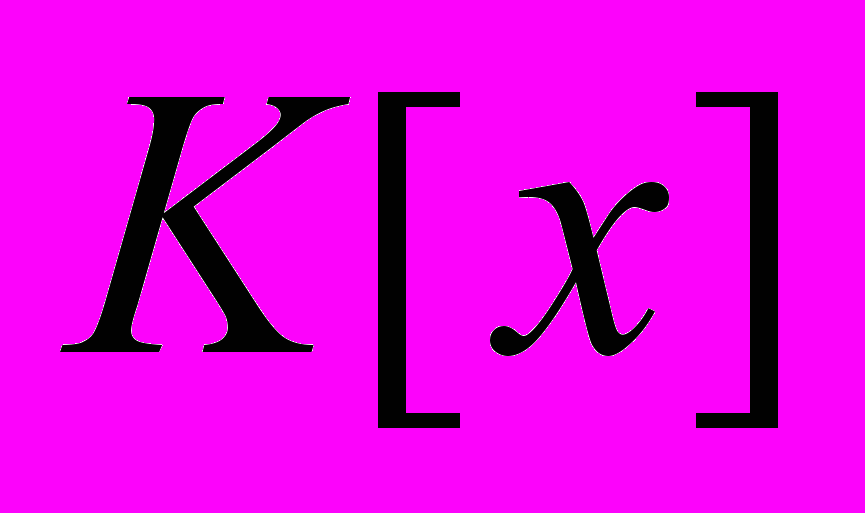и 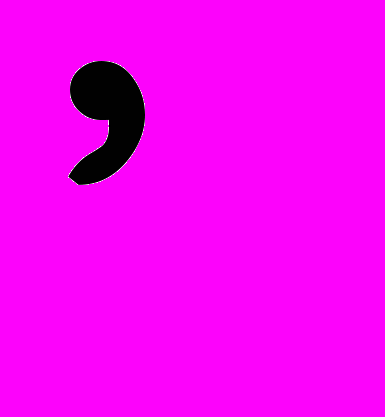. Простые и максимальные идеалы, соответствующие факторкольца. Прямое произведение колец. Строение кольца 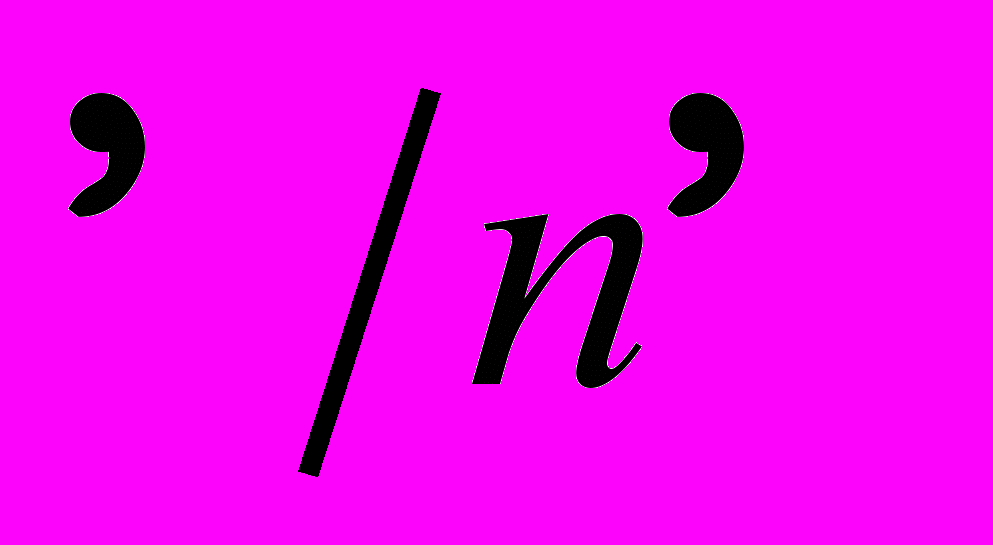. Алгебры, тела. Кватернионы.


^ Тема 21. Основы теории полей.


Определение поля, подполя, расширения, примеры. Характеристика поля. Простые поля, классификация. Расширение подполя, получающееся присоединением подмножества большего поля; простое расширение. Конечное расширение, степень расширения. Мультипликативность степени. Алгебраические и трансцендентные элементы. Минимальный многочлен алгебраического элемента. Алгебраические расширения, алгебраичность конечного расширения. Простое расширение, порожденное алгебраическим элементом; присоединение к полю корня неприводимого многочлена. Поле разложения многочлена, существование и единственность. Поле разложения семейства многочленов. Алгебраически замкнутые поля, алгебраическое замыкание. Существование трансцендентных чисел. Поле рациональных функций. Простое расширение, порожденное трансцендентным элементом. Число элементов конечного поля. Конечное поле как поле разложения. Мультипликативная группа конечного поля. Существование и единственность поля, содержащего данное число элементов. Подполя конечного поля. Неприводимые многочлены над конечным полем.


ЛИТЕРАТУРА

^ ПО КУРСУ «АЛГЕБРА И ТЕОРИЯ ЧИСЕЛ»


ОСНОВНАЯ:

1. Винберг Э.Б. Курс алгебры. М.: Факториал-пресс, 2001.
   
2. Виноградов И.М. Основы теории чисел. М.: Наука, 1976.
   
3. Кострикин А.И. Введение в алгебру. Т. 1-3. М.: Физ.-мат. литература, 2000-2001.
   
4. Курош А.Г. Курс высшей алгебры. М.: Наука, 1965 (и более поздние издания).
   
5. Мальцев И.М. Основы линейной алгебры. М.: Наука, 1970.
   
6. Милованов М.В., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. Т. 1. Мн.: Амалфея, 2001.
   
7. Милованов М.В., Толкачев М.М., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. Т. 2. Мн.: Амалфея, 2001.
   
8. Фаддеев Д.К. Лекции по алгебре. М.: Наука, 1984.
   

ДОПОЛНИТЕЛЬНАЯ:

1. Айерлэнд К., Роузен М. Классическое введение в современную теорию чисел. М.: Мир, 1987.
   
2. Бейкер А. Введение в теорию чисел. Мн.: Вышэйшая школа, 1995.
   
3. Ван дер Варден Алгебра. М.: Наука, 1976.
   
4. Гельфанд И.М. Лекции по линейной алгебре. М.: МЦНМО, 1998.
   
5. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. М.: Наука, 1972.
   
6. Кокс Д., Литтл Дж., О’Ши Д. Идеалы, многообразия и алгоритмы. М., Мир, 2000.
   
7. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. М.: Наука, 1983.
   
8. Ленг С. Алгебра. М.: Мир, 1968.
   
9. Прасолов В. В. Многочлены. М.: Мир, 2000.
   

ЗАДАЧНИКИ:

1. Бурдун А.А., Мурашко Е.А., Толкачев М.М., Феденко А.С. Сборник задач по алгебре и аналитической геометрии. Мн.: Унiверсiтэцкае, 1999.
   
2. Проскуряков И. В. Сборник задач по линейной алгебре. М.: Наука, 1974.
   
3. Фаддеев Д. К., Соминский И. С. Сборник задач по высшей алгебре. М.: Наука, 1977.
   
4. Сборник задач по алгебре. Под ред. А. И. Кострикина. М.: Наука, 1987.