Самообразования Проверка знаний, умений и навыков

Вид материала

Документы

Содержание Еречень модулей Противоречия и затруднения, решаемые в данном опыте. Педагогическое кредо V. Результативность. VI. Трудоёмкость. VII. Доступность. VIII. Описание опыта. Обучающая функция проверки Сущность диагностической функции проверки Развивающая функция проверки Сущность ориентирующей функции проверки Сущность воспитывающей функции проверки Объективность проверки При индивидуальной проверке При групповой проверке Текущая проверка При тематической проверке Итоговая проверка Второй вид Среди методов проверки ... Полное содержание

Подобный материал:

• Задача обучения сводится не к формированию знаний, умений, навыков, а к развитию способностей, 119.59kb.
• Г. А. Яленская «3» июня 2011 г. Положение об областном конкурс, 48.09kb.
• Лекция 4 (2 часа) Проектирование профессионального самообразования, 131.09kb.
• Модель оценки индивидуальных достижений учащихся, основанная на компетентностном подходе, 38.33kb.
• Тема проверки: Сформировать ведущих знаний, умений, навыков по математике, 259.42kb.
• Министерство здравоохранения СССР приказ 21 июля 1988 г. N 579 об утверждении квалификационных, 5835.08kb.
• Л. Ф. Методы и формы контроля усвоения знаний учащихся по русскому языку Рассказ (сообщение,, 273.63kb.
• Приказ Минздрава СССР от 21 июля 1988 г. N 579 "Об утверждении квалификационных характеристик, 6761.86kb.
• Следует отметить, что среди очень близких по значению понятий «контроль», «проверка»,, 52.57kb.
• Примерные проверочные работы по русскому языку, 100.32kb.

Министерство образования и науки РФ

МОУ «Трусовская средняя общеобразовательная школа»

Курьинского района, Алтайского края











ИЗ ОПЫТА РАБОТЫ УЧИТЕЛЯ
МАТЕМАТИКИ
МОУ «ТРУСОВСКАЯ СРЕДНЯЯ
ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»







П ЕРЕЧЕНЬ МОДУЛЕЙ

• Условия возникновения, становления опыта;
  

• Противоречия и затруднения, решаемые в данном опыте;
  

• Целеполагание;
  

• Теоретическая база опыта;
  

• Результативность;
  

• Трудоёмкость;
  

• Доступность;
  

• Описание опыта;
  

1. 
   Условия возникновения, становления опыта.
   

Опыт формировался в условиях сельской общеобразовательной школы, которая функционирует с 1979 года. Веду уроки математики в 5 - 11 классах. Тема самообразования «Проверка знаний, умений и навыков учащихся на уроках математики». Над данной темой работаю 3 года.

2. Противоречия и затруднения, решаемые в данном опыте.
   

Опыт является актуальным для большинства учителей математики. Он направлен на преодоление следующих трудностей:

• шаблон в преподавании предмета;
  
• потеря интереса к предмету;
  
• низкий уровень мотивации при оценке, самооценке и взаимооценке учащихся;
  

3. Целеполагание.
   

Ведущей идеей опыта является стимулирование учебно – познавательной деятельности каждого ученика на основе применения элементов инновационных технологий. Моё жизненное кредо - «Не говори «малоспособен», а говори «способности не раскрыты».

Основной целью работы считаю достижение оптимальных результатов обучения учащихся по каждой теме.

Ссылаясь на слова Дж. Пойта «Главная задача математической программы,- научить детей мыслить», выделяю для себя следующие

педагогические принципы:

• учет индивидуальных особенностей и уровня подготовленности ученика и класса;
  
• реализация внутрипредметных и межпредметных связей;
  
• обеспечение нарастания сложности учебного материала при выводе формул, математических законов, выполнении упражнений;
  
• использование широкого кругозора по математике одних учащихся, как источник дополнительных знаний для других.
  

ПЕДАГОГИЧЕСКОЕ КРЕДО: «НЕ ОЦЕНИВАТЬ, А ЦЕНИТЬ».


IV. Теоретическая база опыта.

В своей работе руководствуюсь теорией оптимизации учебно-воспитательного процесса Ю.К. Бабанского, теорией развития познавательных интересов Г.Н. Щукиной, творчески использую идеи В.Ф. Шаталова, опираюсь на методику изложения авторов УМК Н.Я. Виленкина.

При организации учебно-воспитательного процесса использую технологию личностно-ориентированного образования школьников, разработанную И.С. Якиманской, теорию активизации учебной деятельности И.Ф. Харламова, в содержании которой рассматриваются:

• мотивация учения;
  
• активные методы обучения;
  
• применение форм, активизирующих учение;
  
• создание благоприятного психологического климата на уроке;
  
• развитие творческих способностей учащихся;
  

Главное в педагогике - развитие ребенка, прежде всего нравственное развитие, а обучение - это средство, а не цель.

План учебный: осмысливается и запоминается учеником то, что так или иначе проходит через его собственную познавательную деятельность, к чему он приложил мыслительные усилия, на что затратил нервно-психическую энергию. Нельзя научить решать задачи, а можно только научиться их решать. Учу детей и сама учусь, ведь авторитет – дело временное, а основная миссия учителя – сеять доброе в пределах вечного.

У Ушинского читаем о том, что мечтать легко и приятно, а мыслить, думать - трудно.

Существует немало учащихся, не обладающих достаточной природной одаренностью к изучению математики, но имеющих желание и прилежание и в силу этого способных одолеть данный курс. Поэтому стремлюсь познавательную деятельность детей, в которой первостепенное внимание уделяется развитию трудолюбия, интереса к предмету, активности и самостоятельности через организацию общения и совместной деятельности для максимальной реализации их потенциальных возможностей.

V. Результативность.

• устойчивый интерес к предмету;
  
• благоприятные морально – психологические условия взаимодействия всех участников образовательного процесса;
  
• стабильность результатов: на «4» и на «5» успевает 50% учащихся; вовлечение учащихся в проведение научно-исследовательских работ на основе практических работ на местности.
  

VI. Трудоёмкость.

Требуется высокая профессиональная самоотдача учителя. Дополнительные затраты времени на разработку методического и дидактического обеспечения уроков.


VII. Доступность.

Идеи опыта могут быть использованы учителями-предметниками, желающими получить удовлетворение от своей работы и стремящимися раскрыть весь потенциал ученической работоспособности.


VIII. Описание опыта.


« Что нам нужно, чтобы добиться успеха?

Ничего не уничтожать и совершенствовать

имеющееся».

Н. И. Лобачевский


Для выяснения роли проверки в процессе обучения математике рассмотрим ее наиболее значимые функции: контролирующую, обучающую, диагностическую, развивающую, ориентирующую и воспитывающую.

Сущность контролирующей функции проверки заключается в выявлении состояния знаний и умений учащихся, уровня их умственного развития, в изучении степени усвоения приемов познавательной деятельности, навыков рационального учебного труда.

При помощи контроля определяется исходный уровень для дальнейшего овладения знаниями, умениями и навыками, изучается глубина и объем их усвоения, сравнивается планируемое с действительными результатами. На этой же устанавливается эффективность используемых учителем методов, форм и средств обучения.

Обучающая функция проверки заключается в совершенствовании знаний и умений, их систематизации. Например, формирование навыков самоконтроля осуществляется, прежде всего, через проверку действий ученика преподавателем. В процессе проверки учащиеся повторяют и закрепляют изученный материал. Они не только воспроизводят ранее изученное, но и применяют знания и умения в новой ситуации, мобилизуют определенные способы решения задач, определенные приемы учебно-познавательной деятельности.

Проверка помогает учащимся выделить главное, основное в изучаемом, уточнить содержание рассматриваемого вопроса, сделать проверяемые знания и умения более ясными, точными и действенными. Проверка способствует обобщению и систематизации знаний, выработке соответствующих данному этапу обучения умений и навыков.

Сущность диагностической функции проверки состоит в получении информации об ошибках, недочетах и пробелах в знании и умениях учащихся и порождающих их причинах. Здесь важно получить информацию не только о причинах данного состояния знаний учащихся, но и о степени влияния этих причин на качество знаний, умений и навыков учащихся.

Результаты диагностических проверок дают материал об истоках затруднений учащихся в овладении учебным материалом, о числе, характере и причинах ошибок, что позволяет выбрать наиболее действенной методики обучения и в общем плане уточнить направление дальнейшего совершенствования содержания, методов и средств обучения

Развивающая функция проверки состоит в стимулировании познавательной активности учащихся, в развитии их творческих сил и способностей. В процессе проверки развивается речь, память, внимание, воля, воображение и мышление школьников.

Проверка обладает исключительными возможностями в развитии учащихся. В процессе проверки развивается речь, память, внимание, воображение, воля и мышление школьников. Проверка оказывает большое влияние на развитие и проявление таких качеств личности, как способности, склонности, интересы, потребности, отношения и др. Оказывая влияние на развитие учащихся, проверка одновременно представляет богатую информацию об уровне этого развития.

Сущность ориентирующей функции проверки - в получении информации о степени достижения цели обучения отдельным учеником и классом в целом - насколько усвоен и как глубоко изучен учебный материал.

Проверка ориентирует учащихся в их затруднениях и достижениях. Вскрывая пробелы, ошибки и недочеты учащихся, она указывает им направления приложения сил по совершенствованию знаний и умений. Проверка помогает учащимся лучше узнать самого себя, оценить свои знания и возможности. Проверка ориентирует и учителя в недочетах и достижениях его преподавания. Она содействует выявлению и обобщению передового педагогического опыта и служит также цели государственного контроля за работой школ и учителей.

Сущность воспитывающей функции проверки заключается в воспитании у учащихся ответственного отношения к учению, дисциплины, аккуратности, честности.

Проверка побуждает учащихся более серьезно и регулярно контролировать себя при выполнении заданий, она является условием и стимулом воспитания твердой воли, настойчивости, привычки к регулярному труду.

Выделенные функции проверки подчеркивает ее роль и значение в процессе обучения. В учебном процессе сами функции проявляются в разной степени и в различных сочетаниях. Это зависит в основном от целевого назначения и вида проверки, причем цели проверки обусловливаются планируемыми на данном этапе обучения дидактическими, развивающими и воспитывающими целями и в конкретном виде проверки воплощаются определенные их сочетания. Реализация выделенных функций на практике делает проверку более эффективной, а вместе с ней эффективной становится и сам учебный процесс.

Проверка должна быть целенаправленной, объективной, всесторонней, регулярной и индивидуальной.

Целенаправленность предполагает четкое определение цели каждой проверки. Постановка цели является звеном, определяющим всю последующую работу по обоснованию используемых формул, методов и средств проверки. Цели проверку включают: что должно проверяться? Кто должен опрашиваться? Какие выводы можно будет сделать на основе результатов проверки? При конкретизации целей проверки исходя из целей воспитания, развития и обучения учащихся, реализуемых на данном этапе обучения.

Объективность проверки предупреждает случаи субъективных и ошибочных суждений, искажающих действительную успеваемость учащихся и снижающих воспитательное значение проверки. Объективность проверки зависит от многих факторов. Среди них выделяют следующие: четкое выделение общих и конкретных целей обучения, разработанность требований к знаниям, умениям, навыкам учащихся, обоснованность выделения и отбора объектов и содержания проверки, адекватность проверочных заданий целям проверки, обеспеченность методами обработки, анализа и оценивания результатов проверки, организованность проведения проверки и др. От решения этих вопросов во многом зависит объективность и качество проверки.

Под всесторонностью проверки понимается охват большого по содержанию проверяемого материала: это и усвоение основных идей данного курса, и усвоение учебного материала по определенным содержательным, стержневым линиям курса, и знание учащимися отдельных и существенных фактов, понятий и закономерностей, теорем, способов действий и способов деятельности. Ясно, что при таком обилии проверяемого материала усложняется методика составления заданий, т.е. предъявляются повышенные требования к методике выделения и отбора объектов проверки.

Под регулярностью подразумевается систематическая проверка, органически сочетающаяся с самим учебным процессом.

Индивидуальность проверки требует проверки и оценки знаний, умений и навыков каждого школьника.

В соответствии с формами обучения на практике применяются следующие формы проверки: индивидуальная, групповая (вместе с разновидностью – уплотненным опросом), фронтальная (вместе с массовыми проверками).

При индивидуальной проверке каждый ученик получает свое задание, которое он должен выполнить без посторонней помощи. При этом ученик показывает результаты самостоятельной умственно-практической деятельности. Учитель выявляет правильность ответа, его последовательность, полноту и глубину, самостоятельность суждений и выводов, степень развития логического мышления, культуру речи и т.п.

Учитывая значение и многофункциональность проверки, на практике стремятся охватить индивидуальной проверкой каждого ученика класса, причем неоднократно. В связи с этим индивидуальная проверка всегда планируется: учитель намечает, когда, кого, с какой целью спросить, какие для этого использовать средства.

При групповой проверке класс временно делится на несколько групп (от 2 до 10 учащихся) и каждой группе дается проверочное задание. В зависимости от цели проверки группам предлагают одинаковые задания или дифференцированные: проверяют результаты письменно-графического задания, которое ученики выполняли по двое, или практического, выполняемого каждой четверкой учащихся, или проверяют точность, скорость и качество выполнения конкретного задания (в форме дидактической игры или соревнования) по звеньям. Групповую форму организации проверки применяют при повторении с целью обобщения и систематизации учебного материала, при выделении приемов и методов решения задач, при акцентировании внимания учащихся на наиболее рациональных способах выполнения заданий, на лучшем из вариантов доказательства теоремы. Оценивание в баллах групповой работы производится не всегда, иногда достаточно слова, отзыва, рецензии. Хорошо продуманная групповая проверка создает благоприятные возможности для развития и воспитания учащихся. Иногда групповую проверку проводят в виде уплотненного опроса; несколько учеников отвечают устно у доски или письменно за партами.

При устной проверке иногда провожу опрос в звене: одновременно вызываются несколько учащихся, которые получают задания, логически связанные между собой. Последовательный ответ на них используется всем классом для повторения материала по проверяемому разделу. При фронтальной проверке задания предлагаю всему классу. Меня интересует сознательность в ответах учащихся, обоснованность. Наблюдаю за аккуратностью выполнения заданий, вскрываю слабые стороны в знаниях учащихся, обнаруживаю недочеты, пробелы, ошибки в работах и ответах учащихся. Это позволяет вовремя наметить меры по их преодолению и устранению.

При фронтальной проверке задания предлагаются всему классу. В процессе этой проверки изучается правильность восприятия и понимания учебного материала, качество словесного, графического, предметного оформления, степень закрепления в памяти. Учителя интересует сознательность в ответах учащихся, обоснованность и доказательность. Он наблюдает за аккуратностью выполнения заданий, вскрывает слабые стороны в знаниях учащихся, обнаруживает недочеты, пробелы, ошибки в работах и ответах учащихся. Это позволяет ему вовремя наметить меры по их преодолению и устранению.

К основным видам проверки знаний, умений и навыков учащихся по математике относят текущую, тематическую, итоговую проверки.

Текущая проверка проводится на каждом уроке, причем почти на каждом его этапе. Здесь и проявляются наиболее ярко все функции проверки. Поэтому текущая проверка требует от учителя большого внимания, чуткости и тактичности. Текущая проверка содействует отработке и шлифовке знаний и умений. Оценивать нужно осторожно. Все мы знаем, что объективная оценка может поддержать, подбодрить ученика, поспешно выставленная – задержать, затормозить. Оценка считается педагогически правильной, если она стимулирует дальнейшее развитие личности. Поэтому при оценивании слабых учащихся можно использовать отсроченный контроль, когда оценку ставят им после усвоения проверяемых знаний.

При тематической проверке выясняется усвоение учащимися положений темы. Здесь внимание уделяется выявлению умений учащихся связно и последовательно излагать усвоенный материал, умений обобщать, умений применять знания при решении практических и познавательных задач.

Проведение тематической проверки во многом зависит от четкого выделения в теме основных разделов или подтем. Число подтем определяет частоту этого вида проверки, и на практике она осуществляется через систему кратковременных контрольных или самостоятельных проверочных работ. На основе результатов тематической проверки, включая результаты контрольной работы по теме, выставляются оценки за четверть, полугодие, учебный год. Задания для проведения контрольной работы в основном берутся из дидактических материалов. Но в любую контрольную работу можно включить еще одно задание, с которым могут справиться только отдельные ученики. Все задания, входящие в контрольную работу, полностью согласуются со школьной программой. Контрольная работа позволяет узнать, есть ли у учащихся типичные пробелы в их знаниях и умениях, выявить уровень развития мышления.

На основе результатов тематической проверки, включая результаты контрольной работы по теме, выставляются оценки за четверть, полугодие, учебный год.

Для более успешной реализации принципа преемственности в процессе преподавания математики я практикую проведение учета знаний учащихся методом зачета. При необходимости провожу консультацию по данной теме.

Карточки – задания у меня трех цветов. Карточки желтого цвета рассчитаны для слабых учащихся, туда я включаю задания обязательного уровня; за правильное выполнение задания ученик получает оценку «3». Карточки зеленого цвета – для учащихся среднего уровня; карточки красного цвета – для учащихся, обучающихся на «5», туда я включаю дополнительно задания посложнее.

Для проведения зачета в пятых – седьмых классах использую стенд с прикрепляющимися карманами для заданий. Для удобства хранения его можно сделать в виде складывающейся книги. Зачет в виде игры «Математические тяжеловесы» является своеобразным конкурсом по решению задач. В каждый карман кладется набор карточек заданий: в один карман – задачи одинаковой трудности, в разные – различной. Сложность задач «оценивается» килограммах. Поэтому на каждом кармане пишется «вес содержимых задач»: 30кг, 40кг, 50кг.

По команде учителя ученики выходят и без спешки, по одному, берут по одной задаче из любого кармана. Ученик, решивший задачу, подходит к учителю и объясняет свое решение. Если задача решена правильно, то «вес» считается взятым, и ученик допускается к «взятию» большого веса. Если в задаче допущена ошибка, то предлагается ее заменить задачей этого же «веса».

Зачетный урок предназначен не только для контроля знаний и умений учащихся, а прежде всего для обучения, развития учащихся посредством индивидуальной работы с каждым школьником непосредственно на зачете. В зачет включается тот материал, которым после изучения темы должны владеть все ученики класса. Существенно, чтобы в ходе зачета можно было установить наличие знаний, умений, навыков, которые необходимы школьникам для изучения последующих тем. Кроме того, целесообразно включать такой материал, который входит в программу выпускных и вступительных экзаменов, так как одна из целей зачета – подготовка школьников к ЕГЭ.

При дифференцированном подходе к обучению содержание контроля и оценка должны отражать принятый уровневый подход. Контроль должен предусматривать проверку достижения всеми учащимися ОРО, а так же дополняться проверкой усвоения материала на более высоких уровнях.

Для выполнения этого условия целесообразно в контрольных и проверочных самостоятельных работах давать задания различного уровня сложности. Перед началом работы учащимися сообщается, какие задания относятся к базовому уровню, а какие к повышенному.

После изучения каждой темы курса так же проводится зачёт. В этом случае каждый зачёт состоит из двух частей: обязательный и дополнительный.

Обязательная часть зачёта нацелена на проверку достижения обязательного уровня усвоения материала всеми учащимися. По её выполнению определяется, сдал учащийся зачёт (достиг обязательного уровня овладения темой) или не сдал его.

Дополнительная часть зачёта направлена на проверку овладения темой на повышенном уровне. Её выполнение позволяет ученику получить одну из оценок «4» или «5». Основное назначение дополнительной части - дифференцировать учащихся по уровню их подготовки, а также стимулировать школьников, которым хорошо даётся предмет. Зачёты проводятся по каждой из тем курса. Лишь в этом случае, то они не будут иметь дисциплинирующего и организующего влияния на учащихся на других этапах обучения, когда формируются необходимые знания и умения.

Зачёты сдаются всеми учениками, в том числе и теми, кто имеет по математике оценки «4» и «5», так как у сильных учеников бывают пробелы именно в основных умениях. Соответствующие недоработки всплывают именно во время зачёта и подготовки к нему, что позволяет учителю и самому ученику своевременно обратить на них внимание.

Зачёт лучше проводить не на последнем уроке темы. Желательно спланировать работу так, чтобы после зачёта оставалось время для ликвидации обнаруженных недочётов.

Зачёты могут проводиться в различной форме. Если он проводится письменно, то его организация напоминает обычную контрольную работу: ученик получает задание, выполняет его в отведённое время, сдаёт учителю на проверку. Отличие зачёта состоит лишь в его содержании и необходимости его пересдачи в случае отрицательного результата.

При устной форме зачёта учащийся, как на устном экзамене, получив задание, некоторое время готовится к ответу по нему, делает все необходимые записи.

При смешанной форме зачёта часть учащихся класса можно опросить устно, а остальным предложить сдать тетради с выполненными заданиями на проверку учителю.

Каждая из указанных форм проведения зачёта обладает своими преимуществами и недостатками. Письменный зачёт позволяет одновременно охватить проверкой большое число учеников. Кроме того, задачи, связанные с вычислительной работой, требуют письменного выполнения. Устные ответы более целесообразны там, где требуются обширные пояснения.

Возможна такая организация проверки, когда ученик уже в ходе зачёта узнаёт, успешно ли он справился с обязательной частью работы. Выполнив обязательные задачи, ученики по очереди подходят к учителю для проверки. Учитель просматривает работу и отмечает в тетрадях учеников верное решение знаком «+» и указывает на необходимость исправления неверного решения.

За успешное выполнение любого задания из обязательной части работы выставляется 1 балл. Этим подчёркивается равноценность всех заданий с точки зрения формирования опорных, базовых знаний и умений. За задания дополнительной части выставляется различное число баллов.

Для того чтобы задание было засчитано, необходимо, чтобы оно было выполнено полностью и без ошибок.

Выполнение зачётной работы оценивается в соответствии с критериями, разработанными для каждого зачёта. В них указывается число баллов, которое должен набрать ученик, чтобы получить ту или иную оценку по каждому зачёту.

Выполнение обязательной части зачёта оценивается по двухбалльной шкале: «зачтено» - «не зачтено». Но в школьной системе не предусмотрено выставление таких оценок. Поэтому оценка «зачтено» соответствует оценке «3», «не зачтено» - «2». А так как каждый ученик имеет право пересдать зачёт, если получил «не зачтено», то оценка «2» учителем практически не выставляется.

Выполнение дополнительной части оценивается только в том случае, если ученик набрал нужное число баллов по обязательной части.

Для получения каждой из оценок «4» или «5» указывается два критических значения; не только число баллов, которое нужно набрать за выполнение дополнительных заданий, но и число баллов, которое требуется набрать по обязательной части.

Поясним это на примере зачёта по математике в 5 классе.

Зачет№1

Натуральные числа. Сложение и вычитание натуральных чисел.

Обязательная часть

1. Какое из чисел больше: 5221 или 5218?

2. Начертите числовой луч, отметьте на нём точки, которые изображают числа 3 и 10.

3. Запишите в порядке убывания числа: 878, 778, 887, 787.

4. Вычислите: а)7661+93053; б)6007-574.

5. Найдите значение выражения: (175 + 280) - (180 + 95).

6. Верно ли выполнены действия:

а) 2673+1476=5149

б) 7421-3240=1181?

7. За три дня туристы должны пройти 70 км. В первый день они прошли 25 км, во второй - на 6 км больше. Сколько километров осталось пройти туристам?

8. В автопарке 246 легковых и грузовых автомобилей. Из них 128 грузовых. Каких автомобилей меньше и на сколько?

9. Я задумала число. Если его увеличить на 15, то получится 64. Какое число я задумала?

Дополнительная часть

10. (3 балла). Запишите все трёхзначные числа, в записи которых используются цифры 0,2 и 9 без повторения. На сколько наибольшее из этих чисел больше наименьшего?

11. (3 балла). Замените звёздочки (*) подходящими цифрами:


1 * 9 *

+

* 0 * 5

* 1 0 6 7

12. (5 баллов).

Решите задачу без составления уравнения:

«В автобусе ехало несколько пассажиров. На первой остановке вышли 12 и вошли 7 пассажиров. На второй остановке вышли 5 и вошли 8 пассажиров, после чего в автобусе стало 40 пассажиров. Сколько их было до первой остановки?

13. (5 баллов).

Подчитайте точное число прямоугольников:

Каждое обязательное задание оценивается одним баллом, два дополнительных задания по 5 баллов. Критерии оценивания зачёта приведены в таблице:

Отметка	«зачёт»	«4»	«5»
Обязательная часть	7 баллов	8 баллов	9 баллов
Дополнительная часть		3 балла	5 баллов

Для получения оценки «зачёт» ученику достаточно набрать, как минимум 7 баллов, т.е. выполнить верно любые 7 из девяти обязательных заданий. При этом неважно, как выполнит ученик оставшиеся два задания: верно, неверно или не выполнит совсем.

Для того чтобы получить оценку «4», ученик должен набрать не менее 8 баллов по обязательной части и получить хотя бы 3 балла по дополнительной части (т.е. достаточно справиться хотя бы с одним дополнительным заданием, которое оценивается 3-мя баллами).

Для получения оценки «5» ученик должен тоже набрать не менее 8 баллов по обязательной части и получить хотя бы 5 баллов по дополнительной части (например, справиться с двумя более простыми заданиями или одним более сложным).

В тех случаях, когда учитель видит, что данные критерии слишком высоки, что учащиеся класса не в состоянии выполнить предъявляемые к ним требования, желательно провести коррекцию критерия. Например, учитель может уменьшить число баллов, необходимое для получения оценки «зачёт».

Коррекцию критерия нужно проводить до зачёта, а не в ходе его проведения или проверки. Изменённый критерий доводится до сведения учеников. Для выставления оценок за зачёт учащиеся в тетрадях, где у них записаны вопросы и задания к зачёту заполняют таблицу, где в первой строке обозначены номера заданий, во второй строке - ставится знак «+» напротив задания, которое выполнено верно. В результате учителю легко оценить работу каждого ученика. В этой же таблице можно отвести графу для выставления оценки за теоретический материал темы.

Если ученик не получил «зачёт» за обязательную часть, то он должен эту часть пересдать.

Пересдать нужно не все задания обязательной части, а только те, с которыми ученик не справился. Для этого учитель подбирает аналогичные задания.

Проводить пересдачу дополнительной части, если ученик сразу не набрал необходимого числа баллов не обязательно. Ученики сразу знакомятся с условием, что повышенную оценку они должны заработать сразу, без пересдачи.

Для снижения перегрузки можно пересдачу зачёта проводить на других уроках, не выделяя для этого времени после уроков. Например, задачу, аналогичную той, с которой ученик не справился на зачёте можно предложить ему в качестве дополнительного задания или при устном опросе, или во время

самостоятельной работы, или при проверке домашнего задания.


Каковы же преимущества зачетных уроков? Контрольная работа фиксирует незнание, но не позволяет оказать дифференцированную и своевременную помощь. Во время обычных уроков многие остаются неопрошенными по теме, а некоторые слабые учащиеся, получив «2» по одной теме, «исправляют» эту оценку во время опроса совсем по другой теме. Это приводит к тому, что «хвост» незнания только нарастает. В этом отличительная особенность математики как учебного предмета – не имея хороших знаний по одной теме, трудно усвоить следующую. При обычном опросе страдают «способные» учащиеся, ибо учитель вынужден акцентировать внимание на материале, который вызвал затруднение у их одноклассников. Сильным это не интересно. Еще хуже то, что сильные без особых усилий постоянно получают пятерки, хотя трудозатраты их минимальны.

Зачетные уроки полезны и для учителя. Дело не только в том, что он практически не может опросить каждого ученика так, как это происходит на зачете, сколько в том, что эти 45 минут вносят существенный вклад в обучение, развитие и воспитание каждого из 20-25. Не менее важно и то обстоятельство, что учитель теперь получает возможность преодолевать типичную ситуацию: у доски «мается» слабый ученик, а учитель и класс с нетерпением ждут развязки. При этом класс старается помочь ученику, учителю приходится поощрять это, а драгоценное время урока истекает.



Итоговая проверка носит специализированный характер. Она проводится в форме годовых контрольных работ, экзаменов в 9 классах и единых государственных экзаменов в 11 классах. На ЕГЭ внедрена система тестирования. Эта система, которая устанавливает обратную связь в учебном процессе, при этом оцениваются знания и умения учащихся за курс средней школы.

Опрос по теме, заданной для повторения или изучения может заменить математический диктант. Минут на 10 (в зависимости от того, как важна, велика повторяемая тема) даю учащимся математический диктант. При составлении текстов математического диктанта принимаю во внимание особенности и возможности учащихся. Для учащихся седьмого класса по алгебре и геометрии можно применять готовые звуковые приложения.

Для проверки знаний учащихся применяю задания с выборочной формой ответа. Такие карточки – задания способствуют выработке у учащихся устойчивых навыков в усвоении различных математических понятий, их свойств, правил действий.

Пример. Линейные функции:

1. Какие из данных функций являются линейными:

а) у = х (3+2х); б) у=7х+5; в) у = г) у=4 - .

2. Через какие точки А, В,С, D проходит график функции, заданной формулой

у = -?

а) А(5;0); б) В(-5;4); в) С(-25;0); г) D(-10;7)

3. График какой из приведенных функций образует с положительным направлением оси ОХ тупой угол?

а) у=3х - 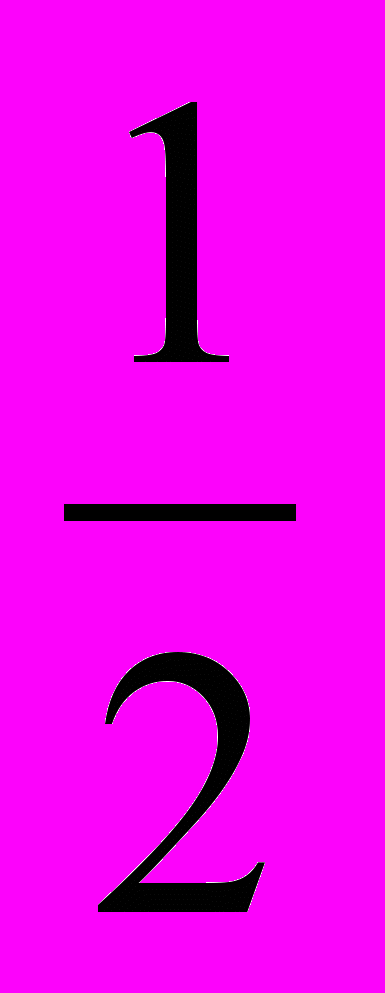; б) у = - ; в) у=-4+2х; г) у=-7х-2. 4.Выбрать из приведенных ниже такое значение в, чтобы график функции у=-10х+в проходил через точку А (2;-10)

а) -98; б) 10; в) -10

5.Чему равна длина отрезка, отсекаемого на оси ОУ прямой у = +3 ?

а) -3; б)3.

Тестирование позволяет измерять результаты обучения с большой долей объективности. Тесты имеют целый ряд положительных характеристик, позволяющих:

1) учитывать индивидуальные особенности учащихся в ходе проверки результатов обучения;

2) проверять качество усвоения учащимися теоретического и практического материала;

3) оживить процесс обучения, вводя не только новую для учащихся форму контроля, но и различные виды тестов;

4) сэкономить учебное время, затрачиваемое на опрос и личное время учителя, идущее на проверку результатов выполненной учащимися работы;

5) использовать тесты для компьютеризации;

6) обеспечить оперативность проверки выполненной работы.

Основные признаки отличия тестов школьной успеваемости, например, от контрольной работы, состоят в том, что с их помощью можно:

а) проверить большой объем изученного материала малыми порциями;

б) быстро диагностировать овладение учебным материалом большим массивом учащихся.

Однако метод тестирования обладает рядом недостатков:

б) проверка лишь результатов действий, затруднение со стороны учителя, а чаще невозможность проследить логику рассуждений учащихся;

в) категоричность оценки выполнения задания, ибо тесты учитывают только 2 состояния выполнения задания – задание выполнено правильно и полностью и задание не выполнено.

Существует несколько классификаций тестов в зависимости от выбранного основания.

Первый вид тестов предполагает заполнение пропусков в истинных утверждениях или в правильных формулировках математических определений, правил.

Второй вид требует установления истинности или ложности утверждений или правильности формулировок определений, теорем.

Третий вид предполагает выбор ответа из целого ряда вариантов, из которых только один верный. В тестах такого вида предполагается не менее трех ответов для выбора. При составлении ответов учитываются типичные ошибки учащихся.

К тестированию отношусь особенно внимательно – придя из начальной школы не все дети умеют работать с тестами, а к 10 – 11 классу они должны в совершенстве обладать этими навыками, ведь многим из них предстоит сдавать экзамен в форме ЕГЭ.

Среди методов проверки (способов изучения качества знаний, умений и навыков учащихся) выделяют устную проверку, проверку письменно-графических работ и проверку практических работ.

Важное место занимает проведение практических работ. Так можно проверить не только знания и соответствующие умения и навыки, но и умения и навыки пользования приборами, таблицами, инструментами и другими средствами. Практические работы провожу обзорные по пройденной теме, некоторые работы направлены на закрепление новых знаний и выработку практических навыков, третьи предшествуют изучению нового материала. Практические работы могут занимать от 10 до 30 минут урока, в зависимости от их цели и места в общей теме. Они подразделяются на тренировочные, обучающие, контролирующие и измерительные работы на местности. Все работы проверяю, но оцениваю по- разному: по результатам обзорных работ оценки выставляются в журнал, по результатам тренировочных работ иногда выставляю лишь положительные отметки, а результаты работ подготовительного характера иногда тоже просто рецензирую. При этом отмечаю точность и тщательность выполнения задания и проявленную при этом активность учащихся.

Иногда практической работе предшествует домашнее задание. Например, предлагаю дома вырезать из бумаги любой треугольник, измерить его стороны и углы, записать эти данные на отдельном листе. Лист и модель треугольника принести на урок. Проверку результатов практической работы можно организовать в форме взаимного рецензирования. Сюда же можно отнести и изготовление бумажных моделей многогранников, для дальнейшего нахождения их объёма или площади поверхности. Устную проверку организую по - разному в зависимости от ее целей и от содержания учебного материала; ее приемы различных этапах урока.

Итоговое оценивание учащегося (за четверть, полугодие, год) в условиях уровневой дифференциации непосредственно зависит от результатов сдачи зачётов. А именно, положительная итоговая оценка выставляется в том случае, если все зачёты за этот период им сданы.

Технология уровневой дифференциации имеет много преимуществ. Отношение учащихся изменилось, но не столько к предмету, сколько к оценке знаний. Учащиеся поняли, что даже оценка «зачёт» так просто не даётся.

Принцип «открытости» избавляет от вопросов: «А почему у мены 27», т.к. учащимся известно, с какими заданиями нужно справиться для получения той или иной оценки.

Зачёты показали, что данная работа помогает ученикам не только правильно оценивать свои знания, но и вовремя ликвидировать свои пробелы. У слабых появляется уверенность в собственных силах. Этому способствует посильность требований, и возможность повторно ответить материал, который не сразу был усвоен. Относиться к учёбе стали серьёзнее все.


Немаловажную роль я отвожу дидактическим играм - современному и признанному методу обучения и воспитания, обладающему образовательной, развивающей и воспитывающей функциями.

Например, использую дидактическую игру «Математический поединок». Основой ее является соревнование между командами при ответах на вопросы и решении упражнений, предложенных учителем. Такое название игры выбрано потому, что на равных условиях соревнуются 2 команды. При этом очень важно сохранение интереса школьников к игре. Дидактическая цель игры – проверка ранее полученных знаний. Широко использую проведение математических лабиринтов не только в старших классах, но и в 5-6.

Информацию об усвоении материала можно получить с помощью сигнальных карточек: красная, зеленая. Например, при устном опросе: если ученик за партой согласен с отвечающим, то он поднимает зеленую карточку, а если нет – красную. Таким образом, каждый ученик имеет возможность высказаться.

При проверке знаний можно использовать игру «Математическое лото». Правила игры: к уроку готовлю 5 больших карточек и соответствующее количество маленьких карточек с примерами.

0.5	0,05	0,25
0,3	4	2500
0,4	250	0,04

Большую карточку даю группам играющих. Вынимаю карточку, читаю пример (условия примеров можно проецировать на доску). Та группа, которая обнаруживает на большой карточке ответ и считает его правильным, забирает карточку у ведущего и накрывает ею соответствующую клеточку. Выигрывает та группа, которая раньше всех накрыла все клетки своих карт.




Упражнения к уроку «Деление на десятичную дробь» в 5 классе.

1. 
   0,8 : 0.2
   
2. 0,08 : 0,2
   
3. 250:0,5
   
4. 2,5 : 5
   
5. 2.5 : 0,01
   
6. 2,5 : 10
   
7. Решить уравнение: 3х=0,9
   
8. 5х=0,25
   

9 4х =0,16


Я считаю, что проверять качество домашней работы надо обязательно, а формы проверки могут быть разные.

Если на дом было задано осмысление и запоминание важного теоретического материала (правила, теоремы), то использую индивидуальную форму опроса. По большим темам каждый год провожу урок - панораму, урок – путешествие, уроки – семинары.

Вторым широко применяемым в обучении математике методом проверки является проверка письменно - графических работ, Этот метод служит тем же целям, что и метод устной проверки, но и имеет свои качественные особенности. Это большая объективность по сравнению с устной проверкой, охват нужного числа проверяемых, экономия времени.

Дидактические возможности метода письменной проверки очень велики. Именно с помощью письменных работ можно наиболее полно проверить умения применять правила, теоремы, свойства к решению задач, решение уравнений и неравенств, нахождение производных, вычисление интегралов, сформированность навыков, овладение приемами учебной работы.

По своему дидактическому назначению самостоятельные работы бывают обучающие и контролирующие. Смысл контролирующих самостоятельных работ заключается в самостоятельном выполнении учащимися данных учителем заданий после, как правило, логически завершенных порций учебного материала и констатирования на базе этого широты и глубины полученных учащимися знаний и умений. Самостоятельные работы являются одним из важнейших средств проверки систематического и прочного усвоения программного материала. Вместе с тем они служат формированию у учащихся интереса к предмету, воспитанию положительного отношения к учению.

Положительные эмоции учащихся на уроке – это залог успеха в обучении. Приобретение эмоционального опыта предусматривает определенные переживания, волевые усилия, что возможно лишь при активной мыслительной деятельности учащихся. Добиться перечисленного можно, в частности, с помощью такой нетрадиционной формы урока, как «Математический лабиринт». На этом уроке даже самые неактивные включаются в работу с огромным желанием, стараясь показать свои знания и умения, чтобы не подвести одноклассников. Ученики увлечены, переживают неудачи своей команды и радуются ее успеху. Во время прохождения «Математического лабиринта» школьники очень внимательны, сосредоточены и дисциплинированны, так как, чтобы победить, необходимо четко запомнить правила соревнования, за короткое время ответить на поставленные вопросы

Увеличена умственная нагрузка на уроках математики, пропадает интерес к учению у большинства учащихся. Задумываешься над тем, как поддержать у учащихся интерес к изучаемому материалу, их активность. Традиционные формы проверки знаний учащихся по математике желательно дополнять чем – то новым. Поэтому я, как и все учителя математики, буду искать новые методические приемы, которые призваны содействовать не только выявлению знаний, но и стимулировали бы учащихся к приобретению знаний.

В настоящее время созданы и распространяются такие средства, которые не требуют больших затрат времени на обработку результатов. Контрольно – обучающие устройства предоставляют ученикам возможность проконтролировать правильность выполненных им операций.

Современное школьное образование должно обеспечить достаточный уровень взаимодействия человека с компьютером. И перед нами, всеми учителями, стоит задача – в своей работе при проверке знаний учащихся соединять традиционные приемы и новые информационные технологии.

Есть ещё один момент, на котором я хотела бы остановиться отдельно. Это использование экологического компонента на уроках математики. Так как в условиях малокомплектной сельской школы экологическое направление в воспитательной деятельности является одним из приоритетных, наиболее близких сельским школьникам, понимаемых и принимаемых, возникает необходимость экологизации предметных курсов.


Слово «экология» прочно вошло в обиход. Произошло это не случайно. Современное человечество, вооруженное техникой и использующее огромное количество энергии, представляет очень мощную силу, воздействующую на природу Земли. Если эти воздействия не учитывают природных законов и разрушают установившиеся за миллионы лет связи, возникают катастрофические последствия. Люди уже столкнулись с целым рядом катастроф, вызванных их деятельностью, и обеспокоены тенденцией нарастания неустойчивости природы.

Поэтому экология в настоящее время приобретает особое значение как наука, помогающая найти пути выхода из возникающего кризиса. Раскрывая законы связей, на которых основана устойчивость жизни, люди всё глубже понимают, как нужно изменить и организовать свои собственные отношения с природной средой.

Воспитывать экологически грамотных людей - одна из главных задач современной школы.

Экологическое воспитание необходимо рассматривать как непрерывный и систематический процесс в течение всего периода школьного обучения. Такую возможность даёт экологизация школьных предметных курсов. На уроках можно заложить принципы, дающие основу понимания единства человека и окружающего мира, донести до каждого ребёнка чувство понимания и ответственности, лежащей перед человеком за изменения окружающего мира.


Математика является одним из предметов, который пока недостаточно связан с процессом экологизации, а между тем эти науки тесно переплетаются. Экологизация математики даёт нам возможность проследить процесс развития человеческих знаний во времени и пространстве.

Главная проблема в том, что пред учителем математики в настоящее время не стоит задача воспитания экологически грамотного ученика. Участию математики в процессе формирования экологического мировоззрения отводится одно из последних мест.

На уроках математики фактический материал по экологии может осознаваться и усваиваться в процессе решения задач. Отсюда вытекает вторая проблема экологизации математики: отсутствие пособий и задачников, включающих в себя задачи с экологической направленностью. Решение этой проблемы зависит пока от учителя, от его инициативы, творчества и сотрудничества с учителем экологии. Экологизация математики, в том числе математических задач будет способствовать получению учащимися знаний об окружающем мире и его экологических проблемах. Тематика задач может быть самой разнообразной: биологическая, геоэкологическая, социологическая, в том числе решение задач по проблеме природопользования, историческая, антропоэкологическая.

В связи с этим мною разработана программа изучения вопросов экологии вначале на занятиях математического кружка в 6 классе в 2007 – 2008 учебном году. В настоящее время работаю над составлением экологического компонента программы изучения курса алгебры в 7 классе.

Цель изучения курса алгебры в 7 классе - развитие вычислительных и формально-оперативных алгебраических умений учащихся до уровня, позволяющего уверенно их использовать при решении задач математики и смежных предметов, в том числе экологии. Прикладная направленность курса обеспечивается систематическим обращениям к примерам, раскрывающим возможности применения математики к изучению взаимодействий человека с окружающей средой и решения практических задач экологической направленности.

Математика создаёт условия для развития умения давать количественную оценку состояния природных объектов и явлений, положительных и отрицательных последствий деятельности человека в природном и социальном окружении. Текстовые задачи дают возможность для раскрытия вопросов о среде обитания, заботы о ней, рациональном природопользовании, восстановлении и приумножении её природных богатств.