М. В. Ломоносова Социологический факультет кафедра Информатики социальных процессов А. И. Самыловский Учебно-методический комплекс
| Вид материала | Учебно-методический комплекс |
- М. В. Ломоносова Социологический факультет кафедра Информатики социальных процессов, 1105.13kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 691.69kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 1668.25kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 663.83kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии безопасности, образования, 809.07kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 586.95kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии безопасности Викторов, 762.25kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии коммуникативных систем, 378.58kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 837.3kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 3044.39kb.
IX. Контрольные теоретические вопросы по учебным дисциплинам для итогового контроля знаний
Ориентировочные вопросы к зачету
по «Теории измерений»
(весенняя зачетная сессия на втором курсе)
-
Метод знаков, метод серий, метод Манна – Уитни (Уилкоксона) в социологических исследованиях.
Экспертное оценивание в социологических исследованиях.
-
Коэффициент конкордации в социологических исследованиях.
Основные типы шкал и их использование в социологических исследованиях.
Шкалирование латентных параметров и измерение их характеристик в социологических исследованиях.
-
Модели и методы сравнительного шкалирования, их достоинства и недостатки.
Метод попарных сравнений.
Шкалирование по Гуттману.
Q-сортировка.
Шкалирование по Тёрстоуну.
Модели и методы несравнительного шкалирования, их достоинства и недостатки.
-
Шкала Лайкерта.
Шкала семантического дифференциала.
Шкала Стэпела.
Визуализация результатов многомерного шкалирования и карты восприятия.
Понятия надежности и валидности измерительных инструментов в социологии.
-
Виды и методы исследования надежности.
Виды и методы исследования валидности.
Ориентировочные вопросы к зачету
по «Анализу данных»
(зимняя зачетная сессия на третьем курсе)
- Таблицы сопряженности и меры связи признаков.
- Сравнительный анализ различных мер связи в таблицах сопряженности.
- Модель дисперсионного анализа в анализе данных социологического исследования.
- Модель латинского квадрата в планировании социологического исследования.
- Модель регрессионного анализа в анализе данных социологического исследования.
- Модель номинального регрессионного анализа при проведении социологического исследования.
- Оценивание качества регрессионной модели при проведении социологического исследования.
- Использование понятий полной, множественной, частной корреляции при интерпретации данных социологического исследования.
- Модель главных компонентов в анализе данных социологического исследования.
- Модель факторного анализа в анализе данных социологического исследования.
- Интерпретация результатов факторного анализа с помощью атрибутивной карты восприятия.
- Модель канонических корреляций в анализе данных социологического исследования.
- Модель кластерного анализа данных социологического исследования.
- Модель дискриминантного анализа данных социологического исследования.
- Модель конджойнт-анализа данных социологического исследования.
- Модель пат-анализа данных социологического исследования.
- Модель лонгитюдного анализа данных социологического исследования.
- Модель контент-анализа данных социологического исследования.
X. Методические указания
Отдельные подразделы программы, содержащие стандартную тематику, могут выноситься на самостоятельную проработку (в рамках сетки часов самостоятельной работы по учебным дисциплинам) с последующей отчетностью студентов в виде рефератов по таким подразделам.
Для подготовки к контрольным работам студентам рекомендуется использовать, прежде всего, лекционные материалы и материалы семинарских занятий.
При выполнении домашних заданий (аналитических эссе) как по «Теории измерений», так и по «Анализу данных», рекомендуется использовать примеры анализа реальных социальных ситуаций (case-studies), в больших количествах содержащиеся, например, в книгах: п.п. 1 – 9 основной литературы. Там же приведены необходимые сведения о возможностях современных статистических пакетов и примеры их реального использования в социологических и маркетинговых исследованиях (прежде всего, сведения об опыте применения пакета SPSS).
Каждое домашнее задание (аналитическон эссе) выполняется строго на листах формата А4, которые скрепляются степлером (не скрепкой!). Допускается как рукописное, так и компьютерное выполнение и оформление, с использованием как одной, так и двух сторон листа. Каждое домашнее задание должно оформляться в виде самостоятельного документа со своим титульным листом (не следует, во избежание путаницы, объединять в одном документе, с единым титульным листом, несколько домашних заданий).
В целях текущего контроля работы студентов на каждой лекции в течение 5 – 7 минут проводится письменное тематическое тестирование (микро-контрольная работа) по материалу, как правило, предыдущих нескольких лекций. Такая работа каждым студентом выполняется строго на листе формата А5, надписывается (Ф.И.О., № группы, дата) и сдается лектору в лекционной аудитории в течение пяти минут после окончания лекции.
XI. Вспомогательные
вероятностно-статистические таблицы
Таблица 1. Биномиальная случайная величина Bi (n;p).
В таблице приведены значения биномиальных вероятностей (вероятностей для количества «успехов»
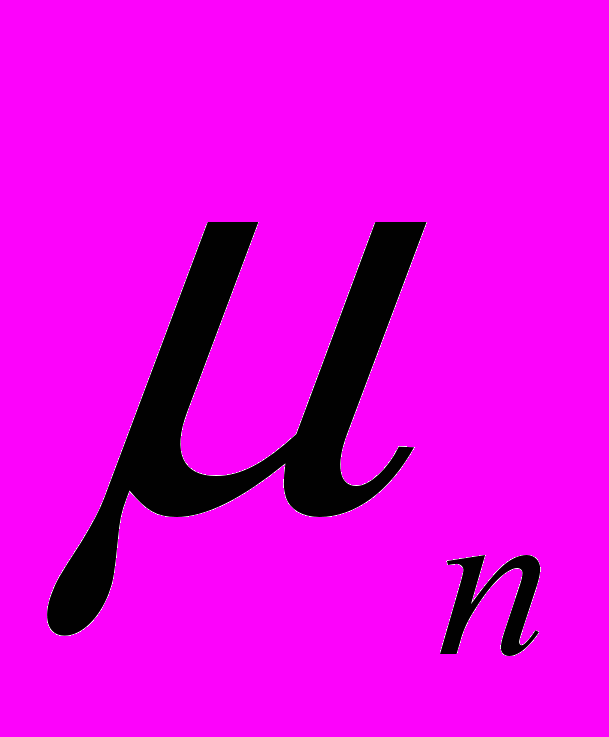в схеме Бернулли)
, k=0, 1, 2, …, n, при некоторых значениях количества испытаний n схемы Бернулли и вероятности «успеха» p в одном испытании (значения биномиальных вероятностей приведены с округлением до тысячных долей единицы). n=5
 pk | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| 0 | 0,590 | 0,328 | 0,168 | 0,078 | 0,031 |
| 1 | 0,328 | 0,410 | 0,360 | 0,259 | 0,156 |
| 2 | 0,073 | 0,205 | 0,309 | 0,346 | 0,313 |
| 3 | 0,008 | 0,051 | 0,132 | 0,230 | 0,313 |
| 4 | 0,000 | 0,006 | 0,028 | 0,077 | 0,156 |
| 5 | 0,000 | 0,000 | 0,002 | 0,010 | 0,031 |
n=10
 pk | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| 0 | 0,349 | 0,107 | 0,028 | 0,006 | 0,001 |
| 1 | 0,387 | 0,268 | 0,121 | 0,040 | 0,010 |
| 2 | 0,194 | 0,302 | 0,233 | 0,121 | 0,044 |
| 3 | 0,057 | 0,201 | 0,269 | 0,215 | 0,117 |
| 4 | 0,011 | 0,088 | 0,200 | 0,251 | 0,205 |
| 5 | 0,001 | 0,026 | 0,103 | 0,201 | 0,246 |
| 6 | 0,000 | 0,006 | 0,037 | 0,111 | 0,205 |
| 7 | 0,000 | 0,001 | 0,009 | 0,042 | 0,117 |
| 8 | 0,000 | 0,000 | 0,001 | 0,011 | 0,044 |
| 9 | 0,000 | 0,000 | 0,000 | 0,002 | 0,010 |
| 10 | 0,000 | 0,000 | 0,000 | 0,000 | 0,001 |
n=15
| p k | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| 0 | 0,206 | 0,035 | 0,005 | 0,000 | 0,000 |
| 1 | 0,343 | 0,132 | 0,031 | 0,005 | 0,000 |
| 2 | 0,267 | 0,231 | 0,092 | 0,022 | 0,003 |
| 3 | 0,129 | 0,250 | 0,170 | 0,063 | 0,014 |
| 4 | 0,043 | 0,188 | 0,219 | 0,127 | 0,042 |
| 5 | 0,010 | 0,103 | 0,206 | 0,186 | 0,092 |
| 6 | 0,002 | 0,043 | 0,147 | 0,207 | 0,153 |
| 7 | 0,000 | 0,014 | 0,081 | 0,177 | 0,196 |
| 8 | 0,000 | 0,003 | 0,035 | 0,118 | 0,196 |
| 9 | 0,000 | 0,001 | 0,012 | 0,061 | 0,153 |
| 10 | 0,000 | 0,000 | 0,003 | 0,024 | 0,092 |
| 11 | 0,000 | 0,000 | 0,001 | 0,007 | 0,042 |
| 12 | 0,000 | 0,000 | 0,000 | 0,002 | 0,014 |
| 13 | 0,000 | 0,000 | 0,000 | 0,000 | 0,003 |
| 14 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 15 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
n=20
| p k | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| 0 | 0,122 | 0,012 | 0,001 | 0,000 | 0,000 |
| 1 | 0,270 | 0,058 | 0,007 | 0,000 | 0,000 |
| 2 | 0,285 | 0,137 | 0,028 | 0,003 | 0,000 |
| 3 | 0,190 | 0,205 | 0,072 | 0,012 | 0,001 |
| 4 | 0,090 | 0,218 | 0,130 | 0,035 | 0,005 |
| 5 | 0,032 | 0,175 | 0,179 | 0,075 | 0,015 |
| 6 | 0,009 | 0,109 | 0,192 | 0,124 | 0,037 |
| 7 | 0,002 | 0,055 | 0,164 | 0,166 | 0,074 |
| 8 | 0,000 | 0,022 | 0,114 | 0,180 | 0,120 |
| 9 | 0,000 | 0,007 | 0,065 | 0,160 | 0,160 |
| 10 | 0,000 | 0,002 | 0,031 | 0,117 | 0,176 |
| 11 | 0,000 | 0,000 | 0,012 | 0,071 | 0,160 |
| 12 | 0,000 | 0,000 | 0,004 | 0,036 | 0,120 |
| 13 | 0,000 | 0,000 | 0,001 | 0,015 | 0,074 |
| 14 | 0,000 | 0,000 | 0,000 | 0,005 | 0,037 |
| 15 | 0,000 | 0,000 | 0,000 | 0,001 | 0,015 |
| 16 | 0,000 | 0,000 | 0,000 | 0,000 | 0,005 |
| 17 | 0,000 | 0,000 | 0,000 | 0,000 | 0,001 |
| 18 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 19 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 20 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
Таблица 2. Пуассоновская случайная величина Po (λ).
В таблице приведены значения пуассоновских вероятностей
при некоторых значениях параметра k (количество «успехов» в «длинной»: n→∞ схеме Бернулли с «редкими»: p→0 успехами) и параметра λ (λ=np), а также значения суммы вида 
при некоторых значениях параметров λ и m (значения пуассоновских вероятностей и их сумм приведены с округлением до сотых долей единицы). Значения величины
 λk | 0,5 | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 |
| 0 | 0,61 | 0,37 | 0,14 | 0,05 | 0,02 | 0,01 | 0,00 | 0,00 | 0,00 | 0,00 |
| 1 | 0,30 | 0,37 | 0,27 | 0,15 | 0,07 | 0,03 | 0,01 | 0,01 | 0,00 | 0,00 |
| 2 | 0,08 | 0,18 | 0,27 | 0,22 | 0,15 | 0,08 | 0,04 | 0,02 | 0,01 | 0,00 |
| 3 | 0,01 | 0,06 | 0,18 | 0,22 | 0,20 | 0,14 | 0,09 | 0,05 | 0,03 | 0,01 |
| 4 | 0,00 | 0,02 | 0,09 | 0,17 | 0,20 | 0,18 | 0,13 | 0,09 | 0,06 | 0,03 |
| 5 | 0,00 | 0,00 | 0,04 | 0,10 | 0,16 | 0,18 | 0,16 | 0,13 | 0,09 | 0,06 |
| 6 | 0,00 | 0,00 | 0,01 | 0,05 | 0,10 | 0,15 | 0,16 | 0,15 | 0,12 | 0,09 |
| 7 | 0,00 | 0,00 | 0,00 | 0,02 | 0,06 | 0,10 | 0,14 | 0,15 | 0,14 | 0,12 |
| 8 | 0,00 | 0,00 | 0,00 | 0,01 | 0,03 | 0,07 | 0,10 | 0,13 | 0,14 | 0,13 |
| 9 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,04 | 0,07 | 0,10 | 0,12 | 0,13 |
| 10 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,02 | 0,04 | 0,07 | 0,10 | 0,12 |
| 11 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,02 | 0,05 | 0,07 | 0,10 |
| 12 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,03 | 0,05 | 0,07 |
| 13 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,03 | 0,05 |
| 14 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,02 | 0,03 |
| 15 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,02 |
| 16 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 |
| 17 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 |
| 18 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
Значения величины
 λm | 0,5 | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 |
| 0 | 0,61 | 0,37 | 0,14 | 0,05 | 0,02 | 0,01 | 0,00 | 0,00 | 0,00 | 0,00 |
| 1 | 0,91 | 0,74 | 0,41 | 0,20 | 0,09 | 0,04 | 0,02 | 0,01 | 0,00 | 0,00 |
| 2 | 0,99 | 0,92 | 0,68 | 0,42 | 0,24 | 0,12 | 0,06 | 0,03 | 0,01 | 0,01 |
| 3 | 1,00 | 0,98 | 0,86 | 0,65 | 0,43 | 0,27 | 0,15 | 0,08 | 0,04 | 0,02 |
| 4 | 1,00 | 1,00 | 0,95 | 0,82 | 0,63 | 0,44 | 0,27 | 0,17 | 0,10 | 0,05 |
| 5 | 1,00 | 1,00 | 0,98 | 0,92 | 0,79 | 0,62 | 0,45 | 0,30 | 0,19 | 0,12 |
| 6 | 1,00 | 1,00 | 1,00 | 0,97 | 0,89 | 0,76 | 0,61 | 0,45 | 0,31 | 0,21 |
| 7 | 1,00 | 1,00 | 1,00 | 0,99 | 0,95 | 0,87 | 0,74 | 0,60 | 0,45 | 0,32 |
| 8 | 1,00 | 1,00 | 1,00 | 1,00 | 0,98 | 0,93 | 0,85 | 0,73 | 0,59 | 0,46 |
| 9 | 1,00 | 1,00 | 1,00 | 1,00 | 0,99 | 0,97 | 0,92 | 0,83 | 0,72 | 0,59 |
| 10 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,99 | 0,96 | 0,90 | 0,82 | 0,71 |
| 11 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,99 | 0,98 | 0,95 | 0,89 | 0,80 |
| 12 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,99 | 0,97 | 0,94 | 0,88 |
| 13 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,99 | 0,97 | 0,93 |
| 14 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,99 | 0,98 | 0,96 |
| 15 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,99 | 0,98 |
| 16 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,99 |
| 17 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,99 |
| 18 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
| 19 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |