В. Ф. Столяров, д-р екон наук, проф

Вид материала

Документы

Содержание 1.7.3. Теорія оптимізації портфеля інвестицій А — рівень ризику (показник квадратичного відхилення) інвестицій А В — 0,8. Очікувана рентабельність такого інвестиційного портфеля становитиме: r Головний висновок для фінансистів-практиків

Подобный материал:

• Міністерство України у справах сім’ї, молоді та спорту становище сімей в україні, 4532.43kb.
• Інформаційні технології в журналістиці: вітчизняний І світовий досвід Київ 2002, 8272.38kb.
• Міжнародна журналістика – 2002 київ 2002, 2743.9kb.
• Приглашение и программа разнообразие почв и биоты северной и центральной азии, 521.14kb.
• Научный выпуск вестник балтийской педагогической академии вып. 29. – 2000 г. Поиск, 1745.18kb.
• Удк 330. 101. 541(075. 8) Ббк 65. 012. 2я73, 1872.14kb.
• О. О. Метешкін, д-р техн наук, проф. Харківського військового університету; > Н. А., 2672.74kb.
• В. Г. Швець, д-р екон наук, проф, 4046.01kb.
• Дипломных проектов по специальностям, 283.96kb.
• Вестник балтийской педагогической академии вып. 94. – 2010 г. Актуальные проблемы нравственного, 2431.92kb.

1.7.3. Теорія оптимізації портфеля інвестицій

Одним з базових елементів сучасної теорії ринку капіталу є концепція оптимізації портфеля інвестицій. Автором її є американський економіст, лауреат Нобелівської премії з економіки Г. Марковіц. У 1952 р. він уперше обґрунтовано довів, що вкладення заданого обсягу інвестиційного капіталу в один об’єкт інвестицій є ризикованішим, ніж інвестування цієї ж суми в різні об’єкти (диверсифікація). Завдяки диверсифікації можна зменшити сукупний ризик портфеля інвестицій підприємства. Автор зробив спробу аргументувати правило формування портфеля інвестицій, тобто дати відповідь на питання щодо кількості і виду цінних паперів (об’єктів інвестицій), які повинні бути відібрані в інвестиційний портфель з погляду оптимізації співвідношення «ризик—прибутковість» за заданого обсягу інвестиційних ресурсів[18]. Далі висновки Марковіца щодо оптимізації портфеля цінних паперів були застосовані з метою формування портфеля реальних інвестицій підприємства.

За Марковіцем, портфель інвестицій вважатиметься оптимальним, якщо, з одного боку, за однакового рівня прибутковості не існуватиме будь яких-інших інвестиційних можливостей з меншим рівнем ризику; з іншого — не існуватиме інших, прибутковіших інвестиційних портфелів, які характеризуються таким самим рівнем ризику. При цьому йдеться про так звані несис­тематичні ризики.

Несистематичні ризики — це специфічні ризики, властиві конкретним активам, наприклад ризик отримання збитків від операційної діяльності, а отже, ризик падіння прибутковості фінансового активу тощо. Зазначені ризики можуть бути мі-
німізовані на основі широкої диверсифікації інвестиційного портфеля.

Логіку концепції можна простежити, дослідивши модель формування інвестиційного портфеля за рахунок двох фінансових активів (А та В), після чого одержані висновки можна спроектувати на інвестиційний портфель з великою кількістю цінних паперів. Згідно з припущенням, очікувана прибутковість портфеля інвестицій (r_p) може розраховуватися за формулою середньої арифметичної зваженої; вагами (a_i) при цьому виступають частки окремих фінансових активів у структурі інвестиційного портфеля:

, (1.1)

де n — число цінних паперів, які складають інвестиційний портфель; r_i — прибутковість і-го фінансового активу, питома вага якого в структурі портфеля становить а_і.

Рівень ризику портфеля інвестицій залежить від питомої ваги окремих цінних паперів, які до нього входять, та коефіцієнта кореляції між їх прибутковістю. В моделі з двома активами величина ризику (який вимірюється показником квадратичного (стандартного) відхилення) описується такою формулою:

, (1.2)

де а — питома вага інвестицій А в інвестиційному портфелі; s_р — рівень ризику портфеля інвестицій; s _А — рівень ризику (показник квадратичного відхилення) інвестицій А; s_В — рівень ризику (показник квадратичного відхилення) інвестицій В; K(r_A; r_B) — коефіцієнт кореляції, щільність зв’язку між рентабельністю активів А та В.

Ризиковість портфеля інвестицій, як правило, не дорівнює сумі ризиків окремих об’єктів, які складають інвестиційний портфель, чи середньому показнику їх ризиковості. Це можна спостерігати лише в тому разі, якщо прибутковість окремих об’єктів інвестицій повністю корелює між собою (перебуває у прямій функціональній залежності), тобто коефіцієнт кореляції складає + 1. Формулу 1.2, за умови, що K(r_A; r_B) = +1, можна подати у такому вигляді:

s_р = аs_А + (1 – а) s_В. (1.3)

За максимальної кореляції зменшити ризиковість інвестиційного портфеля через використання ефекту диверсифікації неможливо: інвестор може обирати будь-яку комбінацію цінних паперів. Можливі комбінації портфелів інвестицій, які складаються з А та В, лежать на прямій АВ (рис. 1.8).



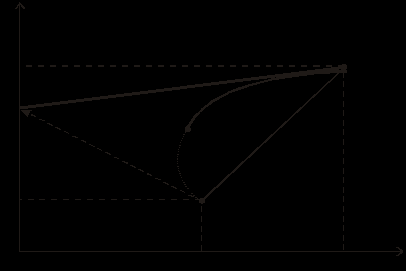
Рис. 1.8. Залежність ризику портфеля інвестицій
від коефіцієнта кореляції

Вважається, що в міру того, як позитивний кореляційний зв’язок між рентабельністю окремих активів зменшується, рівень ризику інвестиційного портфеля набуває меншого значення, ніж середня величина ризику окремих цінних паперів, за рахунок яких сформовано портфель.

У разі, якщо кореляційний зв’язок повністю зворотний (зворотна функціональна залежність) і коефіцієнт кореляції K (r_A; r_B) = –1, рівень ризику інвестиційного портфеля рекомендується визначати як:

s_р = аs_А – (1 – а) s_В. (1.4)

За повністю зворотного кореляційного зв’язку можна сформувати портфель інвестицій з нульовим рівнем ризику та позитивною рентабельністю. При цьому висока прибутковість одних активів компенсується низьким рівнем інших, і навпаки.

 

Приклад 1.1

Знайдемо співвідношення, з яким слід сформувати портфель інвестицій з двох видів цінних паперів А та В, за якого ризик портфеля інвестицій дорівнюватиме нулю. Коефіцієнт кореляції між їх рентабельністю дорівнює –1. Квадратичне відхилення за вказаними інвестиціями дорівнює, відповідно: s_А = 8; s_В = 2.

Підставивши відповідні значення у формулу 1.4, одержимо шукану питому вагу окремих інвестицій: 0 = а8 – (1 – а)2; звідси
а = 0,2. Таким чином, питома вага цінних паперів А у структурі
інвестиційного портфеля повинна дорівнювати 0,2, відповідно
В — 0,8. Очікувана рентабельність такого інвестиційного портфеля становитиме: r_p = 0,2r_А + 0,8r_В.

 

Можливі комбінації портфелів цінних паперів за умови, що коефіцієнт кореляції становить –1, на рис. 1.8 лежать на прямій GB.

У разі, якщо коефіцієнт кореляції дорівнює нулю, тобто кореляційний зв’язок повністю відсутній, можна знайти комбінації цінних паперів, за яких рентабельність інвестиційного портфеля зростатиме за спадного рівня ризику. Якщо ж коефіцієнт кореляції знаходиться між 0 та 1, інвестору рекомендується обирати комбінацію цінних паперів, яка міститься на кривій QB (рис. 1.8).

Проблематика використання моделі Марковіца в практичній фінансовій діяльності підприємств для підбирання оптимального портфеля інвестицій зумовлена такими чинниками:

модель не враховує фактору часу, зокрема вона дає відповідь на питання щодо кількості та виду цінних паперів, за рахунок яких слід формувати інвестиційний портфель, однак ігнорує питання найбільш оптимального часу придбання та продажу активів;

складність збору інформації та статистичних розрахунків, на яких ґрунтуються інвестиційні рішення;

неврахування методології фундаментального і технічного ана­лізу акцій.

Головний висновок для фінансистів-практиків, який випливає з концепції Марковіца, полягає в тому, що в рамках стратегії мінімізації інвестиційних ризиків слід підбирати такий портфель інвестицій, в якому пріоритет віддається не стільки цінним паперам, рівень ризику кожного з яких є мінімальним, скільки комбінації активів з мінімальним кореляційним зв’язком між рівнями їх рентабельності. Така стратегія є прагматичнішою, ніж вибір найбільш прибуткових чи найменш ризикових фінансових активів. Причому за заданого рівня прибутковості ризик буде тим меншим, чим диверсифікованішим є інве­стиційний портфель.