Курс «управление проектами» Авторы: Сооляттэ Андрей Юрьевич (Раздел I) Шулимов Андрей Владимирович (Раздел II) Кац Анна Борисовна (Раздел III)

Вид материала

Документы

Содержание 2.4. Точка безубыточности 2.5. Метод Монте-Карло. Ожидаемые потери инвестора П — Стоимость неопределенности Коэффициент ожидаемых потерь

Подобный материал:

• Курс «управление проектами» Авторы: Сооляттэ Андрей Юрьевич (Раздел I) Шулимов Андрей, 6710.07kb.
• Эмоциональное и познавательное развитие ребенка на музыкальных занятиях, 456.98kb.
• С изменениями от 31 декабря 2002 г Приказом гугпс, 1150.26kb.
• Учебно-методический комплекс дисциплины «физическая культура» Смоленск 2006, 3244.71kb.
• Учебное пособие Для студентов вузов в 2-х частях, 2621.7kb.
• Основные категории политической науки (Раздел учебного пособия), 334.4kb.
• Программно-целевое планирование 42 > Транспорт и дорожное хозяйство 43 > 10. Жилищно-коммунальное, 1382.7kb.
• Кп «Одеспроект» Лицензия ав №555509, 253.51kb.
• Дмитриев Владимир Александрович. Организационно-методические указания, 147.06kb.
• Программа курса история западноевропейской философии раздел III. Философия Возрождения., 197.54kb.

2.4. Точка безубыточности

Одним из наиболее важных показателей является точка безубыточности, характеризующая объем про­даж, при котором выручка от реализа­ции продукции совпадает с издержками производства.

При определении этого показателя принимается, что издержки на производство продукции могут быть разделены на условно-по­стоянные (не изменяющиеся при изменении объема производства) издержки Зс и условно-переменные, изменяющиеся прямо пропор­ционально объему производства 3v (объем). Точка безубыточности (Q) определяется по формуле:

Q=3c/(Ц-3v),

где Ц— цена единицы продукции.

Под точкой безубыточности понимают такое состояние, когда разность между всеми расходами и доходами равна 0, то есть совокупные текущие расходы (Р) равны совокупным доходам от реализации проекта (Д).

Д = Р

Доходы от реализации проекта представляют собой доходы от продажи товаров (работ, услуг) и определяются произведением количества единиц продукции (К) на цену за единицу (Ц).

Д = К * Ц

Совокупные текущие расходы состоят из условно-постоянной и составляющих:

Р = Зс + Зv * К

где Зс - условно-постоянные (фиксированные) издержки,

Зv - условно-переменные издержки на единицу продукции.

Условно-постоянные издержки – это издержки, которые зависят от изменения объема выпуска продукции. К ним относятся амортизация здания, производственного оборудования, содержания транспорта, проценты на капитал, заработная плата управленческого персонала, аренда установок и помещения, страхование, коммунальные услуги и т.п.

Условно-переменными издержками называют издержки, которые изменяются в зависимости от объема выпуска продукции. К ним относятся: сырье, материалы, заработная плата производственных рабочих, топливо, торговые издержки и др.

Итак равенство Д = Р можно записать в виде:

Ц*К = Зс + Зv * К

Количество единиц реализованной продукции, необходимое для достижения точки безубыточности, будет равно:

Q = Зс/ (Ц - Зv)

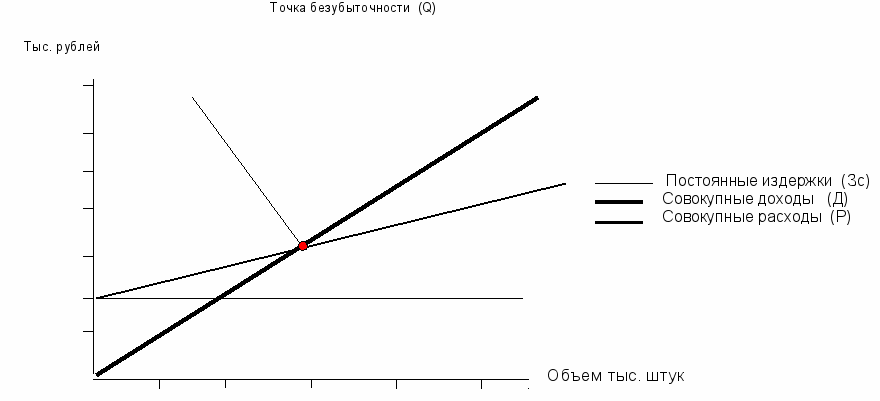
Для подтверждения работоспособности проектируемого производства (на данном шаге расчета) необходимо, чтобы значение точки безубыточности было меньше значений номинальных объемов производства и продаж (на этом шаге). Чем дальше от них значение точки безубыточности (в процентном отношении), тем устойчивее проект. Графическое представление точки безубыточности приведено на рисунке.


350


300


250


200





150


100


50


0


0 10 20 30 40 50


Рис. 2 Графическое представление точки безубыточности

2.5. Метод Монте-Карло.

Методом формализованного Описания неопределенности, используемый в сложных для прогнозирования проектах, является метод Монте-Карло. Он основан на применении имитационных моделей, позволяющих создавать множество сценариев, которые согласуются с заданными ограничениями на исходные переменные.

Метод Монте-Карло наиболее полно отражает всю гамму неопределенностей, с которой может столкнуться реальный проект, но в то же время, через начально-заданные ограничения учитывает всю информацию, имеющуюся в распоряжении аналитика проекта.

На практике данный метод может быть осуществлен только с применением компьютерных программ, позволяющих описывать прогнозные модели и рас­считывать большое число случайных сценариев. При применении метода не­обходимо учитывать, что точность результатов во многом определяется тем, насколько хороша созданная прогнозная модель.

Последовательность действий при реализации этого метода должна быть следующей:

1. Создание прогнозной модели. В качестве прогнозной модели выступают математические зависимости, полученные при расчете показателей экономи­ческой эффективности, обычно — ЧДД.
   
2. Выявление ключевых факторов, то есть переменных, которые в значи­тельной степени влияют на результаты проекта (на этом этапе используются результаты анализа чувствительности) и имеют значительную вероятность на­ступления.
   
3. Определение распределения вероятности ключевых факторов. Для этого:
   

• устанавливаются минимальное и максимальное значения, которые, по мнению аналитика, могут принять ключевые факторы;
  
• прогнозируются вид и параметры распределения вероятности внутри за­данных границ.
  

4. Выявление корреляционных зависимостей между переменными. Долж­ны быть выявлены все зависимые переменные и по возможности точно (с помощью коэффициентов корреляции) описана степень этих зависимостей. Иначе созданная модель может привести к заведомо неверным выводам.
   
5. Генерирование множества случайных сценариев, основанных на задан­ных ограничениях. Для реализации этого этапа требуется описание прогноз­ной модели на компьютере. Количество "прогонов" модели, выполняемой на компьютере, должно быть достаточно, чтобы полученная выборка была реп­резентативна.
   
6. Статистический анализ результатов имитационного моделирования. Ос­новным критерием принятия решения с учетом статистического анализа риска является следующий: следует выбирать проект с таким распределением ве­роятности ЧДД, которое наилучшим образом соответствует отношению к рис­ку конкретного инвестора. Помимо вероятностных характеристик ЧДД (мате­матического ожидания, среднеквадратического отклонения и коэффициента вариации), при реализации данного метода могут быть определены следую­щие показатели:
   

Ожидаемые потери инвестора П — сумма всех отрицательных результа­тов, помноженных на вероятность их наступления.

Ожидаемые доходы от проекта Д — сумма всех положительных резуль­татов, помноженных на вероятность их наступления.

Для инвестора может быть определена Стоимость неопределенности, равная П, если проект будет принят, и Д, если проект будет отвергнут. Это понятие можно использовать для определения целесообразности поиска даль­нейшей уточняющей информации о проекте.

Коэффициент ожидаемых потерь К=П/(П+Д). Этот показатель можно использовать, для оценки уровня риска проекта, имеющего вероятность полу­чения как положительных, так и отрицательных результатов.