Стратегическое адаптивное планирование 26 Реализация маи в Excel 32 Реализация маи в MathCad 38
| Вид материала | Лекция |
- Департамент образования города Москвы Северное окружное управление образования гоу, 18.79kb.
- Оптимальний розподіл однорідних ресурсів із використанням Mathcad І Excel. Мета, 61.72kb.
- В г. Алушта на базе отдыха маи состоится научно-технический семинар, 60.93kb.
- Использование Mathcad и Excel при изучении школьного курса физики, 67.71kb.
- «Реализация метода оптимизация функции нескольких переменных (метод покоординатного, 58.58kb.
- Волгоградский филиал, 1123.83kb.
- Тематика курсовых работ по линейной алгебре Матрицы и определители: реализация основных, 8.06kb.
- Планирование стратегическое, 69.11kb.
- Программа конструирование и реализация модели культурологической школы Авторы программы:, 613.85kb.
- Концепция развития нанотехнологий в инновационном обществе, 206.69kb.
Парное сравнение компонент иерархии
Опишем метод парных сравнений (точнее модификацию по Т. Саати).
В данной модификации, как и в классическом варианте метода парных сравнений, производится сравнение изучаемых факторов между собой. Причем в данном методе факторы сравниваются попарно по отношению к их воздействию («весу», или «интенсивности») на общую для них характеристику.
Пусть в конкретной задаче необходимо определить состав некоторого объекта. Причем пусть A1, A2, ...,An основные факторы, определяющие состав объекта. Тогда для определения структуры объекта заполняется матрица парных сравнений.
| | A1 | A2 | ... | An |
| A1 | 1 | a12 | | a1n |
| A2 | a21 | 1 | | a2n |
| ... | | | ... | |
| An | an1 | an2 | | 1 |
Если обозначить долю фактора Ai через wi, то элемент матрицы aij= wi/ wj.
Таким образом, в предлагаемом варианте применения метода парных сравнений, определяются не величины разностей значений факторов, а их отношение. При этом очевидно aij= 1/aji. Следовательно, матрица парных сравнений в данном случае является положительно определенной, обратносимметричной матрицей, имеющей ранг равный 1.
Работа экспертов состоит в том, что, производя попарное сравнение факторов A1, ...,An эксперт заполняет таблицу парных сравнений. Важно понять, что если w1, w2, ..., wn неизвестны заранее, то попарные сравнения элементов производятся с использованием субъективных суждений, численно оцениваемых по шкале, а затем решается проблема нахождения компонента w.
В подобной постановке задачи решение проблемы состоит в отыскании вектора (w1, w2, ..., wn). Существует несколько различных способов вычисления искомого вектора. Каждый из методов позволяет кроме непосредственного нахождения вектора отвечать еще на некоторые дополнительные вопросы. Подробнее об этом будет написано ниже.
Подчеркнем, что эксперт сравнивая n факторов реально проводит не n (как это происходит при заполнении обычных анкет) сравнений, а n*(n-1)/2 сравнений. Но это еще не все. На самом деле (учитывая соотношение aij=aiк* aкj справедливое для всех значений индекса k) производится опосредованное сравнение факторов Ai и Aj через соответствующие сравнения этих факторов с фактором Ak. Принимая во внимание сделанное замечание можно утверждать, что в действительности эксперт производит значительно больше сравнений, чем даже показывает первая оценка равная n*(n-1)/2. Таким образом, каждая клетка матрицы парных сравнений реально содержит не одно число (результат непосредственного сравнения), а целый вектор (с учетом всех опосредованных сравнений через сравнения с другими факторами). Учет этих дополнительных сравнений позволяет значительно повысить надежность получаемых результатов, или позволяет значительно уменьшить количество необходимых экспертов.
Один из основных методов отыскания вектора w основывается на одном из утверждений линейной алгебры.
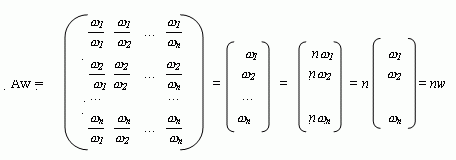
Очевидно, что искомый вектор является собственным вектором матрицы парных сравнений, соответствующим максимальному собственному числу (max). В этом случае по одному из большого количества существующих алгоритмов отыскивается max, а затем достаточно решить векторное уравнение A*w=max*w.
Здесь необходимо отметить следующее. Из линейной алгебры известно, что у положительно определенной, обратносимметричной матрицы, имеющей ранг равный 1, максимальное собственное число равно размерности этой матрицы (т.е. n). При проведении сравнений в реальной ситуации вычисленное максимальное собственное число max будет отличаться от соответствующего собственного числа для идеальной матрицы. Это различие характеризует так называемую рассогласованность реальной матрицы. И, соответственно, характеризует уровень доверия к полученным результатам. Чем больше это отличие, тем меньше доверие. Таким образом, эта модификация метода парных сравнений содержит внутренние инструменты позволяющие определить качество обрабатываемых данных и степень доверия к ним. Эта особенность данной методики выгодно отличает его от большинства обычно применяемых при исследовании рынка методов.
Шкала относительной важности
Другой подход в определении вектора w состоит в следующем. Суммируются по строкам элементы матрицы парных сравнений (для каждого значения i вычисляется сумма ai=ai1+ ai2+...+ ain). Затем все ai нормируются так, чтобы их сумма была равна 1. В результате получаем искомый вектор w. Таким образом
wi=ai/(a1+a2+...+an).
Для проведения субъективных парных сравнений Т. Саати была разработана шкала относительной важности.
Шкала относительной важности
| Интенсивность относительной важности | Определение | Объяснение |
| 0 | Несравнимы | Эксперт затрудняется в сравнении |
| 1 | Равная важность | Равный вклад двух видов деятельности в цель |
| 3 | Умеренное превосходство одного над другим | Опыт и суждения дают легкое превосходство одному виду деятельности над другим |
| 5 | Существенное или сильное превосходство | Опыт и суждения дают сильное превосходство одному виду деятельности над другим |
| 7 | Значительное превосходство | Одному из видов деятельности дается настолько сильное превосходство, что оно становится практически значительным |
| 9 | Очень сильное превосходство | Очевидность превосходства одного вида деятельности над другим подтверждается наиболее сильно |
| 2,4,6,8 | Промежуточные решения между двумя соседними суждениями | Применяются в компромиссном случае |
| Обратные величины приведенных выше чисел | Если при сравнении одного вида деятельности с др. получено одно из вышеуказанных чисел (3), то при сравнении второго вида деятельности с первым получим обратную величину (т.е. 1/3) | |
Выбор шкалы определялся следующими требованиями:
(а) Шкала должна давать возможность улавливать разницу в чувствах людей, когда они проводят сравнения, различать как можно больше оттенков чувств, которые имеют люди.
(б) Эксперт должен быть уверенным во всех градациях своих суждений одновременно.
Как показывают работы автора Т. Саати по сравнению этой шкалы с 28 другими шкалами, предложенными разными лицами, эта шкала и ее незначительные модификации лучше, чем все другие шкалы.
Опыт показал, что при проведении попарных сравнений в основном ставятся следующие вопросы. При сравнении элементов А и Б:
- Какой из них важнее или имеет большее воздействие ?
- Какой из них более вероятен ?
- Какой из них предпочтительнее ?
Относительная сила, величина или вероятность каждого отдельного объекта в иерархии определяется оценкой соответствующего ему элемента собственного вектора матрицы приоритетов, нормализованного к единице. Процедура определения собственных векторов матриц поддается приближению с помощью вычисления геометрической средней.
Пусть:
A1...An - множество из n элементов;
W1...Wn - соотносятся следующим образом:
 |  A1 |  ... |  An |
| A1 | 1 | ... | W1/Wn |
| ... | ... | 1 | An |
| An | Wn/W1 | ... | 1 |
Оценка компонент вектора приоритетов производится по схеме:
 |  A1 |  ... |  An | | |
| A1 | 1 | ... | W1/Wn | X1=(1*(W1/W2)*...*(W1/Wn))1/n | BEC(A1)=X1/СУММА(Xi) |
| ... | ... | 1 | An | ... | ... |
| An | Wn/W1 | ... | 1 | Xn=((Wn/W1)*...*(Wn/Wn-1)*1)1/n | BEC(An)=Xn/СУММА(Xi) |
| | СУММА(Xi) | | |||
Приоритеты синтезируются начиная со второго уровня вниз. Локальные приоритеты перемножаются на приоритет соответствующего критерия на вышестоящем уровне и суммируются по каждому элементу в соответствии с критериями, на которые воздействует элемент.
Весьма полезным побочным продуктом теории является так называемый индекс согласованности (ИС), который дает информацию о степени нарушения согласованности. Вместе с матрицей парных сравнений мы имеем меру оценки степени отклонения от согласованности. Если такие отклонения превышают установленные пределы, то тому, кто проводит суждения, следует перепроверить их в матрице.
ИС = ( max - n)/(n - 1)
Рассмотрим структуру метода более подробно на примерах:
Идеальные измерения
Пусть нам предложено сравнить веса предметов S1, …, Sn.
Рассмотрим идеальную ситуацию, предположив, что в нашем распоряжении их идеально точные веса. Обозначим эти веса через
wwn
соответственно.
Отношение
aik=wi/wk,i,k=1,…,n, (1.1)
показывает, во сколько раз вес i-го камешка Si, больше веса k-го камешка Sk.
Например, если w = 305 г и w = 244 г, то отношение
w / w = 305 / 244 = 1,25
говорит о том, что камешек S1 в 1,25 раза тяжелее камешка S2.
Запишем отношения (1.1) в виде квадратной матрицы
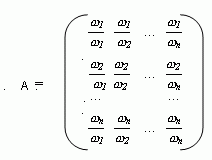
и проанализируем некоторые свойства этой идеальной матрицы сравнений.
1. Для любого i справедливо равенство aii = 1 (элемент матрицы А, расположенный на пересечении i-й строки и i-го столбца, равен единице).
В самом деле,
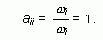
2. Для любых i и справедливо равенство
aki = 1 / aik (произведение элемента матрицы А, расположенного на пересечении i-й строки и k-го столбца на элемент матрицы А, расположенный на пересечении k-й строки и i-го столбца, равно единице).
В самом деле, из того, что
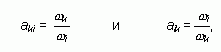
следует равенство
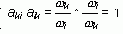
3. Для любых i, k и l справедливо равенство aik akl = ail (произведение элемента матрицы А, расположенного в i-й строке и k-м столбце, на элемент матрицы А, расположенный в k-й строке и l-м столбце, равно элементу матрицы А, расположенному в i-й строке и l-м столбце).
В самом деле,
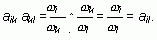
4. Столбец
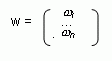
является собственным столбцом матрицы А с собственным значением l = n.
В самом деле,
Обратно-симметричные и согласованные матрицы
Рассмотрим теперь квадратную положительную матрицу порядка n:

a11 … a1k … a1n
………………
А = ai1 … aik … ain
………………
an1 … ank … ann
Матрица А называется обратно-симметричной, если для любых i и k выполняется соотношение:
aki = 1 / aik..
Из этого, в частности, следует, что
aii = 1.
Матрица А называется согласованной, если для любых i, k и l имеет место равенство aik akl = ail.
Тем самым, идеальная матрица сравнений – обратно-симметричная и согласованная.
Справедливо следующее утверждение.
ТЕОРЕМА. Положительная обратно-симметричная матрица является согласованной тогда и только тогда, когда порядок матрицы и ее наибольшее собственное значение совпадают:
lmax = n.
Шкалирование
Почему выбираются числа от 1 до 9?
Вот только некоторые из возможных объяснений.
1. Способность человека производить качественные разграничения хорошо представлена пятью определениями: слабый, равный, сильный, очень сильный, абсолютный. Для большей точности можно пользоваться промежуточными определениями.
2. Классификация по трем основным зонам – неприятие, безразличие, приятие, каждая из которых делится на низкую, умеренную и высокую степени.
3. Психологический предел 7 ± 2 предметов при одновременном сравнении подтверждает, что если взять7 ± 2 отдельных предметов, близких относительно свойства, используемого для сравнения, то требуется 9 точек, чтобы их различить.
Замечание. Здесь уместно упомянуть и о принятой в отечественном образовании системе оценок 3, 4 и 5 с ее градациями 3 ±, 4 ±, 5 ±.
Опишем один из способов того, как практически придать количественное наполнение сравнению объектов, действий или обстоятельств и построить соответствующую таблицу сравнений.
Пусть даны элементы А, В, С, D и т. д.
Таблица сравнений, имеющая вид
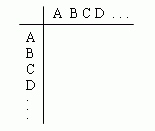
строится по следующим правилам:
если А и В одинаково важны, заносим в позицию (А,В) таблицы сравнений число 1,
если А незначительно важнее В – число 3,
если А значительно важнее В – число 5,
если А явно важнее В – число 7,
если А по своей значимости абсолютно превосходит В – число 9.
Числа 2, 4, 6 и 8 используются для облегчения компромиссов между оценками, слегка отличающимися от основных чисел.
Рациональные дроби используются в случае, когда желательно увеличить согласованность всей матрицы при малом числе суждений.
Пример. Предположим, что сравнивая объекты А, В, С и D, мы получили таблицу сравнений

которая приводит к обратно-симметричной матрице, рассмотренной выше.
Опишем несколько способов приближенного вычисления собственного столбца.
1-й способ:
1) суммируем элементы каждой строки и записываем полученные результаты в столбец,
2) складываем все элементы найденного столбца,
3) делим каждый из элементов этого столбца на полученную сумму.
2-й способ:
1) суммируем элементы каждого столбца и записываем полученные результаты в столбец,
2) заменяем каждый элемент построенного столбца на обратный ему,
3) складываем элементы столбца из обратных величин,
4) делим каждый из этих элементов на полученную сумму.
3-й способ:
1) суммируем элементы каждого столбца,
2) делим элементы каждого столбца на их сумму,
3) складываем элементы каждой строки полученной матрицы,
4) записываем результаты в столбец,
5) делим каждый из элементов последнего столбца на порядок исходной матрицы п.
4-й способ:
1) перемножаем элементы каждой строки и записываем полученные результаты в столбец,
2) извлекаем корень n-й степени из каждого элемента найденного столбца,
3) складываем элементы этого столбца,
4) делим каждый из этих элементов на полученную сумму.
Каждый из этих четырех способов, будучи примененным к идеальной матрице, приводит к одному и тому же точному результату.
Пользуясь одним из способов приближенного вычисления собственных элементов этой матрицы (для определенности вторым), мы нашли и собственный столбец и собственное значение, и ИС:
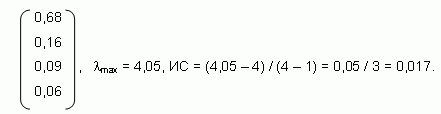
Сумма всех элементов полученного собственного столбца (его называют столбцом приоритетов) равна 1. Он позволяет подвести итог проведенному анализу таблицы сравнений:
среди сравниваемых элементов А, В, С и D наивысший приоритет имеет А (68%), затем идут В (16%), С (9%) и D (6%) соответственно.
Иерархии
Очень часто при анализе интересующей нас структуры число элементов и их взаимосвязей настолько велико, что превышает способность исследователя воспринимать информацию в полном объеме. В таких случаях система делится на подсистемы. Одним из таких делений является иерархическое.
Первым требованием при анализе функционирования системы является построение иерархии, воспроизводящие функциональные отношения. Для этого сначала перечисляются все элементы, относящиеся к иерархии. Затем они распределяются по группам в соответствии с влиянием между группами. Так возникают уровни иерархии. Определяются цели, ради которых изучается задача, и строится иерархия.
После того, как уровни иерархии заданы, составляются матрицы попарных сравнений между этими элементами относительного каждого элемента следующие, более высокого уровня, который служит критерием при сравнении. Приведем пример типичной иерархии (рис. 1.1). Первый уровень иерархии имеет одну цель: общее благосостояние страны. Второй уровень иерархии имеет три цели: сильную экономику, здравоохранение, национальную оборону. Приоритеты этих целей получаются в матрице попарных сравнений относительно цели первого уровня. Целями третьего уровня являются отрасли промышленности.
Задача заключается в определении влияния отраслей промышленности на общее благосостояние страны через промежуточный второй уровень. Поэтому приоритеты отраслей промышленности относительно каждой цели второго уровня получаются из матриц попарных сравнений относительно этих целей, а полученные столбцы приоритетов взвешиваются затем при помощи столбца приоритетов второго уровня, что позволяет получить в итоге искомый составной столбец приоритетов отраслей промышленности.

рис. 1.1. рис. 1.2.
Пример (распределение энергии). Предположим, что нам необходимо разрешить проблему распределения энергии в некоторой развитой стране между тремя ее крупнейшими пользователями: бытовым потреблением (БП), транспортом (ТР) и промышленностью (ПР). Они составляют третий, или низший уровень иерархии. Целями, по отношению к которым оцениваются эти потребители, являются вклад в развитие экономики (Э), вклад в качество окружающей среды (С) и вклад в национальную безопасность (Б). Цели составляют второй уровень иерархии. Общая цель – благоприятное социальное и политическое положение (Бл) – первый уровень иерархии (рис. 1.2).
Построим матрицу попарных сравнений 3-х целей: Э, С и Б в соответствии с их воздействием на общую цель – Бл. Умышленно навязывая согласованность создаваемой матрице, мы по первой строке находим все остальные ее элементы. Имеем:
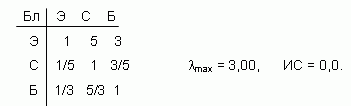
Необходимые пояснения к таблице. Экономика имеет сильное превосходство перед окружающей средой (5) и слабое перед национальной безопасностью (3). Числа во 2-й и 3-й строках выбраны так, чтобы полученная матрица сравнений была обратно-симметричной и согласованной.
С
 толбец приоритетов, вычисленный любым из описанных выше способов, имеет вид
толбец приоритетов, вычисленный любым из описанных выше способов, имеет вид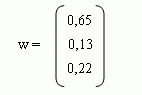
Следовательно, в соответствии со сравнением по социально-политическому влиянию экономика получает приоритет 0,65, окружающая среда – 0,13 и национальная безопасность – 0,22 (рис. 2.3).
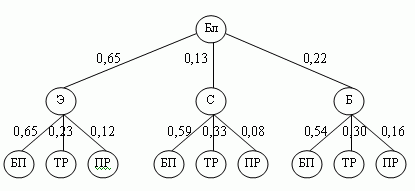
рис. 1.3.
Приведем теперь оценку относительной важности каждого потребителя с точки зрения экономики, окружающей среды и национальной безопасности (составляющих второй уровень иерархии).
Соответствующие матрицы попарных сравнений, индексы согласованности и столбцы приоритетов имеют следующий вид:
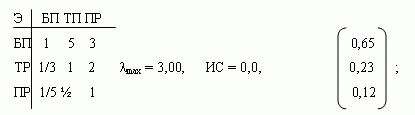
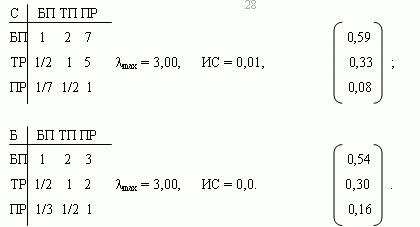
Запишем полученные столбцы в виде матрицы. Имеем
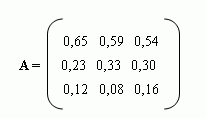
Умножая эту матрицу на столбец w, находим искомый столбец приоритетов третьего уровня иерархии, представляющего потребителей энергии БП, ТР и ПР (взвешенный согласно их общему влиянию):

0,62
Р = 0,26
0,12
Итак, в соответствии с нашими вычислениями на бытовое потребление следует выделить 62% энергии, на транспорт – 26% и на промышленность – 12%.
Особенно тщательно должны устанавливаться приоритеты высших уровней иерархии, так как для них наиболее необходим консенсус, ввиду того, что эти приоритеты – ведущие в иерархии. На каждом уровне должна быть обеспечена независимость представляемых критериев, или, по крайней мере, критерии должны достаточно различаться, и эти различия могут быть зафиксированы как независимые характеристики на уровне. Для успешного фиксирования независимости может оказаться необходимым пересмотр элементов. Этот подход можно распространить и на взаимосвязь критериев, когда зависимость является внутренним свойством и ею нельзя пренебречь. При движении вниз по иерархии ожидается большее непостоянство во мнениях между, в общем-то, совместимыми людьми при достижении операционного уровня. В области, где люди сходятся во взглядах как на смысл, так и на важность элементов следует размещать больше ресурсов; в той же области, в которой люди расходятся во взглядах на смысл или важность, их суждения имеют тенденция сводить на нет мнения друг друга, и данная область получит меньшую долю действия до тех пор, пока не будет оказана сильная поддержка. Если область важна, но в ней имеется расхождение во мнениях, то следует воздержаться от действий до тех пор, пока люди лучше не разберутся во взглядах и не придут к согласованному действию. Это является логическим исходом иерархического подхода. Там, где есть расхождение, люди будут неудовлетворенными, так как они не встречают понимания своих суждений. С другой стороны, если взгляды сходятся, то люди испытывают удовлетворение.
