«Реализация метода оптимизация функции нескольких переменных (метод покоординатного спуска) в Excel»
| Вид материала | Лабораторная работа |
СодержаниеМетод покоординатного спуска. Реализация метода покоординатного спуска в Excel. |
- Пояснительная записка к курсовому проекту на тему «Оптимизация функции двух переменных, 137.41kb.
- Отчет по дисциплине «методы оптимизации и принятия решения» на тему «лабораторная работа, 23.84kb.
- Задачи оптимизации с ограничениями в виде неравенств. Постановка задачи. Геометрические, 42.48kb.
- Примерная программа государственного экзамена по направлению подготовки дипломированных, 196.44kb.
- Лекция 19. Предел и непрерывность функции нескольких переменных, 34.61kb.
- Курсовая работа по численным методам «Минимизация функций нескольких переменных. Метод, 273.76kb.
- Программа дисциплины «математический анализ», 432.47kb.
- Программа дисциплины «Математический анализ», 500.52kb.
- Факультет: авт группа: ас-513, 488.24kb.
- Календарно-тематический план учебная дисциплина: «Математика», 35.73kb.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОУВПО «Самарский государственный архитектурно-строительный университет»
Факультет информационных систем и технологий
Кафедра прикладной математики и вычислительной техники
Лабораторная работа №3
по дисциплине
МЕТОДЫ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ
На тему
«Реализация метода оптимизация функции нескольких переменных (метод покоординатного спуска) в Excel»
6 СЕМЕСТР 3 КУРС
Руководитель: Пиявский С.А.
| Проверил: | Выполнил студент ГИП-105 Косов Д.С. |
| Пиявский С.А. __________________ | _______________________ |
Общая оценка __________
Методический руководитель _______________________
Цель: Найти относительный минимум функции, используя метод покоординатного спуска.
Функция имеет вид:
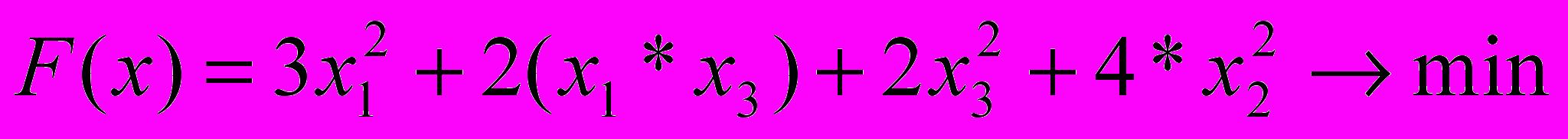
Метод покоординатного спуска.
Пусть нужно найти наименьшее значение целевой функции u=f(M)=f(x, x, . . . ,xn). Здесь через М обозначена точка n-мерного пространства с координатами x, x, . . . ,xn: M=(x, x, . . . ,xn). Выберем какую-нибудь начальную точку М=(x, x, . . . ,xn0) и рассмотрим функцию f при фиксированных значениях всех переменных, кроме первой: f(x, x,x, . . . ,xn0 ). Тогда она превратится в функцию одной переменной x . Изменяя эту переменную, будем двигаться от начальной точки x=x в сторону убывания функции, пока не дойдем до ее минимума при x=x, после которого она начинает возрастать. Точку с координатами ( x, x,x, . . . ,xn0) обозначим через М, при этом f(M0) f(M).
Фиксируем теперь переменные: x=x, x= x, . . . ,xn=xn0 и рассмотрим функцию f как функцию одной переменной x. Изменяя x , будем опять двигаться от начального значения x2=x20 в сторону убывания функции, пока не дойдем до минимума при x2=x21 .Точку с координатами {x, x, x . . . xn0} обозначим через М, при этом f(M1) f(M).Проведем такую же минимизацию целевой функции по переменным x1, x2, . . . ,xn. Дойдя до переменной xn, снова вернемся к x и продолжим процесс. Эти действия следует повторять до тех пор, пока уменьшение функции не станет меньше или равно заданной нами точности е.
Реализация метода покоординатного спуска в Excel.
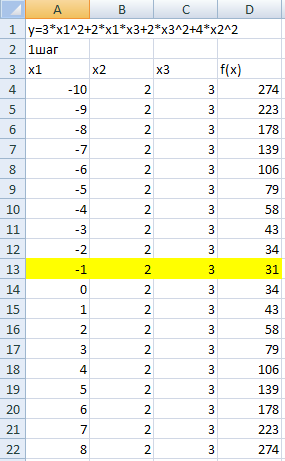
Рисунок 1 – Изменяем переменную x1 в промежутке от -10 до 10 с шагом 1. На первом шаге минимум функции f(x)=31 и достигнут при значениях переменных x1=-1, x2=2 и x3=3.
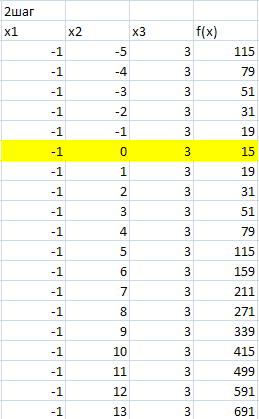
Рисунок 2 – Изменяем переменную x2 в промежутке от -5 до 13 с шагом 1. На втором шаге минимум функции f(x)=15 и достигнут при значениях переменных x1=-1, x2=0 и x3=3.
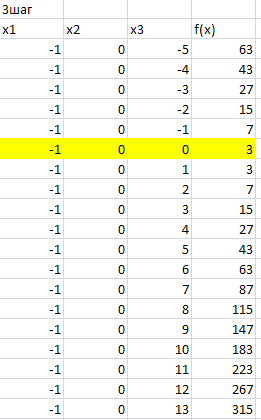
Рисунок 3 – Изменяем переменную x3 в промежутке от -5 до 13 с шагом 1. На третьем шаге минимум функции f(x)=3 и достигнут при значениях переменных x1=-1, x2=0 и x3=0.
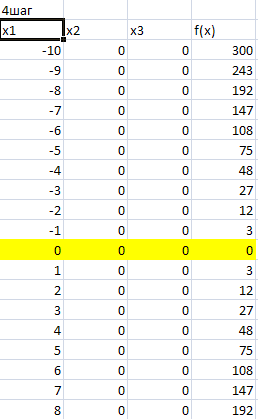
Рисунок 4 – Изменяем переменную x1 в промежутке от -10 до 8 с шагом 1. На четвертом шаге минимум функции f(x)=0 и достигнут при значениях переменных x1=0, x2=0 и x3=0.
Продолжаем изменения, до того момента, пока не будет достигнута заданная точность.
Вывод: Изучил покоординатный метод поиска минимума, реализовав его в Excell.
Литература
1. Методы оптимизации и принятия решений: методические указания к выполнению лабораторных работ / сост. С.А.Пиявский; Самарск. гос. арх.-строит. ун-т./ - Самара, 2007. 59 с.
