Отчет по дисциплине «методы оптимизации и принятия решения» на тему «лабораторная работа №5. Программная реализация методов оптимизации функции нескольких переменных (метод ньютона)»
| Вид материала | Отчет |
СодержаниеОписательная часть. Реализационная часть. |
- Отчет по дисциплине «методы оптимизации и принятия решения» на тему «лабараторная работа, 20.92kb.
- Отчет по дисциплине «методы оптимизации и принятия решения» на тему «лабараторная работа, 20.52kb.
- Программа дисциплины «математический анализ», 432.47kb.
- Программа дисциплины «Математический анализ», 500.52kb.
- Рабочая учебная программа по дисциплине «Методы оптимизации» Направление №230100 «Информатика, 129.28kb.
- Программа дисциплины " методы оптимизации " Направление, 59.57kb.
- Задачи оптимизации с ограничениями в виде неравенств. Постановка задачи. Геометрические, 42.48kb.
- Повторение. Аналитические методы оптимизации функций одной и нескольких переменных, 250.23kb.
- Ния методики интерактивного поиска минимума функции многих переменных к задаче оптимизации, 35.39kb.
- Календарно-тематический план учебная дисциплина: «Математика», 35.73kb.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
“САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕСИТЕТ”
ФАКУЛЬТЕТ ИНФОРМАЦИОННЫХ СИСТЕМ И ТЕХНОЛОГИЙ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
ОТЧЕТ ПО ДИСЦИПЛИНЕ
«МЕТОДЫ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЯ»
НА ТЕМУ
«ЛАБОРАТОРНАЯ РАБОТА №5. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ МЕТОДОВ ОПТИМИЗАЦИИ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ (МЕТОД НЬЮТОНА)»
ВЫПОЛНИЛ СТУДЕНТ ГИП-105:
ГОРЯЧЕВ А.А.
( )
ПРЕПОДАВАТЕЛЬ:
ПИЯВСКИЙ С.А.
( )
ОЦЕНКА:
САМАРА
2008
Задание.
Реализовать программу для оптимизации функции нескольких переменных методом Ньютона.
Описательная часть.
В качестве среды реализации данного метода я выбрал Microsoft Visual Studio 2005, в качестве языка VB.NET.
При написании алгоритма использовалась методика процедурного программирования.
На данный момент программа реализована только для функций с тремя переменными. Но ее легко перенастроить и на работу с n переменными, т.к. она работает на динамических массивах.
Метод Ньютона – наиболее распространенный метод для решения систем нелинейных уравнений. Он обеспечивает более быструю сходимость, чем другие методы. Т.к. использует вторые производные. В основе метода Ньютона лежит представление всех n уравнений исходной системы в виде рядов Тейлора.
Если бы использованное аналитическое выражение было точным представлением оптимизируемой функции, полученное соотношение сразу дало бы точку оптимума. Поскольку же это не так, оно дает лишь k + 1 –е приближение
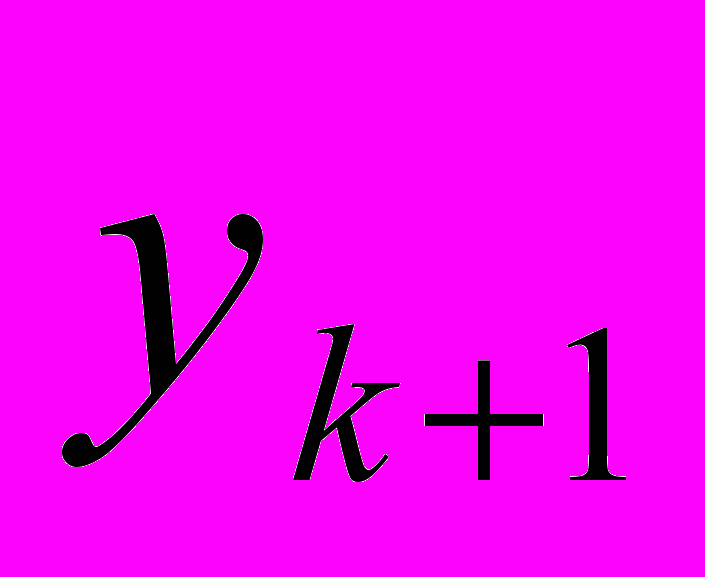. Поэтому ведем расчет пока не достигнем заданной точности.Дважды дифференцируемую выпуклую функцию в окрестности точки оптимума можно приближенно представить в виде
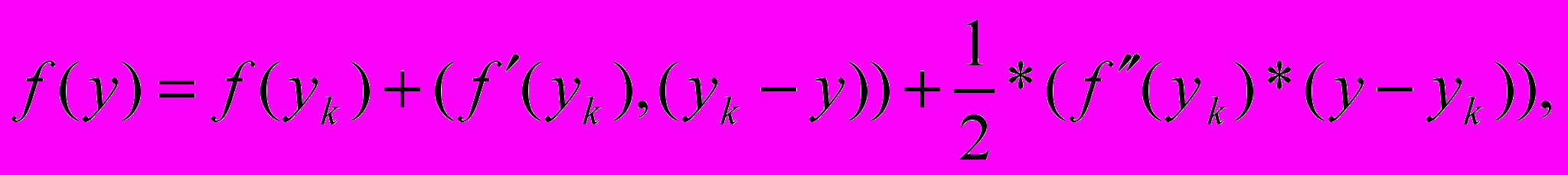
где
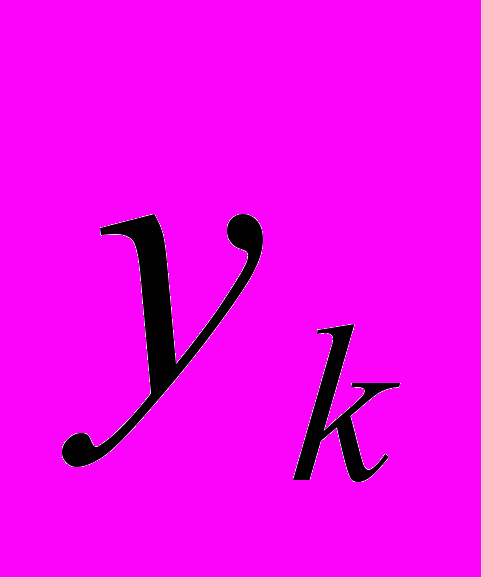- k - е приближение, 
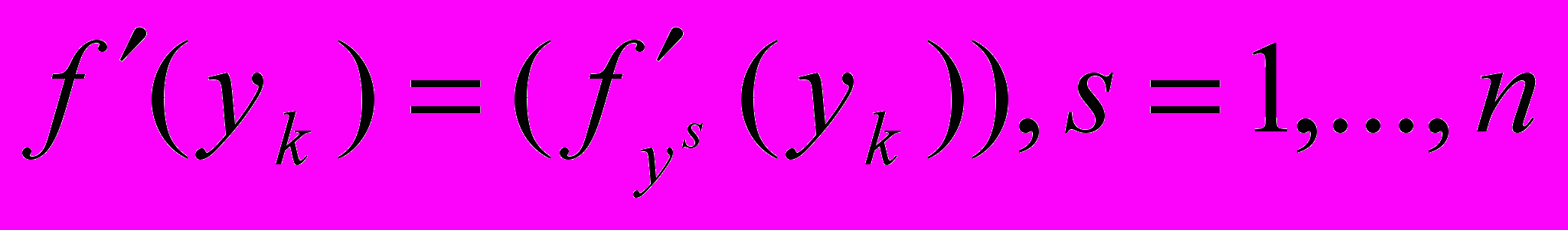- градиент функции в точке , 
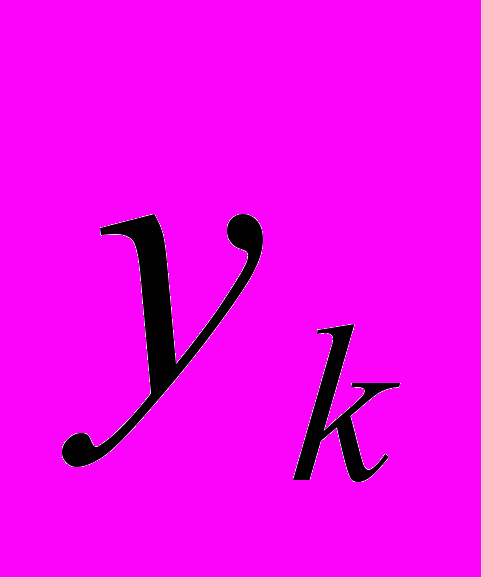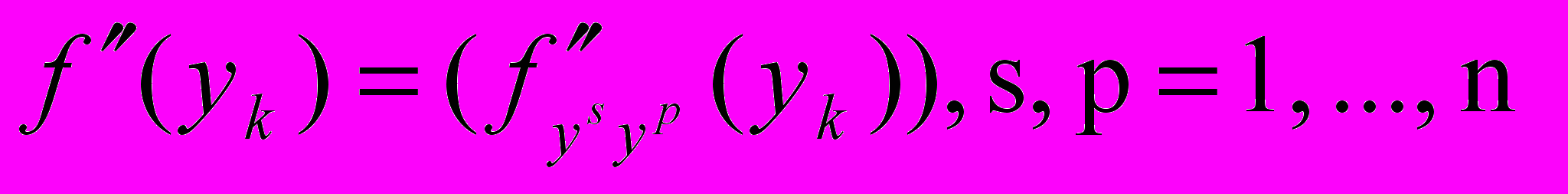- матрица вторых производных функции в точке 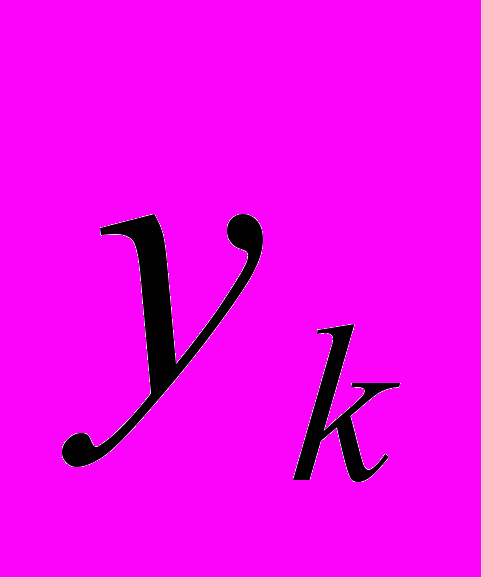.Для этой аналитически заданной функции можно найти точку минимума, используя необходимые условия оптимальности:
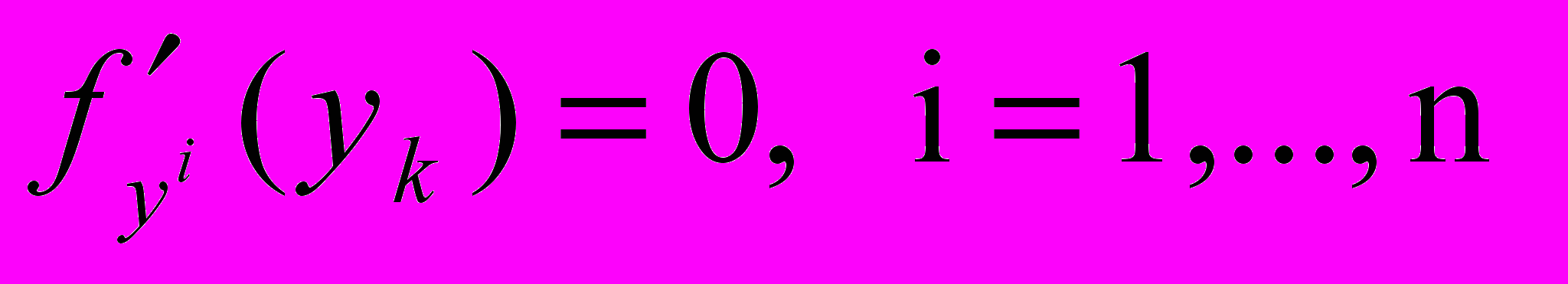.Они приведут к уравнению (векторному)
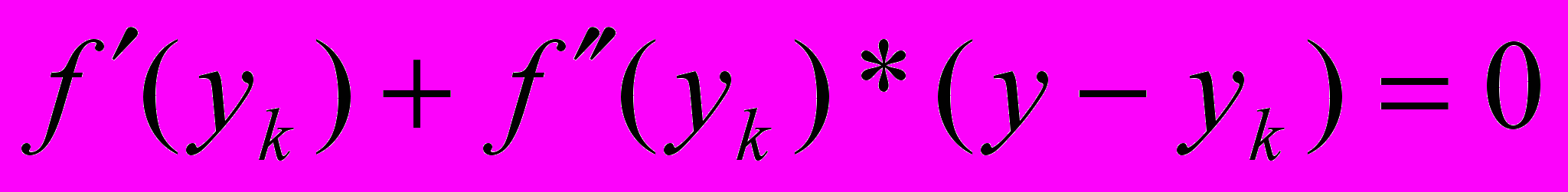,откуда
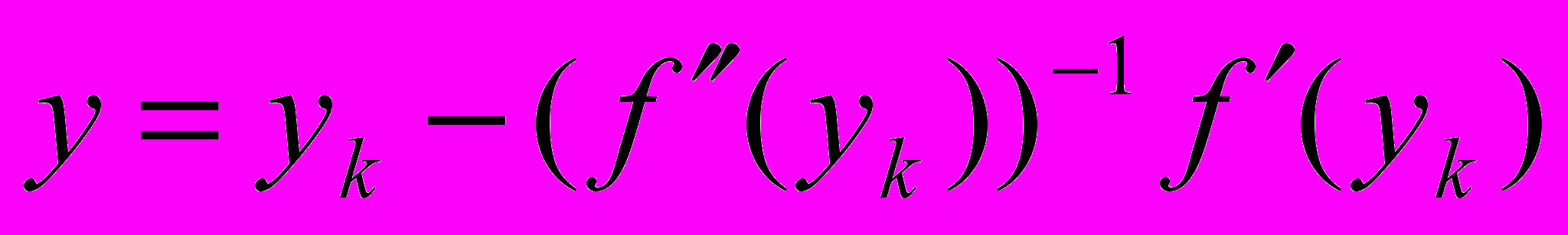,где
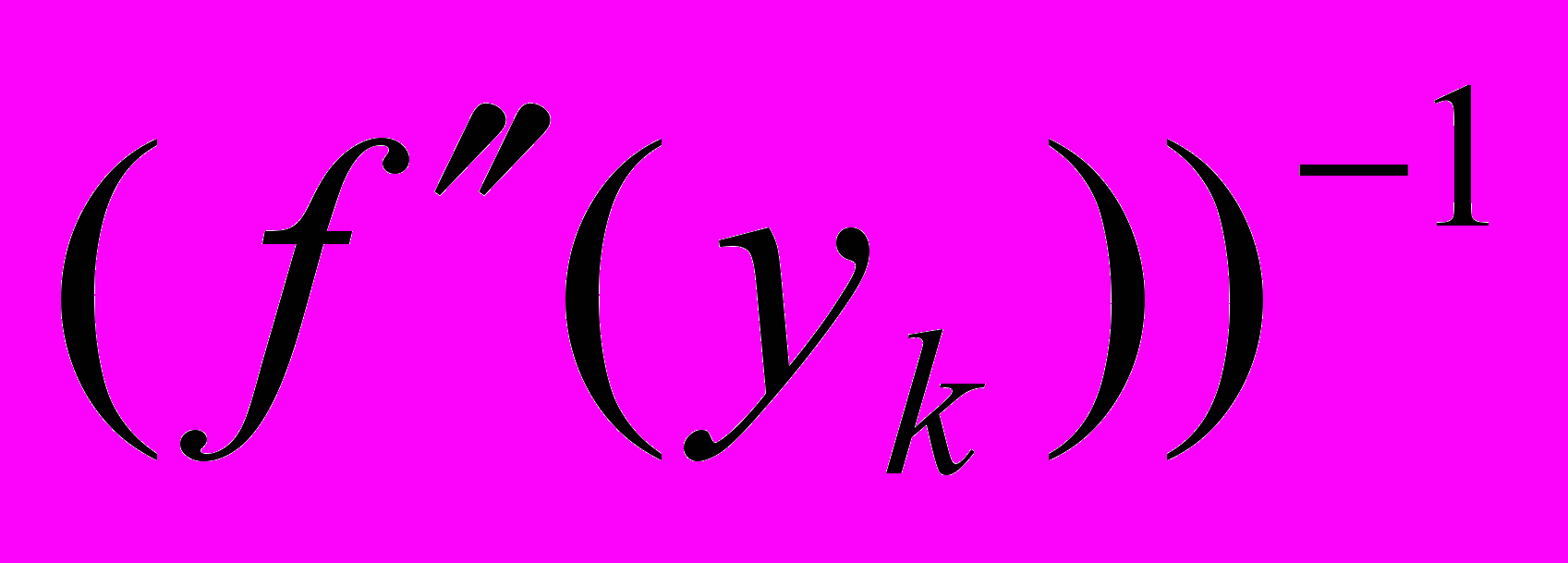- обратная матрица вторых производных. На каком-то определенном шаге вычисления достигнут заданной точности и вектор у будет считаться минимумом функции.
Реализационная часть.
Воспользуемся приложением Mathcad для проверки метода.
Пример.
Результат посчитанный созданной программой.
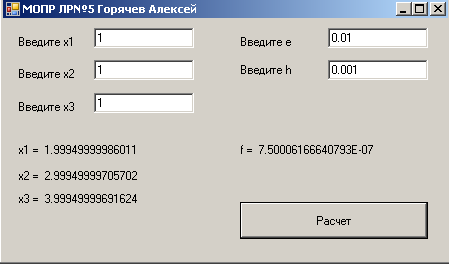
Как видно из представленных вычислений метод реализован корректно.
Открыть модель
Литература
1. Методы оптимизации и принятия решений: методические указания к выполнению лабораторных работ / сост. С.А.Пиявский; Самарск. гос. арх.-строит. ун-т./ - Самара, 2007. 59 с.