Отчет по дисциплине «методы оптимизации и принятия решения» на тему «лабараторная работа №3. Программная реализация методов оптимизации функции одной переменной (метод золотого сечения)»
| Вид материала | Отчет |
СодержаниеМатематическая модель. |
- Отчет по дисциплине «методы оптимизации и принятия решения» на тему «лабараторная работа, 20.92kb.
- Отчет по дисциплине «методы оптимизации и принятия решения» на тему «лабораторная работа, 23.84kb.
- Рабочая учебная программа по дисциплине «Методы оптимизации» Направление №230100 «Информатика, 129.28kb.
- Программа дисциплины " методы оптимизации " Направление, 59.57kb.
- Оптимизация технологических процессов методические указания и задания к контрольным, 349.61kb.
- Конспект лекций по Методам оптимизации для студентов, обучающихся по специальности, 41.05kb.
- Методы оптимизации. Вопросы к экзамену, 26.98kb.
- Календарный план учебных занятий по дисциплине Компьютерный дизайн оптических наноструктур,, 39.38kb.
- Алтайский Государственный Технический Университет им. И. И. Ползунова памятка, 129.3kb.
- Концепция системного подхода при проектировании сапр. Последовательный метод компоновки, 29.25kb.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
“САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕСИТЕТ”
ФАКУЛЬТЕТ ИНФОРМАЦИОННЫХ СИСТЕМ И ТЕХНОЛОГИЙ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
ОТЧЕТ ПО ДИСЦИПЛИНЕ
«МЕТОДЫ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЯ»
НА ТЕМУ
«ЛАБАРАТОРНАЯ РАБОТА №3
.ПРОГРАММНАЯ РЕАЛИЗАЦИЯ МЕТОДОВ ОПТИМИЗАЦИИ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ (МЕТОД ЗОЛОТОГО СЕЧЕНИЯ)»
ВЫПОЛНИЛ СТУДЕНТ ГИП-105:
СИМОНОВ Н.А.
( )
ПРЕПОДАВАТЕЛЬ:
ПИЯВСКИЙ С.А.
( )
ОЦЕНКА:
САМАРА
2007
Задание.
Найти минимум функции
методом золотого сечения на отрезке [a,b]. Составить программу для реализации данного задания, где a и b задаются пользователем.Математическая модель.
Метод золотого сечения применяется для поиска минимума функции одного переменного на отрезке. Метод использует следующее свойство непрерывных функций: если точки g и h (g < h) расположены на (a, b) и f(g) ≤ f(h), то на отрезке [a, h] есть хотя бы один минимум функции. Аналогично, если f(g) ≥ f(h), то на отрезке [g, b] есть хотя бы один минимум.
Метод золотого сечения выбирает на отрезке две симметричные точки:
и 
. Применяется указанная выше процедура, приводящая к отрезку [A, h] или [g, B] (для определенности рассмотрим первый вариант). Если повторить указанную процедуру, то можно опять уменьшить отрезок. Важным свойством алгоритма является то, что на каждом шаге можно использовать одно значение функции из предыдущего шага, т.к. при новом разбиении отрезка [A, h] точками h' и g', мы увидим, что h' = g. Т.е. на каждом шаге вычисляется только одно значение функции (и ещё два в самом начале работы). Метод обладает стабильной линейной скоростью сходимости, не зависящей от рельефа функции.
Воспользуемся приложением Mathcad для построения графика функции и нахождения промежутка унимодальности.
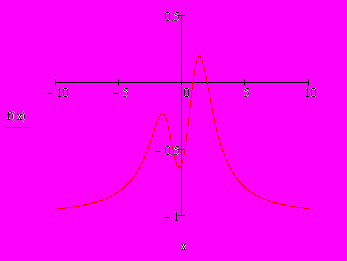
Проверим результаты в Excel.
Графики одинаковы и из низ становится понятно, что функции имеет один действительный минимум. Участком унимодальности будем считать [-1;1].
Пример.
Результат посчитанный созданной программой.
Результат посчитанный в Excel.
Литература
1. Методы оптимизации и принятия решений: методические указания к выполнению лабораторных работ / сост. С.А.Пиявский; Самарск. гос. арх.-строит. ун-т./ - Самара, 2007. 59 с.