Алтайский Государственный Технический Университет им. И. И. Ползунова памятка
| Вид материала | Памятка |
- Метод расчета и проектирования солнечной теплицы для региона сибири, 330.99kb.
- Оценка полученных знаний, навыков, способностей и их важность для профессиональной, 323.76kb.
- Врамках работы секции планируется обсудить следующие вопросы: Оборудование, процессы, 39.67kb.
- О проведении открытого аукциона в электронной форме, 866.61kb.
- Печатная реклама в01 – социальная реклама, 1030.65kb.
- Уважаемые выпускники 2011 года, 182.29kb.
- Научное обоснование и практическая реализация комплексного применения биологически, 740.94kb.
- Параметры программы Характеристика 1 Название образовательного учреждения гоу впо «Алтайский, 25.22kb.
- Учебное пособие Министерство общего и профессионального образования Российской Федерации, 936.13kb.
- И. И. Ползунова Стуров Д. С., Белоусова Н. Н., Авдеев Е. Н. Определение загрязненности, 481.1kb.
Алтайский Государственный Технический Университет
им. И.И. Ползунова
Памятка для студентов групп ПОВТ по изучению дисциплины
«Методы оптимизации».
(4 семестр)
Составила Бразовская Н.В.. Утверждаю
Зав. Кафедрой__________
1 02 2006 года
1. Содержание дисциплины.
В 4-ем семестре будут рассмотрены темы.
Модуль 1. Математическое программирование
Тема 1.. Понятие о математическом программировании: постановка задачи оптимизации, критерий оптимальности, область допустимых решений, классификация задач и методов оптимизации, методы одномерной оптимизации.
Литература [1,2,4,5,7,9]
^ Модуль 2. линейное программирование
Тема 2. Общая задача линейного программирования: постановка задачи линейного программирования, различные эквивалентные формы задач линейного программирования, геометрическая интерпретация задачи линейного программирования.
Литература [1,3,4,7,9]
^ Тема 3. Элементы теории выпуклых множеств и выпуклых функций: выпуклая комбинация, выпуклое множество, граничные точки, крайние точки, выпуклый многогранник, конус, симплекс, выпуклая функция, теоремы выпуклости о допустимой области решения задачи линейного программирования.
Литература [1,4,5,7,9]
^ Тема 4. Свойства решений задачи линейного программирования: определение опорного плана, оптимального плана, теоремы о крайних точках, построение опорных планов.
Литература [1,4,5,7,9]
^ Тема 5. Симплекс метод: теоремы о признаке оптимальности, алгоритм симплекс-метода, симплекс таблицы, метод искусственного базиса, геометрическая интерпретация симплекс метода.
Литература [1,4,5,6,9]
Тема 6. Двойственность в линейном программировании: несимметричные и симметричные двойственные задачи, интерпретация двойственных оценок, теоремы двойственности.
Литература [1,4,5,6,9]
Модуль 3. Специальные задачи и методы линейного программирования
Тема 7. Транспортные задачи и методы их решения: постановка задачи транспортного типа, основные теоремы, метод северо-западного угла, метод потенциалов.
Литература [1,4,5,6,7]
Тема 8. Дискретное программирование (задача о назначениях): постановка задачи о назначениях, венгерский метод.
Литература [1,10]
^ Тема 9. Задачи целочисленного программирования: постановка задачи целочисленного программирования, методы решения задачи целочисленного программирования метод отсечения Гомори.
Литература [1,4,7,8]
Модуль 4. динамическое программирование:
Тема 10. Задачи динамического программирования: постановка задачи динамического программирования, принцип Беллмана, локальный и глобальный экстремум, методы решения задач динамического программирования с учетом предыстории процесса, с мультипликативным критерием,
Литература [1,4,5,7,8,10]
^ Модуль 5. Нелинейное программирование:
Тема 11. Задачи нелинейного программирования: основные понятия нелинейного программирования, методы решения задач нелинейного программирования без ограничений (градиентные, овражные), теорема Куна Таккера, методы решения задач нелинейного программирования с ограничениями (множителей Лагранжа, штрафных функций возможных направлений).
Литература [2,3,4,7]
^ 2. Литература и учебно-методические материалы.
Основная литература:
1 Бразовская Н.В., Бразовская О.В. Методы оптимизации: Учебное пособие / Алт. Госуд. Технич. Унт им. И.И.Ползунова.Барнаул. изд. АлтГТУ, 2006. 127 с.(300 экз.)
2 Васильев Ф.П. Численные методы решения экстремальных задач: Учеб. пособие для вузов. М.: Наука, 1988. 552 с.(30 экз)
.3 Черноруцкий Н.Г. Методы оптимизации и принятие решений: Учебное пособие. - , СПб.: Издательство "Лань", 2002. - 384 с.(10 экз)
.4 Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование. Минск: Вышейшая школа, 1994. 286 с.(20 экз)
Дополнительная литература
5 Ашманов С.А., Тимохов А.В. Теория оптимизации в задачах и упражнениях. М.: Наука, 1991. 446 с.
6.Математическое программирование / Под ред. Н.Ш. Кремера. М.: Финстатинформ, 1995.
7 Мину М. Математическое программирование: Теория и алгоритмы./ пер. с фр. И.Штерна. М.: Наука, 1990. 485 с.
.8.Акулич И.Л. Математическое программирование в примерах и задачах. М.: Высшая школа, 1993..
9.Гасс С. Линейное программирование. М.: Физико-математическая литература 1961. 300 с.
10 Зайченко Ю.П. Исследование операций: Учебное пособие. Киев: Вища школа, 1991. 191 с.
| ^ Виды индивидуальной деятельности при изучения курса «Методы оптимизации» | Число баллов (максимум) |
| 1) посещение лекций и лабораторных занятий в течение семестра; 2) сдача лабораторных работ в установленный срок; 3) выполнение контрольной работы №1 4) выполнение контрольной работы №2 5) выполнение и защита расчетного задания по дисциплине; 5) выполнение теста по теории 6) зачет Итого | 5 (0,05) 30 (0,3) 10(0,1) 10 (0,1) 10 (0,1) 10 (0,1) 25(0,25) 100(1) |
^ 3.Контрольные точки
| Номер недели | Модуль | Номер темы | Лекции | Лабораторные | Форма контроля | Вес в итоговом рейтинге | |
| Номер | Наименование | ||||||
| 1 | 1 | 1 | 1 | 1 | Одномерная оптимизация | Лаб. раб. Защита | 0,05 |
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | 2 | 2 | 2 | 2 | Графическое решение ЗЛП” | Лаб. раб. Защита | 0.02 |
| 6 | |||||||
| 3 | 2 | 3 | Построение опорных планов | Лаб. раб Защита | 0,02 | ||
| 7 | |||||||
| 8 | |||||||
| 4 | 3 | 4 | Смплекс - метод | Лаб. раб. Защита Ат.1 | 0.02 | ||
| 9 | |||||||
| 5 | 3 | 5 | Метод искусственного базиса | Лаб. раб. Защита | 0.02 | ||
| КР 1. | 0,1 | ||||||
| 6 | 4 | 6 | Двойственные ЗЛП | Лаб. раб. Защита | 0.02 | ||
| 10 | 3 | 7 | 5 | 7 | Транспортные задачи | Лаб раб. Защита | 0.02 |
| 11 | |||||||
| 8 | 6 | 8 | Задачи о назначениях | Лаб. раб. Защита | 0,02 | ||
| 12 | |||||||
| 9 | 6 | 9 | Целочисленные ЗЛП | Лаб. раб. Защита | 0.02 | ||
| КР 2 | 0,1 | ||||||
| 13 | 4 | 10 | 7 | 10 | Задачи динамического программирования | Лаб раб Защита Ат.2 | 0.03 |
| 14 | |||||||
| 15 | 5 | 11 | 8 | 11 | Методы безусловной оптимизации | Лаб. раб Защита | 0,03 |
| 16 | 12 | ||||||
| Защита РЗ | 0,1 | ||||||
| 17 | |||||||
| 12 | 8 | 12 | Методы условной оптимизации | Лаб. раб Защита | 0,03 | ||
| Тест | 0,1 | ||||||
| Зачетная неделя | Зачет | 0,25 | |||||
Примечание.
- При защите лабораторных работ и расчетного задания, написании контрольных работ и теста по теории ответ оценивается из 100 бальной шкалы оценок:
- 0 - 24 неуд
- 25 - 49 удовлетворительно
- 50 – 74 хорошо
- 75 и выше отлично
- К первой аттестации должны быть защищены 1-4 работы, ко второй – 5-9, остальные к дате проведения Зачета.
- Защита лабораторной после установленного срока, оценивается на 10% ниже.
- Оценка защиты 80 и выше баллов ставится при выполнении задания несколькими вариантами и обстоятельном объяснении своих действий.
- На зачет «автомат» имеют право студенты, у которых защищены все лабораторные работы, написаны контрольные работы на положительные оценки, защищено расчетное задание и семестровый рейтинг Rсем>= 75
- Порядок вычисления рейтинга:.
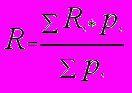 , где
, гдеRi –оценка за i-ю контрольную точку,
pi – вес этой контрольной точки,
i – номер контрольной точки.
Суммирование проводится по всем контрольным точкам с начала семестра до момента вычисления рейтинга.
Замечание: Успеваемость студента во время аттестации оценивается с помощью текущего рейтинга по этой же формуле.
Пример определения рейтинга студента Сидорова в течение семестра.
| № лаб | Вес в итог. Рейтинге | Срок защиты | Факт защита | Оценка защиты | Нарушение | Отклонен в % | Итоговая оценка |
| 1 | 0,05 | 4 нед. | 2 нед | 42 | | | 42 |
| 2 | 0,02 | 5 нед. | 6 нед | 51 | Не в срок | -10% | 46 |
| 3 | 0,02 | 6 нед | 5 нед | 51 | | | 51 |
| 4 | 0,02 | 7 нед. | 6 нед | 54 | | | 54 |
| 5 | 0,02 | 8 нед. | 10 нед | 59 | Не в срок | -10% | 53 |
| 6 | 0,02 | 9 нед. | 9 нед | 53 | | | 53 |
| 7 | 0,02 | 10 нед. | 10 нед | 50 | | | 50 |
| 8 | 0,02 | 11 нед | 11 нед | 57 | | | 57 |
| 9 | 0,02 | 12 нед | 12 нед | 56 | | | 56 |
| 10 | 0,03 | 14 нед | 14 нед | 60 | | | 60 |
| 11 | 0,03 | 16 нед. | 16 нед | 70 | | | 70 |
| 12 | 0,03 | 17 нед. | 17 нед | 63 | | | 63 |
| КР 1 | 0,1 | 8 нед. | 8 нед. | 67 | | | 67 |
| КР 2 | 0,1 | 12 нед. | 14 нед. | 55 | Не в срок | -10% | 50 |
| РЗ | 0,1 | 16 нед. | 17 нед | 65 | Не в срок | -10% | 58 |
| Тест | 0,1 | 17 нед | 17 нед | 70 | | | 70 |
| Зачет | 0,25 | | | 65 | | | 65 |
На 1-й аттестации(7 неделя).
Rат1 = (42*0,05 +46*0,02+51*0,02+54*0,02)/ (0,05+0,02+0,02+0,02) = 47
На 2-й аттестации(13 неделя.).
Rат2 = (42*0,05+46*0,02+51*0,02+54*0,02+53*0,02+53*0,02+50*0,02+57*0,02+56*0,02+67*0,1+50*0,1)/ (0,05+0,02+0,02+0,02+0,02+0,02+0,02+0,02+0,02+0,1+0,1) = 53
Перед началом сессии вычисляется семестровый рейтинг.
Rсем=(42*0,05+46*0,02+51*0,02+54*0,02+53*0,02+53*0,02+50*0,02+57*0,02+56*0,02+67*0,1+50*0,1+60*0,03+70*0,03+63*0,03+58*0,1+70*0,1) / (0,05+0,02+0,02+0,02+0,02+0,02+0,02+0,02+0,02+0,1+0,1+0,03+0,03+0,03+0,1+0,1) = 59
Таким образом, семестровый рейтинг студента равен 59 баллов.
Итоговый рейтинг, учитывающий зачет,
Rитог=59*0,7+65*0.25+d.
Добавка d = 5, если посещены все лекции и выполнены в срок все лабораторные работы, в противном случае d =0.
Студент Сидоров не все работы выполнял в срок, потому не получает дополнительных 5 баллов. И его итоговый рейтинг равен 59 баллов.
Примечание: студент, имеющий высокий рейтинг, может его повысить свой, выполнив расчетное задание в виде исследовательской работы.
