Geum.ru

Календарный план учебных занятий по дисциплине Компьютерный дизайн оптических наноструктур, нп-5м Виды и содержание учебных занятий

Вид материалаЛекции

Содержание


Промежуточный контроль знаний (Контрольная работа №1)
Промежуточный контроль знаний (Контрольная работа №2)
Подобный материал:

    Календарный план учебных занятий по дисциплине Компьютерный дизайн оптических наноструктур, НП-5м


    Виды и содержание учебных занятий

    Неделя
    Лекции
    Число часов
    Лабораторные занятия
    Число часов

    1, 2
    Методы оптимизации нулевого порядка, методы оптимизации первого, методы оптимизации второго порядков.

    4
    Построение целевой функции ошибок для градиентного метода для расчета отражающих решеток со ступенчатым профилем.
    4

    3
    Симплекс-метод Нелдера-Мида. Алгоритм Нелдера-Мида. Описание алгоритма. Свойства метода Нелдера-Мида.
    2
    Сдача лабораторной работы №1.
    2

    4, 5
    Оптимизация методом наименьших квадратов. Матрицы Якобиана и матрицы Гессе для задачи метода наименьших квадратов.
    4
    Построение целевой функции ошибок для градиентного метода для расчета диэлектрических бинарных решеток для ТM-поляризации.

    4

    6
    Метод Ньютона-Гаусса. Преимущества метода Ньютона-Гаусса. Реализация метода Ньютона-Гаусса.
    2
    Сдача лабораторной работы №2.
    2

    7
    Алгоритм Левенберга-Марквардта. Метод Левенберга-Марквардта как метод доверительных интервалов.
    2
    Анализ результатов лабораторных работ в рамках концепции вычислительного эксперимента.
    2

    8
    Промежуточный контроль знаний (Контрольная работа №1)
    2

    9, 10
    Проблема распространения волн в одномерных периодических средах. Постановка задачи. Задача о собственных решениях для электромагнитной волны (задача о собственных волнах) в среде с одномерной модуляцией .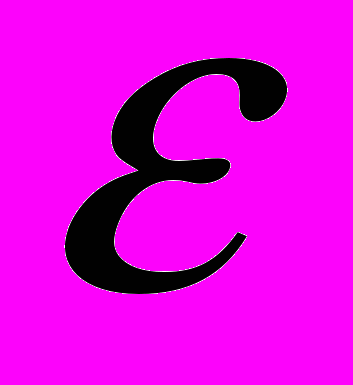
    4
    Построение целевой функции ошибок для градиентного метода для расчета диэлектрических бинарных решеток для ТЕ-поляризации.
    4

    11, 12
    Анализ дисперсионного уравнения. Обсуждение физического смысла решений. Условие Брэгга. Частотная и угловая полосы брэгговского отражения, пропорциональные глубине модуляции диэлектрической проницаемости.
    4
    Сдача лабораторной работы №3. Анализ результатов лабораторных работ в рамках концепции вычислительного эксперимента

    4

    13
    Амплитуды пространственных гармоник. Диэлектрическое зеркало.
    2
    Сдача лабораторной работы №4
    2

    14
    Диэлектрическое зеркало, основанное на эффекте брэгговского отражения. Зависимость коэффициента отражения и пропускания брэгговского зеркала от угла падения и частоты падающей плоской монохроматической волны.
    2
    Анализ результатов лабораторных работ в рамках концепции вычислительного эксперимента.
    2

    15
    Промежуточный контроль знаний (Контрольная работа №2)
    2

    16, 17
    Задача о синтезе оптических систем с заданными энергетическими коэффициентами пропускания и отражения. Физическое содержание рассматриваемой задачи синтеза. Задача синтеза в классе кусочно-постоянных функций, т. е. для слоистых систем. Математическая постановка задачи.
    4
    Задача оптимизации геометрических параметров брэгговского зеркала с целью максимизации коэффициента отражения.
    4

    18, 19
    Вычисление целевого функционала и градиента функционала для слоистых сред. Алгоритм минимизации функционала и некоторые результаты расчетов. Поиск локальных минимумов по обычному методу проекцией градиента.
    4
    Задача оптимизации геометрических параметров просветляющего покрытия с целью максимизации коэффициента пропускания.
    4

    20
    Итоговый контроль знаний
    2