Geum.ru

Использование Mathcad и Excel при изучении школьного курса физики

Вид материалаДокументы

Содержание


Применение электронных таблиц Excel при решении физических задач.
Подобный материал:
Использование Mathcad и Excel при изучении школьного курса физики

Semenenko M.G., Kondratieva S.D.

Рассматривается практика применения электронных таблиц Excel и пакета прикладных программ Mathcad для углубленного изучения школьного курса физики и подготовки к сдаче ЕГЭ.

We consider the practice of spreadsheets Excel and software package Mathcad for in-depth examination of school physics course and prepare for the delivery of Unified State Exam.

Введение. Внедрение информационных технологий в учебный процесс позволяет сделать более интенсивным и интересным изучение «классических» школьных дисциплин, что особенно актуально в связи с массовой компьютеризацией школ и повсеместным внедрением единого государственного экзамена (ЕГЭ). Классы учебного центра “Формула” г.Калуги, предназначенные для проведения занятий по различным обучающим курсам, оборудованы современными компьютерами. Поэтому мы провели эксперимент по использованию современного ПО в курсе углубленного изучения физики, включая подготовку к ЕГЭ. В данной статье приведены примеры применяемых нами методик на основе использования вычислительной системы Mathcad и электронных таблиц Excel.


Применение электронных таблиц Excel при решении физических задач. В современных условиях остро стоит вопрос о повышении качества и результативности обучения. В данном разделе приведен пример использования электронных таблиц при подготовке к решению задач ЕГЭ по физике. «Слабым местом» учащихся средней школы является решение задач, связанных с исследованием функций с помощью построения графиков. Таких задач достаточно много, хотя в школьном курсе часто им уделяется недостаточное внимание. Инструментом массового обучения школьников технологии решения подобных задач могут стать системы вычислительной математики, включая наиболее доступную и распространенную – электронные таблицы Excel.

Рассмотрим задачу, приведенную в [1].

При исследовании зависимости силы трения от силы давления были получены результаты, представленные на рисунке графиком (рис.1). Наиболее точно отражает результаты эксперимента зависимость:

1) Fтр = 0,3 Fд; 2) Fтр = 0,2 Fд; 3) Fтр = 0,1 Fд; 4) Fтр = 0,4 Fд .




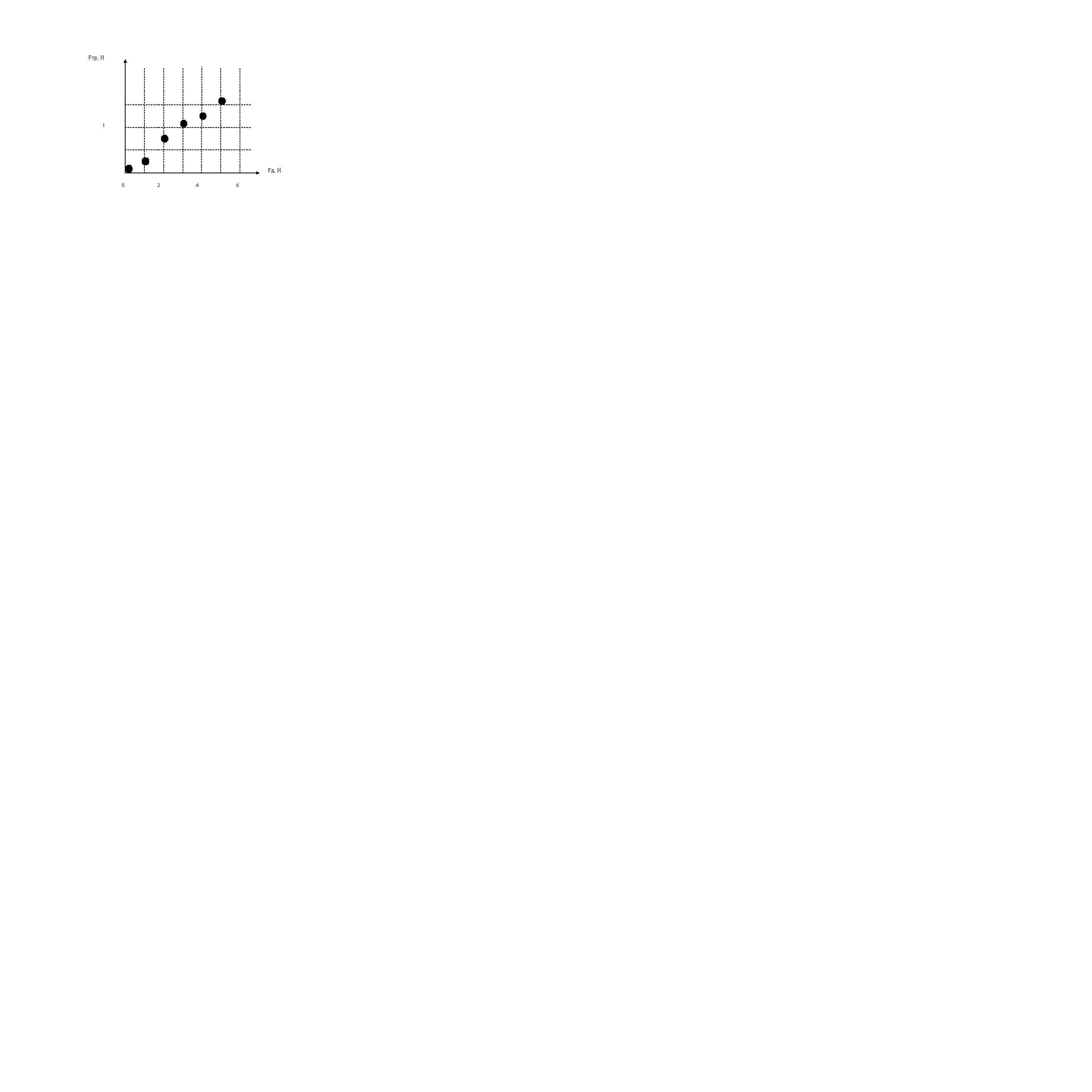
Рис. 1. Зависимость силы трения от силы давления


Чтобы лучше понять специфику задачи, построим указанный график, используя электронные таблицы Excel. Для этого занесем экспериментальные данные в соответствующую таблицу, построим график по экспериментальным точкам (опция Диаграмма|Точечная) и добавим график, соответствующий, например, значению k=Fтр/Fд, равному 0,2 (рис.2).

Из полученного рисунка видно, что практически все экспериментальные точки лежат над кривой теоретической зависимости, что говорит о «плохом» значении параметра k.

Изменяя значения k, получаем, что наилучший график соответствует k=0,3 (рис.3).

В процессе обучения школьники не только осваивали методику решения подобных задач, но и приобретали первоначальные навыки работы с электронными таблицами в объёме, достаточном для дальнейшего изучения и практического применения при дальнейшем обучении в ВУЗе. То же самое можно сказать и о решении задач с использованием пакета прикладных программ Mathcad.



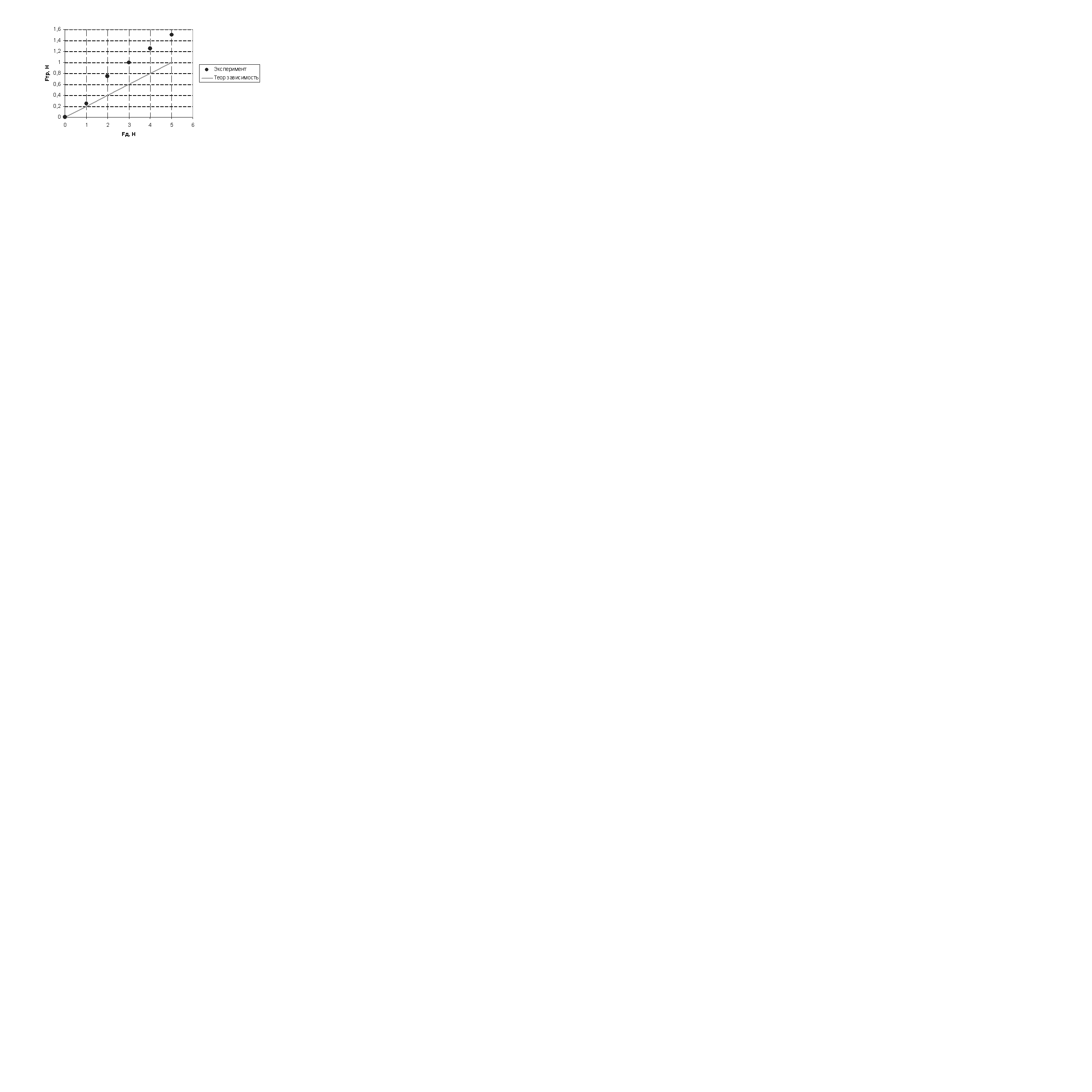
Рис. 2. График, соответствующий значению k =0,2



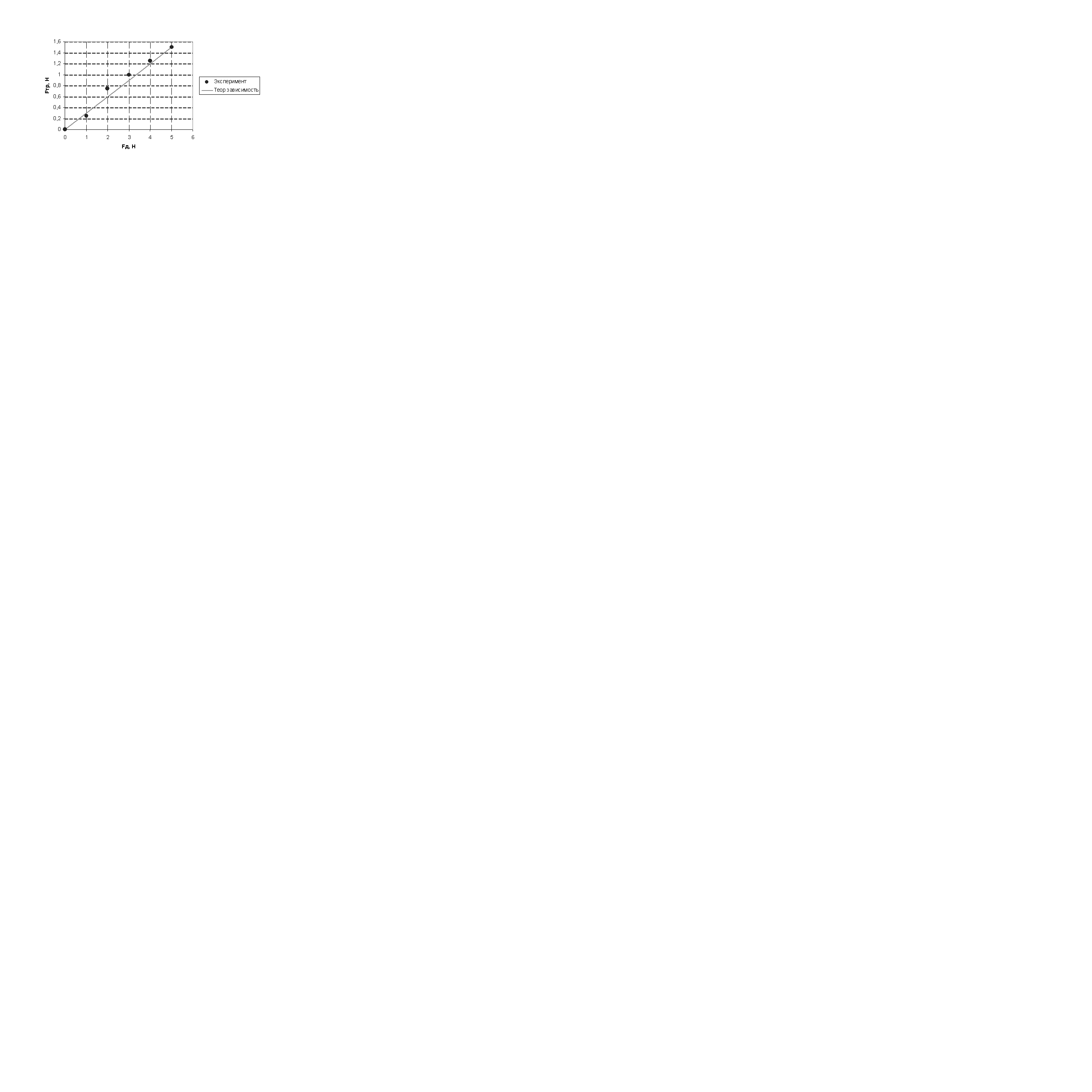
Рис. 3. График, соответствующий значению k =0,3


Применение вычислительной системы Mathcad для обучения решению физических задач. Перечислим основные особенности системы MathCad, которые делают ее наиболее удобной для решения физических задач школьного курса физики с использованием встроенных функций:
  • решение линейных и нелинейных уравнений и систем в численном и символьном виде, запись уравнений, близкая к «естественной»;
  • построение двумерных и трехмерных графиков, в том числе с использованием анимации; в частности, на экране компьютера легко получить визуализацию броуновского движения частицы (рис.4), а затем, нажимая клавиши Ctrl+F9, наблюдать различные варианты визуализации;
  • численное и символьное дифференцирование и интегрирование, символьное вычисление пределов;
  • поиск максимума и минимума (в том числе условного) функции.



Рис. 4. Броуновское движение одиночной частицы.


Для наглядности в файл MathCad можно вставлять рисунки, созданные в различных графических редакторах, а также текстовые комментарии.

В качестве примера рассмотрим решение следующей задачи [2].

С высоты H = 30 м свободно падает стальной шарик. Через t = 2 с после начала падения он сталкивается с неподвижной плитой, плоскость которой наклонена под углом 30 к горизонту. На какую высоту h над поверхностью Земли поднимется шарик после удара? Удар шарика о плиту можно считать абсолютно упругим.

Решение задачи проводится в два этапа (рис. 5). Сначала в символьном виде решается соответствующая система уравнений кинематики движения шарика после удара о плиту как движения тела, брошенного под углом к горизонту. Решение этой задачи в символьном виде легко получить с помощью функции Find (высота подъема шарика после удара относительно линии, показанной штриховкой, обозначена через h1). Затем вычисляется путь, пройденный шариком до удара, и высота H1 от места удара о плиту до поверхности Земли. Окончательно искомая высота h рассчитывается как сумма высот h1 и H1.

Наиболее сложные задачи решались стандартным образом («вручную»), а затем повторно с помощью компьютера.

В заключение отметим, что еще более впечатляющих результатов можно добиться, применяя пакеты прикладных программ при обучении студентов. Современные системы вычислительной математики позволяют по-новому взглянуть на организацию научных исследований и образовательного процесса. В частности, в последнее десятилетие возникла уникальная ситуация, когда при чтении научной статьи или книги можно в течение нескольких минут воспроизводить полученные в ней результаты на экране своего персонального компьютера. Этот факт создает основу для создания «виртуального физического практикума», когда студенты классических университетов и специальностей, связанных с высокими технологиями, могут обучаться на последних научных достижениях, изложенных в оригинальных статьях.

В частности, при моделировании динамики странного аттрактора в осцилляторах Дуффинга, на которые действует периодическая сила [3], при определенных значениях параметров можно видеть, что траектории в пространстве 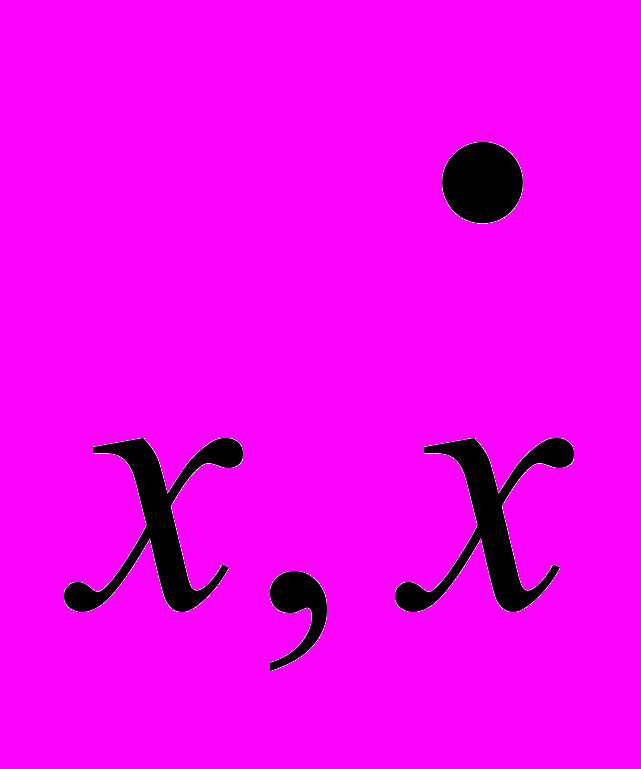сходятся к одной из неподвижных точек системы (рис.6). Рассматриваемая система описывается уравнением вида


.


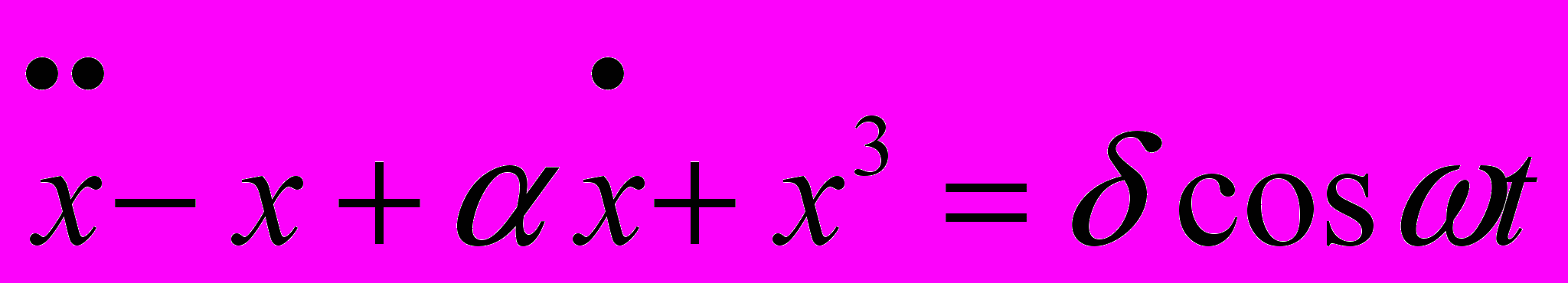Подобное уравнение возникает, например, в теории электрических цепей [4]. Соответствующая система дифференциальных уравнений является жесткой, поэтому стандартными методами (например, методом Рунге-Кутты) решить ее невозможно. В то же время в MathCad данная система легко решается с помощью опции Rkadapt, хотя еще недавно решение жестких систем дифференциальных уравнений представляло собой достаточно нетривиальную задачу.

Еще раз отметим, что рис. 6 идентичен аналогичному рисунку в оригинальной статье [3] и может быть получен на экране персонального компьютера в течение несколько минут.



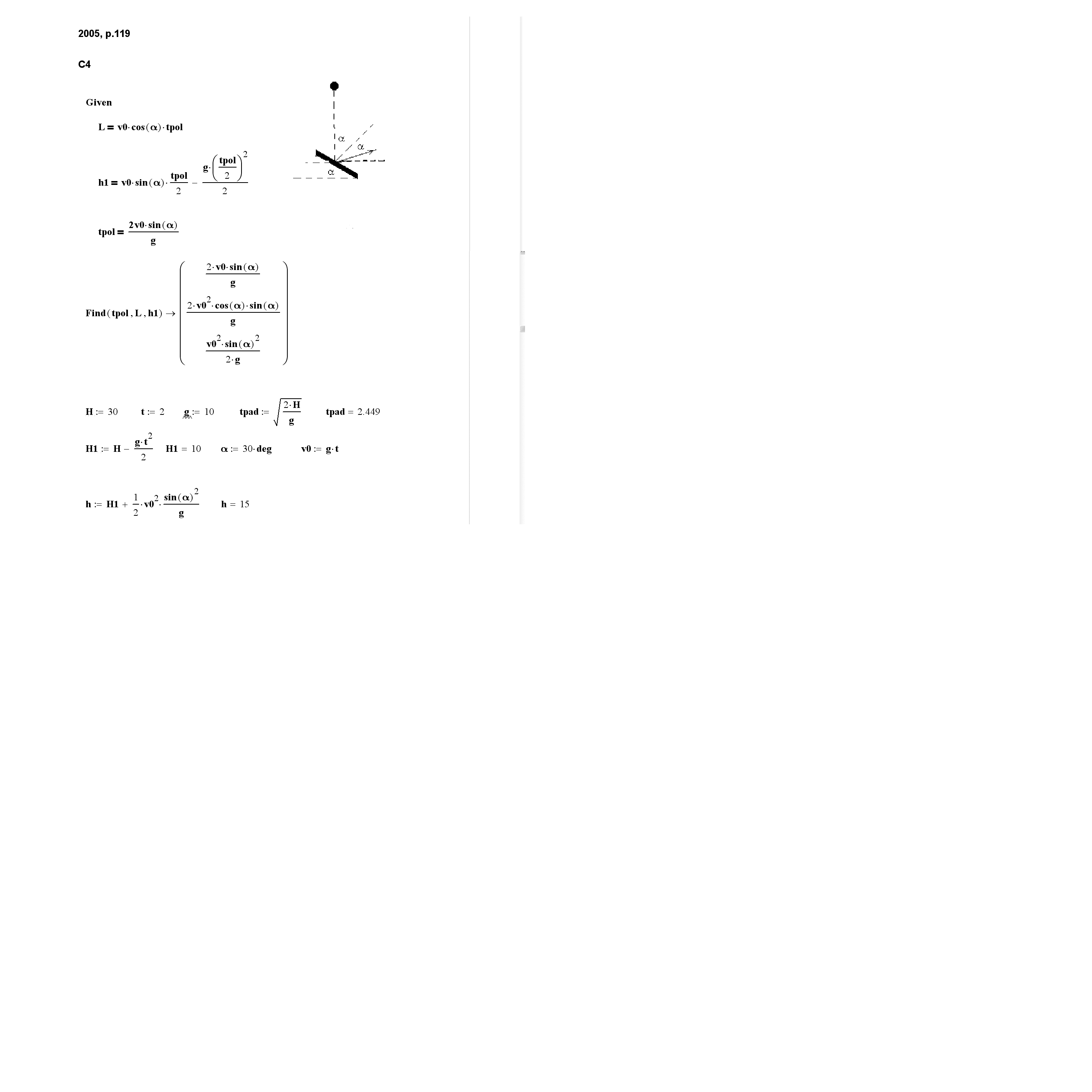
Рис. 5. Пример решения задачи в Mathcad



Рис. 6. Пример карты Пуанкаре для странного аттрактора

Литература
  1. Единый государственный экзамен: Физика: Контр. измерит. материалы/Под ред. Г.С.Ковалевой. – М.: Просвещение, 2003. с.30.
  2. Единый государственный экзамен: Физика: 2004 - 2005. Контр. измерит. материалы/Под ред. Г.С.Ковалевой. – М.: Просвещение, 2005. с.119.
  3. G.M. Mahmoud, A.M. Mohamed, S.A.Aly// Physica A, v.292, 2001, p.193.
  4. C.Hayashi. Nonlinear Oscillators in Physical Systems. – NY: McGraw-Hill, 1964.