Использование электронных таблиц при изучении темы «Логика»

Вид материала

Программа

Содержание Вид – Панели инструментов – Формы – Выбрать флажок. A(a+b); a&b=a&b+b&b=b(a+b) S= abp+abp+abp+ab

Подобный материал:

• Темы курсовых работ по методике преподавания информатики на 2006-2007 уч год, 16.24kb.
• Использование Mathcad и Excel при изучении школьного курса физики, 67.71kb.
• «Использование электронных таблиц Microsoft Excel для компьютерного тестирования», 222.92kb.
• Программа ms excel входит в пакет Microsoft Office и предназначена для подготовки, 127.81kb.
• Редакторы электронных таблиц, 407.79kb.
• Положение о Фестивале инновационных проектов 4 Использование схем и таблиц при изучении, 546.25kb.
• Н. Ю. Использование компонентов медиаобразования при изучении квантовой физики. Автореф, 310.43kb.
• Программа курса и темы практических занятий; Логика в таблицах и схемах. Логика как, 1722.34kb.
• Курсовая работа Использование цор при изучении темы «Предел последовательности» в шкм, 214.29kb.
• Конспект урока по биологии 11 класс, 86.13kb.

Использование электронных таблиц при изучении темы «Логика»

В Стандартах и Примерных программах включены всевозможные вопросы математической логики, но ни логические элементы ни логические схемы не упоминаются ниже уровня «процессор - память – устройства ввода/вывода», но в рекомендованных Министерством образования билетах выпускного экзамена по информатике сформулирован вопрос «Логические элементы и схемы. Типовые логические устройства компьютера: полусумматор, сумматор, триггеры, регистры». Кроме того при изучении темы «Основы логики и логические основы компьютера» отсутствует компьютерная реализация базовых понятий логики: таблиц истинности, логических функций, элементов и схем. Учитель стоит перед выбором: как проводить занятия, чтобы повысить познавательный интерес, связать данную тему с теоретическим курсом «Информатика», практикой, обеспечить проверку усвоения полученных знаний, не имея достаточного программного обеспечения. В создавшейся ситуации считаю возможным и эффективным применять при изучении этой темы электронные таблицы Excel.

Наличие функционального полного набора логических функций (И, ИЛИ, НЕ) в программе Еxcel помогает учащимся не только освоить эту тему, но и самостоятельно строить таблицы истинности. При объяснении темы «Логических функции» обучающиеся имеют возможность самостоятельно, воспользовавшись встроенными логическими функциями ЭТ проверить эти таблицы и построить соответствующие логические схемы.

Например: Построить таблицу истинности дизъюнкции.

Просматриваем всевозможные комбинации для двух переменных. В одну из ячеек вводим значение ЛОЖЬ, в соседнюю ЛОЖЬ, в следующую вставляем функцию (Вставка – Функция – Логические – ИЛИ), выбираем ячейки с введенными значениями, получаем результат. Копируем формулу. В Excel результат логической операции отображается словами ИСТИНА или ЛОЖЬ. Можно представить результат в виде значений 0 и 1, термины истина и ложь скрыты в столбце К электронных таблиц, а для наглядности в столбце J помещена функция ЕСЛИ ( если(Е5=истина;1;0 )), при этом цвет шрифта в ячейке со словом ИСТИНА сделан белым или в цвет фона таблицы.

При изучении этой темы в профильном классе, где времени достаточно, можно моделировать работу базовых логические элементов, а также полусумматора и сумматора.

1. Нарисовать схему.
   
2. На входы поставить флажок: Вид – Панели инструментов – Формы – Выбрать флажок. Связать с ячейкой для записи результата: правой кнопкой мыши –Формат объекта – Элемент управления или в горизонтальном меню – Формат – Элемент управления – связать с - выделить ячейку для записи результата, например В4.
   

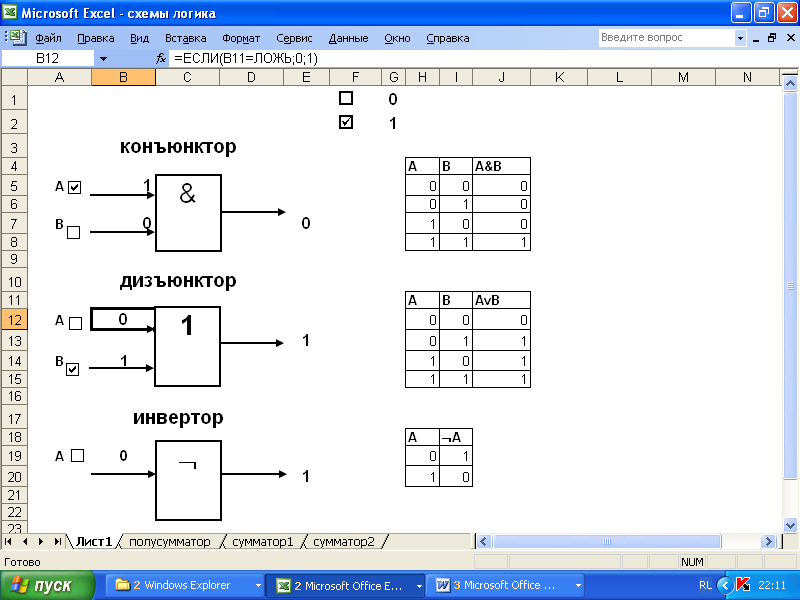
Рис. 1

Сумматор является центральным узлом арифметико-логического устройства компьютера. Одноразрядный сумматор на два входа и два выхода называется одноразрядным полусумматором. Обозначим слагаемые А, B, перенос Р и сумму S.

Для построения полусумматора необходимы знания законов логики, умений построения таблиц истинности и получения логического выражения по таблице истинности.

Получение логического выражения по таблице истинности:

1. выбрать значения переменных, для которых значение функции равно1;
   
2. записать логическое умножение всех переменных для каждой строки, где F=1 (если значение переменной равно 0, то берется её отрицание);
   
3. логически сложить полученные выражения;
   
4. упростить полученное выражение.
   

Используя правила сложения в двоичной системе счисления, построим таблицу истинности (рис. 2). Составим формулы работы сумматора:

Р=А&В, S=A&B+A&B. Упростим полученную формулу

A&B=A&B+A&A=A(B+A)=  A(A+B); A&B=A&B+B&B=B(A+B);

S=A&B+A&B=A(A+B)+ B(A+B)= (A+B)( A+B)= (A+B)&(A&B). (формула 1)

Построим логическую схему простейшего одноразрядного двоичного сумматора на два входа и два выхода:




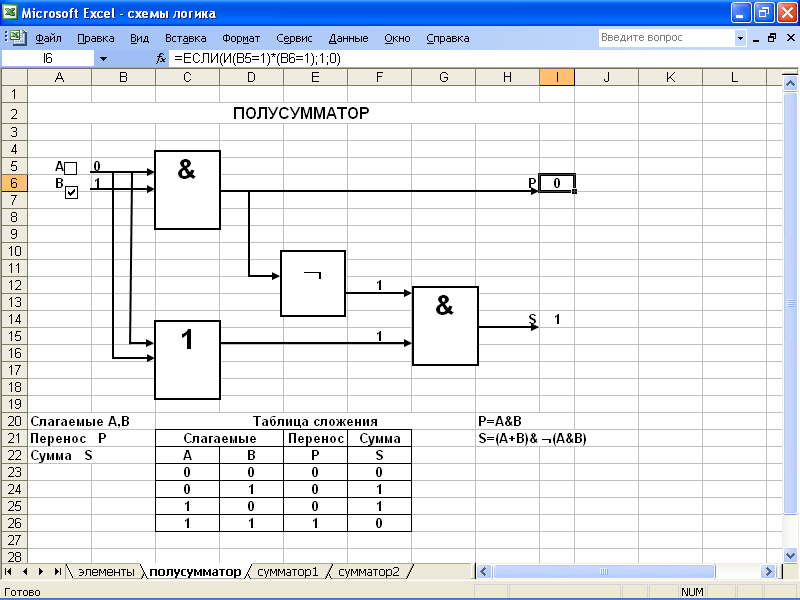
Рис.2


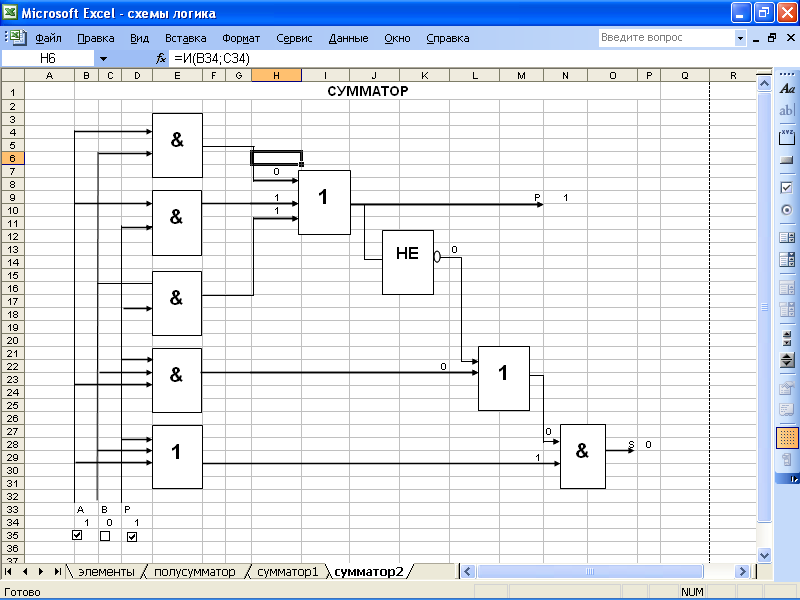
Полный одноразрядный сумматор на три входа и два выхода называется полным одноразрядным сумматором

Работа одноразрядного двоичного сумматора может быть описана таблицей (рис.3).

По таблице истинности составим формулу: S=A&B&P₀+A&B&P₀+A&B&P₀+A&B&P₀; Р принимает значение 1, когда хотя бы два входных значения одновременно равны 1.

P=A&B+A&P₀+B8P₀. После преобразования получим формулу, по которой строится схема. S=((A&B+A&P₀+B&P₀)+A&B&P₀)&(A+B+P₀);

Вывод формулы: для простоты записи обозначим P₀ – P, знак & - *

S= ABP+ABP+ABP+AB₀=P(AВ+AВ)+P( AВ+AВ) (применим формулу1) = P((A+В)*(AВ))+P( A*В+A*В) (применим закон де Моргана) = P((A+В)*(AВ))+P( (A+В)+A*В)

Обозначим Х=(A+В)*(AВ), Х=((A+В)*(AВ))= (A+В)+AВ)

S=P*X+P*X=(ф1)=(P+X)* (P*X)= (P+X) *(P+X) (ф.2).

P+X =P+(A+В)*(AВ)=(дистрибутивный закон логики)= (P+(A+В))*(P+(AВ)) вернемся к ф.2

S=(P+A+В))*(P+(AВ))*(P+(A+В)+A*В)=(ф.3)(выполним умножение 2 и 3 скобки) (P+(AВ))*(P+A*В+A*В)=

=0+P*A*B+P*A*B+P*(A*B)+ (A*B)* A*B+0= P*A*B+P*A*B+P*(A+B)+( A+B)* A*B= P*A*B+P*A*B+P*A+P*B+A*B+A*B= A*B*P+A*B(1+P)+A*P+B*P= A*B*P+A*B+A*P+B*P= A*B*P+( (A+B)+(A+P)+(B+P))= A*B*P+ ((A+B)*(A+P)*(B+P))=(выполним умножение)=A*B*P+ ((A+A*P+A*B+B*P)*(B+P))= A*B*P+(A*(1+P+B)+B*P)*(B+P))= A*B*P+((A+B*P)*(B+P))= A*B*P+(A*B+A*P+B*P)=(подставим в ф.3)

S=(A+B+P₀)*((A*B+A*P₀+B*P₀)+A*B*P₀);




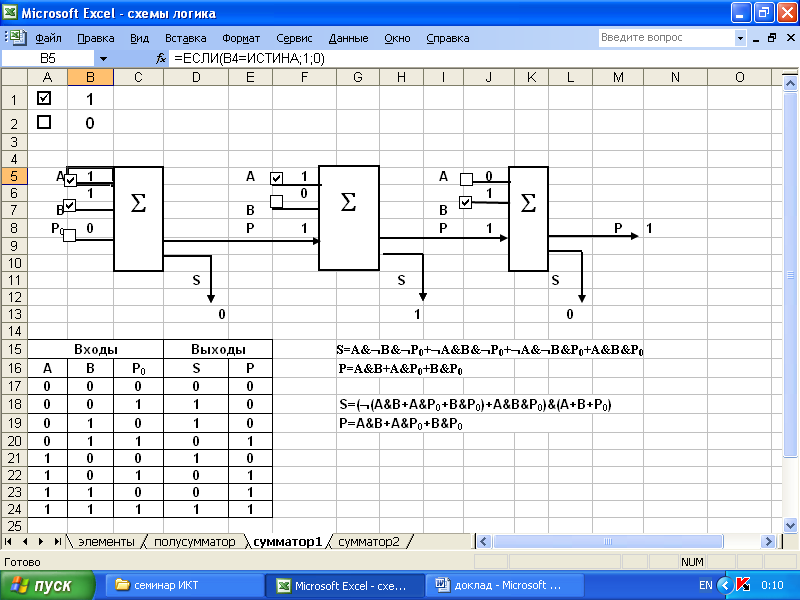
Рис.3





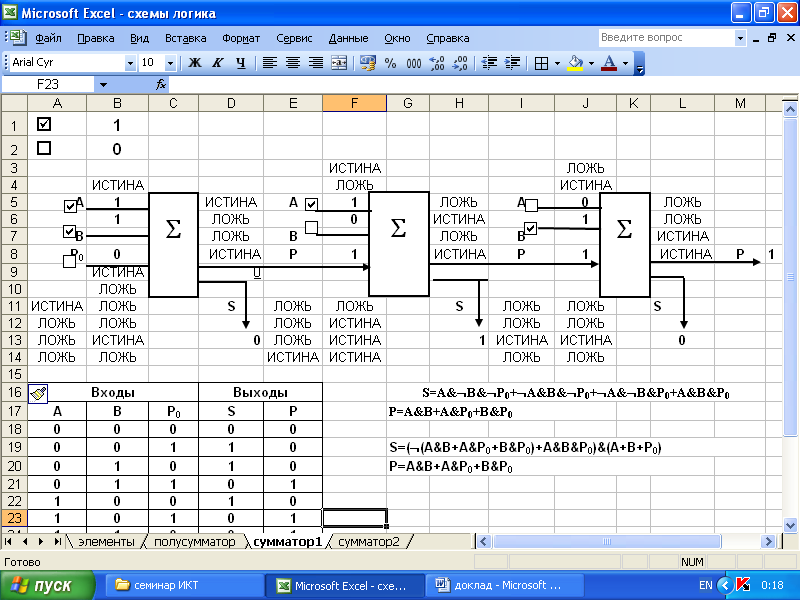
Для построения сумматора необходимо девять базовых логических схем




При изучении темы «Логика», ребята задают вопрос «Зачем все это нужно? Конъюнкция, дизъюнкция, таблицы истинности и т.д.» Построение узлов компьютера с помощью таблиц Excel «своими руками» создает у учащихся единую связанную картину изучаемого материала. Разрозненные абстрактные знания о логических функциях оказываются непосредственно связанными с устройством реального компьютера. По моему мнению степень усвоения материала по теме «Логика» стала гораздо выше.

Литература: Кутугина Е.С. Учебное пособие. Томск: ТУСУР, 2004

Иванова И.А. Информатика.10 класс: Практикум. – Саратов: Лицей, 2004.

Е.А.Еремин Информатика №12,13 Издательский дом «Первое сентября»