Курсовая работа Использование цор при изучении темы «Предел последовательности» в шкм
| Вид материала | Курсовая |
СодержаниеХод урока Последовательность (x Показать парадокс Стоп приостанавливает анимацию, кнопка Сброс |
- Использование электронных таблиц при изучении темы «Логика», 57.48kb.
- Курсовая работа по управлению судном, 128.72kb.
- Программа вступительных испытаний в магистратуру по направлению 010200. 68 Математика., 1967.42kb.
- Задача Вычислить предел последовательности, 34.49kb.
- Темы курсовых работ Вариант 1: буквы а-б-в курсовая работа по теме: Формирование, 115.39kb.
- Н. Ю. Использование компонентов медиаобразования при изучении квантовой физики. Автореф, 310.43kb.
- Курсовая работа на тему: тема: "Метод глубинного интервью при изучении криминальной, 511.8kb.
- Курсовая работа на тему: Использование мультимедийного контента при разработке приложений, 310.8kb.
- Урока по литературе с использованием цор. 8 класс. Тема урока: Создание электронной, 75.82kb.
- Самостоятельная работа, ее роль в изучении физики. 15. Требования к оснащению учебного, 170.13kb.
Федеральное Агентство По Образованию Государственное Образовательное Учреждение Высшего
Профессионального Образования Красноярский Государственный Педагогический университет
им. В.П. Астафьева
(ФАПО ГОУВПО КГПУ им.В.П.Астафьева)
математический факультет кафедра математического анализа и методики его преподавания
Курсовая работа
Использование ЦОР при изучении темы «Предел последовательности» в ШКМ.
Выполнила студентка 42 группы математического факультета Лекарева Е.А
Проверила доцент кафедры математического анализа и методики его преподавания, к.ф.- м.н. Якименко М.Ш.
Красноярск. 2007
Содержание
- Введение 3
- Конспект урока 4
- Методические рекомендации 13
4. Обоснование выбора цифровых образовательных ресурсов (ЦОР)... 17
- Заключение 18
- Библиографический список 19
Введение
Современный этап развития российского образования характеризуется широким внедрением в учебный процесс компьютерных технологий. Они позволяют выйти на новый уровень обучения, открывают ранее недоступные возможности, как для учителя, так и для учащегося. Использование ЦОР на уроках помогает лучшему усвоению как отдельных тем, так и изучаемых дисциплин в целом. Уроки с использованием компьютера, проводятся наряду с обычными занятиями, где возможно и целесообразно использование компьютеров для решения частных задач урока, чтобы ученик глубже понял, почувствовал тему урока, творчески проявил себя. Использование компьютера при обучении позволяет создать информационную обстановку, стимулирующую интерес и пытливость учащегося.
Данная тема «Предел последовательности» изучается в курсе Алгебры и начала анализа в 10 классе, в главе 4 «Производная» по учебнику Мордкович А.Г «Алгебра и начала анализа 10-11 »; Соответственно изучается перед введением понятия производной функции. На изучение темы «Предел последовательности» отводится 2 часа. Теория пределов - достаточно сложный раздел математического анализа. Поэтому в школе знакомство с понятием предела поверхностное, основанное на интуиции и наглядных представлений.
Использование возможностей компьютера позволяет обеспечить более полное представление понятия предела на интуитивном уровне. Занятия на компьютерах позволяют частично разрядить эмоциональную напряженность и создать более благоприятный климат на уроках. Большая часть знаний, умений и навыков (ЗУН), полученных на традиционных уроках, не используется учащимися во внеурочной деятельности, и их практическая ценность утрачивается, а прочность - существенно снижается. Использование же ЗУН в компьютерной среде приводит к их актуализации, а интерес работы за компьютером - к мотивации их приобретения.
Вводная лекция по теме «Предел последовательности»
Цели
- Дать на интуитивном уровне полное представление о понятии
«Предел последовательности»;
- Формирование у учащихся понятия «Предел последовательности»;
- Формирование представлений о Математике как универсальном языке
науки; средстве моделирования явлений и процессов;
- Развивать элементы логического мышление, умение делать вывод;
- Развивать любознательность у учащихся;
- Развивать познавательный интерес у учащихся;
- Воспитать средствами математики культуры личности через
знакомство с историей развития понятия «Предел
последовательности».
8. Развитие у учащихся элементов способности видеть и использовать в учебной деятельности межпредметные связи, знания других наук.
Структура урока
- Организационный момент 3
- Историческая правка 11
- Об интуитивном понятии «Предел последовательности» 7
- Формулировка математического определения 9
- Объяснение парадокса «Ахиллес и черепаха» 7
- Итог урока 3
Оборудование: проектор, компьютеры с установленной программой «Открытая математика 2.5.Функции и графики».
ХОД УРОКА
1. Организационный момент
Здравствуйте. На прошлом уроке мы познакомились с числовыми последовательностями. И сейчас повторим, что мы называем числовой последовательностью. (Числовой последовательностью называется числовая функция от натурального аргумента) Хорошо, вспомнили.
А на сегодняшнем уроке, нам предстоит, познакомится с пределом числовой последовательности. И сейчас просмотрим план, по которому мы будем работать (электронное приложение 1,слайды 1 и 2)
2. Историческая справка
Начнем работу с первого пункта. Я расскажу Вам небольшой очерк из истории возникновения теории пределов (электронное приложение 1, слайды с 3-11)
( Всё ученикам записывать не нужно, ученики записывают то что просит учитель. Причем учитель сам диктует то, что надо записать.)
Первый факт из будущей Теории Пределов нечаянно открыли древние египтяне. Еще в эпоху постройки пирамид архитектор Имхотеп задался простым вопросом: что получится, если к единице прибавить ее половину, и еще половину ее половины, и еще... и так далее, без конца? Ясно, что такая процедура потребует бесконечного времени - так что точный ответ знают только боги. И их жрецы! Имхотеп был верховным жрецом бога Тота и имел право говорить от его имени. Когда жрец заявил, что бесконечная сумма, заданная выше, равна числу 2 - никто не стал с ним спорить. Так египетский мудрец впервые преодолел свой страх перед бесконечностью и подал пример следующим дерзким мыслителям на все времена. Тот же Имхотеп сумел вычислить сумму бесконечно убывающей геометрической прогрессии с любым знаменателем. Но рассчитать объем пирамиды с помощью
предельного перехода - этот подвиг совершили только хитроумные афиняне
в Академии Платона (4 век до н.э.).
Решающий шаг к этой победе сделал Евдокс, приезжий из города Книда. Он
жил в афинской гавани - Пире, и каждое утро шел в Академию (около 8 км),
размышляя по дороге над очередной задачей. Как-то раз он вспомнил, что
египетские пирамиды составлены из кубических блоков известняка: оттого
их объем не трудно рассчитать, зная объемы кубиков. Конечно, в этом
расчете есть погрешность - но ею можно пренебречь, ведь кубики совсем
малы, в сравнении с пирамидой! Главное - понять, насколько число кубиков
в каждом слое больше, чем в другом слое лежащем на один ряд выше. Вскоре
Евдокс заметил, что объемы последовательных слоев различаются на один
ряд кубиков. То есть, для вычисления объема одного слоя кубиков нужно
будет суммировать арифметическую прогрессию объемов: это дело
привычное! Для нахождения объема всей пирамиды суммирование нужно
повторить дважды. Во второй раз придется суммировать квадраты чисел:
1 + 4 + 9 +...+ n2 Евдоксу удалось вычислить эту сумму: она равна
, или примерно n3. Вот откуда берется загадочный множитель в той формуле объема пирамиды, которую угадали из опыта еще древние египтяне!
Через полвека открытия Евдокса попали в книгу Евклида «Начала» («Стойхейя»): она на много веков стала лучшим учебником геометрии для любознательных студентов. Через сто лет после Евклида Архимед научился строго вычислять объемы не только пирамид и конусов, но также шара и его частей - все это с помощью предельного перехода. Вскоре после этого Архимед погиб при взятии Сиракуз римлянами, которые боролись с Ганнибалом (212 год до н.э.). Затем развитие греческой науки вообще остановилось - ввиду подчинения Эллады римлянами и последующего упадка Римской империи.
Новая революция в теории пределов произошла в 17 веке, когда Кеплер и Ньютон перенесли понятие предела с числовых последовательностей на числовые функции и их графики.
Первый строгий и понятный учебник по этой науке появился в начале 19 века в Париже. Там Огюстен Луи Коши прочел для студентов Политехнической школы первый курс, где понятия «предел функции в точке», «сходящийся ряд», «интеграл функции на отрезке» были определены с полной строгостью - так, что по этим определениям можно вести вычисления пределов последовательностей, производных и интегралов функций, сумм рядов и иных объектов Анализа.
После трудов Коши Анализ Функций стал доступен даже школьникам старших классов. Но массовое введение этой науки в школьную программу заняло более ста лет. В России производные и интегралы стали общим достоянием школьников в 1970-е годы, благодаря усилиям А.Н.Колмогорова и его учеников.
3.06 интуитивном понятии предела последовательности ( электронное
приложение 1, слайды с 12-17)
Как многие из Вас поняли понятие «Предел последовательности» является формализацией интуитивного понятия «стремления», «неограниченного приближения». Проследим это на примерах, (слайды 12-14)
Пример 1. Рассмотрим последовательность выбиваемых очков при стрельбе по мишени.
Если хороший стрелок «пристреливает» оружие: т. е для любого круга с центром в «пятерке» найдется номер, начиная с которого, все пули укладываются в этой круг.
Тогда можно сказать, что «Предел» этой последовательности является 5 очков.
Пример 2. Бросим на пол теннисный шарик и будем фиксировать максимальную высоту отскока. Допустим, что первый раз шарик подскочил на 1 метр, второй - на Уг, третий - на 1/3 и т.д. если этот процесс происходит в реальности, то шарик, в конце концов, остановится. Но если рассматривать математическую модель, то можно считать, что шарик продолжит отскакивать сколь угодно долго и высота отскока n-го отскока равна 1/п метра.
В этой моделе процесс описывается с помощью бесконечной последовательности чисел 1,1/2,1/3,... причем с увеличением номера п дробь 1/п уменьшается, приближаясь к нулю:
¼>0.001 при п> 1000
1/п<10-6прип>106
Говорят, что число 0 является пределом числовой последовательности 1/п при п стремящемся к бесконечности и записывается следующим образом
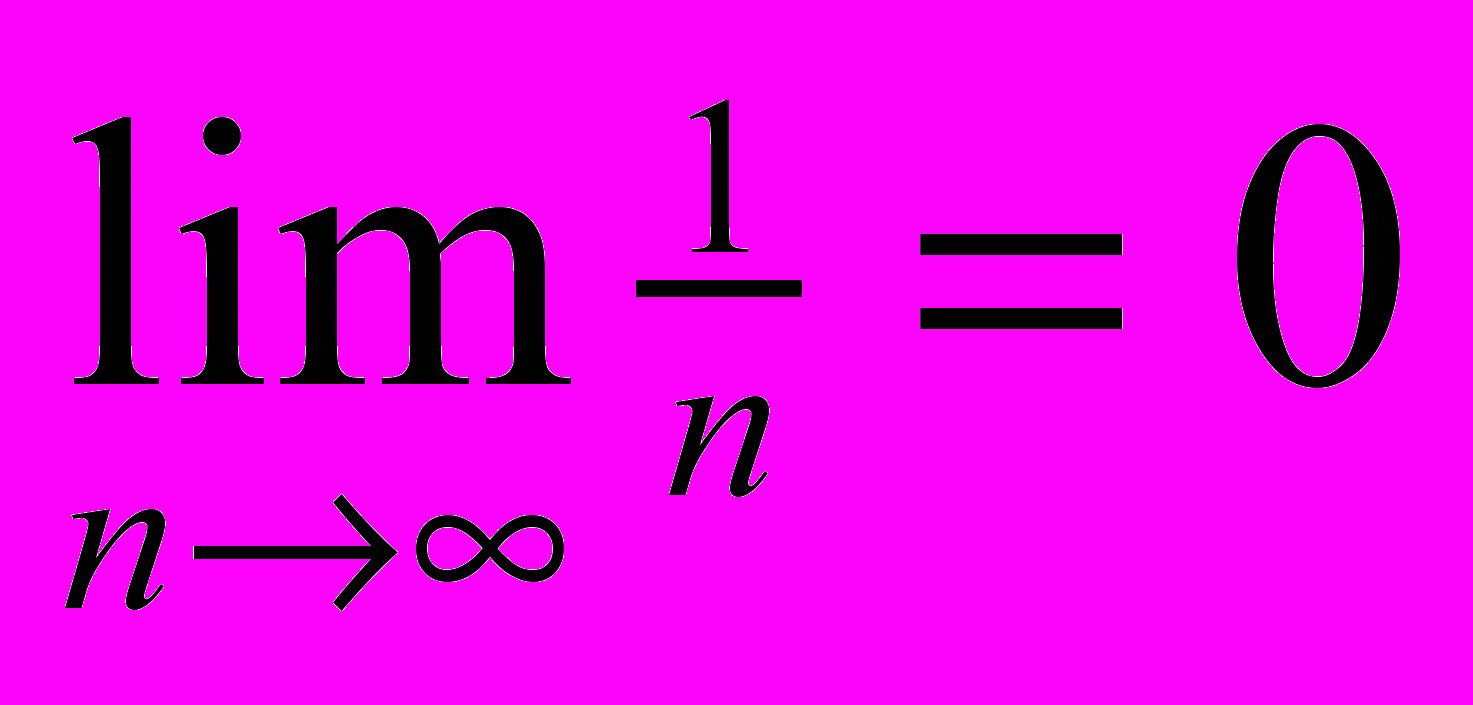 ..(1)
..(1)Знак lim есть сокращение от латинского слова «limes», т.е граница. Формулу (1) читают так: предел последовательности при п стремящемся к бесконечности дроби 1/n равен 0.
3. Формулировка математического определения ( электронное
приложение 1, слайды с 18-22)
Математика - как известно точная наука. Поэтому при дальнейшем изучении математики знания интуитивного понятия предела последовательности будет недостаточно. Необходимо сформулировать точное математическое определение. Для этого рассаживаемся за компьютеры и выполняйте работу, которую я буду говорить.
Рассмотрим две числовые последовательности (X n) , (Y п). Теперь в
программе Графер, которая у Вас открыта, изобразите члены этих
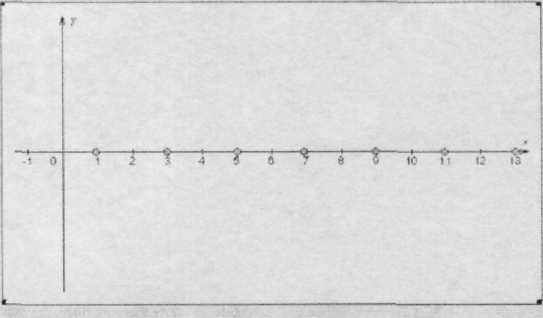
рис.1
последовательностей точками на координатной прямой.. У Вас должно получиться следующее..
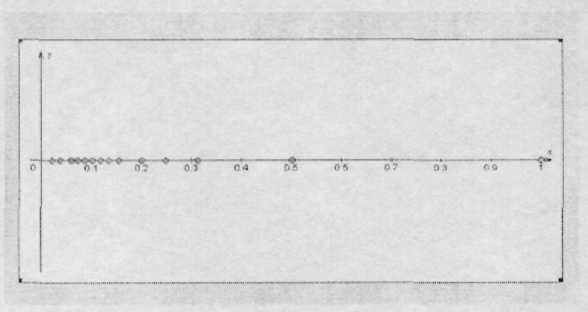
рис. 2
(далее следуют вопросы ученикам).
1.Что можно заметить о точках, соответствующих членам последовательности (Yn)?.; возле какой точки они как бы «сгущаются»
(возле точки 0)
2. Что можно заметить о точках, соответствующих членам последовательности (X n)? (такой точки сгущения нет) В подобных случаях математики говорят так:
ПОСЛЕДОВАТЕЛЬНОСТЬ (Xn)
РАССХОДИТСЯ ПОСЛЕДОВАТЕЛЬНОСТЬ (Yn) СХОДИТСЯ.
Возникает естественный вопрос: как знать, является ли конкретная точка, взятая на прямой, «точкой сгущения» для членов заданной последовательности. Чтобы ответить на этот вопрос введем новый математический термин
Определение 1.
Пусть а - точка прямой, а r - положительное число.
Интервал (а-п а+r) называют окрестностью точки а, а число r - радиусом окрестности
Рассмотрим еще примеры
1.(5,98:6.02) - окрестность точки 6 и радиусом г=0,02 2.(2,36:3.64)-окрестность точки 3 и радиусом г=0,64
Теперь мы можем ответить на поставленный вопрос. Но уточню: математики
не любят термин «точка сгущения» для членов заданной последовательности,
они предпочитают термин «Предел последовательности». Запишем
определение в тетрадь.
Определение 2.
Число b называют Пределом Последовательности (Y п) . если в любой
заранее выбранной окрестности точки b содержаться все члены последовательности, начиная с некоторого номера
4. Объяснение парадокса «Ахиллес и черепаха» ( электронное приложение 1 слайды 23 и 24)

Сейчас снова поработаем за
компьютерами. Перед Вами
интерактивная модель. которая демонстрирует знаменитый парадокс древнегреческих мудрецов «Ахиллес и черепаха». В одной из современных
формулировок он выглядит так. Пусть Ахиллес бежит в десять раз быстрее,
10
чем черепаха, и находится от нее на расстоянии в 100 метров. За то время, за которое Ахиллес пробежит 100 метров, черепаха проползет 10 метров. Когда Ахиллес пробежит 10 метров, черепаха проползет 1 метр, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес никогда не догонит черепаху. Осуществим парадокс и просмотрим, как он работает. Как вы можете объяснить, на интуитивном уровне результат парадокса?
Ученики рассуждают на интуитивном уровне о результате. После обсуждения, учитель рассказывает систему парадокса на научном языке, с помощью понятие предела.
Зенон Элейский в одном из своих парадоксов утверждал, что быстроногий Ахиллес никогда не догонит черепаху. Действительно, рассуждает философ, пока Ахиллес добежит до того места, где была черепаха, она уже окажется в другом месте. Когда Ахиллес прибежит на это место, черепаха уже отползет дальше и т. д.
Получившиеся точки образуют последовательность:

Рассмотрим парадокс Зенона более подробно (уже опираясь на введенное понятие предела). Предположим, что Ахиллес и черепаха- это точки, движущиеся по прямой с постоянными скоростями, причем скорость Ахиллеса в 10 раз больше скорости черепахи, а начальное расстояние между ними- 10 метров. Пока Ахиллес пробежит это расстояние, черепаха отползет на 10 метров, т. е расстояние между ними уменьшится в 10 раз. Далее, когда Ахиллес пробежит 10 метров, отделяющие его от черепахи, она отползет еще на 1 метр и т. д. Изобразим промежуточные старты Ахиллеса точками на числовой оси...
S, =100, S2=100+10=110, S3=100+10+l = l 11, S4=100+10+l+0.1 = 111.1 ит.д Ясно, что они скапливаются около точки, координатой которой является периодическая дробь S=100+10+l+0,l+...+..= l 11,(1 )=111 1/9 - это число является пределом последовательности S| . S2, S3, S4 ,... что записывается следующим образом
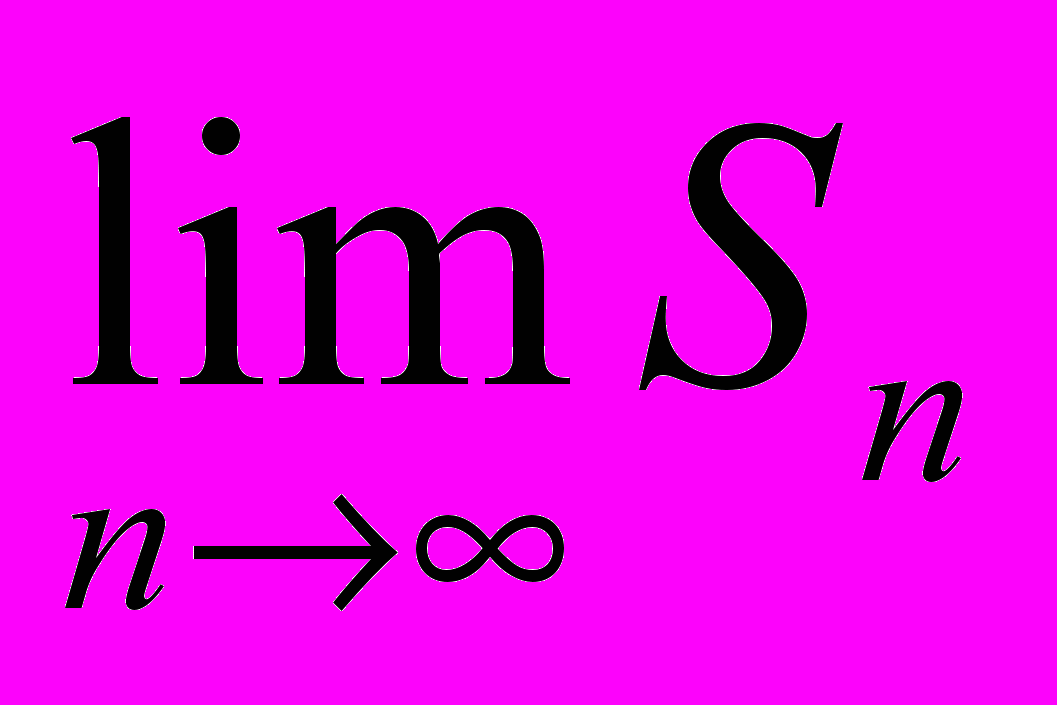 = 111 1/9.
= 111 1/9. именно в точке с координатой 111 1/9 Ахиллес догонит черепаху.
Проблему, которую поставил Зенон в этом парадоксе носит философский характер и связана не столько с обсуждением характера движения, сколько с более общими вопросами: что такое время, что такое непрерывность, можно ли придумать механизм, реализующий за конечное время бесконечное число процедур и т. д.
5. Итог урока
На этом мы закончим вводную лекцию. Мы хорошо поработали. И из истории послушали интересные факты о теории пределов. На интуитивном уровне поработали с понятием «предел последовательности», сформулировали строго математическое определение и в заключении рассмотрели древний парадокс. На следующем уроке мы уже приступим рассмотрению темы «Предел функции в точке, предел функции на бесконечности», «Вычисление пределов», «Теоремы о сумме, произведения, частного пределов»
У кого возникли трудности в процессе работы, кому, что осталось не понятным? (идет обсуждение ответов)
Кому понравилось работать за компьютерами или кто утомился за работой на компьютере? Может кому то трудно было воспринимать информацию с проектора?
12
Методические рекомендации по изучению вводной лекции на тему «Предел последовательности» на основе использования ЦОР
Место данной темы в Школьном курсе Математики: Согласно программе по Математике в базовой школе формирования понятия предела функции рассматривается на интуитивном уровне и используется для формирования понятия производной. Соответственно изучается перед введением понятия производной функции. На изучение темы «Предел последовательности» отводится 2 часа
Понятиями, которыми должны владеть учащиеся для проведения этого урока: числовая последовательность, способы задания, ограниченная последовательность, монотонная последовательность
Работа за компьютерами рассчитана согласно СанЭпиНад не более 20 минут
| Этап урока | Деятельность учителя | Деятельность учеников |
| 1 .Организационный момент | Рассказывает о том, чем будут заниматься на уроке | Ученики рассаживаются за парты, приготавливаются к уроку. Слушают учителя |
| 2. Историческая справка | Работает с презентацией, которую демонстрирует на проекторе и, с помощью которой рассказывает об интересных фактах из истории развития теории пределов, демонстрируя основные фразы и портреты ученых на слайдах. | Ученики сидят за партами, внимательно смотрят на проектор и внимательно слушают учителя, что он рассказывает и показывает на проекторе. Записывая основные моменты из рассказа учителя об истории теории пределов в тетрадь. Задают вопросы, если им осталось что не понятным |
13


 3. Об интуитивном понятии «Предел последовательности»
3. Об интуитивном понятии «Предел последовательности» Учитель продолжает
Учитель продолжаетработать с проектором,
демонстрирует в
презентации 2 примера:
Первый пример
сопровождает рисунками на
слайде; второй пример
сначала показывает в
реальности (бросает мячик),
потом на слайдах
показывает с помощью
рисунков, суть
эксперимента.
Каждый раз сначала показывает эксперимент, далее просит учащихся на интуитивном уровне сделать вывод, потом показывает на слайдах вывод (вне зависимости правильно ли сделали вывод учащиеся или нет)
 Учащиеся сидят за партами,
Учащиеся сидят за партами,внимательно следят за ходом
эксперимента, который
демонстрируется на проекторе. Делают выводы, которые просит учитель. Делают записи в тетрадь, которые просит делать учитель.

 4. Формулировка математического определения
4. Формулировка математического определенияПрежде чем сформулировать
определение «Предел
последовательности»
учитель проводит
небольшую практическую
работу учениками на
компьютерах, указывая
действия, которые должны выполнить ученики. Задает вопросы по результатам работы.
Далее формулирует строго
математическое
определении «Предела
последовательности».
Ученики рассаживаются за
персональные компьютеры и
индивидуально выполняют
лабораторную работу.(Если
компьютеров не хватит
персонально каждому ученику, то ученики работают в паре). Потом отвечают на вопросы, которые задает учитель по результату работы. Записывают определения в тетрадь с проектора.
 14
14



 5. Объяснение парадокса «Ахиллес и черепаха»
5. Объяснение парадокса «Ахиллес и черепаха»6
 . Итог урока
. Итог урокаПроводит практическую
работу на компьютерах по
осуществлению парадокса,
указывая действия, которые
должны выполнить ученики.
После этой работы,
объясняет решение
парадокса, демонстрируя решения на слайдах.
Учитель подводит итог проделанной работы на уроке.
Ученики продолжают работу за персональными компьютерами, проводят парадокс. Потом отвечают на вопросы, которые задает учитель по результату работы.
Рассаживаются за парты, следят за
решением парадокса, которое
продемонстрировано на слайдах
презентации учителя, записывают
решение парадокса в тетрадь.
Говорят о возникших трудностях, непонимания. Обсуждают их с учителем. Также проводят рефлексию своей работы на уроке.
З
 амечания для учителя
амечания для учителя1.Для построения на координатной прямой точек (рис.1,рис.2). Учителю (ученику) необходимо воспользоваться программой ГРАФЕР («Открытая математика 2.5. Функции и графики»).
на панели инструментов выберете закладку Главная. Нажмите двойным щелчком на кнопку Холст. В результате откроется окно Свойства. Холст, где вам необходимо задать границы шкалы и шаг сетки по осям, чтоб получилась координатная прямая. Нажмите ОК.
нажмите на кнопку Точка. Поставьте соответствующие точки на координатной прямой.
2. Для проведения парадокса «Ахиллес и черепаха» необходимо воспользоваться программой МОДЕЛЬ («Открытая математика 2.5. Функции и графики »). выберете модель 1.3 «Ахиллес и черепаха»
при помощи полей численного ввода можно изменить начальные параметры парадокса.
при помощи группы переключателей выберите интересующий вас режим: Показать парадокс или Снять парадокс.
нажмите Старт. В окне вывода вы сможете увидеть соответствующие выбранному режиму математические выкладки.
15
в «парадоксальном» режиме нажимайте каждый раз кнопку Дальше, чтобы перейти к следующему шагу.
Кнопка Стоп приостанавливает анимацию, кнопка Сброс возвращает ее в исходное состояние.
16
Обоснование выбора ЦОР
В работе с мультимедийным курсом ООО «Физикон» «Открытая математика 2.5 Математика» я отдаю предпочтение применению компьютерных моделей. Наилучший вариант оборудования -компьютерный класс с проектором. Он обеспечивает все формы работы с моделями в классе под руководством учителя. Однако, приведённый урок показывает пример, использования компьютерных моделей при наличии одного компьютера учителя, оснащённого мультимедийным проектором и экраном в обычном кабинете математики и персональных компьютеров для учеников. Материалы с наименьшей степенью интерактивности, например презентация сопровождающая конспект урока на большом экране, используются как иллюстрации к теоретическому материалу. Для интерактивных моделей применяется диалоговая форма работы. Она заключается в том, что ученики высказывают возможные способы решения задач, а учитель работает за компьютером, реализуя поступающие предложения. При этом необязательно отсеивать заблуждения учащихся. Иногда, умышленно выбирая неверные предложения, можно достичь большего эффекта, обучая на заблуждениях. Интерактивные модели позволяют проводить фронтальные лабораторные работы, когда действия за компьютером выполняет учитель, а весь класс следит за процессом решения и может направлять, уточнять и проверять свои предположения. Также модели развивают любознательность и интерес к математики.
17
Заключение
В действительности, компьютер выполняет лишь формальную (вернее формализованную) сторону обучения и дает возможность преподавателю переключиться на неформальную, творческую, психологическую сторону учебного процесса. Роль учитель не уменьшается, а возрастает, так как он теперь превращается из рентранслятора знаний в соучастника усвоения и понимания знаний обучающимся. Даже в будущем машина никогда не может полностью заменить учителя, который выполняет функцию не только обучения, но и воспитания, которое не поддается формализации и требует личного контакта. Но компьютер освобождает учителя от массы однообразной нетворческой работы и высвобождает время для творческой педагогической деятельности, увеличивая его эффективность.
Таким образом, отвергая мнение об обучающих информационных средствах, как универсальных средствах решения всех педагогических проблем, можно утверждать, что внедрение этих средств в процесс образования оказывает огромное воздействие на те качественные изменения, которыми подвержена современная система образования.
В заключении хотелось бы отметить, что использование ЦОР в процессе изучения темы «Предел последовательности», позволит решить ряд поставленных нами целей:
- Формирование у учащихся понятия «Предел последовательности»;
- Формирование представлений о Математике как универсальном языке науки; средстве моделирования явлений и процессов;
- Развивать элементы логического мышление, умение делать вывод;
- Развивать любознательность, познавательный интерес у учащихся;
- Воспитать средствами математики культуры личности через знакомство с историей развития понятия «Предел последовательности».
- Развитие у учащихся элементов способности видеть и использовать в учебной деятельности межпредметные связи, знания других наук.
18
Библиографический список
- Мордкович А.Г «Алгебра и начала анализа 10-11 класс», Мнемозина.-
2001
- Электронное приложение
- www.math.ru
- www. Edication.ru
19
