Метод 

Вид материала

Лекция

Содержание Рассмотрим следующее дерево Возможны 2 случая

Подобный материал:

• Темы курсовых работ по курсу «Программирование» для студентов группы биб-11-1 (2011-2012, 85.51kb.
• Практических: 0 Лабораторных:, 21.53kb.
• Урока литературы в 9 классе на тему: «Древнерусская литература и современность. Золотое, 43.48kb.
• Расшифровка : Наука в целом (информационные технологии 004), 79.71kb.
• Программа исследования, 416.21kb.
• Решение. Из анализа схемы следует, что резисторы, 80.22kb.
• 1. Предмет и метод. Основные понятия экономики, 49.49kb.
• Линейных алгебраических уравнений ax=B, где, 66.22kb.
• 1 Встатье рассматриваются вопросы соотношения, 1701.62kb.
• Теоретичні питання з курсу „ Аналітична геометрія та лінійна алгебра, 24.09kb.

Лекция №5


Метод отсечения


Идея метода была предложена Дж. Маккарти в 1961 г.

В основе метода лежит то, что процессы построения и отсечения ДИ происходят одновременно.

Существуют 2 случая  отсечения:

1. Неглубокое (простое)  отсечение.
   
2. Глубокое  отсечение.
   

1. Неглубокое  отсечение

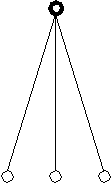
Рассмотрим следующее дерево:

S



A (MAX)




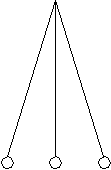
a b

f(a) =  …………

B (MIN)

Заведомо неперспективное направление при ходе игрока В


c

f(c) = z

Пусть нам известны оценки f(a)= и f(c)=z. Докажем, что если f(c), то остальные ветви, исходящие из вершины b можно отсечь.

Так как игрок B стремится минимизировать оценочную функцию, следовательно, оценка вершины b будет не больше z.

Так как оценка вершины b не больше z ( f(b)  f(c)   ), следовательно, вершина b неперспективна (т.к. f(a)=, а игрок A стремится максимизировать оценочную функцию).

Все вышесказанное справедливо для -отсечения.

Для -отсечения :

• ход делает игрок B
  
• f(a) = 
  
• f(c) = w
  

2. Глубокое  отсечение

Рассмотрим следующее дерево:

S




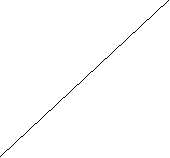
A


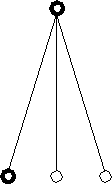a … b

f(a) = 


B

c …

f(c)  


A


d …


B

e …

f(e) = z  

Пусть нам известны оценки f(a)= и f(e)= z  . Докажем, что если f(e)  , то остальные ветви, исходящие из вершины d можно отсечь.

Так как игрок B стремится минимизировать оценочную функцию, следовательно, оценка вершины d будет не больше z (f(d)  f(e) = z  ).

Так как игрок A стремится максимизировать оценочную функцию, оценка вершины c будет не меньше оценки вершины d (f(с)  f(d)).

Возможны 2 случая:

1) f(c) = f(d), тогда f(c) = f(d)  f(e)   , т.е. имеем неглубокое  - отсечение;

2) f(c)  f(d), тогда вершина d неперспективна и для получения оценки f(c) не использовалась, а значит все вершины выходящие из d неперспективны.

Ход	Наилучшая оценка	Позиция на глубину	Оценка позиции	Условие отсечения	Действие
Свой A(MAX)		Своя	Z	z	-отсечение
Противник B(MIN)		Противника	W	w	-отсечение

 возрастает при построении оценки снизу вверх, а  убывает при построении оценки снизу вверх.


Пусть оценивается дерево на n уровней. На каждом уровне имеется m вариантов выбора. Тогда сложность вычислений:

• для метода максимина - mⁿ
  

• для метода  отсечений:
  

(при больших n  )


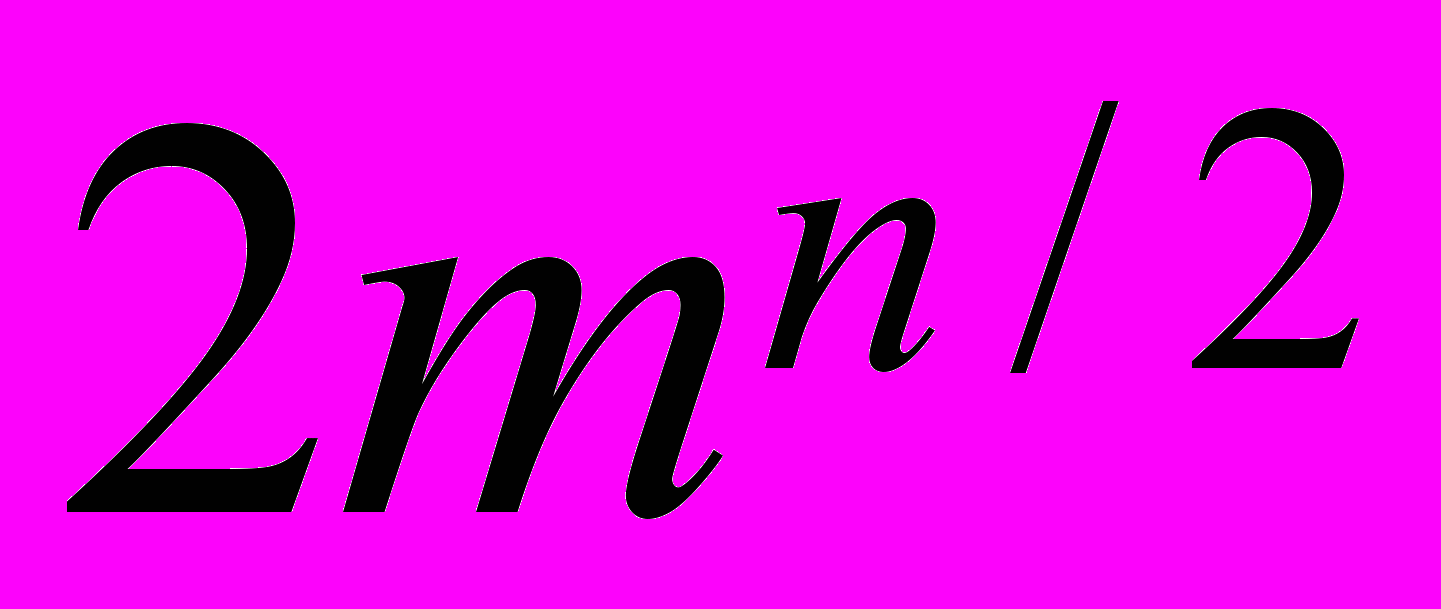Семинар №5


Задача №1:


Условие из примера в лекции №4.



5 S


3 1 4 1=zα=1 6 5 3 5 8 9 7 3=zα 4zα


n = 26

n_k = 13


A

4=3


α=5


B


β=4

4=3=zα


A


α=1


5

3

7=w=5

3

4


B

Недостатки методов МАКСИМИНА и  отсечений


1) Оба метода не являются стратегиями и базируются на классических переборных алгоритмах, с использованием оценочной функции.


2) Эффект горизонта.