Теоретичні питання з курсу „ Аналітична геометрія та лінійна алгебра

Вид материала

Документы

Содержание Пряма в просторі. Взаємне розташування прямої і площини в просторі. Лінійний (векторний) простір.

Подобный материал:

• Назва модуля: Математичний аналіз, 55.07kb.
• Назва модуля: Аналітична геометрія, 57.54kb.
• Опсік, іі-курс “Лінійна алгебра та аналітична геометрія”, 15.71kb.
• Назва модуля: Імітаційне моделювання Код модуля, 20.82kb.
• Лінійна алгебра та аналітична геометрія, 30.94kb.
• Кнлу 2009/2010 навч рік Екзаменаційні питання з курсу “Вища математика” Розділ І. Аналітична, 47.8kb.
• Алгебра І аналітична геометрія, 36.4kb.
• Підсумкові контрольні роботи з математики у 5-6 класах, 69.15kb.
• Формат опису модуля, 42.09kb.
• План Лінійна однорідна система диференціальних рівнянь з постійними коефіцієнтами Лінійна, 186.96kb.

ТЕОРЕТИЧНІ ПИТАННЯ

з курсу „Аналітична геометрія та лінійна алгебра»,

для студентів І курсу спеціальності «6.040203. Фізика» заочної форми навчання

(2010/2011 н.р.)


ЧАСТИНА 1

1. Визначники другого і третього порядку. Властивості визначників. Приклади.
   
2. Визначники вищих порядків. Розклад визначника за елементами рядка (стовпця).
   
3. Матриці. Дії над ними. Обернена матриця. Приклади.
   
4. Системи лінійних рівнянь. Основні означення. Методи розв’язування (метод Крамера, метод Гауса, матричний метод). Приклади.
   
5. Теорема Кронекера-Капеллі.
   
6. Вектори. Лінійні операції над ними. Властивості. Приклади.
   
7. Напрямні кути вектора. Проекція вектора на вектор. Поділ відрізка у відношенні .
   
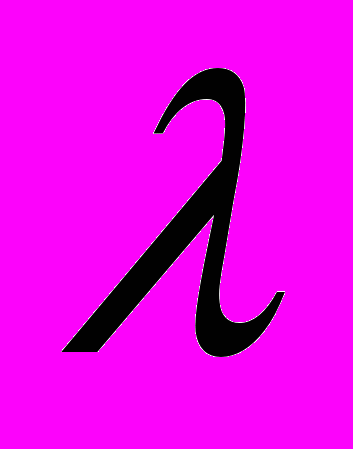8. Скалярний добуток векторів. Властивості. Застосування. Приклади. Кут між векторами.
   
9. Векторний добуток векторів. Властивості. Застосування. Приклади.
   
10. Мішаний добуток векторів. Властивості. Застосування. Приклади.
    
11. Різні види рівнянь прямої на площині: рівняння прямої, що проходить через задану точку паралельно до заданого вектора. Канонічне рівняння. Рівняння прямої, що проходить через дві задані точки. Рівняння прямої у відрізках на осях. Рівняння прямої з кутовим коефіцієнтом. Рівняння прямої, що проходить через задану точку в заданому напрямі. Приклади.
    
12. Взаємне розташування прямих на площині. Умови паралельності і перпендикулярності. Кут між прямими. Приклади.
    
13. Відстань від точки до прямої. Приклади
    
14. Криві другого порядку. Коло. Еліпс. Гіпербола. Парабола. Приклади.
    

ЧАСТИНА 2

1. Площина. Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора. Загальне рівняння площини. Дослідження неповного рівняння площини. Нормальне рівняння площини. Рівняння площини, що проходить через 3 точки. Рівняння площини у відрізках на осях. Кут між двома площинами. Відстань від точки до площини.
   
2. Пряма в просторі. Рівняння прямої, о проходить через задану точку паралельно до заданого вектора. Параметричні рівняння прямої. Пряма як перетин двох площин. Кут між двома прямими. Умова перетину двох прямих в просторі. відстань від точки до прямої. Відстань між двома прямими.
   
3. Взаємне розташування прямої і площини в просторі. Перетин прямої і площини. Кут між прямою і площиною. Основні задачі на пряму і площину в просторі. Умова належності двох прямих площині.
   
4. Поверхні другого порядку. Сфера. Циліндричні поверхні. Поверхні обертання: еліпсоїд, однопорожнинний та двопорожнинний гіперболоїди, параболоїди: еліптичний та гіперболічний. Конус.
   
5. Лінійний (векторний) простір. Означення векторного простору. Приклади. Властивості. Лінійно залежна та лінійно незалежна системи векторів. Базис та розмірність векторного простору. Матриця переходу від одного базису до іншого.
   
6. Лінійні оператори. Означення та основні властивості. Матриця ЛО. Операції над ЛО. Область значень та ядро ЛО. Власні вектори та власні значення ЛО. Спряжений лінійний оператор.
   
7. Квадратичні форми. Зведення квадратичної форми до головних осей.
   
8. Комплексні числа. Алгебраїчна, тригонометрична форми комплексного числа. Геометричне зображення. Операції над комплексними числами, формула Муавра, добування кореня з комплексного числа.
   
9. Група. Означення, приклади.
   

Лектор доц. О.О.Требенко