Наведённая проводимость

Вид материала

Документы

Содержание Наименьшего действия прин­цип Наименьшего принуждения принцип Флуктуации электричес­кие. Наложения принцип Намагниченность остаточная J=0), намагничивать в монотонно и медленно возрастающем поле, то полу­чающуюся зависимость J (H) Рис. 1. а — кривая первого намагничивания; 6 — схематич. изображение процессов намаг­ничивания в многодоменном ферромагнетике. J, связанным с необрати­мым смещением междоменных границ. Н. на этом участке происходит скачка­ми (см. Баркгаузена эффект). Намагничивания кривые Рис. 2. Семейство симметричных петель ги­стерезиса (г) и осн. кривая намагничивания (1) для молибденового пермаллоя; Н Намагничивающая сила Направленность акустичес­ких излучателей и приемни­ков Напряжения главные R — радиус витка с током I); в центре соленоида на его оси H=nI (n — Напряженность электриче­ского поля Нарушенное полное внутрен­нее отражение В. М. Золотарев. Насыщенный пар Небесная механика В. В. Белецкий. ... Полное содержание

Подобный материал:

• Электрический ток в газах самостоятельная и несамостоятельная проводимость газов, 128.37kb.
• Полимерные системы в катализе и электрокатализе возможности и перспективы, 16.03kb.
• Ионная проводимость сложных фосфатов со структурой nasicon а 3-2 X Nb X m 2- X (po, 389.98kb.
• 1. Проводимость (проводник, полупроводник, изолятор, ток, напряжение, сопротивление,, 98.07kb.
• Лекция2 проводимость полупроводников виды проводимости, 502.09kb.
• Кристаллические и стеклообразные фазы в системах biF 3 Bi 2 o 3 BaF, 505.44kb.
• Квч терапии у больных стенокардией, 43.39kb.
• 1. Энергетические зоны и свободные носители заряда в твердых телах. Уровень Ферми, 21.7kb.

Н

НАВЕДЁННАЯ ПРОВОДИМОСТЬ, то же, что возбуждённая проводимость.

НАВЬЕ — СТОКСА УРАВНЕНИЯ [по имени франц. учёного Л. Навье (L. Navier) и англ. учёного Дж. Стокса (G. Stokes)], дифференциальные ур-ния движения вязкой жидкости (газа). Для несжимаемой (плотность =const) и ненагреваемой (темп-ра Т=const) жидкости Н.— С. у. в проекциях на оси прямоугольной декар­товой системы координат (система трёх ур-ний) имеют вид:



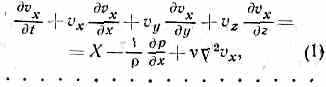
Здесь t — время, х, у, z — координа­ты жидкой ч-цы, v_x, v_y, v_z — проек­ции её скорости, X, Y, Z — проекции объёмной силы, р —-давление, v=/ — кинематич. коэфф. вязкости (— динамич. коэфф. вязкости),



Два других ур-ния получаются заме­ной х на у, у на z и z на х. Н.— С. у. служат для определения v_x.,v_y, v_z, p как функций x, у, z, t. Чтобы замкнуть систему, к ур-ниям (1) присоединяют ур-ние неразрывности, имеющее для несжимаемой жидкости вид:



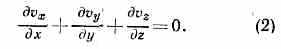
Для интегрирования ур-ний (1), (2) требуется задать начальные (если дви­жение не явл. стационарным) и гра­ничные условия, к-рыми для вязкой жидкости явл. условия прилипания к твёрдым стенкам. В общем случае (движение сжимаемой и нагреваемой жидкости) в Н.— С. у. учитывается ещё переменность  и зависимость  от темп-ры, что изменяет вид ур-ний. При этом дополнительно используют­ся ур-ние баланса энергии и Клапейро­на уравнение. Н.— С. у. применяют при изучении движения реальных жидкостей и газов, причём в большин­стве конкретных задач ограничивают­ся приближёнными решениями.

• См. лит. при ст. Гидроаэромеханика.

С. М. Тарг.

НАИМЕНЬШЕГО ДЕЙСТВИЯ ПРИН­ЦИП, один из вариационных принци­пов механики, согласно к-рому для данного класса сравниваемых друг с другом движений механич. системы действительным является то, для кото­рого физ. величина, наз. действием, имеет наименьшее (точнее, стационар­ное) значение. Обычно Н. д. п. приме­няется в одной из двух форм.

а) Н. д. п. в форме Гамильтона — Остроградского устанавливает, что среди всех кинематически возможных перемещений системы из одной кон-

фигурации в другую (близкую к пер­вой), совершаемых за один и тот же промежуток времени, действительным является то, для к-рого действие по Гамильтону S будет наименьшим. Матем. выражение Н. д. п. имеет в этом случае вид: S=0, где  — символ неполной (изохронной) вариации (т. е. в отличие от полной вариации в ней время не варьируется).

б) Н. д. п. в форме Мопертюи — Лагранжа устанавливает, что среди всех кинематически возможных пере­мещений системы из одной конфигура­ции в близкую к ней другую, совершае­мых при сохранении одной и той же ве­личины полной энергии системы, дей­ствительным является то, для к-рого действие по Лагранжу W будет наи­меньшим. Матем. выражение Н. д. п. в этом случае имеет вид W=0, где  — символ полной вариации (в отли­чие от принципа Гамильтона — Остро­градского, здесь варьируются не толь­ко координаты и скорости, но и время перемещения системы из одной конфи­гурации в другую). Н. д. п. в. этом случае справедлив только для консер­вативных и притом голономных систем, в то время как в первом случае Н. д. п. является более общим и, в частности, может быть распространён на некон­сервативные системы. Н. д. п. поль­зуются для составления ур-ний движе­ния механич. систем и для исследова­ния общих св-в этих движений. При соответствующем обобщении понятий Н. д. п. находит приложения в меха­нике непрерывной среды, в электро­динамике, квант. механике и др.

• См. лит. при ст. Вариационные принципы механики.

С. М. Тарг.

НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ ПРИНЦИП, то же, что Гаусса прин­цип.

НАИМЕНЬШЕЙ КРИВИЗНЫ ПРИН­ЦИП, то же, что Герца принцип.

НАЙКВИСТА ФОРМУЛА (теорема Найквиста), соотношение, определяю­щее величину тепловых флуктуаций тока или напряжения в электрич. цепи. Получено амер. физиком X. Найквистом (Н. Nyquist) в 1928. Со­гласно Н. ф., обусловленное тепловы­ми флуктуациями ср. значение квад­рата напряжений на концах провод­ника с сопротивлением R, находяще­гося в состоянии теплового равнове­сия при абс. темп-ре Т, равно:

V² = 4RkTv, (1)

где v — полоса частот, внутри к-рой измеряются флуктуации напряжения. При низких темп-pax и достаточно высоких частотах v, когда hvkT, вме­сто формулы (1) пользуются более общим выражением:



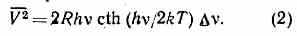
• Киттель Ч., Элементарная статисти­ческая физика, пер. с англ., М., 1960. См. также лит. при ст. Флуктуации электричес­кие.

Э. М. Эпштейн.

НАКАЧКА в квантовой электронике, процесс создания неравновесного со­стояния вещества под воздействием электромагнитных полей, при соуда­рениях с заряж. или нейтр. частица­ми, при резком охлаждении предва­рительно нагретых газовых масс и т. п. Н. может перевести в-во из состояния термодинамич. равновесия в активное состояние (с инверсией населённостей), в к-ром оно может усили­вать и генерировать эл.-магн. волны (см. Квантовая электроника, Лазер, Квантовый усилитель). Термин «Н.» применяется также в радиотехнике и оптике для обозначения процессов воздействия на элементы параметрич. систем.

НАКОПИТЕЛЬ заряженных частиц (накопительное кольцо), элемент сис­темы встречных пучков, представляю­щий собой кольцевую вакуумную ка­меру, находящуюся в магн. поле, в к-рой накапливаются и длительно циркулируют ч-цы от большого числа циклов ускорения заряж. ч-ц. См. Встречных пучков системы.

НАЛОЖЕНИЯ ПРИНЦИП, то же, что суперпозиции принцип.

НАМАГНИЧЕННОСТЬ, характери­стика магн. состояния макроскопич. тела; в случае однородно намагниченного тела Н. J определяется как маг­нитный момент М ед. объёма тела: J=M/V. В случае неоднородно на­магниченного тела Н. определяется для каждой точки тела (точнее, для каждого физически малого объёма dV): J=dM/dV, где dM — магн. мо­мент объёма dV. Ед. Н. в Междуна­родной системе единиц — ампер на метр (1 А/м — Н., при к-рой 1 м³ в-ва обладает магн. моментом 1 А•м³), в СГС системе единиц — эрг/(Гс•см³). Н. тел зависит от внеш. магн. поля и темп-ры (см. Парамагнетизм, Ферро­магнетизм). У ферромагнетиков за­висимость J от напряжённости внеш. поля Н выражается кривой намагни­чивания (см. Намагничивания кривые, Гистерезис). Н. тела зависит от на­пряжённости внеш. поля Н, магн. св-в в-ва этого тела, его формы и располо­жения во внеш. поле. Между напря­жённостью поля в в-ве h_b и полем H существует соотношение: Н_В=Н-NJ, где N — размагничивающий фактор. В изотропных в-вах направление J совпадает с направлением Н, в ани­зотропных направления J и Н в об­щем случае различны.

• Вонсовский С. В., Магнетизм, М., 1971; II а р се л л Э., Электричество и маг­нетизм, пер. с англ., М., 1971 (Берклеевский курс физики, т. 2).

443


НАМАГНИЧЕННОСТЬ ОСТАТОЧНАЯ, намагниченность J_r,к-рую име­ет ферромагн. материал при напря­жённости магн. поля H, равной нулю. Н. о. зависит как от магн. св-в мате­риала, так и от его магн. предысто­рии. (Н. о.— один из осн. параметров магн. гистерезиса.) Н. о. обусловлена задержкой изменения J при умень­шении Н (после предыдущего намаг­ничивания образца) из-за влияния магнитной анизотропии и структур­ных неоднородностей образца. При переходе от состояния макс. намаг­ниченности (в пределе — магн. насы­щения J_s) к состоянию Н. о. векторы J_s в отд. кристаллах поликрист. об­разца поворачиваются от направления Н к направлению осей лёгкого намагни­чивания, ближайших к Н. Т. о., J_r=_iJ_sv_icos_i, где сумма бе­рётся по всем j кристаллитам с объёма­ми vi и углами _i между Н и их осью лёгкого намагничивания; J — сум­марная намагниченность зародышей доменов с обратным направлением на­магниченности, возникших при умень­шении H до нуля и представляющих собой исходную ступень новой домен­ной структуры. В простейшем случае циклич. перемагничивания по симмет­ричному циклу Н. о. возрастает при возрастании макс. напряжённости по­ля от цикла к циклу, стремясь к ко­нечному пределу, наз. Н. о. данного материала. Н. о. материала (в-ва) не следует смешивать с Н. о. тела, т. е. со ср. намагниченностью тела в состоя­нии, когда H=0. Н. о. в-ва опреде­ляется при равенстве нулю магн. поля внутри тела (оно складывается векторно из полей всех внеш. источников и размагничивающего поля самого на­магниченного тела). Наиболее устой­чивой Н. о. обладают высококоэрци­тивные материалы (см. Коэрцитивная сила). При нагревании ферромагнети­ков до темп-ры, превышающей Кюри точку, они теряют ферромагнитные св-ва, а вместе с тем и Н. о. К уменьшению Н. о. приводят также ме­ханические сотрясения и вибрации. Явление Н. о. имеет широкое практи­ческое применение (см. Магнит по­стоянный).

• См. лит. при ст. Магнетизм.

НАМАГНИЧИВАНИЕ, процессы установления намагниченности, про­текающие в в-ве при действии на него внеш. магн. полем. В диамагнетиках Н. состоит в возникновении микро­скопических индукц. токов, создаю­щих намагниченность, направленную против внеш. магн. поля. В парамаг­нетиках происходит ориентация хао­тически колеблющихся магнитных мо­ментов атомов или ионов в направ­лении поля. При этом энергия от сис­темы магн. моментов передаётся крист. решётке в-ва и процесс Н. характери­зуется временем спин-решёточной ре­лаксации.

Более сложные процессы происхо­дят при намагничивании ферромагне­тика. В состоянии полного размагни­чивания ферромагн. образец состоит из большого числа доменов, каждый из к-рых намагничен до насыщения, но при этом их векторы намагниченно­сти J_s направлены так, что суммарный магнитный момент образца М=_iJ_si=0. Н. состоит в переориентации век­торов намагниченности доменов в на­правлении приложенного поля; вклю­чает процессы смещения, вращения и парапроцесс.

Процесс смещения в многодо­менном ферромагнетике заключается в перемещении границ между домена­ми; объём доменов, векторы J_S к-рых составляют наименьший угол с на­правлением напряжённости магн. поля Н, при этом увеличивается за счёт соседних доменов с энергетически ме­нее выгодной ориентацией J_s относи­тельно поля. При своём смещении границы доменов могут менять форму, размеры и собств. энергию. Эти фак­торы в одних случаях способствуют, в других препятствуют процессу сме­щения. Обычно задержка смещения (и Н.) происходит при встрече границы домена с к.-л. неоднородностями структуры ферромагнетика (атомами примесей, дислокациями, микротре­щинами и др.). Для возобновления смещения необходимо вновь изменять Н (либо темп-ру или давление).

Процесс вращения состоит в повороте векторов J_s в направлении поля Н. Причиной возможной задерж­ки или ускорения процесса вращения явл. магнитная анизотропия ферро­магнетика (первоначально векторы до­менов направлены вдоль осей лёгкого намагничивания, в общем случае не совпадающих с направлением Н). При полном совпадении J_s с направлением Н достигается т. н. техническое маг­нитное насыщение, равное величине J_s ферромагнетика при данной темп-ре.

Парапроцесс в большинстве случаев даёт очень малый прирост намагни­ченности, поэтому Н. ферромагнети­ков определяется в осн. процессами смещения и вращения.

Если ферромагнетик, находящийся в состоянии полного размагничивания ( J=0), намагничивать в монотонно и медленно возрастающем поле, то полу­чающуюся зависимость J (H) наз. кри­вой первого (первоначального) Н. (см. Намагничивания кривые). Эту кривую обычно подразделяют на пять участков (рис. 1, а и б). Участок I — область начального, или обратимого, намаг­ничивания, где J=_aH. В этой обла­сти протекают гл. обр. процессы упру­гого смещения границ доменов (при пост. начальной магнитной восприим­чивости _а). Участок II (область Рэлея) характеризуется квадратичной зависимостью J от Н (в этой области . линейно возрастает с H). В области Рэлея Н. осуществляется благодаря процессам смещения, как обратимым, линейно зависящим от H, так и необратимым, квадратично зависящим от H (см. Рэлея закон на­магничивания).



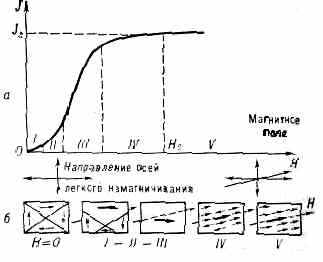
Рис. 1. а — кривая первого намагничивания; 6 — схематич. изображение процессов намаг­ничивания в многодоменном ферромагнетике.


Область наиб. проницаемостей (III) характеризуется быст­рым ростом J, связанным с необрати­мым смещением междоменных границ. Н. на этом участке происходит скачка­ми (см. Баркгаузена эффект). В обла­сти приближения к насыщению (IV) осн. роль играют процессы вращения. Участок V — область парапроцесса.



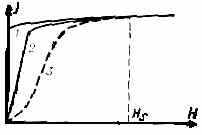
Рис. 2. Безгистерезисная кривая намагничивания: теоретическая (1) и эксперимен­тальная (2). Для сравнения приведена кривая первого на­магничивания (3). Наклон кривой (2) обусло­влен неоднородностями материала (пусто­тами, трещинами и т. п.), на к-рых образу­ются внутренние размагничивающие поля.


Если после достижения состояния магн. насыщения J_s (в поле H_s) начать уменьшать H, то будет уменьшаться и J, но по кривой, лежащей выше кри­вой первого намагничивания (магн. гистерезис). Гистерезис сказывается и при Н.— он затрудняет рост J с уве­личением поля, при отсутствии гисте­резиса значение J уже в слабых полях приближается к J_s, отличаясь от J_s



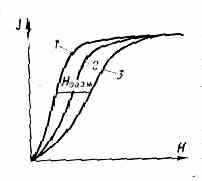
Рис. 3. Кривые на­магничивания фер­ромагн. образцов разл. длины и фор­мы: 1 — тороид; 2 — длинный тон­кий образец; 3 — короткий толстый образец; Н_разм— внутр. размагничи­вающее поле, зави­сящее от формы об­разца.


на величину, обусловленную процес­сами вращения. Вклад процессов сме­щения и вращения в результирую­щую намагниченность ферромагн. образца на различных участках кри­вой намагничивания зависит от его текстуры магнитной, наличия дефек­тов крист. решётки, формы образца и др. факторов. Существенное влияние

444


формы образца на ход кривой Н. обус­ловлено действием собств. магн. поля образца (размагничивающего фактора, рис. 3).

• Вонсовский С. В., Магнетизм, М.,

НАМАГНИЧИВАНИЯ КРИВЫЕ, графики, таблицы или формулы, пока­зывающие зависимость намагниченно­сти J или магнитной индукции В от напряжённости магнитного поля Н. Если известна зависимость J(H), то по ней можно построить для того же вещества кривую индук­ции В(Н), так как одновременно значения В, J, Н, относящиеся к од­ному элементу объёма вещества, свя­заны соотношением: B=H+4J (в СГС системе единиц) или В=₀ (H+J) (в ед. СИ, здесь ₀ — магнитная по­стоянная).

Н. к. магнитных материалов зави­сят не только от физ. св-в материалов и внеш. условий, но и от последова­тельности прохождения различных



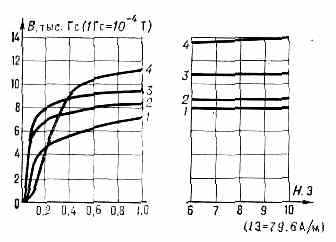
Рис. 1. Кривые первого намагничивания пермаллоевых сплавов: 1 — хромовый пермал­лой (78% Ni, 3,8% Cr, остальное Fe); 2 — молибденовый пермаллой (79% Ni, 4% Mo, 0,2% Mn, остальное Fe); 3 — пермаллой с 75,8% Ni, 24,2% Fe; 4 — пермаллой с 45% Ni, 55% Fe.

магн. состояний, в связи с чем рассмат­ривают неск. видов Н. к.: а) кривые первого намагничивания (рис. 1) — последовательности значений J (H) или В(Н) в-ва при монотонном возраста­нии Н из нач. состояния с B=H=J=0 (при этом Н не меняет направления); б) кривые цикличного перемагничивания (статич. петли гистерезиса) —



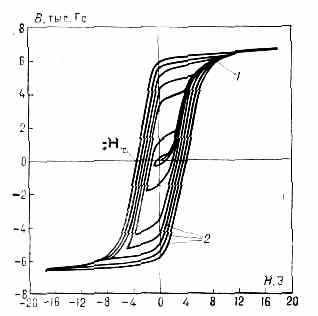
Рис. 2. Семейство симметричных петель ги­стерезиса (г) и осн. кривая намагничивания (1) для молибденового пермаллоя; Н_c — ко­эрцитивная сила.


зависимости В (Н) или J(Н), получае­мые после многократного прохожде­ния определ. интервала значений Н в прямом и обратном направлениях (рис. 2); в) основные (или коммутаци­онные) кривые — геом. место вершин симметричных петель перемагничивания (рис. 2) и др.

По Н. к. определяют хар-ки магн. материалов (намагниченность оста­точную, коэрцитивную силу, магнит­ную проницаемость и др.), они служат для расчётов магнитных цепей элек­тромагнитов, магн. пускателей, реле и др. электротехнич. устройств и приборов.

• Бозорт Р. М., Ферромагнетизм, пер. с англ., М., 1956.

НАМАГНИЧИВАЮЩАЯ СИЛА, то же, что магнитодвижущая сила.

НАНО... (от греч. nanos — карлик), приставка к наименованию единицы физической величины для образования названия дольной единицы, равной 10^-9 от исходной единицы. Обозначе­ния: н, n. Пример: 1 нм (нанометр)=10^-9 м.

НАПОР в гидравлике, линейная величина, выражающая удельную (отне­сённую к ед. веса) механич. энергию потока жидкости в данной точке. Пол­ный запас уд. энергии потока Н (пол­ный Н.) определяется Бернулли урав­нением: H=z+p_v/+v²/2g , где z — высо­та рассматриваемой точки над пло­скостью отсчёта, p_v — давление жид­кости, текущей со скоростью v,  — уд. вес жидкости, g — ускорение силы тяжести. Два первых слагаемых трёх­члена определяют собой сумму удель­ных потенц. энергий положения (z) и давления (p_vl), т. е. полный запас удельной потенц. энергии, наз.

г и д р о с т а т и ч е с к и м Н., а третье слагаемое — удельную кинетич. энер­гию (скоростной Н.). Вдоль потока Н. уменьшается. Разность Н. в двух поперечных сечениях потока реальной жидкости H₁-H₂=h_v наз. потерянным Н. При движении вязкой жидкости по трубам потерян­ный Н. вычисляется по Дарси — Вейсбаха формуле.

НАПРАВЛЕННОСТЬ АКУСТИЧЕС­КИХ ИЗЛУЧАТЕЛЕЙ И ПРИЕМНИ­КОВ, способность излучать (прини­мать) звук. волны в одних направлени­ях в большей степени, чем в других. При излучении направленность акустич. преобразователя обусловливается интерференцией когерентных звук. ко­лебаний, приходящих в каждую точку среды от отд. малых по сравнению с длиной волны в среде участков излу­чателя, а при приёме — интерферен­цией давлений на поверхности приём­ника.

Н. а. и. и п. обычно описывают: характеристикой направ­ленности — отношением звук. дав­ления в данном направлении к его значению в направлении макс. излу­чения на том же расстоянии от излу­чателя, представленном в ф-ции направления, и к о э ф ф и ц и е н т о м к о н ц е н т р а ц и и, или коэфф. направленного действия, т. е. отношением ин­тенсивности звука, создавае­мой данным излучателем в на­правлении макс. излучения, к интенсивности ненаправленного излучателя той же мощности на том же расстоянии.



Хар-ку направленности в сечении нек-­рой плоскостью, проходящей через на­правление макс. излучения, представ­ляют обычно в полярной системе коор­динат (рис.).

НАПРЯЖЕНИЕ механическое, мера внутр. сил, возникающих при дефор­мации материала. Для введения поня­тия «Н.» мысленно вырезается из сре­ды нек-рый объём, по поверхности F к-рого распределены силы вз-ствия с остальной частью среды, возникаю­щие при деформации. Если Р — равнодействующая (гл. вектор) сил вз-ствия на элементе поверхности F, содержащем рассматриваемую точку А, то предел отношения P/F при F0 наз. вектором на­пряжения S_n в точке А на пло­щадке с нормалью п. Величины про­екций вектора Н. на нормаль n и на касательную плоскость наз. нормаль­ным _n и касательным _n напряжения­ми. Н. наз. у с л о в н ы м, если при его вычислении сила относится к пло­щади сечения в недеформированном состоянии, и и с т и н н ы м, если учтено изменение площади при дефор­мации. Чтобы определить напряжён­ное состояние в точке, надо найти ве­личины, по к-рым можно вычислить Н. на любой из бесчисл. множества пло­щадок, проходящих через эту точку. Вектор Н.