Наведённая проводимость

Вид материала

Документы

Содержание Нелинейная акустика Нелинейная оптика Историческая справка. Взаимодействие сильного светового поля со средой. Рис. 1. Сравнение эксперим. значений ку­бичной восприимчивости  Оптические гармоники. Рис. 2. Сечения по­верхностей показате­лей преломления в кристалле КН

Подобный материал:

• Электрический ток в газах самостоятельная и несамостоятельная проводимость газов, 128.37kb.
• Полимерные системы в катализе и электрокатализе возможности и перспективы, 16.03kb.
• Ионная проводимость сложных фосфатов со структурой nasicon а 3-2 X Nb X m 2- X (po, 389.98kb.
• 1. Проводимость (проводник, полупроводник, изолятор, ток, напряжение, сопротивление,, 98.07kb.
• Лекция2 проводимость полупроводников виды проводимости, 502.09kb.
• Кристаллические и стеклообразные фазы в системах biF 3 Bi 2 o 3 BaF, 505.44kb.
• Квч терапии у больных стенокардией, 43.39kb.
• 1. Энергетические зоны и свободные носители заряда в твердых телах. Уровень Ферми, 21.7kb.

р) (ξ — энергия квазичастицы, р — её квазиимпульс), время жизни и характер вз-ствия с др. квазичастицами. Магноны исследуются с помощью неупру­гого когерентного магн. рассеяния.

Некогерентное рассеяние нейтронов. Упругое некогерентное ядерное рас­сеяние даёт информацию только о вероятности процесса рассеяния без передачи энергии. Квазиупругое рас­сеяние (с очень малыми передаваемы­ми энергиями ~10^-3—10^-7 эВ) даёт сведения о самодиффузии атомов и мо­лекул в жидкостях, диффузии прото­нов в металлах, колебаниях макромо­лекул в растворах и др. Упругое неко­герентное магн. рассеяние позволяет исследовать пространств. распределе­ние магнитно-активных эл-нов в отд. парамагн. атомах.

Неупругое некогерентное яд. рас­сеяние в моно- и поликристаллах по­зволяет исследовать фононный спектр и динамику отд. некогерентно рассеи­вающих центров, напр. протонов в ме­таллах, небольших молекул и мол. групп (NH₃CH₃ и др.) в сложных водородсодержащих кристаллах и т. п. Неупругое некогерентное магн. рас­сеяние применяется при исследовании структуры электронных уровней осн. мультиплетов парамагн. ионов в ме­таллах и металлидах. Некогерентный неупругий процесс даёт информацию сразу о всех возможных возбуждени­ях, т. е. о плотности состояний квази­частиц.

Экспериментальные методы. Источ­ником нейтронов в Н. обычно явл. ядерный реактор. Измерение энергии нейтрона производят: а) с помощью нейтронных дифракц. монохроматоров М (монокристаллы Cu, Zn и др., рис. 2, а, в) или многослойных отра­жающих зеркал; б) с помощью фильт­ров А (рис. 2, г) из в-в, обладающих «окном» прозрачности для нейтронов в определённой области энергий (напр., Be прозрачен для энергий 5•10^-3 эВ);

в) по времени пролёта (рис. 2, б);

г) методами монохроматизации поляризов. нейтронов (резонансный метод и метод спинового эха). Резонансный метод основан на явлении резонансного переворачивания спина нейтрона в стационарном магн. поле с прост­ранств. периодичностью вдоль ней­тронного пучка. При нек-ром выборе

457


периода и величины магн. поля ней­троны определённой энергии испыты­вают переворачивание спина и могут быть отделены от нейтронов др. энер­гий. Метод нейтронного спинового эха основан на ларморовской прецессии спина нейтрона во внеш. магн. поле.



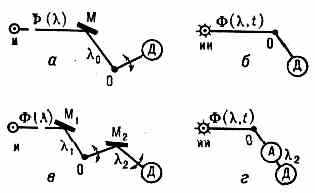
Рис. 2. Схемы нейтронографич. экспериментов: И — источник нейтронов, ИИ — им­пульсный источник, M — кристалл — монохроматор, О — исследуемый образец, Д — детектор, А — фильтр—анализатор; а и 6 — изучение упругого, в и г — неупругого рассеяний нейтронов.


Этот способ позволяет обнаружить из­менение энергии нейтрона порядка 10^-7—10^-10 эВ. Для анализа неупру­гого рассеяния нейтронов использует­ся метод времени пролёта с фильтром перед детектором (рис. 2, г).

• Г у р е в и ч И. И., Тарасов Л. В., Физика нейтронов низких энергий, М., 1965; И з ю м о в Ю. А., Озеров Р. П., Маг­нитная нейтронография, М., 1966; Кри­воглаз М. А., Теория рассеяния рент­геновских лучей и тепловых нейтронов реальными кристаллами, М., 1967; Рассея­ние тепловых нейтронов, под ред. П. Игелстаффа, пер. с англ., М., 1970; Нейтроны и твердое тело, под ред. Р. П. Озерова, т. 1—2, М., 1879—81; Александров Ю. А., Шарапов Э. И., Чер Л., Дифракционные методы в нейтронной физи­ке, М., 1981; Динамические свойства твер­дых тел и жидкостей. Исследование методом рассеяния нейтронов, пер. с англ., под ред. С. Лавси, Т. Шпрингера, М., 1980.

А. М. Балагуров, Ю. М. Останевич.

НЕЛИНЕЙНАЯ АКУСТИКА, об­ласть акустики, изучающая явления, для описания к-рых обычные прибли­жения линейной теории звука недоста­точны и необходим учёт нелинейных членов ур-ний гидродинамики и ур-ния состояния. Обычно такие явления, т. я. нелинейные эффекты, возникают при распространении звук. волн большой интенсивности (т. н. волн конечной амплитуды) и проявляются во вз-ствии разл. мод гидродинамич. возмущения, отсутствующих в рамках линейного приближения, характеризующегося выполнением суперпозиции принципа. Нелинейные эффекты в акустич. поле можно рассматривать как результат изменения св-в среды, вызванного рас­пространяющейся волной и влияюще­го как на распространение данной вол­ны (самовоздействие), так и на рас­пространение др. гидродинамич. воз­мущений (вз-ствие). К нелинейным эффектам относятся: изменение формы волны в процессе её распространения, т. е. изменение временной зависимо­сти параметров волны, возникновение комбинационных тонов при рассеянии

звука на звуке, самофокусировка вол­ны, давление звук. излучения, акус­тич. течения, кавитация и др.

Характерной чертой нелинейных эф­фектов явл. их зависимость от ампли­туды волны, в отличие от явлений линейной акустики (напр., дифракции волн, рассеяния звука), определяемых лишь частотой и скоростью звук. вол­ны. Их относит. вклад характеризует­ся безразмерной величиной — Маха числом M=v/c='/, где v — амплиту­да колебательной, скорости частиц, с — скорость звука, ' — обусловлен­ная волной избыточная плотность,  — равновесное значение плотности. Учёт нелинейных членов в ур-ниях гидро­динамики и ур-ниях состояния приво­дит не только к нелинейным поправкам порядка М, малым при М<<1, во и к накапливающимся при распростране­нии волны эффектам, к-рые радикаль­но изменяют картину распростране­ния волны даже при малых М. Пример такого накапливающегося эффекта — искажение формы волны при её рас­пространении, обусловленное разни­цей в скоростях перемещения разл. точек профиля волны. Точки, соответ­ствующие областям сжатия, «бегут» быстрее точек, соответствующих об­ластям разрежения. Происходит это от того, что скорость звука в области сжатия больше, чем в области разре­жения, а также из-за увлечения вол­ной среды, к-рая в области сжатия движется в направлении распростра­нения волны, а в области разреже­ния — в противоположном. Для волн малой интенсивности, когда M<<1, эта разница скоростей пренебрежимо мала и волна успевает затухнуть, прежде



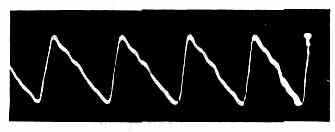
Экспериментально зарегистрированный про­филь первоначально синусоидальной вол­ны на расстоянии 100 длин волн от излу­чателя. Амплитуда давления пилообразной волны 10 атм, частота 0,775 МГц.


чем в ней разовьются нелинейные эф­фекты. Распространение таких волн происходит практически без измене­ния их формы, в соответствии с реше­ниями ур-ний линейной акустики, ос­нованных на предположении о посто­янстве скорости звука для всех точек профиля волны. Если же интенсив­ность волны достаточно велика, то влияние накапливающихся нелиней­ных эффектов сильнее, чем влияние диссипативных процессов, обусловли­вающих затухание волны, поэтому первоначально синусоидальная волна переходит в пилообразную (рис.). Рас­стояние, на к-ром происходит этот пе­реход, зависит от амплитуды и длины волны. Со спектр. точки зрения, иска­жение формы волны означает нарастание высших гармонич. составляющих осн. частоты и явл. частным случаем нелинейного взаимодействия акустиче­ских волн.

Примером ненакапливающихся не­линейных эффектов может служить давление звукового излучения, обуслов­ленное передачей импульса от волны к препятствию. Другой пример — акус­тические течения. Своеобразным нели­нейным эффектом в акустич. поле, воз­никающем при распространении звука в жидкости, явл. кавитация, к-рая также сопровождается перераспреде­лением энергии по спектру акустич. волны.

• Зарембо Л. К., Красильников В. А., Введение в нелинейную аку­стику, М., 1966; Мощные ультразвуковые поля, под ред. Л. Д. Розенберга, М., 1968.

К. А. Наугольных.

НЕЛИНЕЙНАЯ ОПТИКА, раздел оп­тики, охватывающий исследования распространения мощных световых пучков в тв. телах, жидкостях и газах и их вз-ствия с в-вом. Сильное свето­вое поле изменяет оптич. хар-ки среды (показатель преломления, коэфф. по­глощения), к-рые становятся ф-циями напряжённости электрич. поля Е све­товой волны, т. е. поляризация среды нелинейно зависит от Е. Н. о. имеет много общего с нелинейной теорией колебаний (см. Нелинейные системы), нелинейной акустикой и др.

Историческая справка. Начало совр. этапа в развитии Н. о. (1961) связано с созданием лазеров, к-рое открыло возможности изучения и использова­ния нелинейных явлений фактически во всех областях физ. и прикладной оптики. С появлением лазеров оптика получила источники когерентного из­лучения большой мощности. С по­мощью импульсных лазеров можно получить интенсивности света I~10⁷—10⁹ Вт/см². Мощные лазерные системы позволяют получить I~10¹⁶ Вт/см². Напряжённости светового поля Е (I пропорц. Е²) в таких пучках сравнимы или даже превышают внутриатомные поля. В таких световых нолях возни­кают новые оптич. эффекты и сущест­венно изменяется характер уже извест­ных явлений.

Вместе с тем ясные представления о том, что законы линейной оптики (су­перпозиции принцип) носят прибли­жённый характер и применимы лишь для не слишком сильных световых полей, существовали и до появления лазеров. Ок. 50 лет назад С. И. Вави­ловым были поставлены эксперименты с целью обнаружения нелинейных яв­лений. В 1923 Вавилов и В. Л. Лёвшин обнаружили уменьшение погло­щения света урановым стеклом с рос­том интенсивности света и объяснили это тем, что в сильном эл.-магн. поле большая часть атомов (или молекул) находится в возбуждённом состоянии и уже не может поглощать свет. Счи­тая, что это лишь один из множества возможных оптич. нелинейных эффек­тов, Вавилов впервые ввёл термин «Н. о.». В 50-х гг. Г. С. Горелик тео-

458


ретически рассмотрел возможность на­блюдения ряда нелинейных оптич. эффектов с помощью фотоэлектрич. умножителей. Один из них — смеще­ние оптич. дублета с выделением раз­ностной частоты, лежащей в диапазоне СВЧ (г е т е р о д и н и р о в а н и е с в ет а),— наблюдали в 1955 А. Форрестер, Р. Гудмундсен и П. Джонсон (США). К Н. о. в широком смысле относятся и хорошо известные электро-оптические эффекты (линейный Поккельса эффект и квадратичный Керра эффект). Оказалось, что влияние низ­кочастотного электрич. поля на пока­затель преломления среды имеет ту же физ. природу, что и такие нелинейно-оптич. явления, как генерация оптич. гармоник и смешение частот (си. ниже).

В 1961 П. Фрайкен с сотрудниками (США) открыл эффект удвоения часто­ты света в кристаллах — генерацию 2-й гармоники. В 1962 наблюдалось утрое­ние частоты (генерация 3-й гармони­ки). В 1961—63 в СССР (Р. В. Хохлов, С. А. Ахманов) и в США (Н. Бломберген) были получены фундаментальные результаты в теории нелинейных оптич. явлений, заложившие теор. основы Н. о. В 1962—63 открыто и объяснено вынужденное комбинационное рассея­ние света, что послужило толчком к изучению вынужденного рассеяния др. видов. В 1965 обнаружена самофокуси­ровка света. При этом мощный световой пучок, распространяясь в среде, во многих случаях не испытывает обыч­ной, т. н. дифракционной, расходимо­сти, а, напротив, самопроизвольно сжимается.

В 1965 были созданы параметриче­ские генераторы света, в к-рых не­линейные оптич. эффекты используют­ся для генерирования когерентного оптич. излучения, плавно перестраи­ваемого по частоте в широком диапа­зоне длин волн . В 1967 началось ис­следование нелинейных явлений, свя­занных с распространением в среде сверхкоротких (длительностью до 10^-12 с) световых импульсов. С 1969 развиваются методы нелинейной и ак­тивной спектроскопии (см. ниже).

Наиболее важные разделы совр. Н. о.: волновая Н. о., исследования нелинейной поляризации среды и не­линейная спектроскопия, прикладная Н.о.

Взаимодействие сильного светового поля со средой. Элем. процесс, лежа­щий в основе вз-ствия света со сре­дой,— возбуждение атома или моле­кулы световым полем и переизлучение света возбуждённой ч-цей. Матем. опи­санием этих процессов явл. ур-ния, связывающие поляризацию Р ед. объ­ёма среды с напряжённостью поля E (м а т е р и а л ь н ы е у р а в н е н и я). Линейная оптика базируется на приближённом соотношении:

р=е, (1)

где  — диэлектрическая восприимчи­вость, зависящая только от св-в среды

(см. Диэлектрики). Согласно (1), пере­излучённое поле имеет ту же частоту, что и падающее, следовательно, ур-ние (1) не описывает ни возникновения оптич. гармоник, ни др. нелинейные эффекты. Это означает, что соотноше­нием (1) можно пользоваться лишь в области слабых световых полей.

Суть приближений, лежащих в ос­нове (1), можно понять, обращаясь к классич. модели осциллятора, исполь­зуемой для описания вз-ствия света с в-вом. Поведение атома или молекулы в световом поле эквивалентно колеба­ниям осциллятора. Характер отклика ат. осциллятора на световую волну можно установить, сравнивая E с на­пряжённостью внутриатомного поля E_ae/a²10⁸ —10⁹ В/см (е — заряд эл-на, a — ат. радиус), определяющего силы связи в ат. осцилляторе. В пуч­ках нелазерных источников Е1—10 В/см, т. е. Е<<Е_а, и ат. осциллятор можно считать гармоническим. Пря­мым следствием этого явл. (1). В пуч­ках мощных лазеров можно получить Е вплоть до 10⁶ —10⁷ В/см, уже срав­нимые с Е_а. При этом осциллятор ста­новится ангармоническим, нелиней­ным, что приводит к нелинейной зави­симости между поляризацией среды Р и E. При (E/E_a)<1 P можно предста­вить в виде разложения в ряд но параметру Е/Е_а:

P=⁽¹⁾E+⁽²⁾E²+⁽³⁾E³+... (2)

Коэфф.⁽¹⁾, ⁽²⁾ и т. д. наз. н е л и н е й н ы м и в о с п р и и м ч и в о с т я м и (по порядку величины ⁽¹⁾~ ~1/E_a; ⁽²⁾~1/E²_a. Ур-ние (2) явля­ется основой Н. о. Если на поверх­ность среды падает монохроматич. световая волна Е=Аcos(t-kx), где А — амплитуда,  — частота, k — вол­новое число, х — координата точки вдоль направления распространения волны, t — время, то, согласно (2), поляризация среды наряду с линейным членом Р^Л =⁽¹⁾Acos(t-kx) содер­жит ещё и нелинейный член 2-го по­рядка:



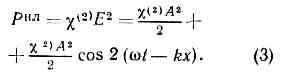
Последнее слагаемое в (3) описывает поляризацию, изменяющуюся с часто­той 2, т. е. генерацию 2-й гармоники. Генерация 3-й гармоники, а также за­висимость показателя преломления n от интенсивности описываются членом ⁽³⁾E³ в (2) и т. д. [член с ⁽²⁾ описы­вает также линейный злектрооптич. эффект, если в (2) представить Е в ви­де: Е=Е₀+Е_св, где Е₀ — статич. по­ле, Е_св — электрич. поле световой волны, а член с  ⁽³⁾ описывает эффект Керра].

Нелинейный отклик ат. или мол. ос­циллятора на сильное световое поле — наиболее универсальная причина не­линейных оптич. эффектов. Существу­ют и др. причины: напр., изменение показателя преломления n может быть вызвано нагревом среды лазерным из­лучением. Изменение темп-ры T=Е² ( — коэфф. поглощения света) приводит к изменению n от n₀ до n=n₀+(дn/дT)T. Во мн. случаях сущест­венным оказывается также эффект электрострикции (сжатие среды в све­товом поле Е). В сильном световом по­ле Е лазера электрострикц. давление, пропорц. Е², изменяет плотность сре­ды, что может привести к генерации звук. волн. С тепловыми эффектами связана самодефокусировка света.

Нелинейные восприимчивости ⁽²⁾, ⁽³⁾, ⁽⁴⁾ и т. д.— новые параметры вещества (рис. 1). Изучение их дисперсии (зависимости от со) — пред­мет нелинейной спектроскопии. Для атомов методами квантовой механики



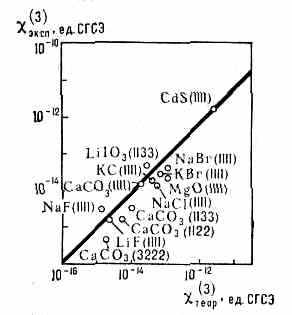
Рис. 1. Сравнение эксперим. значений ку­бичной восприимчивости ⁽³⁾ для разл. кри­сталлов с теоретическими; т. к. ⁽³⁾ — тензор 4-го ранга, то сравниваются конкретные компоненты тензора.


удаётся рассчитать нелинейные вос­приимчивости любого порядка. Их дисперсия имеет сложный вид, так как резонансы возникают не только при совпадении частот действующих полей с собственными частотами ато­ма, но и при совпадении с ними тех или иных комбинаций этих частот. В не слишком сильных лазерных полях совпадение результатов теории и эксперимента оказывается хорошим. Для простых молекул вблизи их колебательно-вращат. резонансов дис­персия нелинейной восприимчивости имеет много общего с дисперсией не­линейной восприимчивости атомов вблизи их электронных резонансов. Гораздо сложнее картина для элек­тронных переходов в больших моле­кулах и конденсированных средах. Несмотря на то, что квантовомеханический расчёт в этих случаях невоз­можен, была развита феноменологи­ческая теория, позволившая полу­чить количественные результаты, во мн. случаях хорошо согласующиеся с экспериментом (рис. 1), и дать ре­цепты поиска новых нелинейно-оптич. материалов. В то время как значения

459


⁽²⁾ для подавляющего большинства оптич. материалов отличаются между собой не более чем на один порядок, значения ⁽³⁾ отличаются на три по­рядка. Это свидетельствует об особой физ. информативности нелинейных св-в в-ва.

Оптические гармоники. На рис. 1 на вклейке к стр. 528 показано, как интенсивное монохроматич. излуче­ние лазера на неодимовом стекле (=1,06 мкм), проходя через оптически прозрачный кристалл ниобата бария, преобразуется в излучение с =0,53 мкм, т. е. во 2-ю гармонику. При нек-рых условиях во 2-ю гармо­нику переходит более 60% энергии падающего излучения. Более сложные эффекты возникают, если в среде рас­пространяются две или неск. интен­сивных волн с разл. частотами, ₁ и ₂. Тогда наряду с гармониками каж­дой из волн (2₁, 2₂ и т. д.) возника­ют волны с комбинац. частотами (₁+ ₂, ₁-₂ и т. п.).

Генерация оптич. гармоник имеет много общего с умножением частоты в нелинейных элементах радиоуст­ройств, однако в оптике эти эффекты явл. результатом вз-ствия со средой не колебаний, а волн. Т. к. свет рас­пространяется в среде, размеры L к-рой существенно превышают , сум­марный эффект генерации гармоник на выходе зависит от фазовых соотноше­ний между осн. волной и гармониками внутри среды; возникает своеобразная интерференция, способная либо уси­лить, либо ослабить эффект. Можно ожидать, что вз-ствие двух волн, напр.  и 2, максимально, а следователь­но, максимальна и перекачка энергии от осн. волны  к гармонике 2, если их фазовые скорости равны (условие



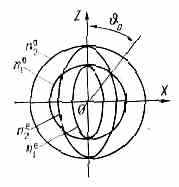
Рис. 2. Сечения по­верхностей показате­лей преломления в кристалле КН₂РО₄ для частоты излу­чения неодимового лазера (индекс 1) и его 2-й гармоники (индекс 2). В пло­скости OXZ сечения для обыкновенных волн (n⁰) — окружности, для необыкновенных волн (n^е) — эллипсы. Под углом ₀ к оп­тической оси OZ n⁰₁=n^e₂, а следовательно, равны и фазовые скорости осн. обыкновен­ной и 2-й гармоники необыкновенной волн.

фазового синхронизма). С квант. то­чки зрения, это условие соответствует закону сохранения импульса k при слиянии или распаде фотонов. Для трёх волн условия синхронизма имеют вид: k₃=k₁+k₂, где k₁ k₂ и k₃ — им­пульсы фотонов (в ед. n).

Равенство фазовых скоростей волн на разных частотах имеет место лишь в среде без дисперсии (см. Дисперсия волн). Однако выяснилось, что отсутствие дисперсии можно имитировать, используя вз-ствие волн разной поля­ризации в анизотропной среде, в част­ности в кристаллах (рис. 2). В нек-рых кристаллах есть направления, вдоль к-рых фазовая скорость одинакова для основной обыкновенной волны и необыкновенной волны 2-й гармоники (см. Кристаллооптика и рис. 2). Этот метод резко повысил эффективность нелинейных волновых взаимодействий. Если в 1961 кпд оптических удвоите­лей частоты составлял 10^-10—10^-12, то современные удвоители имеют кпд -0,8.

Оптич. умножители частоты исполь­зуются для преобразования излучения ДВ лазеров в излучение KB диапазо­нов. Обычно для этой цели служат процессы генерации 2-й и 3-й гармо­ник, но в нек-рых случаях интерес представляют и нелинейные явления более высокого порядка. Благодаря нелинейной поляризации n-го порядка P⁽ⁿ⁾=⁽ⁿ⁾еⁿ световая волна частоты  возбуждает n-ю гармонику _n=n, и при достаточно больших n использование умножения частоты по­зволяет сразу продвинуться доста­точно далеко в KB область спектра.



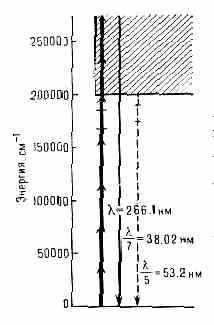
Рис. 3. Энергетич. схема генерации 5-й и 7-й оптич. гармоник в атомах Не; горизон­тальными штрихами отмечены положения энергетич. уровней атома Не, заштри­хована область сплошного спект­ра.


Однако нелинейные восприимчиво­сти ⁽ⁿ⁾ быстро уменьшаются с ростом n(⁽ⁿ⁾~1/E^(n-1)_a), и поэтому для по­лучения заметного нелинейного эф­фекта необходимы достаточно мощные световые пучки. Предел здесь опреде­ляется не мощностью лазеров, а конку­рирующими нелинейными явлениями в в-ве и прежде всего его оптич. пробоем. Поэтому возможности исполь­зования высших нелинейностей в той или иной среде обусловливаются в пер­вую очередь её лучевой прочностью. Т. к. эта величина возрастает по мере сокращения длительности лазерного импульса, то используются сверхко­роткие импульсы длительностью 10^-11—10^-12 с.

В благородных газах или парах ме­таллов предельные плотности мощно­сти для пикосекундных лазерных им­пульсов значительно выше, чем в конденсиров. средах (10¹²—10¹³ Вт/см²). В этих условиях становится эффек­тивной генерация 5-й и даже 7-й гар­моник, обусловленная нелинейностями ⁽⁵⁾ и ⁽⁷⁾ [в газе отличны от нуля только нечетные члены в (2)]. Указан­ные процессы были использованы для получения когерентного излучения в области далёкого вакуумного ультра­фиолета. Мощные сверхкороткие ла­зерные импульсы с =2661 нм воз­буждали газообразный Не; на выходе кюветы с Не было зарегистрировано излучение 5-й (=53,2 нм) и 7-й (=38,02 нм) гармоник (рис. 3). Это пока кратчайшая длина волны когерентно­го излучения.