Наведённая проводимость

Вид материала

Документы

Содержание Напряжения главные R — радиус витка с током I); в центре соленоида на его оси H=nI (n — Напряженность электриче­ского поля Нарушенное полное внутрен­нее отражение В. М. Золотарев. Насыщенный пар Небесная механика В. В. Белецкий. Неголономные системы Неймана принцип Нейтральный ток Слабое взаимодействие). С. М. Биленький.

Подобный материал:

• Электрический ток в газах самостоятельная и несамостоятельная проводимость газов, 128.37kb.
• Полимерные системы в катализе и электрокатализе возможности и перспективы, 16.03kb.
• Ионная проводимость сложных фосфатов со структурой nasicon а 3-2 X Nb X m 2- X (po, 389.98kb.
• 1. Проводимость (проводник, полупроводник, изолятор, ток, напряжение, сопротивление,, 98.07kb.
• Лекция2 проводимость полупроводников виды проводимости, 502.09kb.
• Кристаллические и стеклообразные фазы в системах biF 3 Bi 2 o 3 BaF, 505.44kb.
• Квч терапии у больных стенокардией, 43.39kb.
• 1. Энергетические зоны и свободные носители заряда в твердых телах. Уровень Ферми, 21.7kb.

S₁, действующий на элем. площадке, перпендикулярной оси Ох₁, в проекциях на оси координат Ох₁х₂х₃ обозначают через ₁₁, ₁₂, ₁₃, а для элем. площадок, перпендикулярных осям Ох₂ и Ох₃,— через ₂₁, ₂₂, ₂₃ и ₃₁, ₃₂, ₃₃. При этом ₁₁, ₂₂, ₃₃ — нормальные Н., а ₁₂=₂₁, ₂₃=₃₂, ₃₁=₁₃ — касательные Н. Шесть ве­личин _ij (i, j=1, 2, 3) образуют тен­зор напряжений в рассмат­риваемой точке. Н. на любой площад­ке в той же точке вычисляется через величины _ij, т. е. тензор Н. полно­стью определяет напряжённое состоя­ние в точке. Если известны _ij как ф-ции координат, то они определяют напряжённое состояние всего тела. На­пряжённое состояние наз. однород­ным, если _ij не зависят от координат

точки. Величина =1/3(₁₁+₂₂+₃₃)

наз. средним (гидростатическим) Н. В каждой точке тела есть три взаимно перпендикулярные площадки, на к-рых касательные Н. равны нулю. Перпендикуляры к ним наз. глав­ными осями Н. в точке, а нор­мальные Н. на них ₁, ₂, ₃ — глав-

445


ными Н. См. также Девиатор на­пряжений, Интенсивность напряже­ний.

Непосредственно Н. не измеряется. В однородном напряжённом состоянии Н. вычисляется через величины дейст­вующих на тело сил. В неоднородном напряжённом состоянии Н. опреде­ляется косвенно — по эффектам его действия, напр. по пьезоэлектрич. эффекту, эффекту двойного лучепре­ломления (см. Поляриаационно-оптический метод исследования).

• Ильюшин А. А., Л е н с к и й В. С., Сопротивление материалов, М., 1959.

В. С. Ленский.

НАПРЯЖЕНИЕ электрическое, см. Электрическое напряжение.

НАПРЯЖЕНИЯ ГЛАВНЫЕ, см. Напряжение механическое.

НАПРЯЖЁННОСТЬ МАГНИТНОГО ПОЛЯ, векторная величина Н, яв­ляющаяся количеств. хар-кой магн. поля. Н. м. п. не зависит от магн. св-в среды. В вакууме Н. м. п. совпадает с магнитной индукцией В, численно H=B в СГС системе единиц и H=В/₀ в , Международной системе единиц (СИ), ₀ — магнитная постоянная. В среде Н. м. п. Н определяет тот вклад в магн. индукцию B, к-рый дают внеш. источники поля: Н=В-4J (в систе­ме ед. СГС) или H=(B/₀)-J (в СИ), где J— намагниченность среды. Если ввести магнитную проницаемость сре­ды , то для изотропной среды Н=В/₀ (в СИ). Единица Н. м. п. в СИ — ампер на метр (А/м), в системе ед. СГС — эрстед (Э); 1 А/м=4Х10^-3 Э1,256•10^-2 Э.

Н. м. п. прямолинейного провод­ника с током I (в СИ) H=Il2a (a — расстояние от проводника); в центре кругового тока H=I/2R ( R — радиус витка с током I); в центре соленоида на его оси H=nI (n — число витков на ед. длины соленоида). Практич. опре­деление Н в ферромагн. средах (в магн. материалах) основано на том, что тангенциальная составляющая Н не изменяется при переходе из одной среды в другую. Методы измерения Н. м. п. рассмотрены в ст. Магнитные измерения, Магнитометр.

НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕ­СКОГО ПОЛЯ, векторная величина E, являющаяся осн. количеств. хар-кой электрич. поля; определяется отношением силы, действующей со сто­роны поля на электрич. заряд, к вели­чине заряда (при этом заряд должен быть малым, чтобы не изменять ни величины, ни распределения тех за­рядов, к-рые порождают исследуемое поле). В вакууме Н. э. п. удовлетво­ряет принципу суперпозиции, соглас­но к-рому полная напряжённость поля в точке равна геом. сумме напряжённостей полей, создаваемых отд. заряж, ч-цами. Для электростатич. поля Н. э. п. может быть представлена как гра­диент электрич. потенциала : Е=-grad. В системе СИ Н. э. п, измеряется в В/м.

НАРУШЕННОЕ ПОЛНОЕ ВНУТРЕН­НЕЕ ОТРАЖЕНИЕ (НПВО), явле­ние, основанное на проникновении световой волны из оптически более плотной среды (с показателем прелом­ления n₁) в менее плотную среду (с по­казателем преломления n₂) на глубину порядка длины волны при полном внутреннем отражении. Нарушение полного внутр. отражения заключает­ся в том, что коэфф. отражения света R от границы раздела сред становится меньше единицы вследствие поглоще­ния света в слое, в к-рый проникает волна в отражающую среду. Степень ослабления отражённой волны зави­сит от поляризации падающей волны и пропорц. показателю поглощения ₂ второй среды, а спектр НПВО по­добен спектру поглощения этой среды. Нарушение полного внутр. отражения, несущественное для геом. оптики, по­служило основой для развития т. н. спектроскопии НПВО, имеющей ряд преимуществ перед традиц. методами исследования спект­ров отражения и поглощения. Осо­бенно эффективен метод НПВО для ис­следований поверх­ностных оптич. св-в объектов, а также для сильно поглощающих сред. Схема измерения оптич. постоянных приве­дена на рисунке (I₀ — интенсивность падающей, а I — отражённой свето­вой волны). Для выполнения условия полного внутр. отражения (n₂<1) исследуемое в-во приводится в идеаль­ный контакт с оптич. элементом (обыч­но призмой), прозрачным в выбранном диапазоне частот, с большим n₁ (кри­сталлы — корунд, фианит, германий и др., оптич. керамика, халькогенидные стёкла и т. п.). Нужный контакт легко достигается при исследовании жидкостей. Тв. тела приводятся в оп­тический контакт с вспомогат. оп­тич. элементом или в кач-ве среды с большим n₁ используется специально выбранная жидкость. В рентг. диапа­зоне эл.-магн. волн вспомогательный оптич. элемент не требуется, посколь­ку все в-ва в этой области имеют n₂<1 и условие n₂1 выполняется на гра­нице с воздухом. На практике спектры НПВО получают при углах падения i, значительно больших критич. угла j_кр=arcsin(n₂/n₁), а показатель по­глощения вычисляется из соотноше­ния: R=ехр(-₂d'), где d' — путь, пройденный лучом света в исследуе­мой среде.

Для увеличения контрастности спек­тров НПВО увеличивают число отра­жений (метод многократного НПВО — МНПВО), что эквивалентно увеличе­нию d'. Методы НПВО особенно эфф. для интервала 1 •10^-2<₂<1, тогда как при использовании метода погло­щения в этом случае необходимы объ­екты микронной толщины. Малые ₂



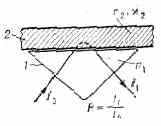
измеряются при ii_кр, и используется возникающая при этом поверхностная оптич. волна, распространяющаяся вдоль поверхности исследуемого тела на сравнительно большое расстояние. Из спектров НПВО и МНПВО можно определить оптич. постоянные n₂ и ₂ в-ва с помощью Френеля формул и Крамерса — Кронига соотношения.

Разл. модификации методов НПВО применяются для аналитич. целей и в физ. эксперименте: изучаются поверх­ностные эл.-магн. волны (плазмоны, поляритоны), адсорбционные явления, структура тонких слоев и т. д. Явле­ние НПВО следует учитывать при пере­даче световых сигналов на большое расстояние с помощью световодов.

• X а р р и к Н., Спектроскопия внутрен­него отражения, пер. с англ., М., 1970; З о л о т а р е в В. М.,

К и с л о в с к и й Л. Д., О возможностях изучения контуров полос в спектрофотометрии НПВО, «Оптика и спектроскопия», 1965, т. 19, в. 5, с. 809; З о л о т а р е в В. М., Л ы г и н В. И.,

Т а р а с е в и ч Б. Н., Спектры внут­реннего отражения поверхностных соедине­ний и адсорбированных молекул, «Успехи химии», 1981, т. 50, в.1, с. 24.

В. М. Золотарев.

НАСЕЛЕННОСТЬ УРОВНЯ (заселён­ность уровня), число ч-ц в ед. объема в-ва, находящихся в определённом энергетич. состоянии (на данном энергетич. уровне). См. Уровни энергии. НАСЫЩЕННЫЙ ПАР, пар, находя­щийся в термодинамич. равновесии с жидкостью (или тв. телом) того же хим. состава. Жидкость и её Н. п. находятся в состоянии дпнамич. рав­новесия: число молекул, переходя­щих из жидкости в пар в ед. времени, равно числу молекул пара, возвращающихся в жидкость за то же время. Н. п., содержащий капельки жидко­сти, наз. влажным, а не содержащий — сухим. Состояние сухого Н. п. неус­тойчиво: при малейшем отводе теплоты он частично конденсируется и стано­вится влажным, а при подводе теплоты превращается в перегретый пар. В ин­тервале темп-р и давлений, в к-ром возможно термодинамич. равновесие жидкости и пара (между тройной точ­кой и критической точкой), каждому давлению соответствует определ. темп-pa насыщения пара.

НЕБЕСНАЯ МЕХАНИКА, наука о движении небесных тел. Она изучает поступат., вращат., деформационные движения естеств. и искусств. небес­ных тел под влиянием сил гравитац. вз-ствия, воздействия среды, эл.-магн. сил, сил светового давления и др. Проблемы Н. м.: 1) теория движения больших планет Солн. системы. Клас­сическая Н. м. изучает движение боль­ших планет, рассматривая их как ма­териальные точки, тяготеющие друг к другу и к Солнцу по закону всемир­ного тяготения. Методы теории возму­щений позволили описать движение планет достаточно точно. Выдающим­ся достижением классич. теории стало теор. открытие в 1845 Нептуна англ. астрономом Дж. Адамсом и франц. астрономом У. Леверье. В совр. эпоху практика косм. полётов существенно

446


повысила требования к точности тео­рии движения планет. Это привело к появлению ряда фундам. работ (гл. обр. в СССР, США, Японии) по уточ­нению движения больших планет. 2) Теория движения малых планет (ас­тероидов), в к-рой можно выделить два перспективных направления: построе­ние уточнённых теорий движения отд. астероидов в связи с задачами освое­ния косм. пр-ва; построение глобаль­ных теорий, объясняющих существую­щее распределение элементов орбит астероидов. 3) Создание теории дви­жения комет, в частности в связи с перспективами косм. полётов к ним. 4) Задача о движении естеств. спутни­ков планет. 5) Проблема трёх тел — важная модельная задача о движении трёх взаимно тяготеющих материаль­ных точек, напр. косм. аппарата в сис­теме Земля — Луна или астероида в системе Солнце — Юпитер. Особый ин­терес представляет изучение равновес­ного движения к.-л. тела в полях тяготения двух других тел — опреде­ление св-в т. н. «точек либрации», ввиду их перспективности для прак­тики косм. полётов (см. Трёх тел за­дача). 6) Теория движения Луны — одна из сложных и до сих пор акту­альных задач Н. м. 7) Проблема ус­тойчивости Солн. системы. Постановка проблемы и первые результаты при­надлежат франц. учёным П. Лапласу и Ж. Лагранжу. Достижения матема­тики последних лет (теория Колмого­рова — Арнольда — Мозера) позво­лили существенно продвинуть решение классич. проблемы об устойчивости Солн. системы. В. И. Арнольдом по­лучен след. результат: большие полу­оси орбит планет, их наклонения и экс­центриситеты вечно остаются вблизи исходных значений, если эксцентри­ситеты орбит и их наклонения малы (это условие выполняется), а периоды обращения несоизмеримы (условие нерезонансности движений в системе). В реальной Солн. системе дело обстоит, скорее, наоборот: резонансные соот­ношения между частотами, характери­зующими орбит. движения тел Солн. системы, явл. правилом. 8) Резонанс­ные проблемы небесной механики. Средние движения планет довольно точно удовлетворяют нек-рым резо­нансным соотношениям между часто­тами их обращения вокруг Солнца (наиб. известен резонанс 5 : 2 для Юпитера и Сатурна). Известны и резо­нансные соотношения между ср. дви­жениями естеств. спутников планет. Осевое вращение Луны (и мн. других естеств. спутников планет) находится в соизмеримости 1 : 1 с орбит. дви­жением; осевое вращение Меркурия имеет с орбит. движением соизмери­мость 3:2. Обилие подобных фактов (здесь перечислена лишь малая их часть) позволяет предположить, что тенденция к резонансным движениям в H. м. есть объективная закономер­ность, к-рую можно использовать, напр., для стабилизации движения

ИСЗ. Построение теории, объясняю­щей эти факты во всей их полноте,— актуальная задача Н. м. 9) Теория вращат. движений естеств. небесных тел. Она развивалась классической Н. м. применительно к вращению Зем­ли и Луны (лунно-солн. прецессия и нутация земной оси, законы Кассини вращения Луны, классич. линейная теория либрации Луны). В 20 в. эти теории продолжают успешно разви­ваться, расширяется область их при­ложения. Так, установлена двойная синхронизация (двойной резонанс) ме­жду осевым вращением и орбит. дви­жением небесного тела, между движе­нием осп вращения тела и возмущён­ной прецессией орбиты — т. н. обоб­щённые законы Кассини, к-рым под­чиняется вращение Меркурия и ряда естеств. спутников планет. 10) Теория движения (поступательного и враща­тельного) искусств. небесных тел — большой раздел Н. м., появившийся в сер. 20 в. в связи с задачами, постав­ленными практикой косм. полётов. Эти задачи аналогичны задачам о движе­нии естеств. небесных тел, но требуют, как правило, учёта большого числа факторов. Усложнение задач косм. полётов выдвигает повышенные тре­бования не только к точности теории движения тел в космосе, но и к службе наблюдений.

Построение точных теорий движения искусств. косм. объектов способствует решению и нек-рых классич. задач Н. м., напр. определению фигур Зем­ли, Луны и др. планет Солн. системы.

• Дубошин Г. Н., Небесная механика. Основные задачи и методы, 3 изд., М., 1975; его же, Небесная механика. Аналитиче­ские и качественные методы, 2 изд., М., 1978; Грсбеников Е. Д., Рябов Ю. А., Новые качественные методы в небесной меха­нике, М., 1971; Маркеев А. II., Точки либрации в небесной механике и космодинамике, М., 1978; Белецкий В. В., Очер­ки о движении космических тел, 2 изд., М., 1977; его же, Движение искусственного спутника относительно центра масс, М., 1965; Справочное руководство по небесной механике и астродинамике, 2 изд., М., 1976; Эльясберг П. Е., Введение в теорию полета искусственных спутников Земли, М., 1965.

В. В. Белецкий.

НЕВЕСОМОСТЬ, состояние матери­ального тела, движущегося в поле тя­готения, при к-ром действующие на не­го силы тяжести или совершаемое им движение не вызывают давлений ч-ц тела друг на друга. Если тело покоится в поле тяжести Земли на горизонтальной плоскости, то на него действуют сила тяжести и направленная в проти­воположную сторону реакция плоско­сти, в результате чего возникают дав­ления ч-ц тела друг на друга. Челове­ческий организм воспринимает такие давления, как ощущение «весомости». Аналогичный результат имеет место для тела, к-рое находится в лифте, движущемся по вертикали вниз с ус­корением ag, где g — ускорение свободного падения. Но при a=g тело (все его ч-цы) и лифт совершают сво­бодное падение и никаких взаимных давлений друг на друга не, оказывают, т. е. имеет место Н.. При этом на все

ч-цы тела, находящегося в состоянии Н., действуют силы тяжести, но нет внеш. сил, приложенных к поверхно­сти тела (напр., реакций опоры), к-рые могли бы вызвать взаимные дав­ления ч-ц друг на друга. Подобное же состояние наблюдается для тел, помещённых в ИСЗ (или косм. кораб­ле); эти тела и все образующие их ч-цы, получив вместе со спутником соответствующую нач. скорость, дви­жутся под действием сил тяготения вдоль своих орбит с равными ускоре­ниями, как свободные, и не оказывают давлений друг на друга, т. е. находят­ся в состоянии Н.

Вообще тело под действием внеш. сил будет в состоянии Н., если: а) дей­ствующие внеш. силы явл. только мас­совыми (силы тяготения); б) поле этих массовых сил локально однородно, т. е. силы поля сообщают всем ч-цам тела в каждом его положении одина­ковые по величине и направлению ус­корения; в) нач. скорости всех ч-ц тела по величине и направлению оди­наковы (тело движется поступательно). Т. о., любое тело, размеры к-рого очень малы по сравнению с земным ра­диусом, совершая свободное поступат. движение в ноле тяготения Земли, будет, при отсутствии других внеш. сил, находиться в состоянии Н. То же имеет место при движении в поле тя­готения любых др. небесных тел.

Вследствие значит. отличия условий Н. от земных условий, в к-рых созда­ются и отлаживаются приборы и агре­гаты ИСЗ, косм. кораблей и их ракет-носителей, проблема Н. занимает важ­ное место среди др. проблем космо­навтики.

Особенно необходимо учитывать своеобразие условий Н. при полёте обитаемых косм. кораблей: условия жизни человека в состоянии Н. резко отличаются от привычных земных, что вызывает изменения ряда его жиз­ненных функций. Поэтому при длит. полётах человека на орбитальных (око­лоземных) или межпланетных станци­ях предполагается создавать искусств. «тяжесть», к-рую можно получить, напр., располагая рабочие помещения в кабинах, вращающихся вокруг центр. части станции (т. е. движущих­ся непоступательно). Вследствие этого вращения тела в кабине будут прижи­маться к её боковой поверхности, к-рая будет играть роль «пола», а реакция «пола», приложенная к поверхностям тел, будет создавать искусств. «тя­жесть».

С. М. Тарг.

НЕГОЛОНОМНЫЕ СИСТЕМЫ, механич. системы, на к-рые, кроме геомет­рических, налагаются ещё кинематич. связи, не сводящиеся к геометрическим и наз. неголономными (см. Голономные системы). Пример Н. с.— шар, катя­щийся без проскальзывания по шеро­ховатой плоскости. При этом налагает­ся ограничение не только на положение

447


центра шара (геом. связь), но и на скорость точки его касания с плос­костью, к-рая в любой момент време­ни должна быть равна нулю (кинематич. связь, не сводящаяся к геометри­ческой) .

Движение Н. с. изучают с помощью спец. ур-ний (ур-ния Чаплыгина, Аппеля) или ур-ний, получаемых из дифф. вариационных принципов меха­ники.

• Добронравов В. В., Основы ме­ханики неголономных систем, М., 1970. См. также лит. при ст. Механика.

С. М. Тарг.

НЕЕЛЯ ТОЧКА (антиферромагнитная точка Кюри), темп-pa Т_Н, выше к-рой антиферромагнетик превращает­ся в парамагнетик (фазовый переход II рода). Вблизи Т_н наблюдается специфич. температурная зависимость физ. св-в антиферромагнетиков (тепло­ёмкости, коэфф. теплового расшире­ния, электропроводности и др.). Н. т. названа по имени франц. физика Л. Нееля (L. Neel). См. Антиферромагне­тизм.

НЕЙМАНА ПРИНЦИП, постулат, устанавливающий связь симметрии макроскопич. физ. св-в кристалла с сим­метрией его внеш. формы. Согласно Н. п., группа симметрии любого спон­танно присущего кристаллу физ. св-ва должна включать в себя опера­ции симметрии точечной группы сим­метрии кристалла (см. Симметрия кристаллов, Кристаллофизика, Кюри принцип). Установлен нем. физиком Ф. Э. Нейманом (F. Е. Neumann).

НЕЙТРАЛЬНЫЙ ТОК в квантовой теории поля, ток в слабом вз-ствии («слабый ток»), к-рый описывает пере­ходы без изменения электрич. зарядов ч-ц; аналог эл.-магн. тока. На опыте наблюдались лишь Н. т. без изменения странности, «очарования», лептонных зарядов и др. квант. чисел. Н. т. от­крыты в 1973 при изучении процессов вз-ствия нейтрино высоких энергий (1 ГэВ) с нуклонами. Наряду с обычными процессами образования мю­онов ^± при вз-ствии мюонных нейтрино и антинейтрино с нуклонами:

v_+N^-+адроны (1)

v^~_+N⁺+адроны (2)

сопровождающимися изменением за­ряда лептона,— заряженными токами (нейтральные v_, v^~_, переходят в за­ряженные ^-, ⁺), наблюдались безмюонные нейтринные процессы — Н. т.:

v_+N+адроны (3)

v^~_+N^~+адроны (4)


Отношения R_v и R_v^~ сечений процес­сов (3) и (1). (4) и (2) оказались рав­ными: R_v0,30; R_v^~0,35.

Н. т. естественно возникают в еди­ной теории слабого и эл.-магн. вз-ствий (см. Слабое взаимодействие). В соот­ветствии с этой теорией процессы (3) и

(4) обусловлены обменом нейтральным промежуточным векторным бозоном Z между нейтральными нейтринным и адронным слабыми токами (рис. 1) аналогично тому, как процесс рассея­ния эл-нов на нуклонах e^-+N е^-+адроны обусловлен обменом фото­ном между эл.-магн. электронным и адронным токами.

Обмен Z-бозоном между нейтрин­ным и электронным слабыми Н. т.



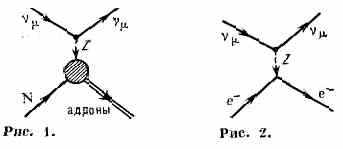
обусловливает процессы рассеяния v_ и v^~_ на эл-нах (рис. 2). Такие процес­сы также наблюдались эксперимен­тально; их сечения приблизительно в 10⁴ раз меньше сечений процессов (3) и (4).

Обмен Z-бозоном между электрон­ным Н. т. и адронным током обуслов­ливает слабое вз-ствие эл-на с нукло­ном. Такое вз-ствие приводит к нару­шению сохранения чётности в ат. переходах, в глубоко неупругом рас­сеянии продольно поляризов. эл-нов на неполяризов. нуклонах и др. Ожи­даемые эффекты чрезвычайно малы вследствие того, что между эл-нами и нуклонами имеется намного более ин­тенсивное, чем слабое, эл.-магн. вз-ствие, сохраняющее чётность. В 1978 такие эффекты несохранения чётности были наблюдены.

Все имеющиеся данные по Н. т. согласуются с теорией Глэшоу — Вайнберга — Салама.

• Биленький С. М., Лекции по физике нейтринных и лептон-нуклонных про­цессов, М., 1981; О к у н ь Л. Б., Лептоны и кварки, М., 1981.

С. М. Биленький.