Наведённая проводимость
| Вид материала | Документы |
- Электрический ток в газах самостоятельная и несамостоятельная проводимость газов, 128.37kb.
- Полимерные системы в катализе и электрокатализе возможности и перспективы, 16.03kb.
- Ионная проводимость сложных фосфатов со структурой nasicon а 3-2 X Nb X m 2- X (po, 389.98kb.
- 1. Проводимость (проводник, полупроводник, изолятор, ток, напряжение, сопротивление,, 98.07kb.
- Лекция2 проводимость полупроводников виды проводимости, 502.09kb.
- Кристаллические и стеклообразные фазы в системах biF 3 Bi 2 o 3 BaF, 505.44kb.
- Квч терапии у больных стенокардией, 43.39kb.
- 1. Энергетические зоны и свободные носители заряда в твердых телах. Уровень Ферми, 21.7kb.
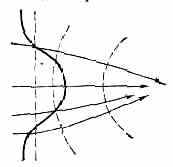
Рис. 4. Изменение хода лучей и самофокусировка света в среде с показателем преломления n, зависящим от интенсивности света; стрелками показан ход лучей; пунктир — поверхности постоянной фазы; сплошная линия — распределение интенсивности света.
Явление самофокусировки обусловлено тем, что в сильном световом поле изменяется показатель преломления среды (в опыте, изображённом на рис. 2 на вклейке к стр. 528, это происходит за счёт нагрева стекла лазерным излучением). Если знак изменения n таков, что область, занятая пучком, становится оптически более плотной, то периферийные лучи отклоняются к центру пучка (на рис. 4 изображены фазовые фронты и ход лучей в ограниченном пучке, распространяющемся в среде, с показателем преломления; n=n0+n2Е2, где n0 — постоянная составляющая, не зависящая от Е, а
460
n2>0. Поскольку фазовая скорость света v=c/n=c/(n0+n2E2), а поле Е на оси больше, чем на периферии, то фазовые фронты изгибаются и лучи отклоняются к оси пучка. Такая нелинейная рефракция может быть столь существенной (её величина нарастает вместе с концентрацией поля), что практически полностью подавляет дифракц. расходимость (см. рис. 3 на вклейке к стр. 528).
В реальном лазерном импульсе мощность изменяется во времени и соответственно изменяется во времени фокальная длина нелинейной линзы. В результате возникает движущийся фокус. Скорость его движения может достигать 109 см/с. Учёт быстрого движения фокусов в сочетании с аберрациями нелинейной линзы во мн. случаях позволяет построить полную теорию явления самофокусировки.
Обратный эффект — с а м о д е ф о к у с и р о в к а возникает, если среда в области, занятой световым пучком, становится оптически менее плотной (n2<0). В этом случае мощный лазерный пучок расходится гораздо быстрее, чем пучок малой интенсивности. Самодефокусировка наблюдается при распространении мощных лазерных пучков в атмосфере. Нелинейные волновые явления типа самофокусировки и самодефокусировки, в к-рых частота почти не изменяется, наз. самовоздействием света (эффекты типа генерации гармоник и смешения волн наз. нелинейными вз-ствиями). Наряду с самовоздействием волн, модулированных в пр-ве, наблюдается также самовоздействие волн, модулированных во времени. Распространение лазерного светового импульса в среде с показателем преломления вида: n= n1+n2E2 сопровождается искажением его формы и фазовой модуляцией.

Рис. 5. Нитевидные разрушения оптич. стекла в поле мощного лазера; тонкая нить — след самофокусиров. светового пучка.
В результате возникает сильное уширение спектра излучения и ширина спектра на выходе из среды в сотни и тысячи раз превышает ширину спектра на входе (самомодуляция). Эффекты самовоздействия определяют осн. черты поведения мощных световых пучков в большинстве сред, включая и активные среды самих лазеров. В частности, лавинное нарастание интенсивности светового поля при самофокусировке вызывает во мн. случаях оптич. пробой среды (рас. 5).
Самопросветление и нелинейное поглощение. Среды, непрозрачные для слабого излучения, могут стать прозрачными для высокоинтенсивного излучения (просветление), и, наоборот, прозрачные материалы могут «затемняться» по отношению к мощному излучению (нелинейное поглощение). Это объясняется зависимостью коэфф. поглощения от интенсивности света. Если интенсивность резонансного (по отношению к поглощающей среде) излучения велика, существенная доля ч-ц среды переходит из основного в возбуждённое состояние и населённости её верх. и ниж. уровней выравниваются. Наступает т. н. насыщение резонансного перехода (стационарное или квазистационарное), в результате к-рого среда перестаёт поглощать, т. е. становится прозрачной для данного резонансного излучения. Именно этот механизм просветления среды изучался в работах Вавилова (см. выше).
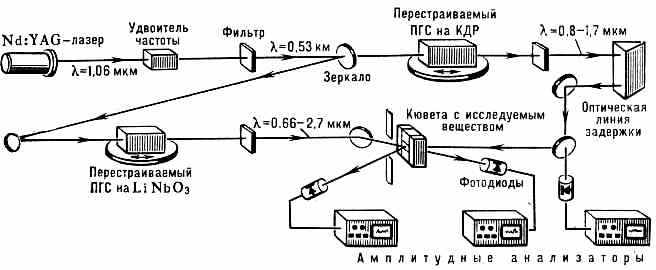
Рис. 6. Схема пикосекундного спектрометра, предназначенного для резонансной спектроскопии первичных стадий процесса фотосинтеза. Сверхкороткие импульсы 2-й гармоники лазера на алюмоиттриевом гранате YAG с примесью Nd (=0,53 мкм) возбуждают два перестраиваемых параметрич. генератора (ПГС) на кристаллах КДР и LiNbO3. Такие генераторы позволяют получить мощные сверхкороткие импульсы длительностью ~1011 с на любой длине волны в диапазоне 0,66—2,7 мкм. При изучении кинетики фотосинтеза генератор на кристалле КДР использовался для селективного возбуждения фотореакц. центров, а другой— для зондирования наведённых изменений поглощения.
Для получения эффекта насыщения в стационарных условиях необходима затрата нек-рой энергии, поэтому просветление среды сопряжено с определёнными потерями энергии светового пучка.
В поле коротких световых импульсов, длительность к-рых меньше характерных времён релаксации среды (для газов ~10-7—10-8с, для конденсиров. сред ~10-11—10-12 с), наблюдается эффект просветления др. типа, наз. эффектом самоиндуцированной прозрачности. В этом случае короткий мощный световой импульс проходит через среду, вообще «не успев» поглотиться (слабое же квазинепрерывное излучение той же частоты может поглотиться этой средой практически полностью). Результатом вз-ствия такого очень короткого светового импульса со средой оказывается резкое уменьшение групповой скорости распространения светового импульса и изменение его формы. Эффекты нелинейного поглощения связаны с тем, что при вз-ствии интенсивного излучения частоты 0 с ч-цами заметную вероятность имеют многофотонные процессы.
Н. о. и нелинейная спектроскопия. Практически все осн. нелинейные оптич. явления (генерация гармоник и смешение частот, самофокусировка, самодефокусировка и самомодуляция лазерных пучков, нелинейное поглощение и просветление, самоиндуцированная прозрачность и т. п.) легли в основу спектроскопич. методов, применяемых для исследования газов, жидкостей и тв. тел — методов нелинейной спектроскопии.
Прикладная Н. о.— круг вопросов, связанных с использованием явлений Н. о. для создания новых источников когерентного оптич. излучения, преобразования частоты, детектирования, преобразования сигналов и изображений. Созданы мощные генераторы на длинах волн =0,34 мкм (2-я гармоника рубинового лазера) и на 2-й гармонике лазера на стекле с примесью Nd. Пром-сть выпускает оптич. умножители частоты, предназначенные для преобразования частоты лазеров на неодимовом стекле или на алюмоиттриевом гранате с примесью Nd (=1,06 мкм), позволяющие получить мощное когерентное излучение на волнах =0,53 мкм (2-я гармоника), =0,35 мкм (3-я гармоника) и =0,26 мкм (4-я гармоника). Для этой цели подобраны кристаллы, обладающие высокой нелинейностью (большими значениями ) и удовлетворяющие условиям фазового синхронизма.
Др. важный класс нелинейных оптич. устройств — перестраиваемые по частоте параметрические генераторы света. В основе их действия лежат нелинейные оптич. явления, связанные с нелинейностью, квадратичной по полю. В среде с поляризацией P=(2)E2 наряду со «слиянием» фотонов
461
(генерацией гармоник и суммарных частот) возможен обратный процесс — когерентный «распад» фотона частоты на два фотона, частоты к-рых 1 и 2 удовлетворяют условию =1+2. Процесс идёт эффективно, если одновременно выполнены условия волнового синхронизма: k=k1+k2. На этом принципе основано действие параметрич. генератора света. При фиксированной частоте (частоте накачки) частоты 1 и 2 можно варьировать в широких пределах (сохраняется лишь их сумма), изменяя параметры среды, влияющие на выполнение условий синхронизма. Параметрич. генератор света — удобный источник перестраиваемых по частоте сверхкоротких световых импульсов. На рис. 6 показана схема пикосекундного спектрометра с двумя параметрич. генераторами света (ПГС), применяемого в биологии. Нелинейные преобразователи частоты используются здесь для изучения процесса трансформации энергии оптич. возбуждения сложными мол. комплексами.
Методы Н. о. открывают новые возможности для создания корреляц. спектрографов и спектрографов с пространств. разложением спектра (см. Спектральные приборы, Фурье спектроскопия). На рис. 7 изображена схема нелинейного спектрографа с пространств. разложением спектра, в котором используется то обстоятельство, что д и с п е р с и я н а п р а в л е н и й с и н х р о н и з м а в нелинейных кристаллах может быть сильнее, нежели обычная дисперсия.
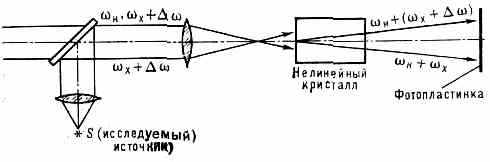
Рис. 7. Схема нелинейного спектрографа с пространств. разложением спектра. Частоты спектр. линий исследуемого источника x+ складываются в нелинейном кристалле с частотой вспомогат. источника (генератора «накачки») н. На выходе кристалла интенсивное излучение суммарной частоты н+х может наблюдаться только внутри весьма узкого угла, для к-рого выполняется условие волнового синхронизма.
Спектральный анализ в этом случае сопровождается увеличением частоты света (что особенно важно при спектр. исследованиях в ИК области) и усилением исследуемого сигнала.
Преобразование сигналов и изображений. Эффект сложения частот, лежащий в основе действия описанного спектрографа, находит также применение при регистрации слабых сигналов в ИК диапазоне. Если частота х лежит в ИК диапазоне, а н — в видимом, то в видимый диапазон попадает и суммарная частота н+х, причём коэфф. преобразования может быть >>1. В видимом же диапазоне
регистрация сигнала производится с помощью высокочувствит. фотоэлектронного умножителя (ФЭУ). Т. о., система из нелинейного кристалла, в к-ром происходит сложение частот, и ФЭУ — чувствительный приёмник ИК излучения, применяемый, напр., в астрономии. Методы Н. о. стали использоваться в адаптивной оптике (см. Обращённый волновой фронт).
Заключение. С ростом напряжённости светового поля обнаруживаются всё новые нелинейные процессы. На первом этапе развития Н. о. использовался диапазон от 1,06 до 0,3 мкм. Переход к ИК-лазерам привёл к открытию нелинейности, связанной с поведением носителей заряда в полупроводниках (в видимом диапазоне она практически не проявляется). При помощи мощных источников УФ излучения стали возможны исследования нелинейного поглощения в диэлектрич. кристаллах с широкой запрещённой зоной и жидкостях, умножение частоты в области вакуумного УФ и мягкого рентгеновского излучения. Уже наблюдались когерентные нелинейные эффекты в рентгеновской области.
Успехи Н. о. стимулировали исследования нелинейных явлений в физике плазмы, акустике, радиофизике и вызвали интерес к общей теории нелинейных волн. В связи с Н. о. появились новые направления исследования в физике тв. тела и жидкостей, связанные с изучением их нелинейных св-в и оптич. прочности.
•Ахманов С. А., Хохлов Р. В., Проблемы нелинейной оптики, М., 1964; Бломберген Н., Нелинейная оптика, пер. с англ., М., 1966; Луговой В. Н., Прохоров А. М., Теория распространения мощного лазерного излучения в нелинейной среде, «УФН», 1973, т. 111, в. 2, с. 203—48; Ахманов С. А., Чиркин А. С., Статистические явления в нелинейной оптике, М., 1971; Цернике Ф., Мидвинтер Дж., Прикладная нелинейная оптика, пер. с англ., М., 1976; Летохов В. С., Чеботаев В. П., Принципы нелинейной лазерной спектроскопии, М., 1975; Келих С., Молекулярная нелинейная оптика, пер. с польск., М., 1981.
С. А. Ахманов.
НЕЛИНЕЙНАЯ ПОЛЯРИЗАЦИЯ, часть поляризации среды, являющаяся нелинейной функцией напряжённости электрич. поля Е, эл.-магн. волны, распространяющейся в среде, и обусловленная негармоничностью отклика элементарного ат. осциллятора на воздействие интенсивного излучения (см. Нелинейная оптика). Квадратичная Н. п. ответственна за детектирование света, генерацию второй гармоники, линейный электрооптич. эффект (см. Поккельса эффект), параметрич. генерацию света (см. Параметрический генератор света). Кубичная Н. п. обусловливает двухфотонное поглощение (см. Многофотонные процессы), генерацию 3-й гармоники, квадратичный электрооптич. эффект (см. Керра эффект), вынужденное комбинационное рассеяние света, вынужденное Мандельштама — Бриллюэна рассеяние, вынужденное рэлеевское рассеяние.
• См. лит. при ст. Нелинейная оптика.
А. В. Андреев.
НЕЛИНЕЙНАЯ СПЕКТРОСКОПИЯ, совокупность методов, в к-рых для исследования строения в-ва служат нелинейные оптич. явления. В Н. с. используются: генерация гармоник и смешение частот, нелинейное поглощение, многофотонные процессы, самоиндуцированная прозрачность, фотонное эхо и т. д. (см. Нелинейная оптика). Методы Н. с. основаны как на наблюдении этих явлений, так и на исследовании их зависимости от параметров излучения: частоты, поляризации, интенсивности, направления распространения и др. Наряду с принципиально новой информацией Н. с. позволяет получить данные, доступные методам традиционной линейной спектроскопии, но с существенно большей точностью, чувствительностью и разрешением. Н. с. даёт информацию о расположении энергетич. уровней, ширинах квантовых переходов и их вероятности, о временах релаксации и т. д. Первые работы по Н. с. появились в 1964— 1966, однако широкое развитие они получили лишь после создания плавно перестраиваемых по частоте лазеров (см. Лазерная спектроскопия) и параметрических генераторов света, излучение к-рых обладает высокой степенью монохроматичности и стабильности.
Важным направлением Н. с. явл. спектроскопия высокого разрешения атомов и молекул. В газах при низком давлении атомы и молекулы испускают и поглощают свет на частотах, смещённых из-за Доплера эффекта относительно собств. частот неподвижных ч-ц. Линии поглощения и излучения ансамбля хаотически движущихся (тепловое движение) ч-ц состоят из множества близких линий, характерных для отд. ч-ц, имеющих определённую скорость, сливающихся в широкую линию (неоднородное уширение). Информация об истинной ширине линий отд. ч-ц (однородная ширина) оказывается замаскированной неоднородным уширением. Кроме того, спектр. линии отд. атомов могут иметь неск. близко расположенных компонентов. Если расстояние между компонентами меньше доплеровской ширины , то структура линии в обычных (линейных) спектрах излучения и поглощения не проявляется. Тем самым теряется информация о тонкой и сверхтонкой структуре квант. уровней атомов и молекул.
462
Для устранения доплеровского уширения и достижения высокого разрешения разработан ряд методов, основанных на нелинейных оптич. явлениях.
В методе д в у х ф о т о н н о й с п е к т р о с к о п и и газ облучается двумя лазерными пучками одинаковой частоты со, распространяющимися навстречу друг другу и способными индуцировать двухфотонные переходы ч-ц с уровня rds1 на уровень
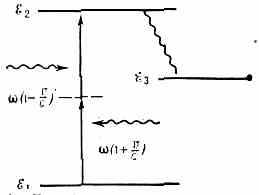
Рис. 1. Двухфотонная спектроскопия на встречных пучках.
ξ2 (рис. 1). Частота перехода неподвижного атома 21=(ξ2-ξ1)/ћ. Атом, движущийся со скоростью v в любом направлении, будет воспринимать частоту одного пучка, смещённую вследствие эффекта Доплера, как (1-v/c), а частоту пучка, распространяющегося в противоположном направлении, как (l+v/c). Если атом поглощает один фотон из одного мучка, а второй — из встречного, то сумма частот воспринимаемых фотонов не зависит от скорости v атома и равна 2. Это означает, что можно наблюдать линию двухфотонного резонанса, свободную от доплеровского уширения. Для регистрации двухфофотонного возбуждения обычно используется люминесценция с возбуждённого уровня ξ2 на промежуточный
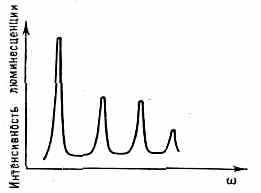
Рнс. 2. Спектр двухфотонного поглощения на встречных пучках (тонкая и сверхтонкая структуры).
Уровень ξ3, интенсивность к-рой пропорц. населённости уровня ξ2. Плавно изменяя частоту , можно получить контур линии двухфотонного поглощения, свободный от доплеровского уширения (рис. 2).
Др. важный метод Н. с.— т. н. с п е к т р о с к о п и я н а с ы щ е н и я, основан на том, что лазерный пучок наиболее сильно взаимодействует только с атомами, скорости к-рых таковы, что частота исследуемого квант. перехода, сдвинутая из-за эффекта Доплера, оказывается в резонансе с падающим излучением.
В результате на контуре доплеровски уширенной линии появляется узкий пик или провал с шириной, равной однородной ширине.
Одно из достижений Н. с.— результаты, полученные методом т. н. ч е т ы р ё х ф о т о н н о й
с п е к т р о с к о п и и, состоящим в смешении трёх волн на нелинейности, кубичной по полю: Р=(3)Е3. Если такую поляризацию возбудить сразу триплетом световых волн с частотами 1, 2, 3, то за счёт нелинейного вз-ствия возникает спектр новых световых волн
с частотами: 4= 1+2+3 4=1+2-3; 4=1-2-3 и т. п.
Это и есть четырёхфотонные процессы (в каждом элем. акте участвуют четыре кванта излучения). Амплитуды волн пропорц. значениям (3) на частотах 4. Если излучения с частотами 1, 2, 3 генерируются лазерами с перестраиваемой частотой, то, исследуя четырёхфотонные процессы,
можно измерять дисперсию (3)(). Метод основан на наблюдении резонансных максимумов в частотной зависимости нелинейной восприимчивости 3-го порядка (3). Это, с одной стороны, даёт новую информацию о в-ве, недоступную традиц. спектроскопии. С другой стороны, данные традиц. спектроскопии (положение и ширина спектр. линий, сечения рассеяния и т. п.) могут быть отсюда получены с большей чувствительностью и лучшим спектр. разрешением. Особенно важна 'дисперсия (3)(),
связанная с процессом вида '4=1+2-3. Резонансы в (3)() (а следовательно, и резонансное увеличение мощности излучения на частоте
'4) возникают, когда либо сами частоты 1, 2, 3, либо их комбинации (1+2 и др.) совпадают с резонансными частотами атомов или молекул. Использование резонансов на суммарной и разностной частотах позволяет изучать резонансные процессы в в-ве в условиях, когда частоты всех световых волн, возбуждающих среду и генерируемых в ней за счёт нелинейных процессов, лежат в области прозрачности. Этот метод позволил с высокой степенью точности исследовать ряд экситонных резонансов в кристаллах (см. Экситон), комбинац. резонансов в газах и конденспров. средах и др. В т. н. нестационарной Н. с. информация извлекается из прямых временных измерений нелинейного отклика квант. системы на возбуждающие световые импульсы. Напр., применение коротких световых импульсов (с длительностью ~10-12 с) в активной спектроскопии комбинационного рассеяния позволяет раздельно измерять времена жизни молекул в возбуждённых состояниях (по затуханию сигнала некогерентного антистоксова рассеяния) а времена релаксации, определяющие ширину линии (по затуханию сигнала рассеяния
в направлении фазового синхронизма, т. е. сигнала когерентного рассеяния),
• Нелинейная спектроскопия, пер. с англ., М., 1979; Летохов В. С., Ч е б о т а е в В. П., Принципы нелинейной лазерной спектроскопии, М., 1975; Ахманов С. А., Коротеев Н. И., Спектроскопия рассеяния света и нелинейная оптика, «УФН», 1977, т. 123, в. 3, с. 405—71; Ахманов С. А., К о р о т е е в Н. И., Методы нелинейной оптики в спектроскопии рассеяния света, М., 1981.
К. Н. Драбович.
