Наведённая проводимость

Вид материала

Документы

Содержание Нелинейная теория поля Нелинейное взаимодействие акустических волн Нелинейные системы Нелокальная теория поля Нелокальное взаимодейст­вие Необратимые процессы Д. Н. Зубарев. Квантовая механика. Непрерывный спектр Неравновесное состояние Неравновесные процессы Неразрывности уравнение S Н. у. даёт закон постоянства расхода Sv=

Подобный материал:

• Электрический ток в газах самостоятельная и несамостоятельная проводимость газов, 128.37kb.
• Полимерные системы в катализе и электрокатализе возможности и перспективы, 16.03kb.
• Ионная проводимость сложных фосфатов со структурой nasicon а 3-2 X Nb X m 2- X (po, 389.98kb.
• 1. Проводимость (проводник, полупроводник, изолятор, ток, напряжение, сопротивление,, 98.07kb.
• Лекция2 проводимость полупроводников виды проводимости, 502.09kb.
• Кристаллические и стеклообразные фазы в системах biF 3 Bi 2 o 3 BaF, 505.44kb.
• Квч терапии у больных стенокардией, 43.39kb.
• 1. Энергетические зоны и свободные носители заряда в твердых телах. Уровень Ферми, 21.7kb.

НЕЛИНЕЙНАЯ ТЕОРИЯ ПОЛЯ, об­щее наименование для квант. теорий поля (КТП), описывающих взаимо­действующие поля. Разл. поля могут взаимодействовать как друг с другом, так и сами с собой (самодействие). Ур-ния взаимодействующих полей всегда нелинейны: линейным ур-ниям соответствуют лишь свободные поля.

Среди Н. т. п. можно выделить два класса: теории, описываемые полино­миальными по полям ур-ниями, к-рые содержат поле лишь в виде степенной ф-ции, и теории, описываемые не­полиномиальными ур-ниями. Послед­ние часто называют существенно не­линейными КТП. В традиц. КТП (в частности, в квант. электродина­мике) обычно использовались поли­номиальные ур-ния. С развитием т. н. динамич. симметрии (см., напр., Киральная симметрия) всё чаще стали использоваться существенно нелиней­ные КТП. Они успешно описывают мн. известные виды вз-ствий элем. ч-ц. Особенно характерна неполино­миальная форма вз-ствия для грави­тации.

Провести строгую с физ. точки зрения границу между полиномиаль­ными и неполиномиальными теориями практически невозможно. Одни и те же виды вз-ствия элем. ч-ц, удов­летворяющие одной и той же динамич. симметрии, могут описываться как полиномиальными КТП, так и неполиномиальными (т. н. линейные и нелинейные реализации динамич. сим­метрии), при этом каждое из описаний имеет свои достоинства и недостатки. Напр., полиномиальная киральная теория (т. н. -модель) ренормируема, однако в ней появляются фиктивные скалярные ч-цы, от к-рых пока не­известно, как избавляться. В неполиномиальных моделях возникают труд­ности с устранением бесконечностей. Обычный метод перенормировок квантовополевой теории возмущений здесь неприменим, и приходится использо­вать спец. способы для получения однозначных результатов. На этом пути уже достигнуты определённые успехи.

В 60—70-е гг. появилось направ­ление, связанное с поисками решений классич. нелинейных и неполиномиальных ур-ний. Вместо обычного пу­ти, т. е. квантования ур-ний линейного приближения и последующего учёта нелинейных членов по теории возму­щений, пытаются учесть нелинейные

463


эффекты ещё до квантования. Оказа­лось, что среди решений нелинейных ур-ний важную роль играют поля, локализованные в небольшой области пр-ва,— т. н. с о л и т о н ы. Эти ре­шения напоминают волн. пакеты, от­вечающие протяжённым ч-цам, и по­этому наз. частицеподобными. Задача квантования солитонных решений представляет значит. трудности.

• В о л к о в М. К., Первушин В. Н., Существенно нелинейные квантовые теории, динамические симметрии и физика мезонов, М. 1978.

М. К. Волков.

НЕЛИНЕЙНОЕ ВЗАИМОДЕЙСТВИЕ АКУСТИЧЕСКИХ ВОЛН в твёрдых телах, одно из проявлений нелиней­ных эффектов, обусловленное тем, что акустич. волна большой (конечной) амплитуды при распространении в тв. теле изменяет его физ. св-ва. Это влияет как на распространение самой волны (самовоздействие, генерация акустич. гармоник, самофокусировка), так и на распространение др. волн в тв. теле (появление волн комбинац. частот, модуляция колебаний и т. д.). При больших смешениях сжатие и растяжение становятся неравноправ­ными: сила отталкивания при сбли­жении атомов нарастает быстрее, чем сила притяжения при увеличении расстояния между атомами (т. е. сжать уже сжатый образец труднее, чем растянуть уже растянутый). В этом случае для описания распространения волн конечной амплитуды необходимо пользоваться нелинейным Гука за­коном и нелинейным волновым ур-нием. При этом возникает зависимость фазовой скорости волны от её ам­плитуды и форма волны по мере её распространения изменяется (сину­соидальная волна может выродиться в пилообразную). Искажение формы волны связано с изменением её спект­ра, к-рый обогащается гармониками. Т. о., нелинейность приводит к гене­рации гармоник в тв. теле. Если же в тв. тело или кристалл излучаются две или большее число акустич. волн одновременно, они будут взаимодей­ствовать друг с другом, порождая новые волны комбинац. частот. Об­разование таких волн (суммарной и разностной частоты) происходит при выполнении условий синхронизма:

₁±₂=₃, k₁±k₂=k₃, (1)

где ₁, ₂, k₁, k₂ и ₃, k₃ — частоты и волновые векторы взаимодейству­ющих и результирующих волн соот­ветственно. Если акустич. волны рас­сматривать как поток фононов, то условия синхронизма можно интерпре­тировать как законы сохранения энер­гии и импульса фононов при вз-ствии:

ћ₁±ћ₂=ћ₃,

ћk₁±ћk₂=ћk₃ (2)

(ћ=h/2, a h — Планка постоянная). Н. в. а. в. можно рассматривать с квант. точки зрения как вз-ствие ко­герентных фононов, т. е. как фонон-фононное вз-ствие.

Для анализа вз-ствия акустич. волн между собой, а также с др. видами волн пользуются методом диспер­сионных диаграмм, при к-ром каждой из волн, участвующих во вз-ствии, сопоставляют вектор (_i, k_i). При выполнении условий синхро­низма три вектора (₁, k₁), (₂, k₂) н (₃, k₃), участвующих во вз-ствии волн, должны составить замкнутый треугольник.

Анизотропия кристаллов приводит к ряду особенностей Н. в. а. в. и генерации акустических гармоник. Так, генерация акустической гармони­ки может проходить с поворотом пло­скости поляризации (см. Кристалла-акустика).

Н. в. а. в. может быть обусловлено геом. нелинейностью, определяемой квадратичным членом в тензоре де­формации; решёточной нелинейностью, связанной с необходимостью в законе Гука учитывать модули упругости 3-го порядка. В пьезоэлектрич. кри­сталлах нелинейные эффекты зависят также от нелинейности пьезоэффекта и от электрострикции. В пьезополупроводниках дополнит. механизмом (часто играющим преобладающую роль перед всеми др. механизмами) явл. электронная (концентрационная) не­линейность (см. Акустоэлектронное взаимодействие). В пьезоэлектрич. кри­сталлах наряду с Н. в. а. в. может иметь место нелинейное вз-ствие аку­стич. и эл.-магн. волн, к-рое обуслов­ливает эффект электроакустич. эха. В случае поверхностных акустических волн (ПАВ) все рассмотренные выше закономерности Н. в. а. в. и генера­ции гармоник сохраняются. Однако имеются нек-рые особенности вслед­ствие неоднородной структуры ПАВ.

Статич. эффекты, состоящие в из­менении параметров акустич. волны под воздействием постоянных или медленно меняющихся механич. и электрич. полей, изучаются в нели­нейной кристаллоакустике. Статич. эффекты служат для управления рас­пространением акустич. волн в тв. телах (напр., для изменения фазы волны), для измерения внутр. напря­жений и гл. обр. для измерения нелинейных коэфф. тв. тел.

Исследование Н. в. а. в. сущест­венно для понимания природы фонон-фононных вз-ствий в тв. телах, опре­деляющих процессы установления теплового равновесия, теплопровод­ности, теплового расширения тв. тел, электропроводности и сверхпроводи­мости. Фонон-фононные вз-ствия иг­рают важную роль в процессах по­глощения УЗ в кристаллах, особенно при низких темп-pax. Н. в. а. в. в тв. телах начинают использовать в уст­ройствах акустоэлектроники для об­работки сигнальной информации.

• 3 а р е м б о Л. К., Красильников В. А., Введение в нелинейную акустику, М., 1966; их же, Нелинейные явле­ния при распространении упругих волн в твердых телах, <-УФН», 1970, т. 102, в. 4.

В. Е. Лямов.

НЕЛИНЕЙНЫЕ СИСТЕМЫ, колеба­тельные системы, св-ва к-рых зависят от происходящих в них процессов. Колебания таких систем описываются нелинейными ур-ниями. Нелинейными явл.: механич. системы, где модули упругости тел зависят от деформаций последних или коэфф. трения между поверхностями тел зависят от относи­тельной скорости этих тел (скорости скольжения); электрические систе­мы, содержащие сегнетоэлектрики, диэлектрич. проницаемость к-рых за­висит от напряжённости электрич. поля, и т. д. Указанные зависимости в механич. системах приводят соот­ветственно либо к нелинейности свя­зей между напряжениями и дефор­мациями (нарушению Гука закона), либо к нелинейной зависимости сил трения от скорости скольжения, либо к нелинейной связи между дейст­вующей на тело силой и сообщаемым ему ускорением (если при этом ско­рость тела меняется по величине). Аналогично в электрич. системах ока­зываются нелинейными: связь между электрич. зарядами и напряжённостью создаваемого ими поля; связь между напряжением на концах проводника и силой протекающего по нему тока (нарушение закона Ома); связь между силой тока и напряжённостью созда­ваемого им магн. поля (магн. индук­цией) в магнетике и др. Каждая из этих нелинейных связей приводит к тому, что дифференциальные ур-ния, описывающие поведение Н. с., ока­зываются нелинейными, откуда и назв. Н. с.

Все физ. системы явл. Н. с. Пове­дение Н. с. существенно отлично от поведения линейных систем. Одна из наиболее характерных особенно­стей Н. с.— нарушение в них супер­позиции принципа. Искажение в Н. с. формы гармонич. внеш. воздействия и неприменимость к Н. с. принципа суперпозиции позволяют осуществ­лять с их помощью генерирование и преобразования частоты эл.-магн. ко­лебаний — выпрямление, умножение частоты, модуляцию колебаний и т. д.

• Горелик Г. С., Колебания и волны, 2 изд., М., 1959, гл. 4; А н д р о н о в А. А., Витт А. А., Xайкин С. Э., Теория колебаний, 2 изд., М., 1959, гл. 2, § 1—4, 6—7, гл. 3, § 1—3, 6—7; П е й н Г., Физика колебаний и волн, пер. с англ., М., 1979.

НЕЛОКАЛЬНАЯ ТЕОРИЯ ПОЛЯ, общее наименование всех обобщений квантовой теории поля (КТП), осно­ванных на предположении о неточечности вз-ствия. Цель Н. т. п.— построение теории, не содержащей УФ расходимостей, присущих локальной КТП.

Имеются две точки зрения на подход к построению Н. т. п. Одна из них состоит в том, что нелокальную тео­рию следует понимать как принци­пиально новую теорию, в к-рой фун­даментальная длина l рассматрива-

464


ется как новая постоянная, такая же универсальная, как скорость света с, заряд эл-на е и постоянная Планка ћ. Постоянная l должна определить мас­штаб расстояний, на к-рых наступают принципиальные изменения в пред­ставлениях о физ. мире (см. Квантование пространства-времени).

Согласно другой точке зрения, Н. т. п. должна описывать нелокаль­ные вз-ствия квантованных полей, не меняя фундам. основ КТП, т. е. не изменяя обычного описания не­взаимодействующих ч-ц. Возникаю­щие параметры размерности длины в этом подходе не явл. универсальными фундам. постоянными, а характери­зуют лишь область нелокального вз-ствия рассматриваемых квантован­ных полей. Самосогласованную, без внутр. противоречий, теорию такого типа удаётся построить с помощью введения нелокальных формфакторов (особого «размазывания» вз-ствия ч-ц по нек-рой области пространства-вре­мени), имеющих определённые матем. св-ва. Это означает, что явления, происходящие на малых расстояниях, могут быть феноменологически опи­саны с помощью нек-рых параметров, имеющих физ. смысл.

• Марков М. А., Гипероны и К-мезоны, М., 1958; Блохинцев Д. И., Про­странство и время в микромире, М., 1970; Ефимов Г. В., Нелокальные взаимодей­ствия квантованных полей, М., 1977.

Г. В. Ефимов.

НЕЛОКАЛЬНОЕ ВЗАИМОДЕЙСТ­ВИЕ, механизм вз-ствия между поля­ми, при к-ром поведение одного поля в какой-либо точке пространства-времени определяется значением др. поля в некоторой окрестности этой точки.

НЕОБРАТИМЫЕ ПРОЦЕССЫ, физич. процессы, к-рые могут самопроиз­вольно протекать только в одном оп­ределённом направлении. К ним от­носятся: диффузия, теплопроводность, термодиффузия, вязкое течение и др., при к-рых происходит направленный пространств. перенос в-ва (диффузия и термодиффузия), теплоты (тепло­проводность), импульса (вязкое те­чение). Все Н. п. явл. не равновесными процессами. Систему, в к-рой про­изошли Н. п., нельзя вернуть в ис­ходное состояние без того, чтобы в окружающей среде не осталось к.-л. изменений. В замкнутых системах Н. п. сопровождается возрастанием энтропии. В открытых системах (к-рые могут обмениваться энергией или в-вом с окружающей средой) при Н. п. энтропия может оставаться постоянной или даже убывать за счёт обмена энтропией с внеш. средой. Однако во всех случаях остаётся положительным производство энтро­пии, т. е. её возрастание в системе за единицу времени из-за наличия Н. п.

Классич. термодинамика, изучаю­щая равновесные (обратимые) процес­сы, для Н. п. устанавливает лишь неравенства, к-рые указывают возможное направление Н. п. (см. Вто­рое начало термодинамики).

• См. лит. при статьях Кинетика физи­ческая и Термодинамика неравновесных про­цессов.

Д. Н. Зубарев.

НЕОПРЕДЕЛЕННОСТЕЙ СООТНО­ШЕНИЕ (неопределённости принцип),

фундаментальное положение квант. теории, утверждающее, что любая физ. система не может находиться в состояниях, в к-рых координаты её центра инерции и импульс одновре­менно принимают вполне определён­ные, точные значения. Количественно Н. с. формулируется след. образом. Если x — неопределённость значе­ния координаты х центра инерции системы, a p_x — неопределённость проекции импульса р на ось х, то произведение этих неопределённостей должно быть по порядку величины не меньше постоянной Планка ћ. Ана­логичные неравенства должны вы­полняться для любой пары т. н. ка­нонически сопряжённых переменных, напр. для координаты у и проекции импульса р_у на ось у, координаты z и проекции импульса p_z. Если под неопределённостями координаты и им­пульса понимать среднеквадратичные отклонения этих физ. величин от их ср. значений, то Н. с. имеют вид:

p_xx ћ /2, p_y yћ/2, .p_zz ћ/2. (1)

Ввиду малости ћ по сравнению с макроскопич. величинами той же раз­мерности действия Н. с. существенны в осн. для явлений атомных (и мень­ших) масштабов и не проявляются в опытах с макроскопич. телами.

Из Н. с. следует, что чем точнее определена одна из входящих в не­равенство величин, тем менее опре­делённо значение другой. Никакой эксперимент не может привести к одновременно точному измерению та­ких динамич. переменных; при этом неопределённость в измерениях свя­зана не с несовершенством эксперим. техники, а с объективными св-вами материи.

Принцип неопределённости, откры­тый в 1927 нем. физиком В. Гейзенбергом, явился важным этапом в вы­яснении закономерностей внутриатом­ных явлений и построении квант. механики. Существ. чертой микроскопич. объектов явл. их корпускулярно-волновая природа (см. Корпускулярно-волновой дуализм). Состояние ч-цы полностью определяется волно­вой функцией. Ч-ца может быть об­наружена в любой точке пр-ва, в к-рой волн. ф-ция отлична от нуля. Поэтому результаты экспериментов по определению, напр., координаты имеют вероятностный хар-р. Это оз­начает, что при проведении серии одинаковых опытов над одинаковыми системами получаются каждый раз разные результаты. Однако нек-рые значения будут более вероятными, чем другие, т. е. будут появляться чаще. Относит. частота появления

тех или иных значений координаты пропорц. квадрату модуля волн. ф-ции в соответствующих точках пр-ва. По­этому чаще всего будут получаться те значения координаты, к-рые лежат вблизи максимума волн. ф-ции. Если максимум выражен чётко (волн. ф-ция представляет собой узкий волновой пакет), то ч-ца в осн. находится около этого максимума. Тем не менее нек-рый разброс в значениях координаты, нек-рая их неопределённость (порядка полуширины максимума) неизбежны. То же относится и к измерению им­пульса.

Т. о., понятия координаты и им­пульса в классич. смысле не могут быть применены к микроскопич. объ­ектам. Пользуясь этими величинами при описании микроскопич. системы, необходимо внести в их интерпретацию квант. поправки. Такой поправкой и явл. Н. с.

Неск. иной смысл имеет Н. с. для энергии ξ и времени t:

ξtћ. (2)

Если система находится в стационар­ном состоянии, то из Н. с. следует, что энергию системы даже в этом со­стоянии можно измерить лишь с точностью, не превышающей ћ/t, где t — длительность процесса из­мерения. Причина этого — во вз-ствии системы с измерит. прибором, и Н. с. применительно к данному случаю означает, что энергию вз-ствия между измерит. прибором и исследуемой си­стемой можно учесть лишь с точностью до ћ/t (в предельном случае мгно­венного измерения возникающий энергетич. обмен становится полностью не­определённым). Соотношение (2) спра­ведливо также, если под ξ понимать неопределённость значения энергии нестационарного состояния замкну­той системы, а под t — характерное время, в течение к-рого существенно меняются ср. значения физ. величин в этой системе.

Н. с. для энергии и времени при­водит к важным выводам относительно возбуждённых состояний атомов, мо­лекул, ядер. Такие состояния неста­бильны, и из Н. с. вытекает, что энергии возбуждённых уровней не могут быть строго определёнными, т. е. обладают нек-рой шириной (т. н. естеств. ширина уровня). Если t — ср. время жизни возбуждённого состоя­ния, то ширина его уровня энергии (неопределённость энергии состояния) составляет ξћ/t. Др. примером служит альфа-распад радиоактивного ядра; энергетич. разброс ξ испу­скаемых -ч-ц связан с временем жизни т такого ядра соотношением: ξћ/.

• См. лит. при ст. Квантовая механика.

О. И. Завьялов.

НЕПЕР (Нп, Np), единица логарифмич. относит. величины (натураль-

465


ного логарифма отношения двух од­ноимённых физ. величин). Названа в честь шотл. математика Дж. Непера (J. Napier). 1Нп=ln│F₂/F₁│ при F₂/F₁=e2,718, где F₂ и F₁ — зна­чения напряжения, силы тока, давле­ния и др. силовых физ. величин. Для энергетич. величин 1 Нп=0,5ln|Р₂/Р₁| при Р₂/Р₁=е², где Р₁, Р₂ — электрич. мощность, плотность анергии и т. п. Ослабление силы тока на 1 Нп соответствует его уменьшению в е2,718 раза, а ослабление электрич. мощности на 1 Нп соответствует её уменьшению в 7,39 раза. 1 Нп=0,8686 бел=8,686 децибел.

НЕПРЕРЫВНЫЙ СПЕКТР, то же, что сплошной спектр.

НЕРАВНОВЕСНАЯ ПЛАЗМА, плаз­ма, состояние к-рой не является со­стоянием полного термодинамич. рав­новесия. Примерами Н. п. могут быть: 1) т. н. «неизотермич.» плазма, в к-рой темп-pa эл-нов отличается от темп-ры ионов; 2) плазма, пространственно неоднородная, в частности ограничен­ная магн. полем; 3) плазма, содер­жащая отд. направленные потоки эл-нов или ионов. Как правило, не­равновесность плазмы приводит к её неустойчивости, проявляющейся в на­растании возмущений и «раскачке» волн разл. типов.

В. А. Трубников.

НЕРАВНОВЕСНОЕ СОСТОЯНИЕ, в термодинамике — состояние системы, выведенной из равновесия термодина­мического, в статистич. физике — из состояния статистич. равновесия. В си­стеме, находящейся в Н. с., происхо­дят необратимые процессы, к-рые стре­мятся вернуть систему в состояние термодинамич. (или статистич.) рав­новесия, если нет препятствующих этому факторов — отвода (или под­вода) энергии или в-ва из системы (в систему). В противном случае воз­можно стационарное Н. с. (не изме­няющееся со временем). Н. с. изуча­ются термодинамикой неравновесных процессов и статистич. теорией нерав­новесных процессов (кинетикой фи­зической).

Д. Н. Зубарев.

НЕРАВНОВЕСНЫЕ ПРОЦЕССЫ в термодинамике и статистической фи­зике, физ. процессы, включающие не­равновесные состояния. Пример: про­цесс установления равновесия (тер­модинамич. или статистич.) в изоли­рованной системе, находящейся в неравновесном состоянии. Если в такой системе существуют неоднород­ное поле темп-р, градиенты концент­раций и скоростей упорядоченного движения ч-ц, то вызванные ими Н. п. теплопроводности, диффузии, вязкого течения будут способствовать устра­нению различия св-в в разных частях системы и установлению равновесия. В н е и з о л и р о в а н н ы х систе­мах Н. п. могут протекать стацио­нарно (без изменений физ. состояния системы, пример — теплопередача при

пост. разности темп-р за счет тепло­проводности). Н. п. явл. необратимы­ми процессами, связанными с произ­водством энтропии.

Д. Н. Зубарев.

НЕРАЗРЫВНОСТИ УРАВНЕНИЕ, одно из ур-ний гидродинамики, выра­жающее закон сохранения массы для любого объёма движущейся жидкости (газа). В переменных Эйлера (см. Эйлера уравнения гидродинамики) Н. у. имеет вид:



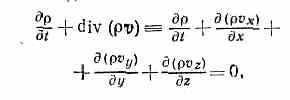
где  — плотность жидкости, v — ее скорость в данной точке, a v_x, v_y, v_z — проекции скорости на координатные оси. Если жидкость несжимаема (=const), H. у. принимает вид:



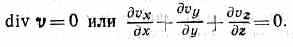
Для установившегося одномерного те­чения в трубе, канале и т. п. с пло­щадью поперечного сечения S Н. у. даёт закон постоянства расхода Sv=const.