Наведённая проводимость

Вид материала

Документы

Содержание Нуклонные изобары Нулевая энергия Нулевой звук Нулевой метод измерений К. П. Широков. Нуссельта число Эйлеровы углы). Ньютона законы механики Ньютона кольца Рис. 1. Кольца Ньюто­на в отражённом свете. А., П. Гагарин. НЬЮТОНОВСКАЯ ЖИДКОСТЬ (вяз­кая жидкость)

Подобный материал:

• Электрический ток в газах самостоятельная и несамостоятельная проводимость газов, 128.37kb.
• Полимерные системы в катализе и электрокатализе возможности и перспективы, 16.03kb.
• Ионная проводимость сложных фосфатов со структурой nasicon а 3-2 X Nb X m 2- X (po, 389.98kb.
• 1. Проводимость (проводник, полупроводник, изолятор, ток, напряжение, сопротивление,, 98.07kb.
• Лекция2 проводимость полупроводников виды проводимости, 502.09kb.
• Кристаллические и стеклообразные фазы в системах biF 3 Bi 2 o 3 BaF, 505.44kb.
• Квч терапии у больных стенокардией, 43.39kb.
• 1. Энергетические зоны и свободные носители заряда в твердых телах. Уровень Ферми, 21.7kb.

НУКЛИДЫ, общее назв. ат. ядер, отличающихся числом нейтронов N и протонов Z, Н. с одинаковыми Z и разными N наз. изотопами.

НУКЛОННЫЕ ИЗОБАРЫ, то же, что барионные резонансы с нулевой стран­ностью.

НУКЛОНЫ (от лат. nucleus — ядро), общее наименование для протонов и нейтронов — ч-ц, из к-рых построены все ядра атомные. См. также Изото­пическая инвариантность.

НУЛЕВАЯ ЭНЕРГИЯ, разность меж­ду энергией осн. состояния квантовомеханич. системы и энергией, соот­ветствующей минимуму потенц. энер­гии системы. Существование Н. э. явл. следствием неопределённостей соот­ношения. В классич. механике счи­талось, что ч-ца может находиться в точке, отвечающей минимуму по­тенц. энергии, обладая одновременно нулевой кинетич. энергией. В этом случае ч-ца находится в состоянии устойчивого равновесия и имеет миним. энергию, равную потенц. энергии в точке равновесия. Вследствие квантовомеханич. соотношения неопреде­лённостей для координаты (х) и им­пульса (р): px ~ ћ локализация ч-цы (x0) вблизи минимума по­тенциала приводит к большому зна­чению ср. кпнетич. энергии ч-цы из-за большого разброса в значениях импульса (p ~ ћ/x). С другой сто­роны, уменьшение степени локали­зации ч-цы (x0) приводит к уве­личению ср. потенц. энергии, т. к. ч-ца проводит значит. время в об­ласти пр-ва, где потенциал превышает миним. значение. Энергия осн. уровня соответствует наименьшей возможной энергии квантовомеханич. системы, совместимой с соотношением неопреде­лённостей.

Наличие Н. э.— общее св-во свя­занных систем микрочастиц. Система не может перейти в состояние с энер­гией, меньшей Н. э., без изменения

своей структуры.

С. С. Герштейн.

НУЛЕВОЙ ЗВУК, особого рода коле­бания, к-рые могут распространяться в квант. жидкостях (ферми-жидкостях, напр. в жидком ³Не) при темп-pax, очень близких к абс. нулю. Н. з. связан с отклонением ф-ции распре­деления существующих в ферми-жид­кости элем. возбуждений (квазичастиц) от равновесного значения. Скорость Н.. з. с₀ не совпадает со скоростью обычного звука с, к-рая определяется сжимаемостью жидкости, причём с₀>с. Н. з. был предсказан Л. Д. Ландау (1957) на основе общей теории ферми-жидкости, экспериментально обнару­жен в жидком ³Не амер. физиками в 1966. В температурном интервале от 2 до 100 мК и давлении 0,32 атм ср. значение с составило 187,9 м/с, а с₀=194,4 м/с (на частотах 15,4 и 45,5 МГц). Н. з. может возникать также в металлах, эл-ны в к-рых об­разуют заряженную ферми-жидкость.

• Абель В. Р., А н д е р с о н А. К., У и т л и Дж. К., Распространение нуле­вого звука в жидком Не³ при низких тем­пературах, пер. с англ., «УФН», 1967, т. 91, в. 2. См. также лит. при ст. Квантовая жидкость,

НУЛЕВОЙ МЕТОД ИЗМЕРЕНИЙ, одна из разновидностей метода срав­нения с мерой, в к-рой на нулевой прибор воздействует сигнал, пропорц. разности между измеряемой величиной и известной величиной, причём эту разность доводят до нуля. Для вое-

472


произведения физ. величин определ. размера, служащих для сравнения, в Н. м. и. применяют меры этих вели­чин. Примеры Н. м. и.: измерения массы при помощи гирь на рычажных весах, измерения электрич. величин (эдс, напряжения, ёмкости, сопро­тивления и др.), а также неэлектрич. величин, преобразованных в электри­ческие (темп-ры, давления, деформа­ций и т. д.) с применением потенцио­метров и измерит. мостов (см. также Компенсационный метод измерений). Уравновешивание прибора сравнения может быть автоматизировано.

• Маликов С. Ф., Тюрин Н. И., Введение в метрологию, 2 изд., М., 1966; Карандеев К. Б., Специальные методы электрических измерений, М.—Л., 1963.

К. П. Широков.

НУЛЕВОЙ ПРИБОР (нуль-индикатор), прибор для обнаружения неравенства сравниваемых величин при нулевом методе измерений. В качестве Н. п. могут применяться гальванометры, электрометры, электронно-лучевые трубки и др. устройства.

НУССЕЛЬТА ЧИСЛО [по имени нем. физика В. Нуссельта (W. NuSelt)], безразмерный параметр, характеризу­ющий интенсивность конвективного теплообмена между поверхностью те­ла и потоком газа (жидкости) в случае вынужденной и естественной конвек­ции. Н. ч. Nu=l/, где =Q/TS — коэфф. теплообмена, Q — кол-во теп­лоты, отдаваемой (или получаемой) поверхностью тела в единицу времени, T>0 — разница между темп-рой поверхности тела и темп-рой газа (жидкости) вне пограничного слоя, S — площадь поверхности, I — ха­рактерный размер,  — коэфф. тепло­проводности газа.

НУТАЦИЯ (от лат. nutatio — коле­бание), происходящее одновременно С прецессией движение тв. тела, при к-ром изменяется



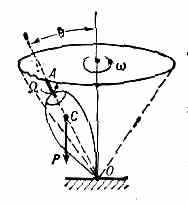
угол между осью собств. вращения тела и осью, во­круг к-рой проис­ходит прецессия; этот угол наз. углом Н. (см. Эйлеровы углы). У гироскопа (волч­ка) , движущегося под действием си­лы тяжести Р (рис.), Н. представляет собой колебания оси гироскопа, ам­плитуда и период к-рых тем меньше, а частота тем больше, чем больше угловая скорость его собств. вращения . При больших  амплитуда ₁-₀ и период  Н. приближённо равны:



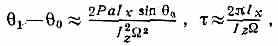
где ₀ и ₁ — пределы изменения угла Н. , а — расстояние от неподвижной точки до центра тяжести, I_z — мо­мент инерции гироскопа относительно его оси симметрии, I_x — момент инер­ции относительно оси, перпендикулярной к оси симметрии и проходящей через неподвижную точку.

Под Н. гироскопич. системы (механич. системы, содержащей гиро­скоп) понимают то периодич. изме­нение углов, определяющих положе­ние системы, к-рое происходит с малыми амплитудами и большими частотами. Из-за наличия сопротив­лений (трения) нутац. колебания до­вольно быстро затухают, после чего гироскоп (или гироскопич. система) совершает чисто прецессионное дви­жение, С. М. Тарг.

НЬЮТОН (Н, N), единица СИ силы. Названа в честь англ. учёного И. Нью­тона (I. Newton). 1 Н — сила, сооб­щающая телу массой 1 кг ускорение 1 м/с² в направлении действия силы.

1 Н=10⁵ дин=0,102 кгс.

НЬЮТОНА ЗАКОН ТЯГОТЕНИЯ (всемирного тяготения закон), см. в ст. Тяготение.

НЬЮТОНА ЗАКОНЫ МЕХАНИКИ, три закона, лежащие в основе т. н. классич. механики или механики Нью­тона. Сформулированы И. Ньютоном (1687). Первый закон: «Всякое тело продолжает удерживаться в сво­ём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние». Второй закон: «Из­менение количества движения про­порционально приложенной движу­щей силе и происходит по направ­лению той прямой, по которой эта сила действует». Третий закон: «Действию всегда есть равное и про­тивоположное противодействие, ина­че, взаимодействия двух тел друг на друга между собой равны и направ­лены в противоположные стороны». Н. з. м. появились как результат обоб­щения многочисл. наблюдений, опы­тов и теоретич. исследований итал. учёного Г. Галилея, голл. учёного X. Гюйгенса, И. Ньютона и др.

Согласно совр. представлениям и терминологии, в первом и втором за­конах под телом следует понимать материальную точку, а под движе­нием — движение относительно инер­циальной системы отсчёта. Матем. выражение второго закона в классич. механике имеет вид:

d(mv)dt=F или тw=F,

где m — масса точки, v— её ско­рость, w — ускорение, t — время, F — действующая сила (см. Дина­мика).

Н. з. м. перестают быть справедли­выми для движения объектов очень малых размеров, сравнимых с раз­мерами атомов (напр., элем. ч-цы), и при движениях со скоростями, близкими к скорости света. См. Кван­товая механика, Относительности те­ория.

• Галилей Г., Беседы и математические доказательства, касающиеся двух новых от­раслей науки, относящихся к механике и местному движению, Соч., [пер. с лат.], т. 1,

М.—Л., 1934; Ньютон И., Математичес­кие начала натуральной философии, пер. с лат., в кн.: Крылов А. Н., Собр. тру­дов, т. 7, М.—Л., 1936. См. также лит. при ст. Механика.

С. М. Тарг.

НЬЮТОНА КОЛЬЦА, интерференци­онные полосы равной толщины в форме колец, расположенных концентриче­ски вокруг точки касания двух сферич. поверхностей либо плоскости и сферы. Впервые описаны в 1675 И. Ньютоном. Интерференция света происходит в тон­ком зазоре (обычно воздушном), разде­ляющем соприкаса­ющиеся поверхнос­ти; этот зазор играет роль тонкой плёнки (см. Оптика тонких слоев).




Рис. 1. Кольца Ньюто­на в отражённом свете.

Н. к. наблюдаются и в проходящем, и — более отчётливо — в отражённом свете. При освещении монохроматич. светом длины волны  Н. к. представляют собой чередующие­ся тёмные и светлые полосы (рис. 1). Светлые возникают в местах, где разность фаз между прямым и дважды отражённым лучом (в проходящем свете) или между лучами, отражён­ными от обеих соприкасающихся по­верхностей (в отражённом свете), рав­на 2n (n=1, 2, 3, ...) (т. е. разность хода _m равна чётному числу полу­волн). Тёмные кольца образуются там, где разность фаз равна (2n+1). Разность фаз лучей определяется тол­щиной зазора _m с учётом изменения фазы световой волны при отражении (см. Отражение света). Так, при отражении от границы воздух — стек­ло фаза меняется на л, а при отра­жении от границы стекло — воздух фаза остаётся неизменной. Поэтому в случае двух стеклянных поверхностей (рис. 2), с учётом различий в условиях отражения от нижней и верхней поверхности зазора (потеря полуволны), m-е тёмное кольцо образуется, если _m=2_m+/2=(2m+1)/2, т. е. при толщине за­зора _m=m/2.



Рис. 2. Схема обра­зования колец Нью­тона: О — точка ка­сания сферич. ра­диуса R и плоской поверхности; _m — толщина возд. за­зора в области об­разования кольца


Радиус r_m m-го кольца определяется из треугольника А'О'С: r_m=R²-(R-_m)² 2R_m. Откуда r_m=(2R_m), а для тёмного m-го кольца r_m=(Rm). Это соот­ношение позволяет с хорошей точ­ностью определятьпо измерениям

473


r_m. Если  известна, Н. к. можно использовать для измерения радиусов поверхностей линз и контроля пра­вильности формы сферич. и плоских поверхностей. При освещении не­монохроматическим (напр., белым) све­том Н. к. становятся цветными. Наи­более отчётливо Н. к. наблюдаются при малой толщине зазора (т. е. при использовании сферич. поверхностей больших радиусов).

• Шишловский А. А., Прикладная физическая оптика, М., 1961; Дитчберн Р., Физическая оптика, пер. с англ., М., 1965. А., П. Гагарин.

НЬЮТОН-МЕТР (Н•м, N•m), еди­ница СИ момента силы и момента пары сил. 1 Н•м —момент силы, равной

1 Н, относительно точки, располо­женной на расстоянии 1 м от линии действия силы. 1 Н•м=10⁷ дин•см=0,102 кгс•м.

НЬЮТОНОВСКАЯ ЖИДКОСТЬ (вяз­кая жидкость), жидкость, подчиняю­щаяся при своём течении закону вяз­кого трения Ньютона (1684). Для прямолинейного ламинарного течения этот закон устанавливает наличие ли­нейной зависимости (прямой пропор­циональности) между касательным на­пряжением  в плоскостях соприкос­новения слоев жидкости и производ­ной от скорости течения v по направ­лению нормали n к этим плоскостям, т. е. =dv/dn, где — динамич. коэфф. вязкости. В общем случае пространств.

течения для Н. ж. имеет место ли­нейная зависимость между тензорами напряжений и скоростей деформации. Св-вами Н. ж. обладают большинство жидкостей (вода, смазочное масло и др.) и все газы. Течение Н. ж. изу­чается в гидроаэромеханике. Жидкости, для к-рых указанные выше зависи­мости не явл. линейными, наз. н е н ь ю т о н о в с к и м и. К ним отно­сится, напр., ряд суспензий и р-ров полимеров. Течение неньютоновских жидкостей изучается в реологии.

НЬЮТОН-СЕКУНДА (Н•с, N•s), еди­ница СИ импульса силы. 1 Н•с — импульс силы, равной 1 Н и дейст­вующей в течение 1 с. 1 Н•с=10⁵ дин•с=0,102 кгс•с.