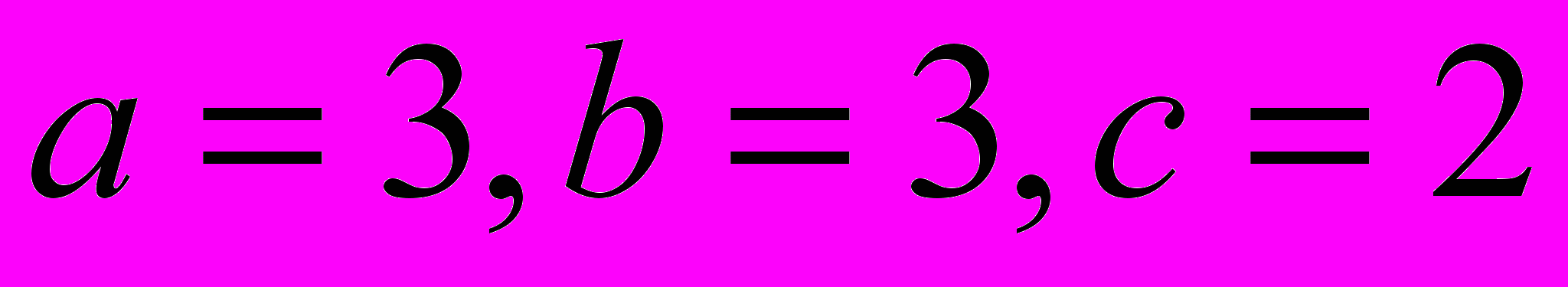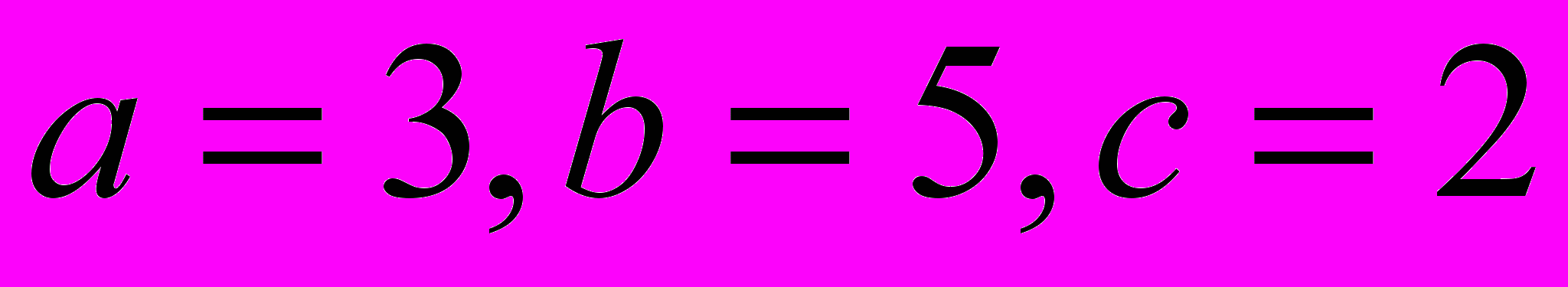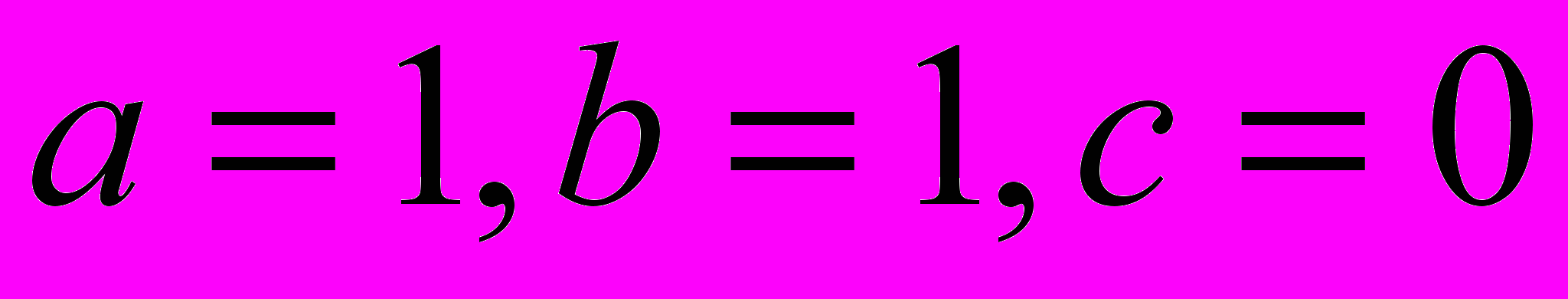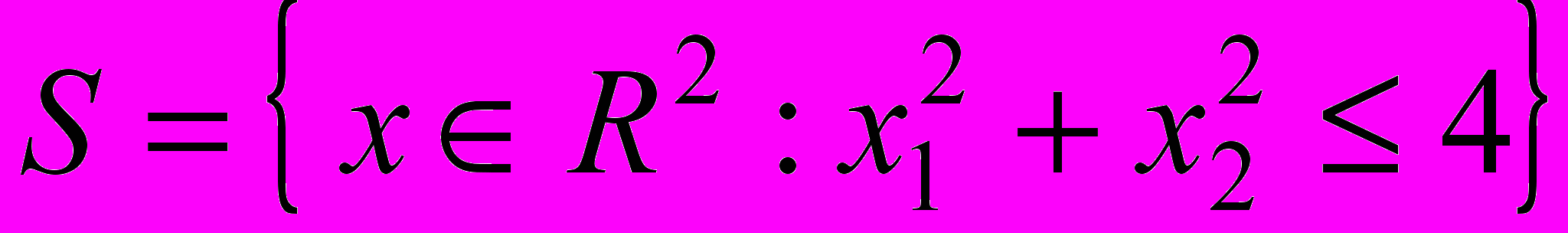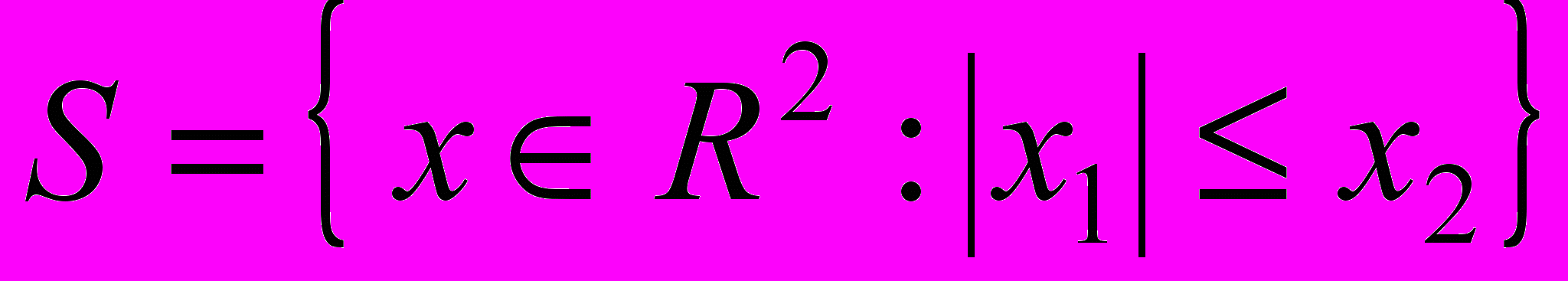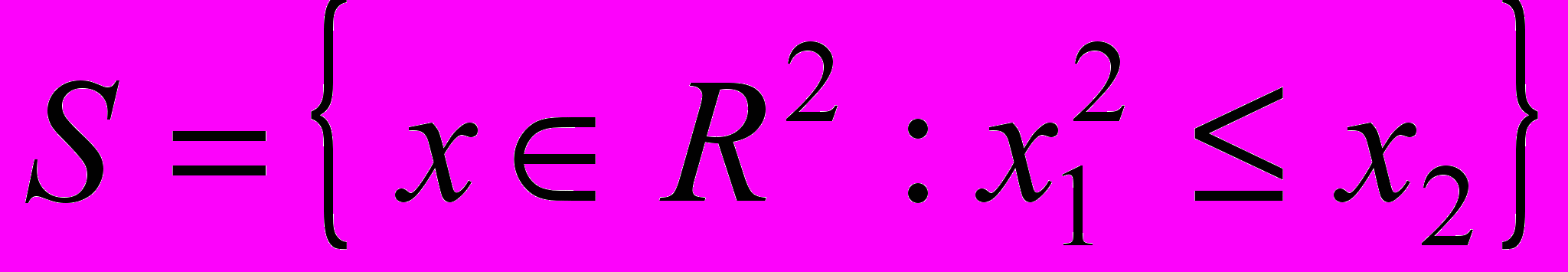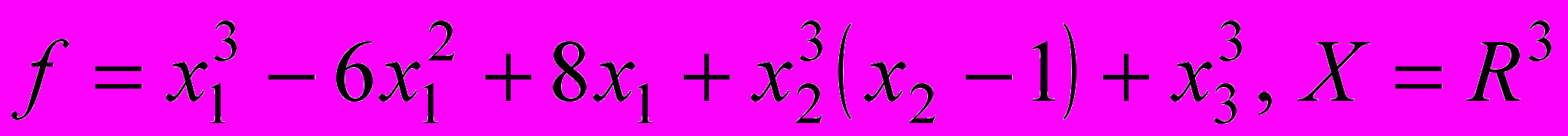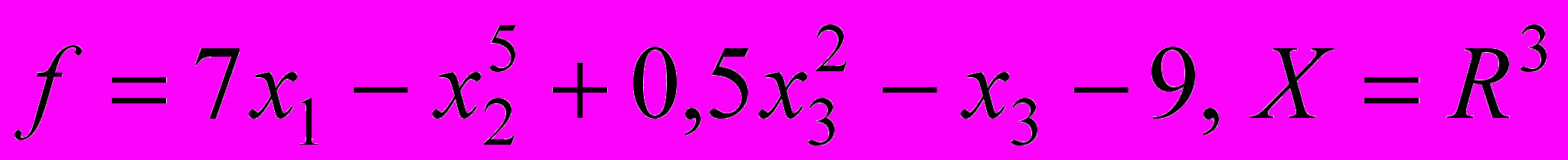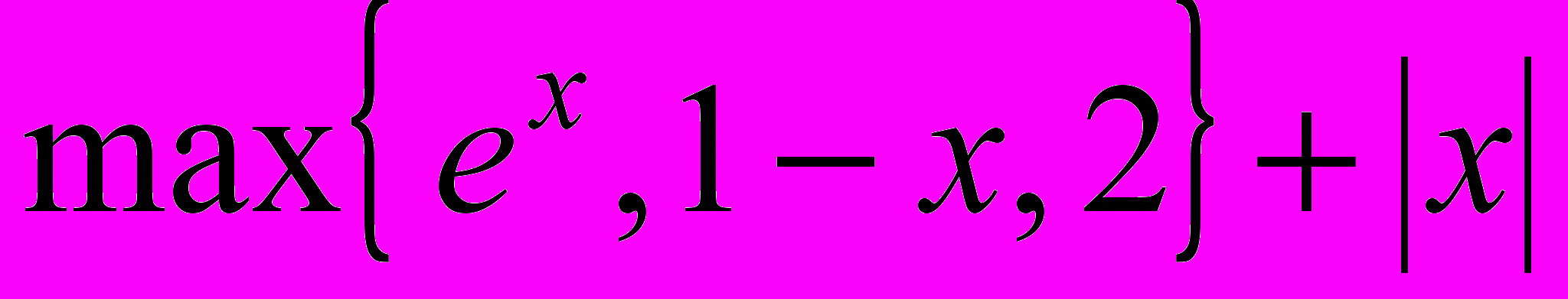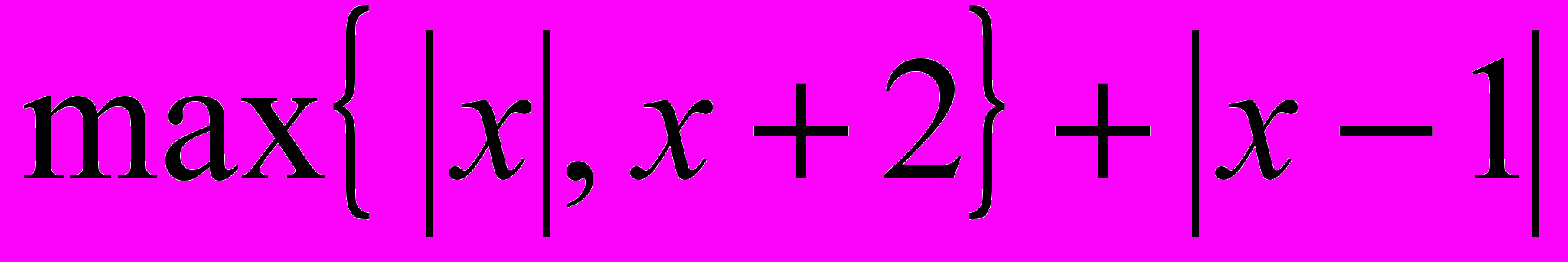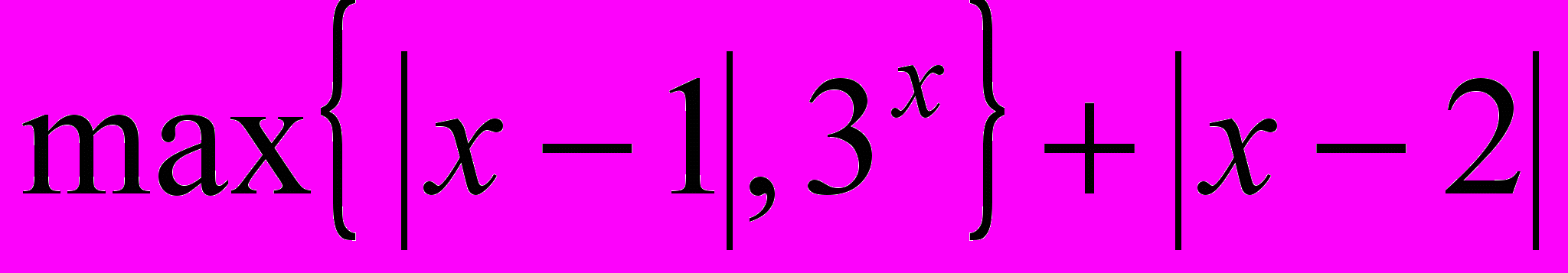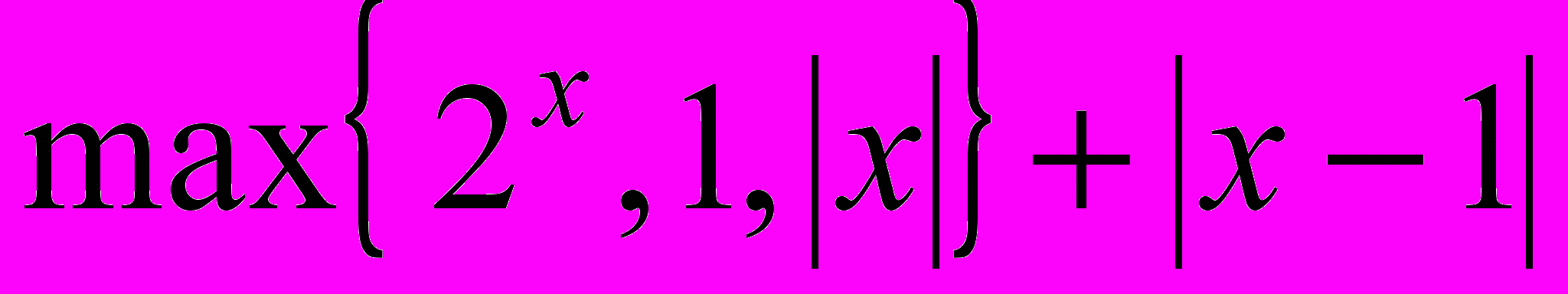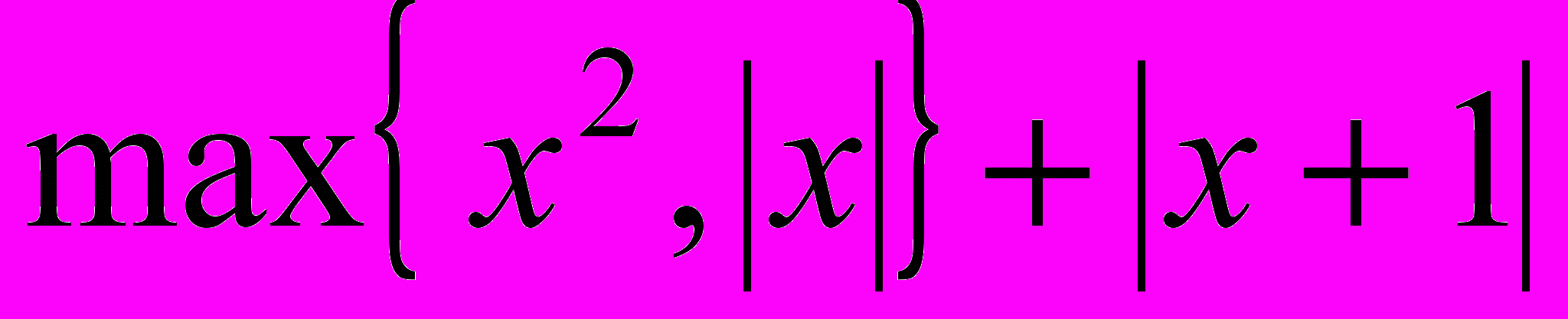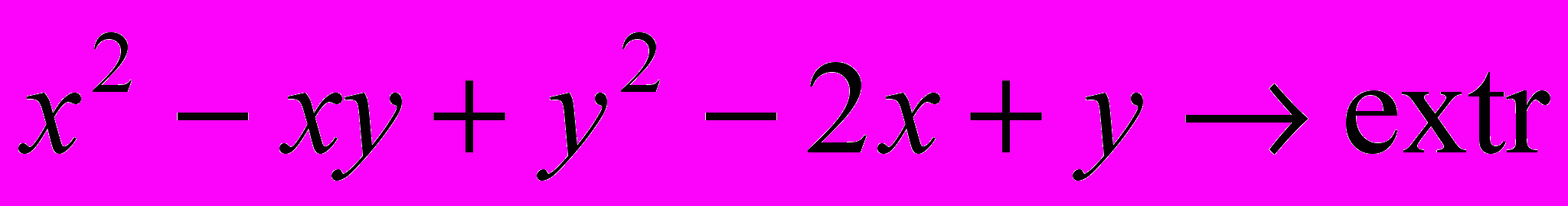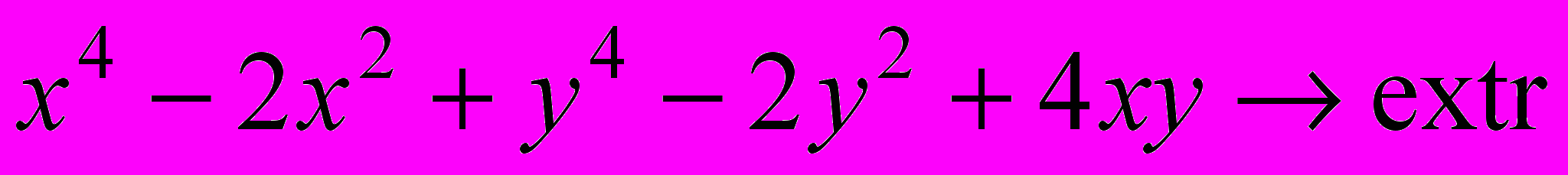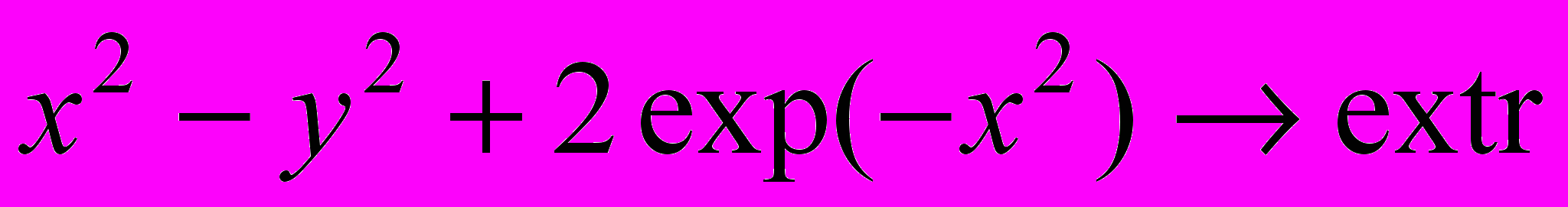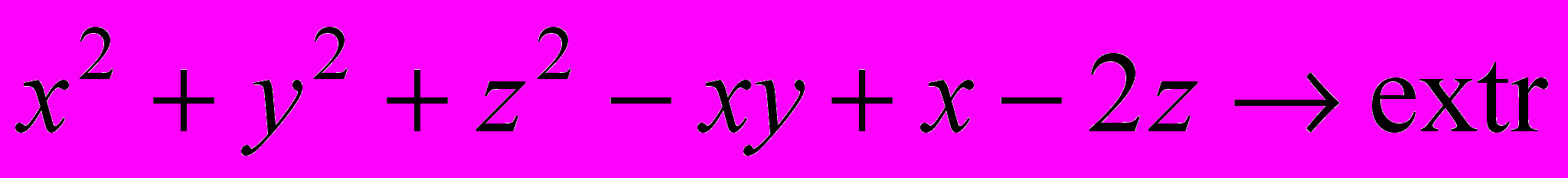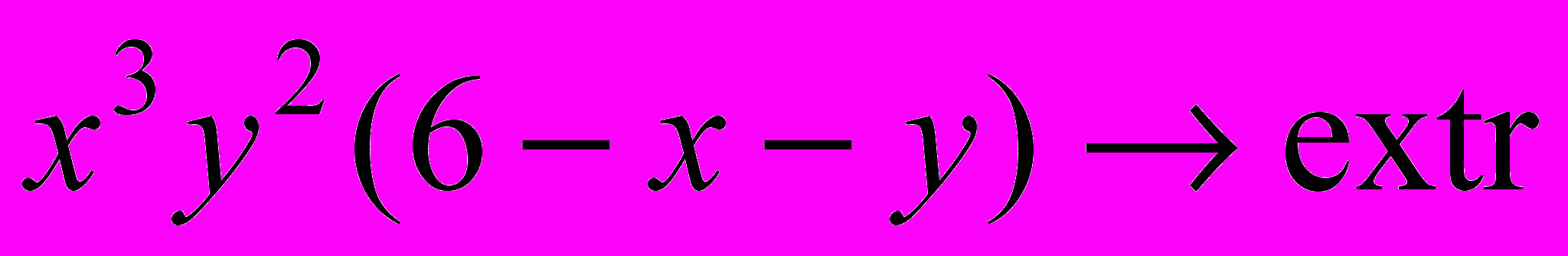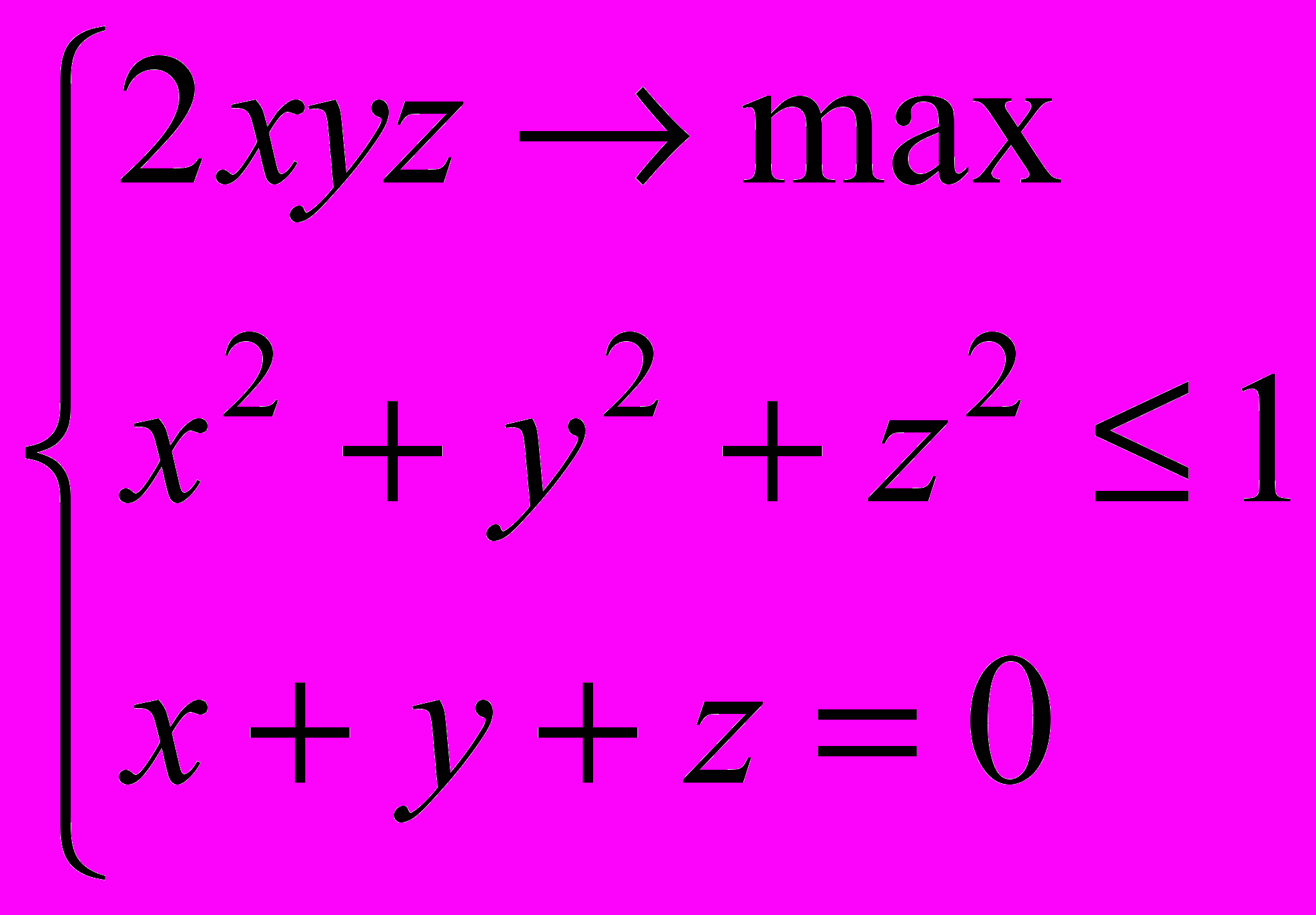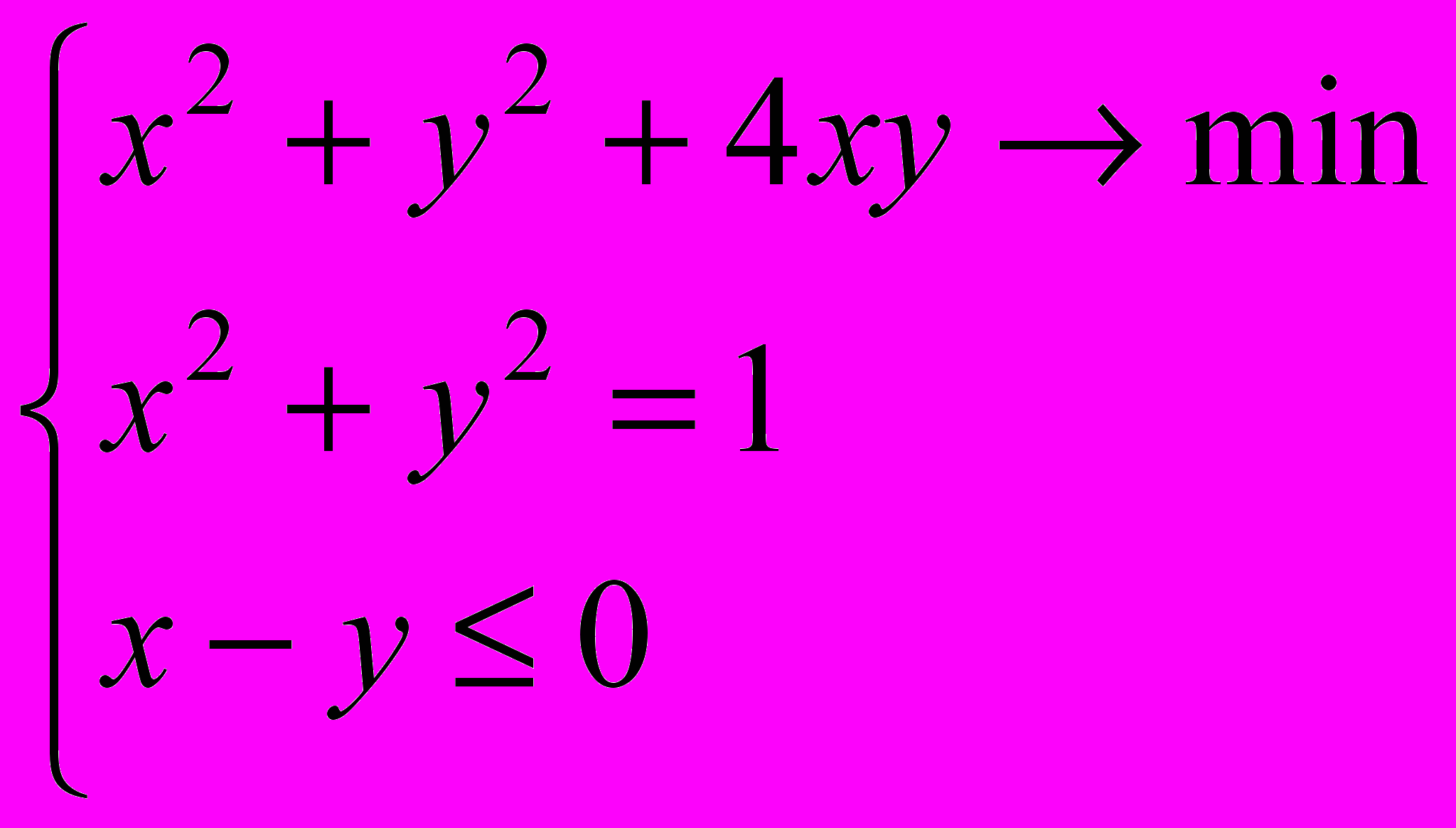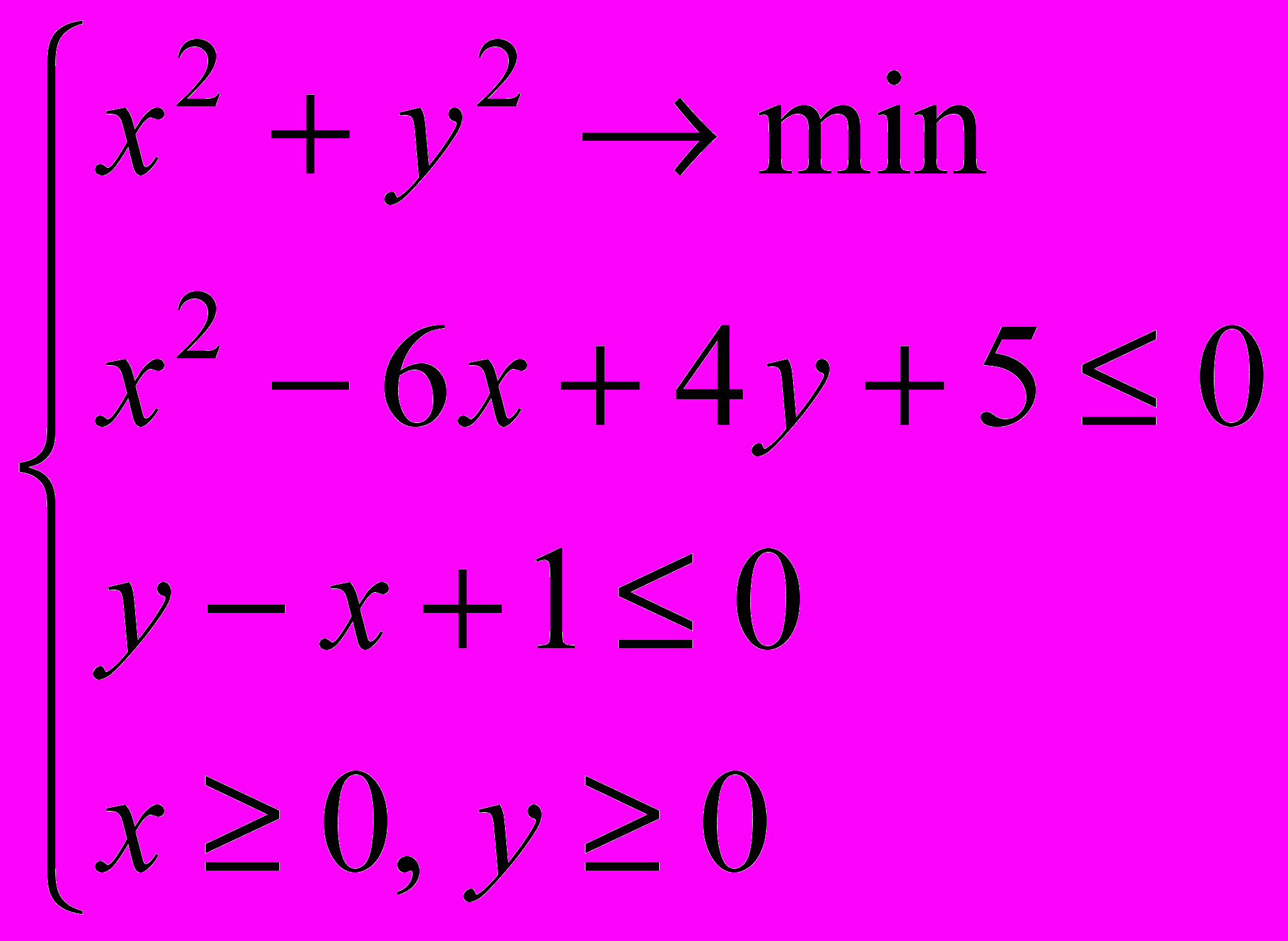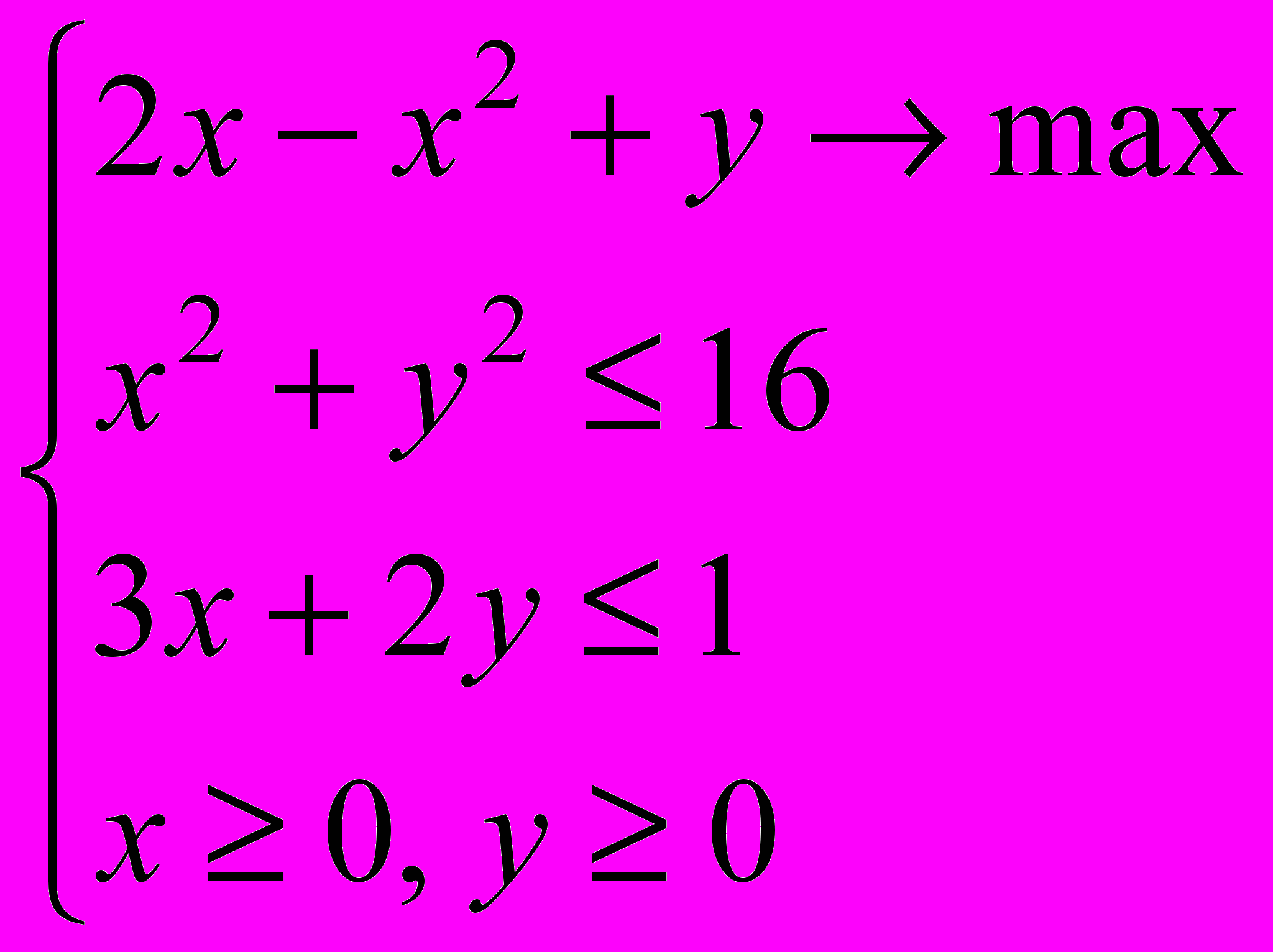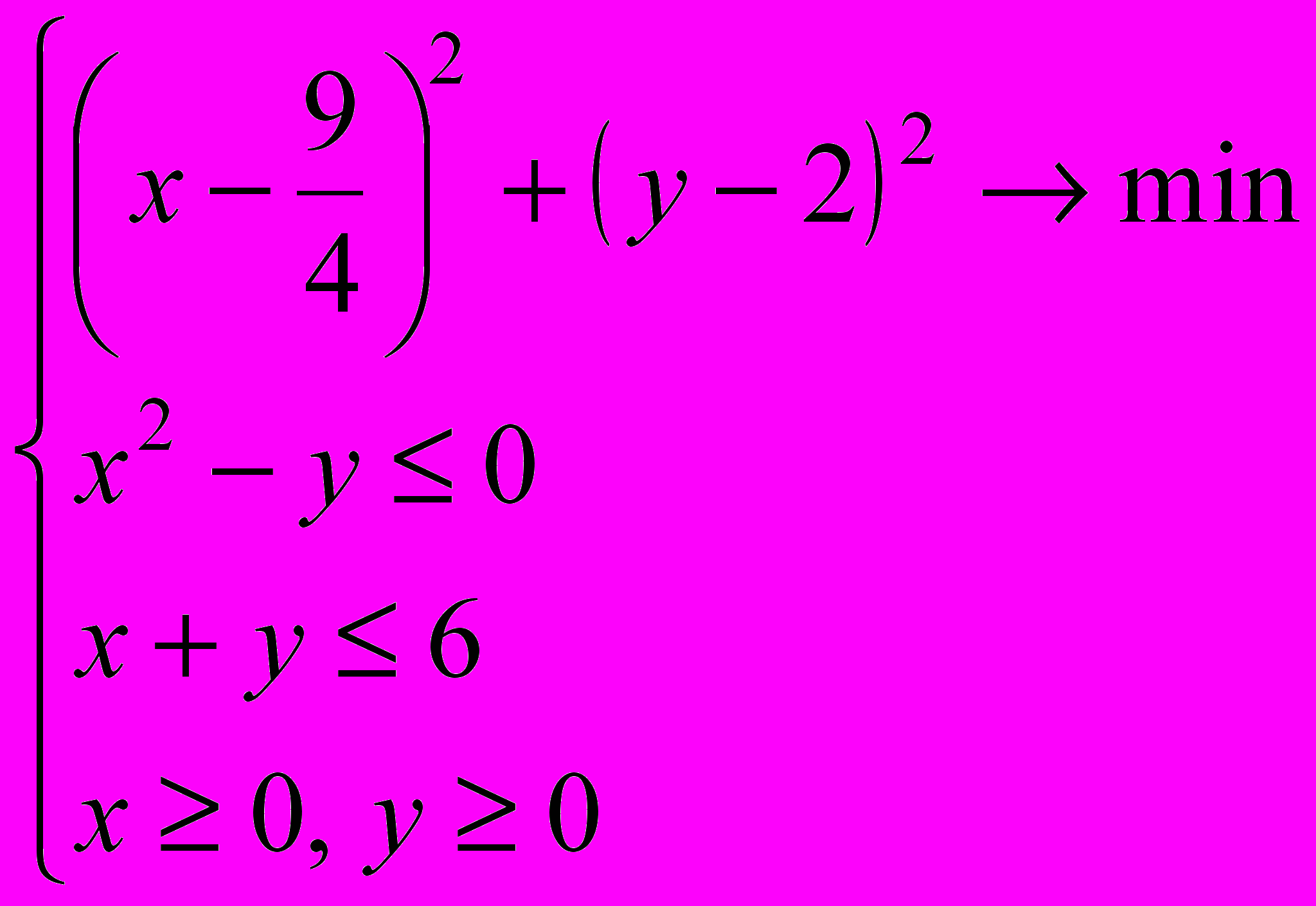Контрольная работа по учебной дисциплине «Методы оптимизации»
| Вид материала | Контрольная работа |
СодержаниеПеречень вопросов к экзамену по учебной дисциплине «Методы оптимизации» |
- Контрольная работа № по дисциплине: (Полное название учебной дисциплины), 41.88kb.
- Календарный план учебных занятий по дисциплине Компьютерный дизайн оптических наноструктур,, 39.38kb.
- Контрольная работа по дисциплине «Макроэкономика 2» выполняется студентом на основе, 303.53kb.
- Учебной дисциплины «Методы оптимизации» для направления 010400. 62 «Прикладная математика, 40.12kb.
- Отчет по дисциплине «методы оптимизации и принятия решения» на тему «лабораторная работа, 23.84kb.
- Рабочая программа учебной дисциплины (модуля) методы оптимизации, 164.09kb.
- Рабочая учебная программа по дисциплине «Методы оптимизации» Направление №230100 «Информатика, 129.28kb.
- Контрольная работа по дисциплине Тема, 80.19kb.
- Контрольная работа по дисциплине «Оперативно финансовая работа» на тему: «Внутреннее, 151.27kb.
- Повторение. Аналитические методы оптимизации функций одной и нескольких переменных, 250.23kb.
Контрольная работа по учебной дисциплине «Методы оптимизации»
- Изобразить на плоскости сумму двух множеств:
 , где
, где 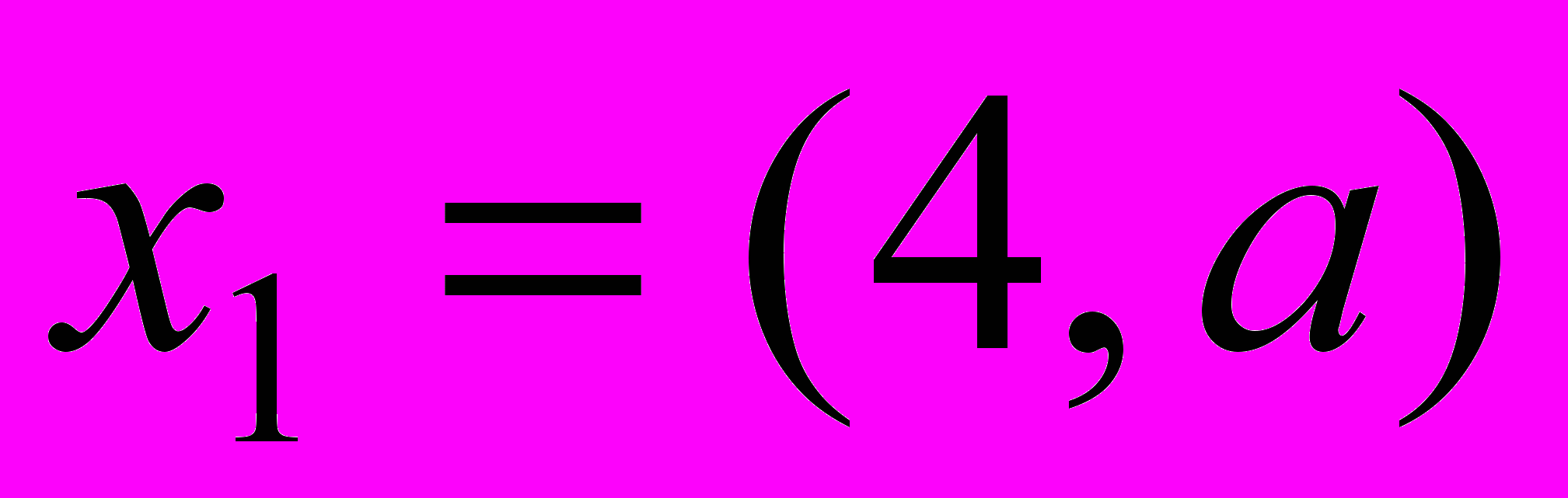 ,
, 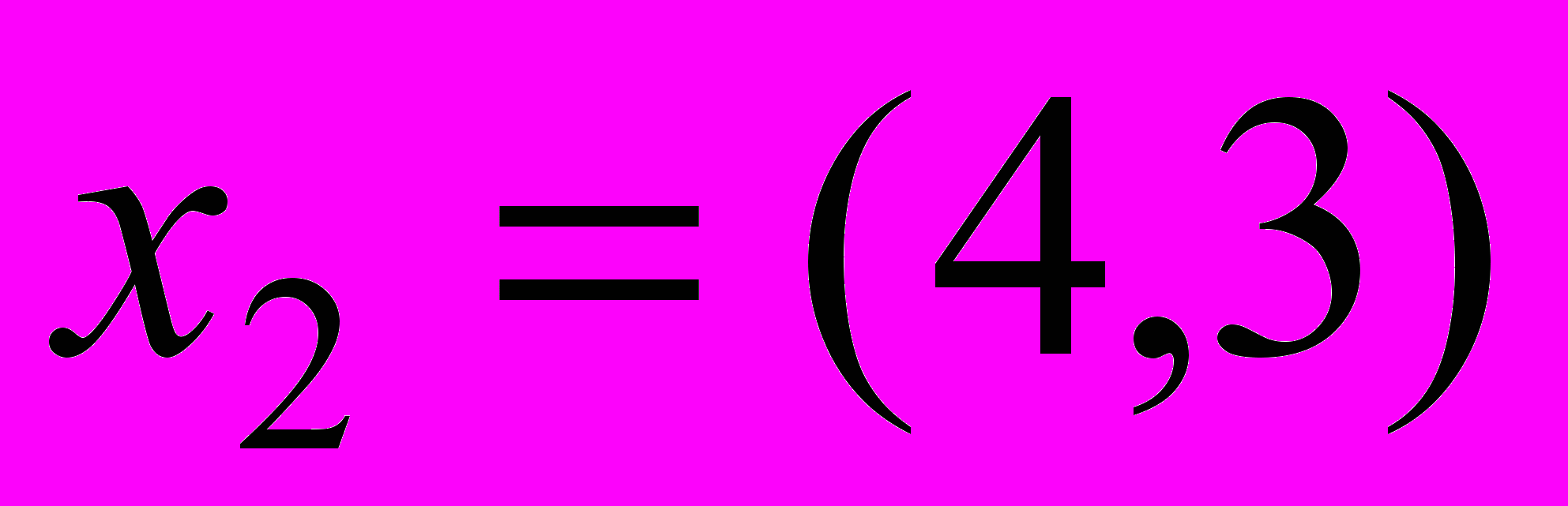 и
и 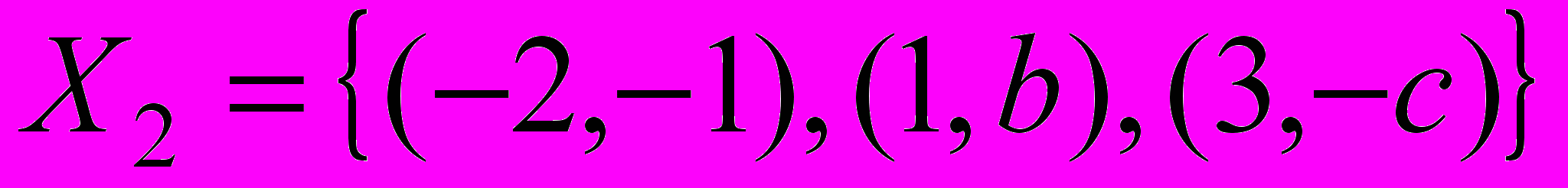
-
- Доказать выпуклость множества
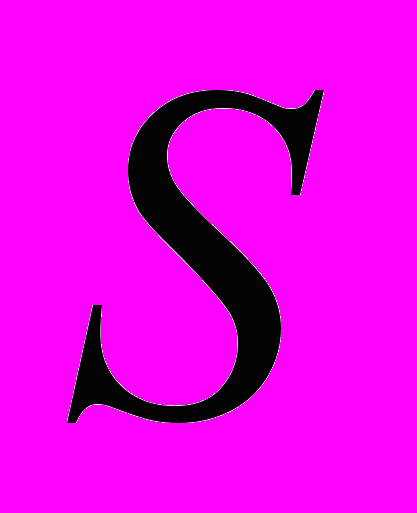 :
:
-
- Проверить является ли функция
 выпуклой (вогнутой) на заданном множестве
выпуклой (вогнутой) на заданном множестве 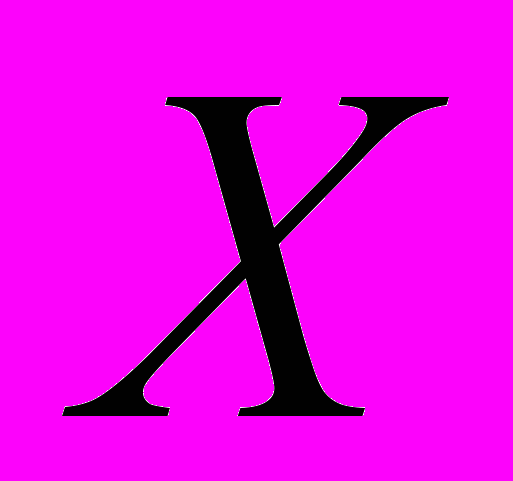 , указать такие точки из
, указать такие точки из 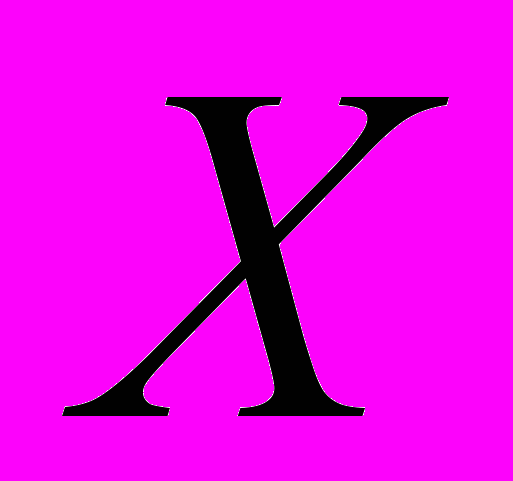 , в окрестности которых
, в окрестности которых  не является ни выпуклой, ни вогнутой:
не является ни выпуклой, ни вогнутой:
-
- Доказать выпуклость функции
 и вычислить ее субдифференциал:
и вычислить ее субдифференциал:
-
- Решить задачу безусловной оптимизации:
-
- Решить задачу условной оптимизации, используя метод множителей Лагранжа:
-
- Решить задачу условной оптимизации, используя теорему Куна-Таккера:
-
Перечень вопросов к экзамену по учебной дисциплине
«Методы оптимизации»
- Постановка задачи оптимизации. Понятие локального и глобального минимумов. Классификация задач оптимизации. Примеры задач оптимизации.
- Теоремы существования в задачах оптимизации.
- Определение выпуклого множества. Теоремы о выпуклости пересечения и суммы выпуклых множеств с произвольными коэффициентами.
- Выпуклая комбинация точек. Теорема о выпуклой комбинации точек выпуклого множества.
- Лемма о выпуклости множества всех выпуклых комбинаций точек произвольного множества.
- Выпуклая оболочка множества. Теорема о выпуклой оболочке множества. Критерий выпуклости множества.
- Понятие разделяющей гиперплоскости. Теорема о разделяющей гиперплоскости.
- Понятие опорной гиперплоскости. Теорема о существовании опорной гиперплоскости к выпуклому множеству.
- Теорема об отделимости выпуклых множеств.
- Понятие надграфика и эффективной области функции. Собственные функции. Определение выпуклой функции. Необходимое и достаточное условие выпуклости собственной функции. Теорема о выпуклости эффективной области выпуклой функции.
- Определение строго выпуклой и сильно выпуклой функции на выпуклом множестве. Теорема о выпуклости суммы двух выпуклых функций с неотрицательными коэффициентами.
- Неравенство Йенсена (критерий выпуклости функции). Теорема о максимуме выпуклых функций. Теоремы о суперпозиции выпуклых функций.
- Понятие производной по направлению. Теорема о существовании производных по направлению выпуклой функции. Теорема Радемахера.
- Критерий сильной выпуклости дважды непрерывно дифференцируемой функции. Критерий выпуклости дважды непрерывно дифференцируемой функции. Достаточное условие строгой выпуклости.
- Теоремы о свойствах множества точек минимума выпуклой функции.
- Понятие субдифференциала функции. Геометрическая интерпретация. Свойства субдифференциала выпуклой функции. Теорема Кларка.
- Понятие направления убывания функции. Понятие возможного направления. Теорема о необходимых условиях минимума в терминах направлений.
- Теоремы о дифференциальных условиях оптимальности функции на многомерном параллелепипеде и на множестве векторов с неотрицательными компонентами.
- Функция Лагранжа. Теорема о достаточных условиях абсолютного минимума в задачах условной оптимизации.
- Понятие регулярной задачи оптимизации. Условие регулярности и его геометрический смысл.
- Условие регулярности Слейтера. Теорема Куна-Таккера. Теорема Куна-Таккера в дифференциальной форме.
- Понятие седловой точки. Теорема о седловой точке функции Лагранжа (достаточное условие оптимальности). Теорема о существовании седловой точки функции Лагранжа.
- Основная схема численных методов безусловной оптимизации. Критерии останова. Понятие сходимости метода. Скорость сходимости. Классификация численных методов оптимизации.
- Способы выбора шага по направлению.
- Градиентные методы решения задач безусловной оптимизации. Понятие плохо обусловленной (овражной) функции. Особенности градиентных методов.
- Метод Ньютона решения задач безусловной оптимизации. Модификации метода Ньютона.
- Сопряженные направления и их использование для решения задач безусловной минимизации выпуклых квадратичных функций. Методы сопряженных градиентов. Особенности методов.
- Субградиентные методы. Особенности методов.
- Метод проекции градиента. Теорема о необходимом и достаточном условии оптимальности в задачах выпуклого программирования. Особенности метода.
- Метод штрафных и барьерных функций для решения задач условной оптимизации.
Замечание: вопросы 24-30 являются дополнительными.
Лектор________________ доцент кафедры ТУиО, к. ф.-м. н. Алеева С.Р.