Geum.ru

Физическая

Вид материалаРабочая программа
Поверхностные явления. Адсорбция.
Таблица 1 Стандартные электродные потенциалы ()
Подобный материал:
1   2   3   4   5   6   7   8   9

Поверхностные явления. Адсорбция.


Изучение поверхностных свойств является одной из важных проблем химии.

Запас свободной поверхностной энергии А определяется суммарной поверхностью частиц S и коэффициентом поверхностного натяжения :

А=S (Дж/м2).

При отсутствии стабилизатора свободная поверхностная энергия коллоидной системы понижается за счет уменьшения величины поверхности S (происходит коагуляция).

Чтобы предотвратить агрегирование частиц, добавляют стабилизатор, который при неизменной величине поверхности снижает свободную поверхностную энергию, уменьшая поверхностное натяжение .

Величина поверхностного натяжения  численно равна работе, которую необходимо затратить на образование 1м2 новой поверхности в изотермических условиях (Дж/м2 или Н/м). Известно несколько методов определения поверхностного натяжения.

Метод поднятия жидкости в капилляре:

 = h r  g (Н/м) ,

2

где: r- радиус капилляра (м);

 - плотность (кг/м3);

g - ускорение силы тяжести (м/сек2).


Метод Траубе - с помощью сталагмометра подсчитывается какое число капель стандартной жидкости no и исследуемой жидкости nx содержится в определенном объеме жидкостей :

n0x0

= ,

nx0

где : 0 и x - плотности стандартной и исследуемой жидкостей;

0 - поверхностное натяжение стандартной жидкости.

Для измерения поверхностного натяжения растворов можно применять также метод «отрыва кольца». Кольцо из металлической проволоки опускается на поверхность жидкости и уравновешивается рычагом весов. Затем определяется усилие, которое нужно приложить, чтобы преодолеть силу сцепления кольца с жидкостью и оторвать кольцо от поверхности

F = k (Н/м) ,

где : k - обобщающая константа, зависящая от диаметра проволоки, размеров кольца и краевого угла смачивания Θ .

Широко распространен метод наибольшего давления пузырька, предложенный П.А.Ребиндером. К поверхности жидкости подводится вакуумная пробирка с капилляром, на конце которого под действием вакуума образуется воздушный пузырек. Давление, при котором пузырек проскакивает через поверхностную пленку жидкости и прорывает ее, определяется величиной x :

0 рx

x= (Н/м) ,

р0

где : 0 - поверхностное натяжение стандартной жидкости (Н/м);

рx и р0 - давления, необходимые для проскакивания пузырька через поверхность исследуемой и стандартной жидкостей (Н/м2).

Поверхностно-активными называются вещества, добавки которых уменьшают поверхностное натяжение растворителя. По отношению к воде - это органические кислоты, спирты, белки, мыла и др. дифильные (т.е. состоящие из полярной и неполярной частей) вещества.

Изменение поверхностного натяжения раствора при введении ПАВ определяют с помощью уравнения Шишковского:

0 -  = а ln (1+bС) ,

где : 0 - поверхностное натяжение растворителя (Н/м) ;

 - поверхностное натяжение раствора (Н/м) ;

a и b - эмпирические константы, причем величина а мало меняется от вещества к веществу, а b зависит от поверхностной активности вещества;

С - концентрация раствора (кмоль/м3).

Мерой поверхностной активности вещества является константа b в уравнении Шишковского.

Введение ПАВ, понижающих поверхностное натяжение, сопровождается увеличением концентрации растворенного вещества в поверхностном слое или на поверхности раздела фаз - адсорбция.

Для определения адсорбции применяются:

1)уравнение Гиббса :

С d

Г =  ,

RT dC

где : Г - адсорбция (кмоль/м2);

С - концентрация раствора (кмоль/м3) ;

R - газовая постоянная ;

Т - температура , К ;

d

- мера поверхностной активности.

dC
  1. уравнение монослойной адсорбции Ленгмюра:

bC

Г=Г (кмоль/м2) ,

1+bC

где : Г - предельное количество адсорбирующегося вещества ;

b - константа, характеризующая поверхностную активность вещества;

С - равновесная концентрация растворенного вещества (кмоль/м3).

Константы Г и b можно найти графически, преобразовав уравнение Ленгмюра в уравнение прямой :

1 1 1 1

= · + .

Г Гb C Г

Используя уравнение Шишковского, можно перейти от уравнения Гиббса к уравнению Ленгмюра :


d аb С d ab C

= ; Г =  = 

dC 1+bC RT dC 1+bC RT

а bC а

или Г=  , очевидно = Г ,тогда

RT 1+bC RT

bC

Г = Г ;

1+bC
  1. при адсорбции газа или растворимого вещества на твердом адсорбенте используют эмпирическое уравнение Фрейндлиха:

Г =С (для растворов) или Г=р (для газов).

Для вычисления константы  и , достаточно прологарифмировать уравнение Фрейндлиха (lgГ=lgβ +αlgC) и построить прямую в координатах lgГ = (lgC), где отрезок, отсекаемый этой прямой от оси ординат будет равен lgβ, а тангенс угла наклона прямой равен α .

4) уравнение для расчета полислойной адсорбции (уравнение Дубинина). Изотерма адсорбции на адсорбентах с мелкими порами

(Гср.  10-9м) - они получили название адсорбентов первого структурного типа - имеет вид:

Г= (/v)*e - k,T lg ( p /p),

а для крупнопористых адсорбентов второго структурного типа

(Гср.10-7-10-6м):

Г= (/v)*e - k T lg ( p /p),

где : Г - адсорбция (кмоль/кг);

 - общая пористость (м3/кг);

V - молярный объем адсорбируемого вещества в жидком состоянии

(м3/кмоль);

Т - температура (К) ;

k1 и k2 - константы ;

р - равновесное давление пара при данной температуре (Н/м2) ;

рS - давление насыщенного пара (по справочнику) (Н/м2).

При логарифмировании уравнение легко переходит в линейную форму, откуда графически определяется пористость сорбентов.

Для построения кривых распределения пор сорбентов по радиусам применяют метод капиллярной конденсации : экспериментально определяют величину адсорбции в зависимости от увеличения равновесного давления, а затем определяют величину десорбции при снижении равновесного давления. На графике в координатах Г = (р/рS) кривые адсорбции и десорбции не совпадают- образуется петля гистерезиса. Истинному ходу процесса сорбции отвечает ветвь десорбции; ее и используют для расчета пористости (м3/кг):

 = Г V ,

где: Г - экспериментальная величина сорбции (кмоль/кг);

V - молярный объем вещества (по справочнику) (м3/кмоль).

Для определения радиусов пор применяют уравнение Томсона:

2V

r = --------------- (м),

RT ln(ps /p)

где:  - поверхностное натяжение конденсата при данной температуре (Дж/м2) (по справочнику);

V - молярный объем конденсата (по справочнику) (м3/кмоль);

R - газовая постоянная ;

рS - давление насыщенного пара над макроповерхностью (Н/м2) (по справочнику);

р - равновесное давление в капилляре данного радиуса (Н/м2) (по кривой десорбции).

Интегральная кривая строится в координатах =(r), а дифференциальная - в координатах (/r)=ср, где :

м = м+1 - м ; r = rм+1 - rм ; rср - средний радиус, равный

rсрм = (rм+1 + rм)/2. Процессы ионного обмена на твердой поверхности характеризуется уравнением Б.П.Никольского:

Г1(1/Z ) С1(1/Z )

= К ,

Г2(1/Z ) С2(1/Z2 )

где Г1 и Г2 - количество ионов, поглощенных поверхностью сорбента (кмоль/кг) ;

С1 и С2 - равновесные концентрации ионов в растворе (кмоль/м2);

К - константа обмена, зависящая от способности ионов к адсорбции на данном сорбенте. Графически изображается прямой, тангенс угла наклона которой и представляет величину константы К.


Пример. По экспериментальным данным постройте кривую адсорбции углекислого газа на цеолите при 2930К и с помощью графического метода определить константы уравнения Ленгмюра:

Равновесное давление

Р∙10-2, н/м2
1,0
5,0
10,0
30,0
75,0
100,0
200,0

Адсорбция

Г∙103, кмоль/кг

35,0
86,0
112,0
152,0
174,0
178,0
188,0


Решение. По данным таблицы строится кривая адсорбции CO2 на цеолите.

Г·103 ,кмоль/кг

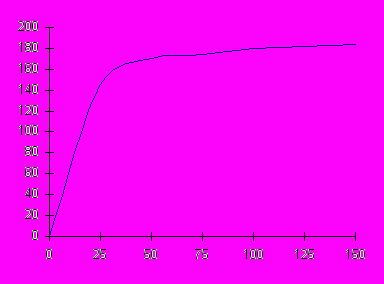р·10-2,н/м2

Уравнение монослойной адсорбции Ленгмюра имеет вид: Г=Г∞ ∙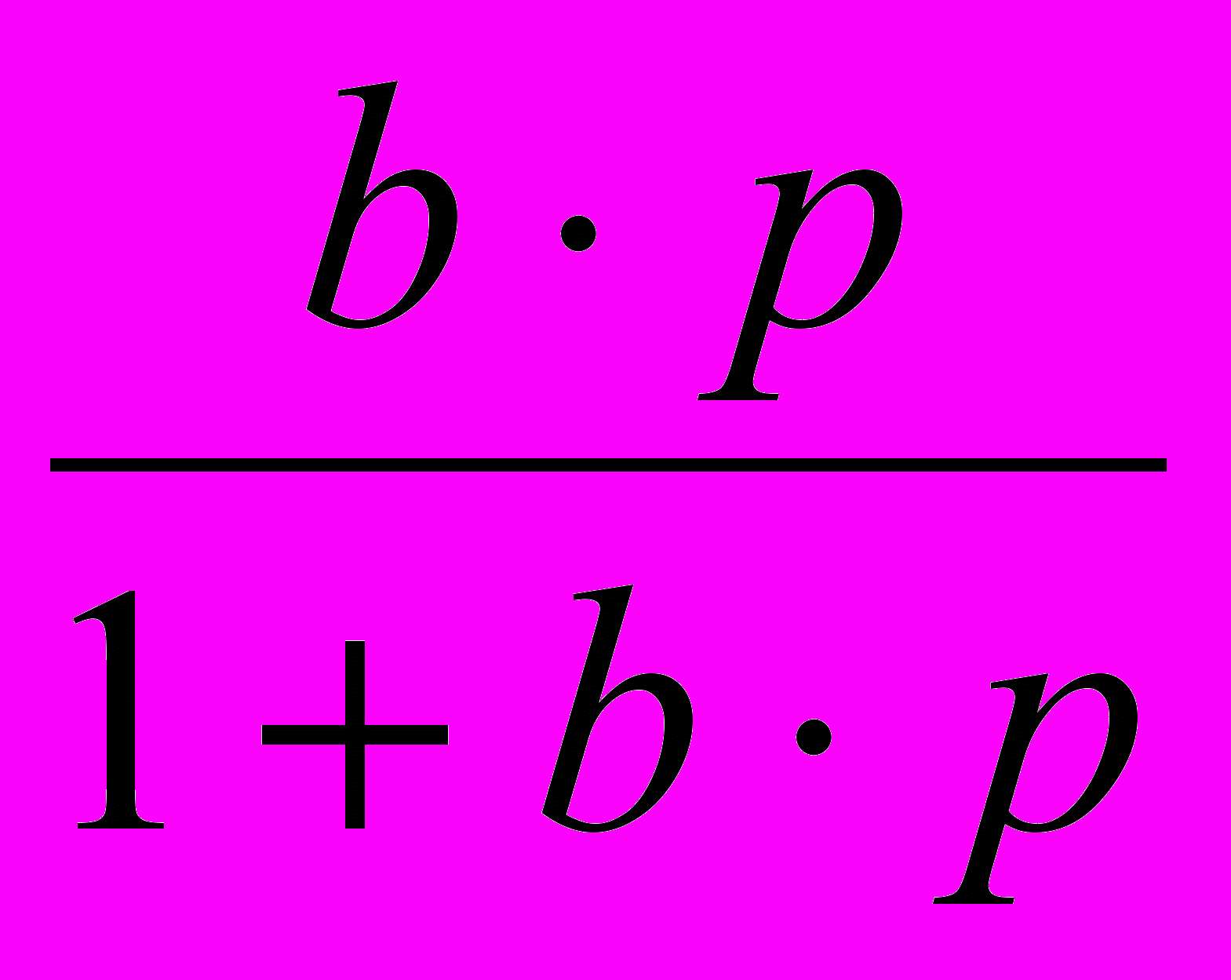, где

Г∞ - предельное количество адсорбируемого вещества; b – константа, характеризующая поверхностную активность вещества; р – равновесное давление растворенного вещества.

Константы Г∞ и b находят графически, преобразуя уравнение Ленгмюра в уравнение прямой: делят единицу на обе части этого уравнения, тогда

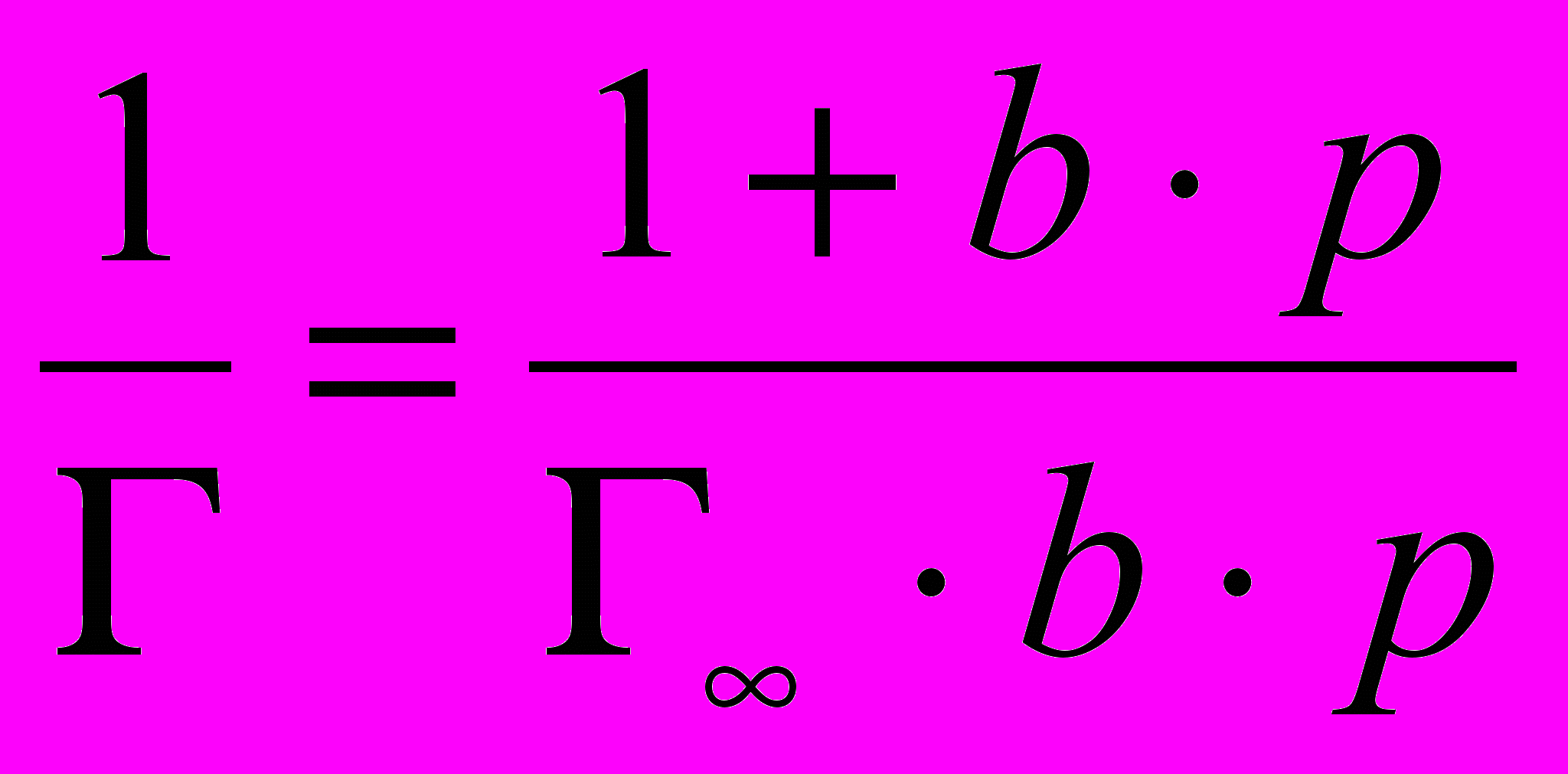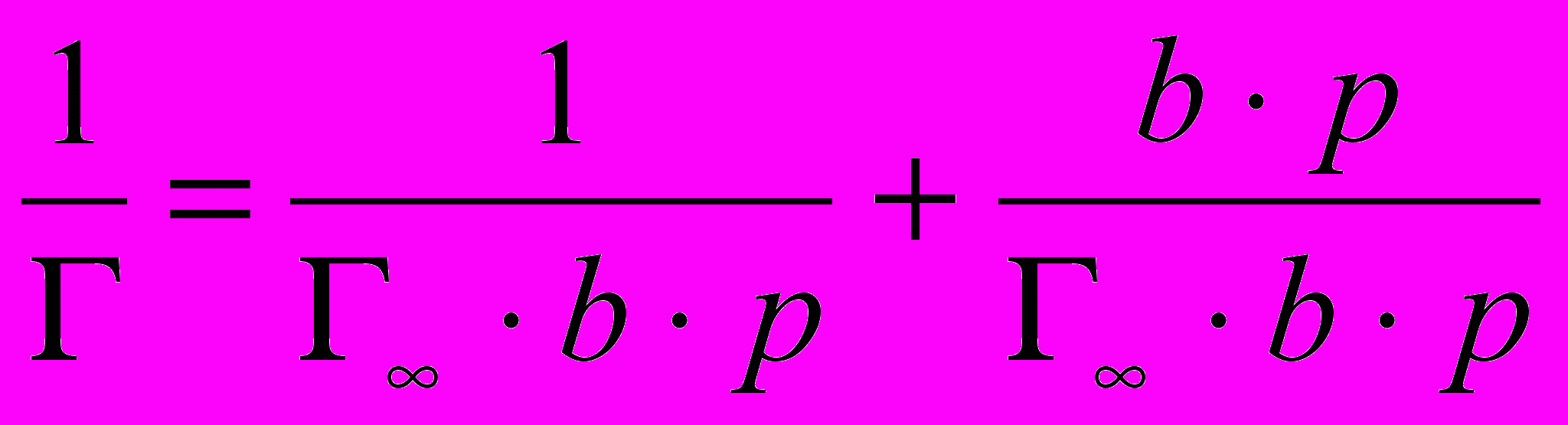; ; при сокращении и преобразовании формулы получается выражение .

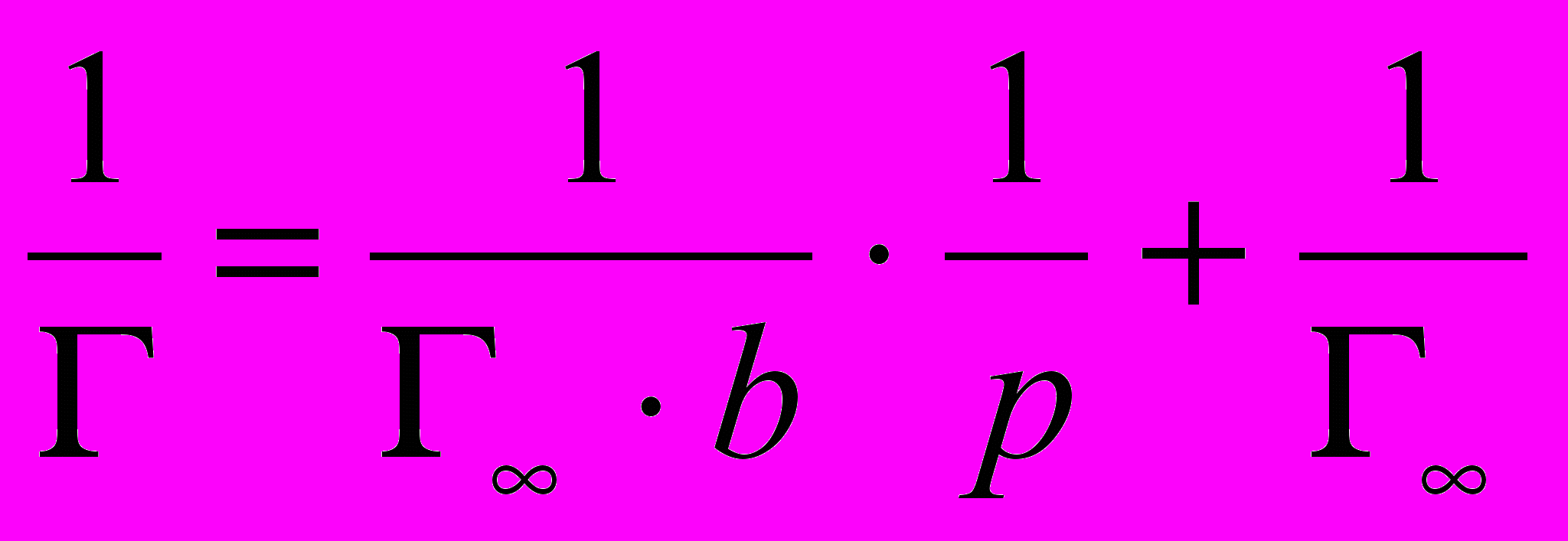Вычисляют значения 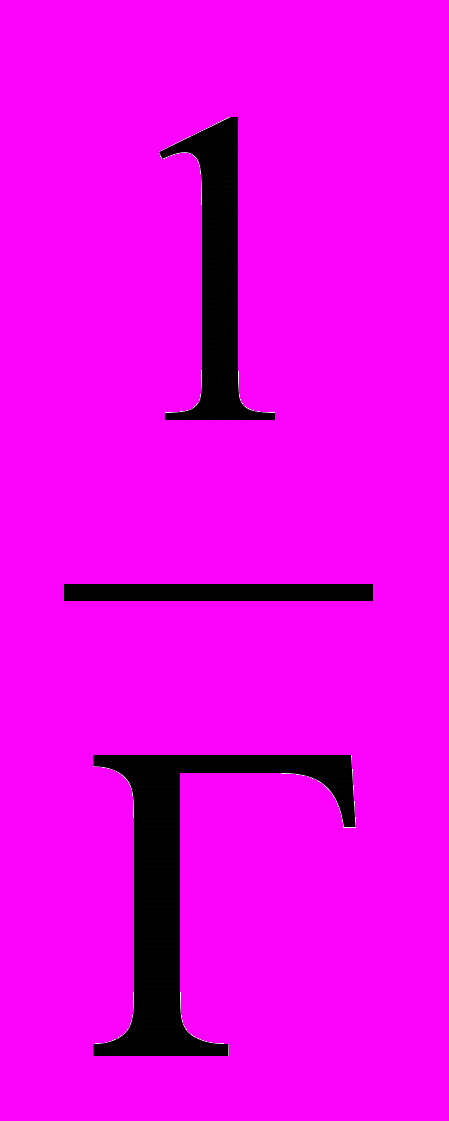и 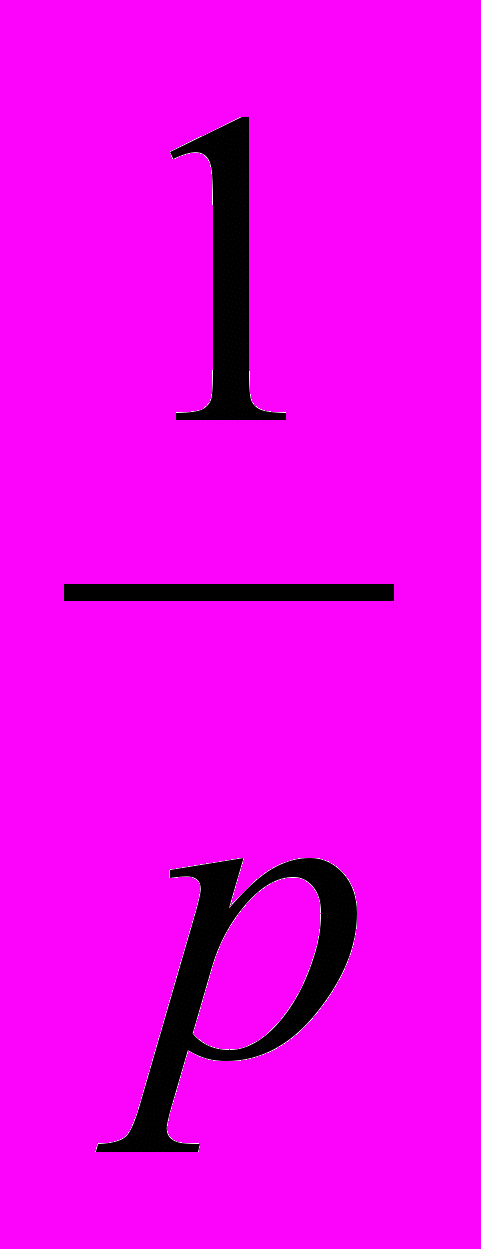и на основании этих расчетов строят график.

1/p·102
1,0
0,2
0,1
0,03
0,013
0,010
0,005

1/Г·10-3
0,029
0,012
0,009
0,007
0,006
0,0056
0,0053

1/Г·10-3

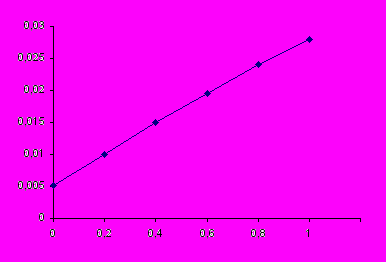1/p·102

Отрезок, отсекаемый прямой на оси ординат равен 1/Г∞ (0,0052·10-3), следовательно Г∞= 192 ·10-3 кмоль/кг. Тангенс угла наклона прямой к оси абсцисс равен 1/(Г∞ ּb).

tgα =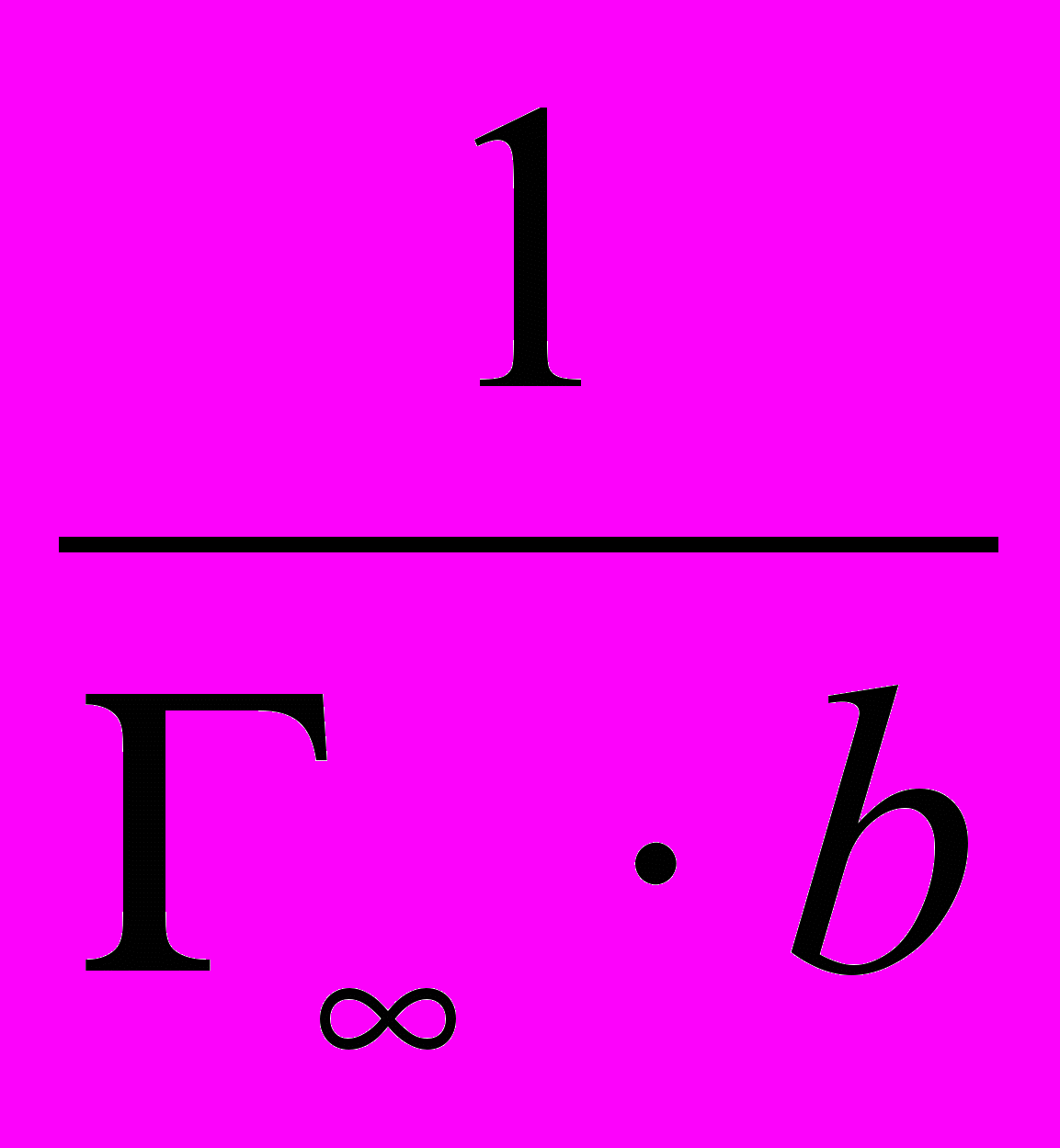; tgα = (0,029-0,0052)·103 / 1,0·10-2 = 2,38·103 (отношение противоположного катета к прилежащему катету по отношению к углу в треугольнике)

b = .


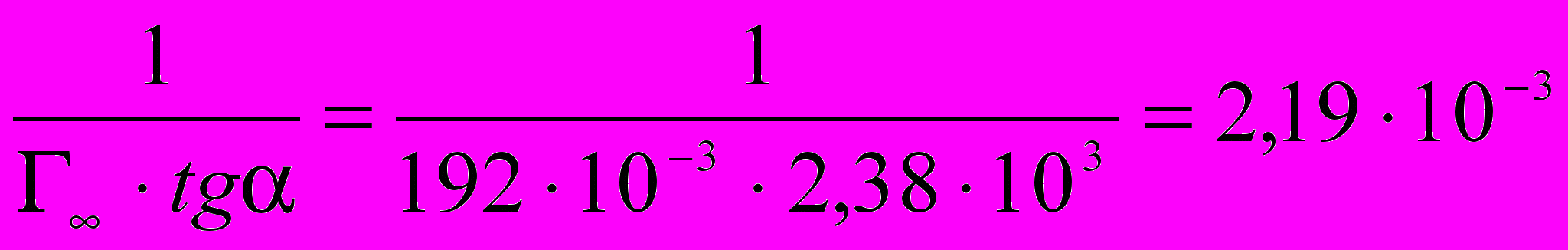Контрольные вопросы

76.Вычислите поверхностное натяжение глицерина, если в капилляре с радиусом r=0.4*10-3м он поднялся на высоту h=26.8*10-3м. Плотность глицерина =1.26кг/м3.

77.Какова величина поверхностного натяжения ртути, если в стеклянном капилляре с радиусом r=0,6*10-3м столбик ее опустился на 12*10-3м ниже уровня ртути в сосуде?

78.Вычислите поверхностное натяжение анилина на границе с воздухом при 292оК, если методом наибольшего давления пузырьков получены следующие результаты: давление пузырьков при проскакивании его в воду равно 11,82*102Н/м2, а анилин- 711,5 Н/м. Поверхностное натяжение воды о=72,55*10-3Н/м.

79. Найдите поверхностное натяжение анилина, если с помощью сталагмометра Траубе получены данные: число капель анилина – 42, плотность его –1,4кг/м 3, число капель воды-18. Температура опыта +2880К. Поверхностное натяжение воды о=73,26*10-3Н/м.

80.Во сколько раз изменится запас свободной поверхностной энергии водяного тумана, если радиус его капелек увеличится от 1*10-6 до 1,2*10-3м при 2880К?

81.Во сколько раз увеличится свободная поверхностная энергия системы при пептизации геля Fe(OH)3, если при этом радиус частиц геля уменьшается от 1*10-6 до 1*10-9м ?

82.Для водного раствора пропилового спирта найдены следующие значения констант уравнения Шишковского (при 2930К): а=14,4*10-3; в=6,6. Вычислите поверхностное натяжение раствора с концентрацией, равной 1кмоль/м3. Поверхностное натяжение воды о=72,53*10-3Н/м.

83.Константы уравнения Шишковского для водного раствора валериановой кислоты при 2730К равны : а=14,72*10-3; в=10,4. При какой концентрации поверхностное натяжение раствора будет составлять 52,1*10-3Н/м, если поверхностное натяжение воды при 2730К равно 75,49*10-3Н/м ?

84.Используя константы уравнения Шишковского (а=12,6*10-3; в=21,5), рассчитайте поверхностное натяжение для водных растворов масляной кислоты при 2730К для следующих концентраций (кмоль/м3) : 0,007; 0,021; 0,05; 0,104 и постройте кривую в координатах  = f ( c ) . Поверхностное натяжение воды о =75,49*10-3Н/м.

85.Пользуясь графическим методом, найти поверхностную активность масляной кислоты на границе водного раствора с воздухом при 2930К по данным :


Концентрация С , кмоль/м3
0,00
0,021
0,050
0,104
0,246

Поверхностное натяжение *10-3 Н/м
72,53
68,12
63,53
58,60
50,30


86.Вычислите адсорбцию масляной кислоты на поверхности раздела водного раствора с воздухом при 2730К и концентрации С=0,1кмоль/м3, если зависимость поверхностного натяжения от концентрации выражается уравнением :

 = 0 -16,7*10-3 ln(1+21,5с).

87.Найдите адсорбцию пропионовой кислоты на поверхности раздела водный раствор-воздух при 2730К и концентрации 0,5кмоль/м3 по константам Шишковского: а=12,5*10-3 и в=7,73.

88.Найдите поверхностную активность валериановой кислоты на границе ее водного раствора с воздухом при 3530К и концентрации 0,01кмоль/м3 по константам Шишковского: а=17,7*10-3 и в=19,72.

89.Вычислите адсорбцию масляной кислоты на поверхности раздела водный раствор-воздух при 2830К и концентрации С=0,104кмоль/м3, используя следующие данные:


Концентрация С , кмоль/м3
0,00
0,021
0,050
0,104
0,246
0,489

Поверхностное натяжение *10-3 Н/м
74,01
69,51
64,30
59,85
51,09
44,00


90.Используя уравнение Ленгмюра, вычислите адсорбцию пропионовой кислоты на поверхности раздела водный раствор-воздух при 2930К и концентрации С=0,1кмоль /м3, если известны константы уравнения Шишковского: а=12,8*10-3; в=7,16.

91.Вычислите по формуле Ленгмюра величину адсорбции изоамилового спирта концентрации С=0,1кмоль /м3 на поверхности раздела водный раствор-воздух при 2920К по данным константам: Г8=8,7*10-9 кмоль/м2 ; в=42.

92.Для водного раствора изомасляной кислоты при 2910К константы Шишковского равны: а=13,1*10-3 и в=2,2. Чему равна адсорбция при концентрациях С1=0,01; С2=0,1; С3=1 кмоль/м3 ?

93.По экспериментальным данным постройте кривую адсорбции паров воды на сорбенте при 353К и с помощью графического метода определить константы уравнения Ленгмюра:

Равновесное давление

Р*10-2, н/м2
1,33
2,66
5,32
6,65
9,30
13,30
17,30

Адсорбция

Г*103, кмоль/кг

7,0
7,7
8,34
8,63
8,90
9,12
9,33



94.Вычислите величину адсорбции азота на цеолите при концентрации 0,1кмоль /м3, если Г8=38,9*10-3 кг/кг, в=0,156*10-2.

95.Найдите площадь, приходящуюся на одну молекулу в насыщенном адсорбционном слое анилина на поверхности его водного раствора, если Г8=6*10-9 кмоль/м2 ?

96.Какова площадь, приходящаяся на одну молекулу изомасляной кислоты на поверхности раздела водный раствор- воздух, если Г8=5,42*10-9 кмоль/м2 ?

97.По константам Лингмюра Г8=182*10-3 и в=0,1*10-2 рассчитайте и постройте кривую адсорбции углекислого газа на активированном угле в пределах следующих равновесных давлений газа: 10*10-2÷400*102 Н/м2.

98.Используя константы эмпирического уравнения Фрейндлиха =1,6*10-3 и =0,48 , постройте кривую адсорбции СО2 на активированном угле при 2710К в интервале давлений от 2*102 до 30*102 Н/м2.

99.Установите, к какому структурному типу сорбентов можно отнести молекулярные сита. Если при сорбции на них паров воды при 353К получены следующие экспериментальные данные :

Равновесное давление

Р*10-2, н/м2
1,33
2,66
5,32
6,65
9,30
13,30
17,30

Адсорбция

Г*103, кмоль/кг
7,0
7,7
8,34
8,63
8,90
9,12
9,33

Давление насыщенного пара рs=472*102 .Н/м2

100.Используя данные задачи 91, определите общую пористость молекулярных сит (молекулярный объем воды V=0.018м3/кмоль при 353К).

101.Определите общую пористость цеолита (адсорбент первого структурного типа) при адсорбции этана при Т=298К, р*10-2=50Н/м2, рs=37*105н/м2, молярный объем этана V=0,064м3/кмоль; Г*103=2,0кмоль/кг.

102.При капиллярной конденсации паров воды в порах активированного угля (293К) получены результаты:


Равновесное давление

Р*10-2, н/м2
5,32
10,0
11,3
12,5
14,7
17,3
20,0
23,3

Величина сорбции

Г*103, кмоль/кг
























по кривой адсорбции
0,5
2,3
4,0
5,0
10,0
16,0
20,0
28,5

по кривой десорбции
0,5
2,5
5,0
7,5
15,0
23,0
27,6
28,5


Покажите наличие гистерезиса и рассчитайте дифференциальную кривую распределения пор по радиусам. Vводы=0,018м3/кмоль, рs=23.4*102Н/м2; воды=72,5*10-3Дж/м2.


103.Постройте кривую капиллярной конденсации (петлю гистерезиса) паров воды и дифференциальную кривую распределения пор активированного угля по радиусам используя данные :


Равновесное давление

Р*10-2, н/м2
4,65
9,3
14,0
18,7
20,9
23,3

Величина сорбции Г*103, кмоль/кг, по кривой адсорбции
0,5
1,5
8,5
20,0
24,0
28,5

по кривой десорбции
0,5
1,5
13,0
27,0
28,0
28,5

Vводы=0,018м3/кмоль, рs=23.4*102Н/м2; воды=72,5*10-3Дж/м2.

104.Построить интегральную и дифференциальную кривые распределения пор по радиусам для активированного угля при капиллярной конденсации паров бензола (2930К):


Равновесное давление

Р*10-2, н/м2
19,8
29,9
39,8
59,6
79,7
89,4

Величина сорбции Г*103, кмоль/кг, по кривой адсорбции
24,0
28,3
31,0
36,0
46,0
55,0

по кривой десорбции
24,0
30,0
37,5
44,0
50,0
55,0

Vбензола=0,089м3/кмоль, рs=99,3*102Н/м2; =28,9*10-3Дж/м2.


105.Построить кривую капиллярной конденсации паров метилового спирта на активированном угле. Используя ветвь десорбции построить интегральную и дифференциальную кривые распределения пор по радиусам (2930К) :


Равновесное давление

Р*10-2, н/м2
12,8
25,6
38,4
51,2
64,0
76,8
90,0
102,0

Величина сорбции

Г*103, кмоль/кг
























по кривой адсорбции
7,5
8,0
8,3
8,6
9,4
10,2
11,4
13,0

по кривой десорбции
7,5
8,3
9,0
9,6
10,2
11,0
11,7
13,0

Vсн3он=0,0406м3/кмоль, рs=128*102Н/м2; =22,6*10-3Дж/м2.


106.Определите, к какому структурному типу сорбентов отнести ионит, если при сорбции на нем паров CCl4 получены данные:


Равновесное давление

Р*10-2, н/м2
30,4
38,8
48,6
77,0
100,5

Величина сорбции

Г*103, кмоль/кг
0,02
0,03
0,04
0,06
0,07

рsccl4=121*102Н/м2.


107.Постройте изотермы адсорбции и десорбции водяного пара на пшеничном глиадине в координатах Г=f (р/рs), по максимальной величине сорбции рассчитайте общую пористость сорбентов, пользуясь данными :


р/рs
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8

Величина сорбции Г*103, кмоль/кг, по кривой адсорбции
1,75
3,22
3,6
4,67
5,55
6,7
6,9
9,18

по кривой десорбции
2,66
3,78
4,9
6,16
6,95
7,7
8,45
9,22

Vводы=0,018м3/кмоль.


108.По данным задачи 99 рассчитайте и постройте интегральную и дифференциальную кривые распределения пор по радиусам. Vводы=0,018м3/кмоль, рs=23.4*102Н/м2; воды=72,5*10-3Дж/м2; R=8,3*103Дж/(град*моль).

109.Как изменится величина общей пористости аэросила (высокодисперсный кремнезем), если до гидротермальной обработки максимальная величина сорбции на нем паров азота составляла 7,5*10-3кмоль/кг, а после обработки 4,0*10-3кмоль/кг ? V паров азота=0,0224м3/кмоль.

110.Пользуясь данными ионного обмена ионов кальция (Г1, С1) и натрия (Г2, С2) на синтетическом катионите, определите графически константу уравнения Никольского К :


С11/2

С2 в растворе
0,2
0,3
0,4
0,5
0,6
0,8

Г11/2

Г2 на сорбенте
0,75
1,0
1,5
1,8
2,4
3,1


111.При изучении реакции обмена Mg- ионов из чернозема с ионами Са из внесенных минеральных удобрений получены данные:



Концентрация ионов в растворе

С*103, кмоль/м3
Количество сорбированных

катионов Г*105кмоль/кг

Mg
Ca
Mg
Ca

2,41
4,75
8,12
42,88

2,25
5,00
7,70
43,30

2,00
5,10
6,90
44,10

1,84
5,50
6,10
44,90

1,53
5,87
4,54
46,46

1,37
5,99
4,12
46,88


Графическим методом определите константу уравнения Никольского К.


112.Определите константу уравнения Никольского К, используя данные реакций обмена ионов Na из раствора натриевой соли на ионы Mg из почвы :


Концентрация ионов в растворе

С*103, кмоль/м3
Количество сорбированных

ионов на почве Г*105кмоль/кг

Na
Mg
Na
Mg

13.8
42.0
1.2
25.4

21.2
38.3
1.9
26.1

38.2
31.9
3.6
27.2

65.0
21.1
8.0
29.3

79.2
14.8
11.7
32.84



ПРИЛОЖЕНИЕ


Таблица 1

Стандартные электродные потенциалы (0)

некоторых металлов (ряд напряжений)



Электрод
0 , В
Электрод
0 , В

Li+/Li
-3.045
Cd2+/Cd
-0.403

Rb+/Rb
-2.925
Co2+/Co
-0.277

K+/K
-2.924
Ni2+/Ni
-0.25

Cs+/Cs
-2.923
Sn2+/Sn
-0.136

Ba2+/Ba
-2.90
Pb2+/Pb
-0.127

Ca2+/Ca
-2.87
Fe3+/Fe
-0.037

Na+/Na
-2.714
2H+/H2
0.000

Mg2+/Mg
-2.37
Sb3+/Sb
+0.20

Al3+/Al
-1.70
Bi3+/Bi
+0.215

Ti2+/Ti
-1.603
Cu2+/Cu
+0.34

Zr4+/Zr
-1.58
Cu+/Cu
+0.52

Mn2+/Mn
-1.18
Hg2+/Hg
+0.79

V2+/V
-1.18
Ag+/Ag
+0.80

Cr2+/Cr
-0.913
Hg2+/Hg
+0.85

Zn2+/Zn
-0.763
Pt2+/Pt
+1.19

Cr3+/Cr
-0.74
Au3+/Au
+1.50

Fe2+/Fe
-0.44
Au+/Au
+1.70



Таблица 2