Пример оценки бизнеса методом сравнения

Вид материала

Подобный материал:

1 2 3 4

(По данным агентства Reuters от 17 сентября 2004 года).

Поскольку в нашем случае известна временная структура процентных ставок:

[r(t₁), r(t₂), …,r(t_k)], 0 < t₁ < t₂ <…< t_k,

то можно определить безрисковые процентные ставки r(t) по инвестициям в Еврооблигации на любой срок t, t О[0, t_k]. Кроме того, если имеются Еврооблигации со сроком погашения больше r(t_k), то можно определить и безрисковые процентные ставки r(t) при t > t_k.

Таким образом, при известной временной структуре процентных ставок

[r(t₁), r(t₂), …,r(t_k)], где 0 < t₁ < t₂ <…< t_k

Построим кривую рыночных доходностей на отрезке [0, t_k].

Для этого воспользуемся процедурой интерполирования и применим полином Лагранжа r_k(t) степени, не большей, чем k, который проходит через k +1 точку (t₀, r₀), (t₁, r₁), …, (t_k, r_k) и имеет вид

где L_K,i – коэффициенты полинома Лагранжа, основанного на этих узлах:

При этом, члены (t – t_i) и (t_i – t_i) не появляются в правой части выражения в формуле для коэффициентов полинома Лагранжа.

Тогда подставляя значения доходностей к погашению (YTM) и сроки, оставшиеся до погашения (t) для Еврооблигаций из таблицы №7, при t =2 в формулу для полинома Лагранжа получим r = 4,164%.

Воспользуемся теперь методом наименьших квадратов и построим уравнение регрессии, показывающее зависимость текущей доходности Еврооблигаций до погашения от срока (r, YTM), оставшегося до погашения (t).

(Рис. № 3)

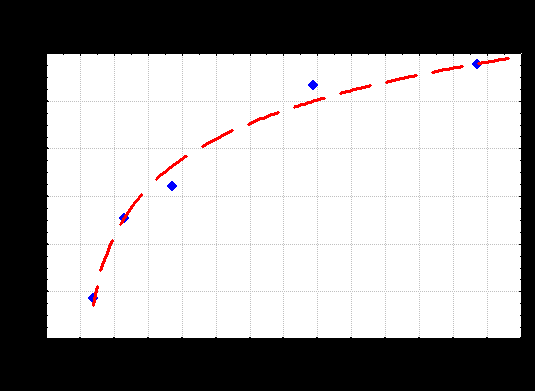
Полученная зависимость имеет вид логарифмической функции:

r = 3,1473 + 3,3876*lg(T)

Следовательно, на основе полученной зависимости (r= 3,1473 + 3,3876*lg(T)) можно утверждать с вероятностью 92,3% (коэффициент парной корреляции Б=0,923), что существует временная зависимость (termstructure) между доходностью к погашению (YTM) и сроком к погашению Еврооблигаций. Существует причинно-следственная связь между ожидаемыми спот-ставками, и видом временной зависимости. В нашем случае зависимость имеет вид возрастающей кривой. Полученный вид кривой объясняется двумя теориями:

q Теорией непредвзятых ожиданий (ожидаемая будущая спот-ставка равна по величине соответствующей форвардной ставке, то есть ожидаемое увеличение годовой спот-ставки является причиной возрастания кривой доходности).

q Теории наилучшей ликвидности (ожидаемая спот-ставка должна быть несколько меньше, чем форвардная ставка на величину премии за ликвидность).

Однако премия за ликвидность для ценных бумаг со сроком погашения более одного года не превышают премии за ликвидность ценных бумаг со сроком погашения до одного года (L_0,5;1 = L _1;1,5).

Таким образом, принимая во внимание теорию непредвзятых ожиданий, Оценщики в своих расчётах руководствуются, что премия за ликвидность для спот-ставок, со сроком погашения более чем один год не меняется.

Следовательно, подставляя значение срока до погашения в полученную регрессионную зависимость для Еврооблигаций YTM = 3,1473 + 3,3876*lg(T) при Т = 2,0 года, получим валютную доходность для Еврооблигаций с данным сроком погашения равную 4,17 %.

Таблица значения полученной доходности Еврооблигаций МинФина РФ со сроком погашения два года.

(Таблица №8)

Эмитент	Валюта	Срок до погашения на момент оценки, t, лет.	Доходность, r, YTM, % год на основе интеполяционного полинома Лагранжа.	Доходность, r, YTM, % год на основе метода наименьших кадратов.
Еврооблигации, Минфин РФ	доллары США	2	4,164	4,17

Коэффициент странового риска РФ по отношению к США равняется:

К _США_/_РФ =

где:

YTM_США_/2 –    доходность Гособлигаций США, со сроком погашения через 24 месяца;

YTM_РФ_/2 –      доходность Еврооблигаций Минфина РФ, со сроком погашения через 24 месяца;

Коэффициент странового риска РФ по отношению к Бразилии равняется:

К _{Бразилия}_/_РФ =

где:

YTM _Brazil-07 – доходность Еврооблигаций Бразилии, со сроком погашения 26.июня 2007 года;

YTM _Russia-07 – доходность Еврооблигаций Минфина Российской Федерации, со сроком погашения 26.июня 2007 года.

(По данным агентства Reuters от 17 сентября 2004 года).

4.5.      Расчёт поправки, учитывающий весовые коэффициенты для компаний-аналогов.

К расчёту весовых коэффициентов для отобранных компаний аналогов оценщики подошли с позиции построения оптимального портфеля. Согласно теореме об эффективном множестве (efficient set theorem) инвестор выбирает оптимальный портфель из множества портфелей, каждый из которых:

 обеспечивает максимальную ожидаемую доходность для некоторого уровня риска.

 обеспечивает минимальный риск для некоторого значения ожидаемой доходности.

Таким образом, набор портфелей, удовлетворяющий этим двум условиям, называется эффективным множеством, или эффективной границей.

График выбора (построения) оптимального портфеля при заданном уровне доходности.

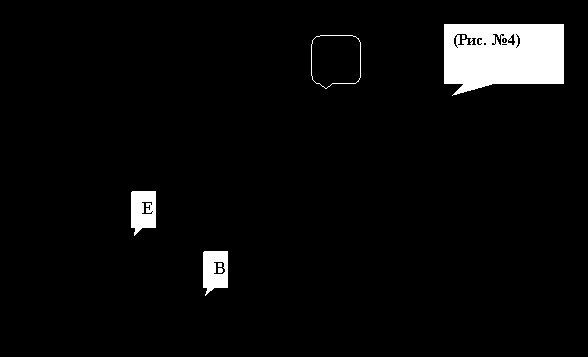
Кривые безразличия инвестора, не расположенного к риску, который принимает свои решения на основе математического ожидания и дисперсии, всегда имеют форму вогнутых кривых с положительным углом наклона. Очевидно, что все портфели, находящиеся на непрерывно начерченной части кривой EGA, превосходят те, которые расположены на пунктирно начерченной кривой ЕВ, то есть множество портфелей, обеспечивающих минимальный риск при изменяющемся уровне ожидаемой доходности, является часть левой границы достижимого множества, расположенная между точками EGA. Соответственно эти портфели составляют эффективное множество, и из этого множества эффективных портфелей (efficient portfolios) Оценщики будут выбирать оптимальный для себя портфель.

Все остальные достижимые портфели являются неэффективными портфелями (inefficient portfolios), поэтому Оценщики вправе их игнорировать.

Следовательно, оптимальный портфель с заданным значением доходности можно найти с помощью кривой безразличия, которая касается кривой эффективных портфелей. На рисунке № 4 это такое касание происходит в точке G.

При этом Оценщики отмечают, что согласно двум предположениям о ненасыщаемости (nonsatiation), то есть предполагается, что инвестор предпочитает более высокий уровень конечного благосостояния более низкому его уровню, и об избегании риска является причиной выпуклости и положительного наклона кривой безразличия.

4.5.1. Расчёт доходности, формируемого портфеля, состоящего из компаний аналогов.

При формировании оптимального портфеля, задаётся определённый уровень доходности, который обеспечивает минимальный риск (точка G, рис.№4). При этом Оценщики полагают, что задаваемый уровень доходности формируемого оптимального портфеля должен отражать средний уровень производственного и финансового рисков оцениваемой компании, и уровень альтернативных вложений, в качестве которого выступает значение средневзвешенной стоимости капитала (WACC). Следует отметить, что WACC отражает предельные затраты источников формирования капитала при формировании инвестиционного бюджета.

Расчёт стоимости акционерного капитала Оценщики проводят на основе модели САРМ.

Согласно теории САРМ, разработанной У. Шарпом, рыночный риск любой акции (актива) может быть оценён на основе анализа тенденции изменения её характеристик по отношению к среднерыночным их значениям.

Наиболее важная черта этой модели заключается в том, что ожидаемая доходность акции (актива) увязывается со степенью рискованности этого актива, измеряемой коэффициентом, называемым "бета" (b).

В модели САРМ (Capital Asset Pricing Model) простым образом определяется связь между риском и доходностью эффективных портфелей. Точка касания прямой к кривой портфелей эффективного множества обычно обозначается точкой М, которая определяет рыночный портфель (портфель, состоящий из всех ценных бумаг, в котором доля каждой соответствует её относительной рыночной стоимости), а r_f представляет собой безрисковую ставку доходности.

 График рыночной линии ценной бумаги (актива)

Эффективные портфели находятся вдоль прямой, пересекающей ось ординат в точке с координатами (0, r) и проходящей через М, и образуется альтернативными комбинациями риска и доходности, получаемыми в результате сочетания рыночного портфеля с безрисковым заимствованием или кредитованием. Это линейное эффективное множество в САМР известно под названием рыночная линия (Capital Market Line, CML).

Все остальные портфели, не использующие рыночный портфель в комбинации с безрисковым заимствованием или кредитованием, будут лежать ниже рыночной прямой.

Наклон CML равен разнице между ожидаемой доходностью рыночного портфеля и безрисковой бумаги ( r_M– r_f), делённой на разницу их рисков (s_М – 0).

r_S _САРМ= r_f + ( r_M – r_f )*b_.

где:

r_САРМ – доходность произвольно выбранного актива или портфеля акций на основе модели САРМ.

r_f - безрисковая ставка доходности.

r_M – среднерыночная доходность.

s²_М – дисперсия рыночного портфеля.

b = - «бета»-коэффициент систематического рыночного риска, характеризующий изменчивость доходности акций оцениваемого предприятия относительно доходности всего рынка в целом (фондового индекса).

Таким образом, модель CAMP предполагает, что премия за систематический риск активов (ценных бумаг) оцениваемой отрасли пропорциональна премии за риск по рыночному портфелю (фондовому индексу) с коэффициентом пропорциональности b:

( r_M– r_f)x b

4.5.2. Обоснование безрисковой ставки для американского фондового рынка.

Оценщики считают правомерным в качестве текущей безрисковой ставки для принять текущую доходность к погашению (Yield to maturity) Гособлигаций США со сроком через два года (наиболее прогнозируемый срок, обычно принимаемый в расчётах при оценке среднерыночной доходности).

Валютная текущая доходность к погашению (Yield to maturity) Гособлигации США (погашение 31.августа 2006 года) составляет на 17.сентября 2004 года r_fСША = 2,478 % годовых.

(По данным агентства Reuteres от 17.сентября 2004 года)

4.5.3. Обоснование среднерыночной доходности американского фондового рынка.

Для расчёта среднерыночной доходности американского фондового рынка обычно применяют индекс S&P-500, который включает акции 500 ведущих американских промышленных компаний.

r_S&P-500 = S&P-500_i+1 / S&P-500_i – 1.

где:

S&P-500_i+1 – значение индекса в период i+1.

S&P-500_i– значение индекса в период i.

Таблица значений индекса S&P-500 и его доходности за период октябрь 2002 – октябрь 2004 годов.

(Таблица №9)

№ п/п	Среднемесячное значение индекса S&P–500	Период	Доходность индекса S&P-500, %.
1.	885,77	Октябрь 2002 года
2.	1050,7	Октябрь 2003 года	18,6
3.	1131,5	Октябрь 2004 года	7,7

Среднегеометрическое значение доходности индекса S&P–500 за два последние года составило: r_M = –1=

Таким образом, значение среднерыночной текущей доходности американского фондового рынка на основе динамики индекса S&P–500 за период с октября 2002 по октябрь 2004 года составило r_M =13%.

4.5.4.   Расчёт премии за риск инвестирования в корпоративные активы металлургической отрасли РФ.

Формула для расчёта среднерыночной премии за риск для Российских металлургических предприятий, на основе данных американского фондового рынка имеет ниже следующий вид:

. _premium= [( r_MСША – r_fСША)*b] / К _США_/_РФ.

Где:b= 1,33 - коэффициент, характеризующий изменчивость доходности акций предприятий американской металлургической отрасли, относительно доходности рынка ценных бумаг на американском фондовом рынке, в данном случае относительно фондового индекса S&P–500 по состоянию на октябрь 2004 года, то есть в данном случае были идентифицированы металлургические компании, котирующиеся в NYSE. Таким образом, при расчёте значения b использовался так называемый метод чистой игры (pure play method). При этом участие заёмных средств в финансировании деятельности компаний, то есть структура капитала, уже отражено в установленном рынком значении b= 1,33. b собственного капитал фирмы является функцией как производственного риска активов компании, показателем которого является b_U, так и способа финансирования активов. Тем не менее, представляет интерес среднее внутренне значение b текущих активов, то есть то значение b, которое компания имела бы, если бы не привлекала заёмные средства. Для этого устраним влияние структуры источников финансирования.

T _USA = 0,34 – предельное значение ставки налога на прибыль в США.

D/E (LT Debt to Equity (MRQ)) = 0,72 – среднее значение доли долгосрочной задолженности в активах для металлургических американских компаний, котирующихся в NYSE по материалам агентства Reuters.

Таким образом, b функционирующих активов американских металлургических компаний, котирующихся в NYSE, под которыми понимаются главным образом основные производственные фонды, используемые для производства выпускаемой продукции (металла), равняется 0,902.

Обращаясь к базе данных Системы Комплексного Раскрытия Информации (СКРИН) авторы статьи пришли к заключению, что доля долгосрочной задолженности в совокупных активах Российских компаний на конец 2003 года, занимающихся производством стали классическим способом (из руды и коксующегося угля), большинство которых относится к категории С+, находится в интервале от 5 до 19%. Тогда значение b для компаний доля долгосрочной задолженности которой в общем объёме активов (D/E), в среднем, составляет 20% равняется:

= 0,902 x [1+(1– 0,24)x 0,2] = 1,04.

где: T _RUSSIA = 0,24 – предельная ставка налога на прибыль в РФ.

. _premium= [( r_MСША – r_fСША)*b] / К _США_/_РФ = [(13 – 2,478)*1,04] / 0,594 = 18,42%.

Следовательно, среднерыночное значение премии за риск для Российских металлургических предприятий, на основе данных американского фондового рынка, равняется 18,42 % годовых.

4.5.5.   Расчет значения доходности формируемого оптимального портфеля, включающего компании аналоги на основе значения WACC оцениваемой компании.

Используя модель САМР с поправкой на коэффициент странового риска, получаем значение стоимости собственного капитала для оцениваемой Российской металлургической компании:

r_SСАМР= [r_fСША + (r_MСША – r_fСША)*b_L] / К _США_/_РФ =

[2,478 + (13 – 2,478)*1,04] / 0,594 = 22,6%.

Придерживаясь допущения, что доля долгосрочной задолженности в совокупном объёме активов составляет 20%, а средний процент по валютным долгосрочным кредитам (1-3 года) на кредитном рынке РФ в 2004 году составляет 12% годовых.

WACC = w_d k_d (1–T_RUSSIA) + w_s k_S_CAMP

где:

w_d= 0,20 – доля долгосрочной задолженности (долгосрочные кредиты) в общем объёме активов компании.

k_d = 12% – средний процент по валютным долгосрочным кредитам сроком на 1 – 3 года на кредитном рынке РФ в 2004 году.

T_RUSSIA= 0,24 – предельная величина ставки налога на прибыль в РФ.

K_SCAMP = 22,6% – стоимость собственного капитала для оцениваемой Российской металлургической компании.

w_s = 0,80 – доля собственного капитала в общем объёме активов компании.

WACC = 0,20 x 12 x (1 – 0,24) + 0,80 x22,6 = 19,9%

Таким образом, значение доходности формируемого оптимального портфеля, состоящего из американских металлургических компаний, рассчитанное на основе значения средневзвешенной стоимости капитала (WACC), равняется 20%.

4.5.6.   Расчет весовых коэффициентов () для мультипликаторов компаний аналогов при построении оптимального портфеля.

Постановка задачи. Предположим, что на рынке имеются ценные бумаги n (в нашем случае n равняется количеству компаний аналогов) видов с ожидаемыми доходностями , , , …, , ковариационная матрица доходностей которых имеет следующий вид:

                         (4.1)

Будем считать, что ранг матрицы › равен количеству видов ценных бумаг, то есть r (›) = n, а среди чисел , , , …, есть несовпадающие.

Множество недоминируемых портфелей, называемое эффективной границей, может быть построено решением общей задачи минимизации риска (задача выпуклого программирования), впервые рассмотренной Г. Марковицем:

                                           (4.2)

При трёх дополнительных ограничениях (4.3):

1.     – данное ограничение фиксирует желаемый уровень доходности (значение среднерыночной доходности оцениваемой отрасли) создаваемого портфеля.

2.     – ограничение нормирует весовые коэффициенты портфеля, то есть формируется множество ценных бумаг (активов), с помощью которых инвестор формирует свой портфель.

3.     – третье ограничение разрешает покупку ценных бумаг только с покрытием, то есть накладывается ограничение на продажу ценных бумаг (активов) без покрытия («короткая продажа»).

Целевая функция Лагранжа для задачи минимизации риска при фиксированном уровне доходности записывается следующим образом:

(4.4)

Для определения процентных долей, которые минимизируют риск, необходимо приравнять производные функции Лагранжа по _j (j =1, …n), по »₁ и по l₂ и _ к нулю (поиск точек, удовлетворяющих условиям Кюна-Такера).

Таким образом, возникает система (n+3) линейных уравнений с (n+3) неизвестными, которая, как правило, имеет однозначное решение.

В матричной форме записи система имеет следующую структуру:

                   (4.5)

__i_i= 0, __i e 0, _i e 0, i =1,2 …, n.                                                          (4.6)

- значение доходности i-ой ценной бумаги (актива) за рассматриваемой период времени, а P_iиP _i+1 – рыночные цены акций (активов) в период i и i +1.       (4.7)

E( r_i) _.=- среднее значение доходности i-ой акции (актива) за n периодов.   (4.8)

- значение ковариации между i-ой и j-ой ценными бумагами.                                                                                                                       (4.9)

E( r_i _год) = E( r_i _мес.) x 12– годовое значение доходности i-ой акции.                     (4.10)

Г _ij _год. = Г _ijмес x 12 – годовое значение доходности ковариации между i-ой и j-ой ценными бумагами.                                                   (4.11)

Так как r (›) = n, а среди чисел , , , …, имеются несовпадающие, к системе линейных уравнений можно применить метод Гаусса (последовательного исключения), который можно описать ниже следующим образом:

Пусть дана система

, в матричном виде АХ=В

                    (4.12)

Если , а также ведущие элементы i = 2, 3, …, n, остальных строк, получаемые в процессе вычислений, отличны от нуля, то выше отмеченная система приводится к треугольному виду:

                                                                    (4.13)

и может быть записана в матричном виде U X = Y , где U - верхняя треугольная матрица. После построения матриц U и Y можно использовать обратную подстановку, чтобы решить систему UX=Y для Y.

                   (4.14)

Ведущие элементы и коэффициенты системы находятся с помощью ниже следующих формул

,                                 (4.15)

где: k+1_ j _ n+1, k+1 _ i _ n+1, k =1,2…,n.

Обратный ход можно совершить иначе, если обратить в нуль и все коэффициенты, лежащие выше главной диагонали. Например, элементы k-го столбца обращаются в нуль, если умножить на и сложить с соответствующей строкой. Аналогично обращаются в нуль и все остальные столбцы. Если, кроме того, разделить затем каждое уравнение на соответствующий элемент, стоящий на главной диагонали, то матрица системы становится единичной.

Таким образом, после ряда последовательных преобразований методом последовательных исключений (метод Гаусса) получаем систему в виде таблицы №10.

Таблица системы уравнений (4.6) (матричная форма) после преобразования по методу Гаусса в общем виде.

(Таблица №10)

₁	₂	…	_n	₁	₂	_₁	_₂	…	__n
1	0	…	0	0	0	C₁₁	C₁₂	…	C_1n
0	1	…	0	0	0	C₂₁	C₂₂	…	C_2n
…	…	…	…	….	…	…	…	…	…
0	0	…	1	0	0	C_n1	C_n2	…	C_nn
0	0	…	0	1	0	C_n+1,1	C_n+1,2	…	C_n+1,n
0	0	….	0	0	1	C_n+2,1	C_n+2,n	…	C_n+2,n

Поскольку на неизвестные ₁ и ₂ нет никаких ограничений, можно вычеркнуть два столбца, соответствующие этим значениям, и последние две строи. Получим систему линейных уравнений, записанную в ниже следующей таблице:

(Таблица №11)

₁	₂	…	_n	_₁	_₂	…	__n
1	0	…	0	C₁₁	C₁₂	…	C_1n
0	1	…	0	C₂₁	C₂₂	…	C_2n
…	…	…	…	…	…	…	…
0	0	…	1	C_n1	C_n2	…	C_nn

Blog

Пример оценки бизнеса методом сравнения