Методика определения корректировок на различия в численных значениях элементов сравнения на основе функции полезности

Вид материала

Документы

Содержание Unit of an Element of Comparison Относительная корректировка S = 1. Рассмотрим подробнее, что представляют собой функции полезности единицы элемента сравнения u(x Список использованной литературы

Подобный материал:

• Программа вступительного экзамена в магистратуру по экономической теории Утверждена, 119.73kb.
• Исследование изменения свойств материалов при блистринге методом стохастического моделирования, 19.3kb.
• Лекция 11. Индивидуальный и рыночный спрос, 58.12kb.
• Методика определения пористости форм Методика определения эффективного диаметра пор, 240.07kb.
• Различия в одаренности могут быть связаны как с мерой проявления признаков одаренности,, 84.75kb.
• Применение ионометрического метода определения йодид-ионов для мониторинга йоддефицитных, 31.31kb.
• Ым, во-первых потому что общего (единого) алгоритма их вычисления нет, а во-вторых, 15.16kb.
• Программа дисциплины «Математический анализ», 500.52kb.
• Программа дисциплины «математический анализ», 432.47kb.
• Методика определения стойкости криптосистем 20 Криптопротоколы, их классификация, особенности, 972.89kb.

Методика определения корректировок на различия в численных значениях элементов сравнения на основе функции полезности


Автор: ссылка скрыта

E-mail: SSkorkin@rambler.ru


Процедура сравнения лежит в самой основе оценочной деятельности. В своей практике оценщику постоянно приходиться производить сопоставление и сравнение исследуемого объекта (объекта оценки) с другими объектами, аналогичными ему по своим основным характеристикам.

Основной же проблемой при определении величины стоимости объекта оценки путем его сравнения с аналогичными объектами является то обстоятельство, что двух объектов с полностью идентичными характеристиками не существует. Отсюда вытекает необходимость корректировки цен объектов-аналогов с учетом данных различий.

Таким образом, точность и обоснованность корректировок является краеугольным камнем любого исследования, направленного на определение стоимости.

В оценочной практике существует ряд методик определения размера корректировок на различия в характеристиках сравниваемых объектов. Из них можно выделить две основные группы [1]:

• Методы, основанные на количественном анализе рынка объектов, аналогичных объекту оценки. К данной группе можно отнести: метод анализа парных продаж, метод корреляционно-регрессионного анализа, метод анализа издержек, метод попарного сопоставления дохода двух аналогов и т.д.;
  
• Экспертные методы, основанные на суждениях оценщика или других экспертов. К этим методам можно отнести методы анкетного опроса, интервью и методы "Дельфи" и т.д.;
  

Обе данные группы методов обладают как своими преимуществами, так и недостатками. Так основными недостатками методов, основанных на количественном анализе рыночной среды, является частое отсутствие, неполнота или недоступность информации, необходимой для вычисления корректировок, а также высокая трудозатратность данных методов. Экспертные методы, в свою очередь, основываются на субъективном мнении (мнениях) и в достаточной мере зависят от опыта и личности эксперта. Главным их недостатком является высокая степень субъективности получаемых оценок.

В данной статье автором предлагается методика определения величины корректировок, сочетающая, по мнению автора, объективность и обоснованность методов количественного анализа с оперативностью экспертных методов.

Последовательность сравнения объекта оценки с объектами-аналогами обычно выглядит следующим образом: оценщик выбирает единицу сравнения, которая в последствии корректируется при помощи коэффициентов либо при помощи относительных (или абсолютных) корректировок с учетом степени различия в характеристиках элементов сравнения объекта оценки с объектом-аналогом.

Корректировочный коэффициент для единицы элемента сравнения ( Unit of an Element of Comparison) сопоставимого объекта определяется как отношение полезности единицы блага элемента сравнения объекта оценки к полезности единицы блага элемента сравнения объекта-аналога:



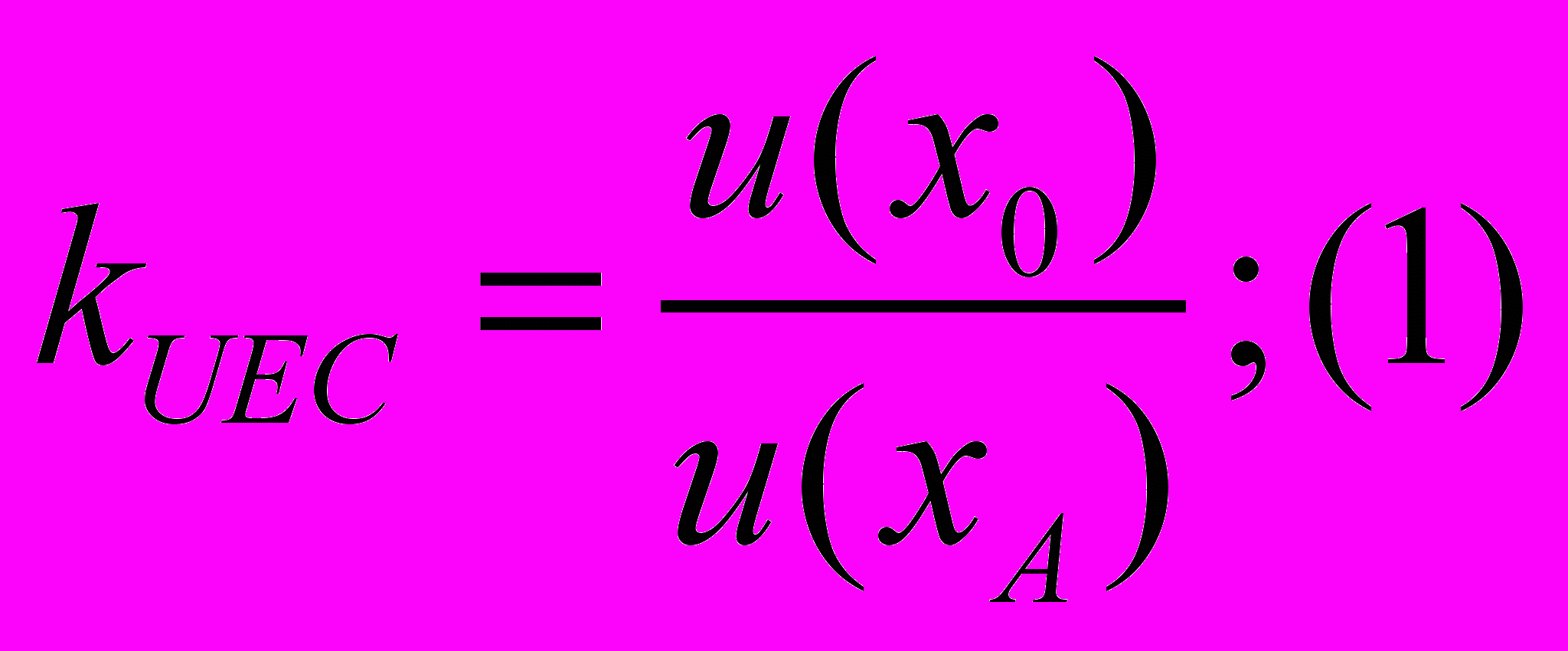
Где u(x₀) – полезность единицы блага элемента сравнения объекта оценки;

u(x_A) – полезность единицы блага элемента сравнения объекта-аналога;

x₀ – количество единиц блага элемента сравнения объекта оценки;

x_A – количество единиц блага элемента сравнения объекта-аналога;

(x₀ > 0, x_A > 0 (по определению блага, как объекта, имеющего положительную общественную полезность [3]))

Относительная корректировка для единицы элемента сравнения сопоставимого объекта – по формуле:




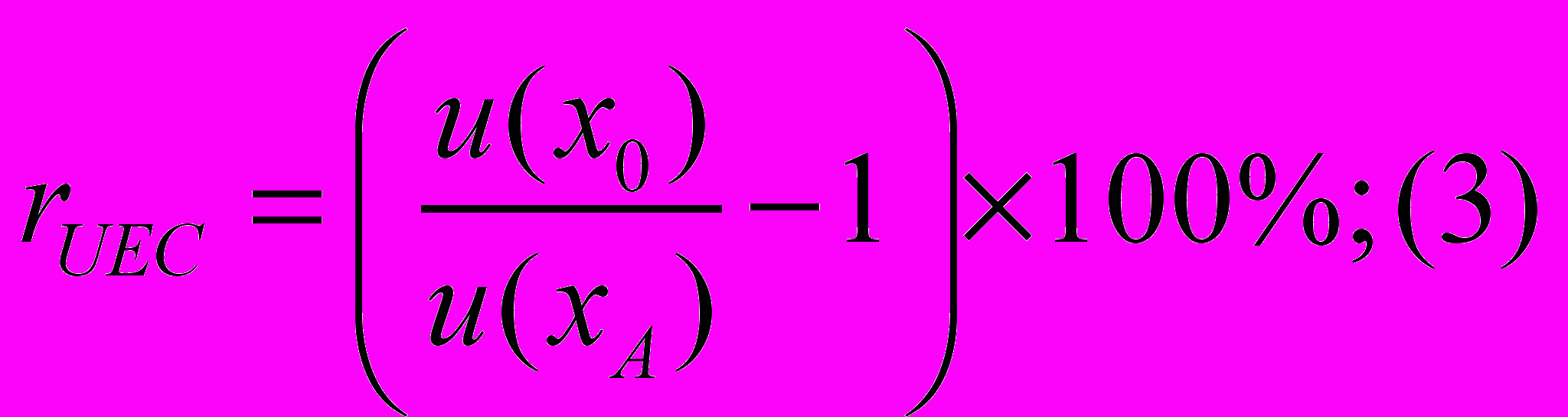
Данные формулы показывают во сколько раз (на сколько процентов) единица элемента сравнения, анализируемого элемента, полезнее единицы элемента сравнения сопоставимого объекта-аналога.

Для получения значения итоговой корректировки на различия в значениях элементов сравнения необходимо учесть величину доли элемента сравнения в общей стоимости объекта оценки ():







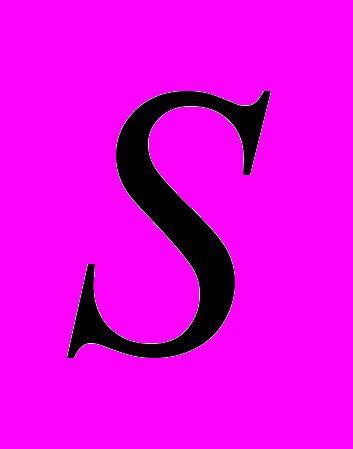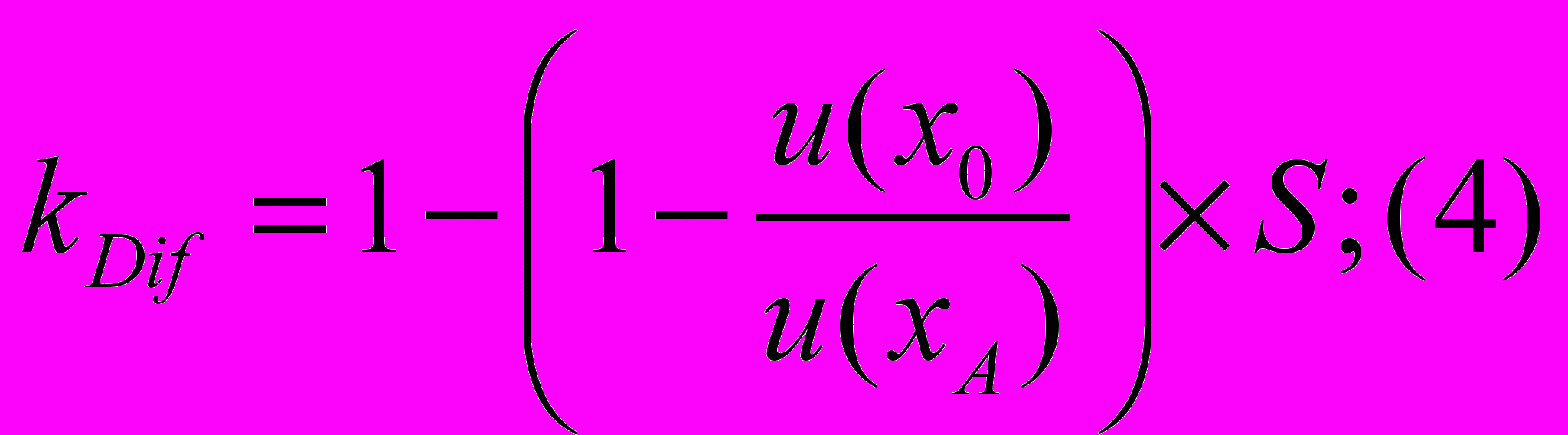
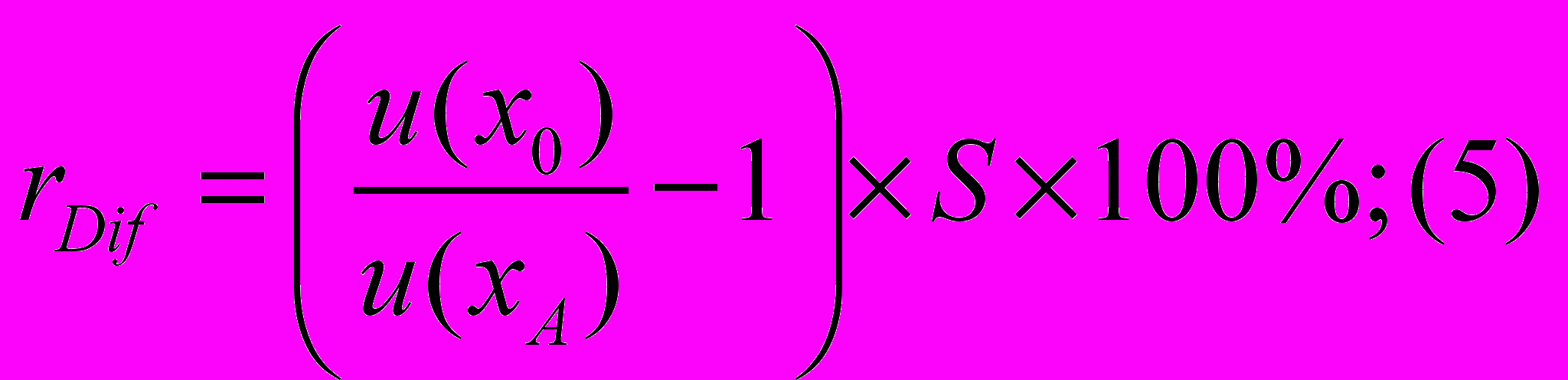
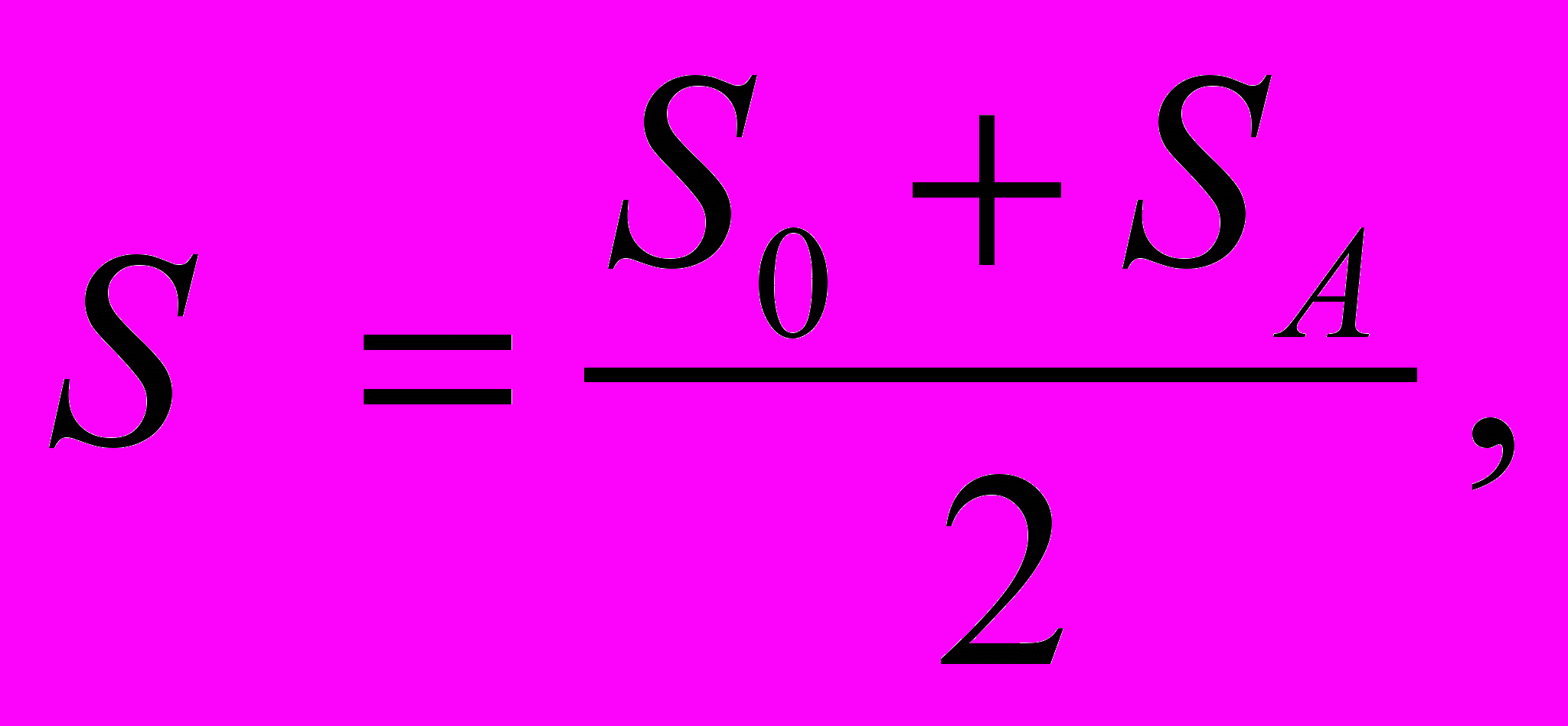
S₀ – доля элемента сравнения объекта оценки в его общей стоимости;

S_A – доля элемента сравнения объекта-аналога в его общей стоимости;

При этом в случае, если элементом сравнения является целый объект (здание, земельный участок и т.д.) S = 1.

Рассмотрим подробнее, что представляют собой функции полезности единицы элемента сравнения u(x₀), u(x_A).

В экономических исследованиях, как правило, используются некоторые конкретные виды выпуклых функций полезности, причем подбор вида функции и оценка числовых значений параметров производятся на основе наблюдений и анализа поведения потребителей [4].

Одной из основных функций полезности, характеризующих финансовое поведение людей, является функция u(x) ~ ln x (рисунок 1). Это следует со следующих рассуждений: полезность бесконечно малого выигрыша dx пропорциональна этому выигрышу и обратно пропорциональна денежной сумме, которой игрок обладает [4]:

du = u(x + dx) - u(x), (6)

Следовательно:

u(x) ~ ln(x) или u(x) = a ln(x) + b, (7)



Рис. 1. График зависимости полезности элемента сравнения от количества единиц сравнения

Тогда зависимость полезности одной единицы блага рассматриваемого элемента сравнения от количества блага (размера, объема) данного элемента сравнения выражается следующей формулой:



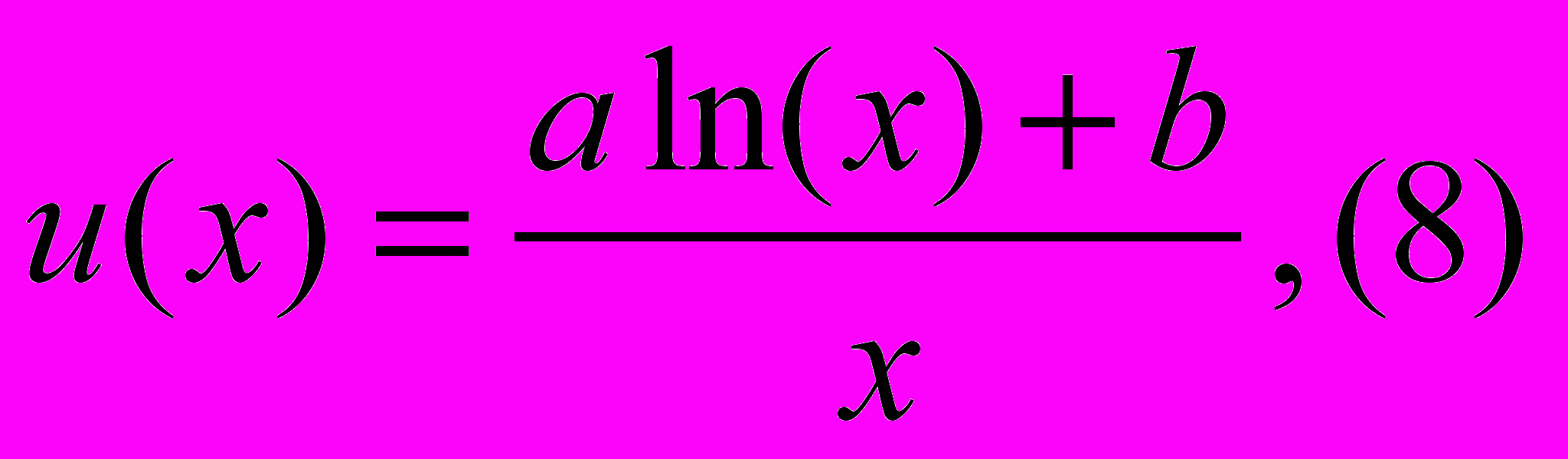
(x >0), а формулы (4) и (5) приобретают вид:







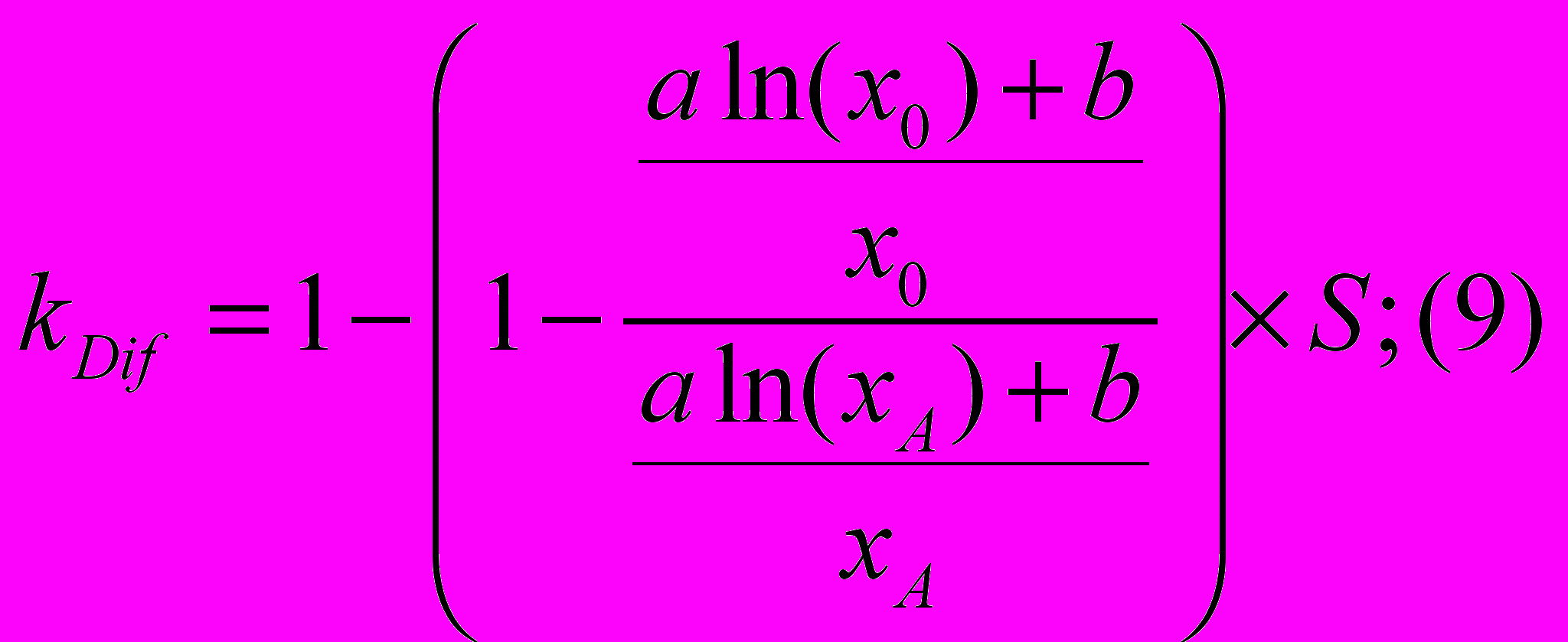
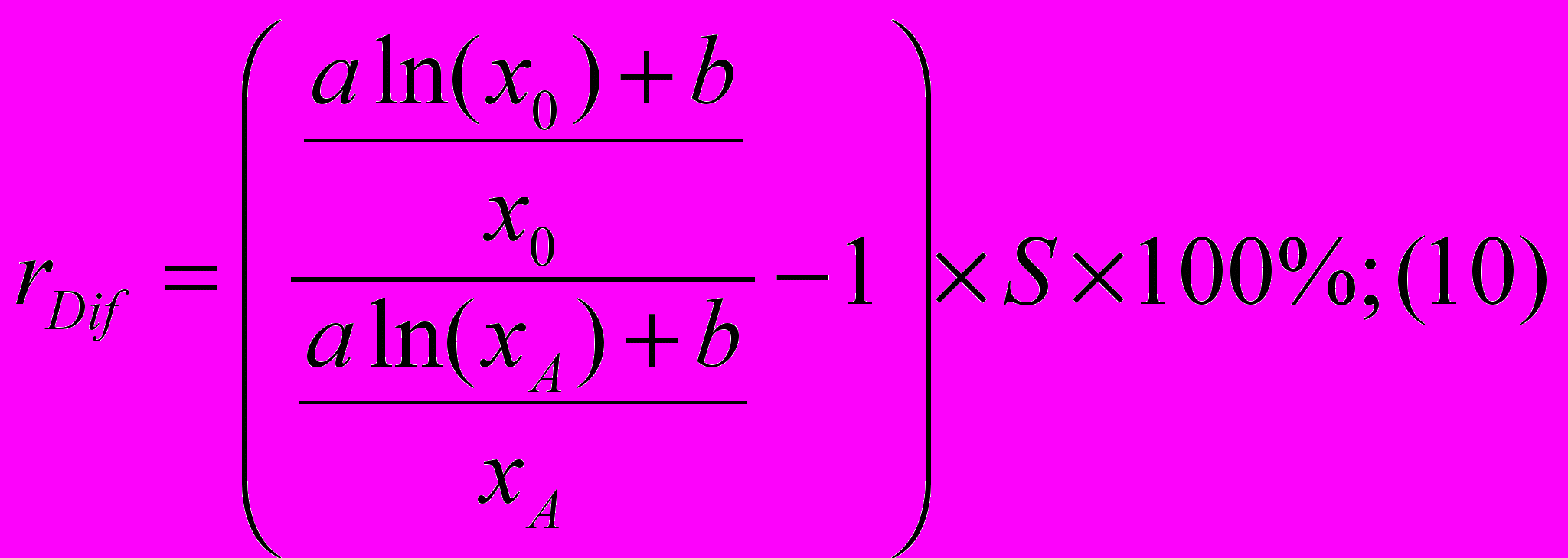
В соответствии с первым законом Госсена [2] (законом убывающей полезности) величина удовлетворения u от потребления каждой дополнительной единицы блага x данного вида уменьшается, пока не достигнет нуля в точке полного насыщения. Иными словами, существует такое x, при котором Df(u) = 0 или:




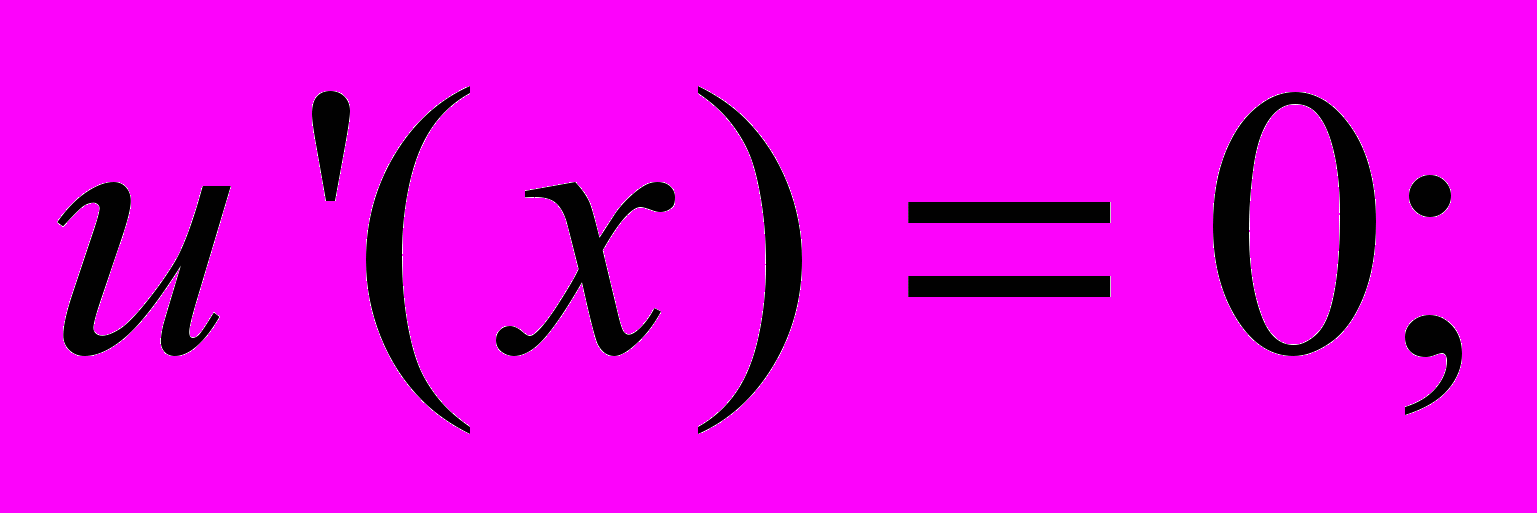
При этом на открытом рынке в условиях конкуренции наибольшей ценой будут обладать объекты, состоящие из элементов сравнения с такими численными показателями количества благ, при которых полезность одной единицы блага будет максимальной. Другими словами, наибольшей ценой будут пользоваться объекты с наименьшим функциональным износом (схожие по остальным характеристикам).

Данное значение показателя количества благ может быть определено путем мониторинга первичного рынка объектов, аналогичных объекту оценки (объекты, выставленные на продажу на первичном рынке, обладают наименьшим функциональным износом, так как в этом случае производитель (продавец) обладает наиболее актуальной информацией о спросе на дату создания (предложения) данного объекта), как наиболее типичное значение показателя количества благ, анализируемого элемента сравнения (см. рисунок 2). Так же оно может быть определено экспертным путем, как наиболее популярное, по мнению эксперта (экспертов), на первичном рынке значение показателя количества благ, анализируемого элемента сравнения. Кроме того, данные о типичных характеристиках объектов, предлагаемых производителями (продавцами) на первичном рынке, могут приводиться в регулярно издаваемых аналитических обзорах рынка.

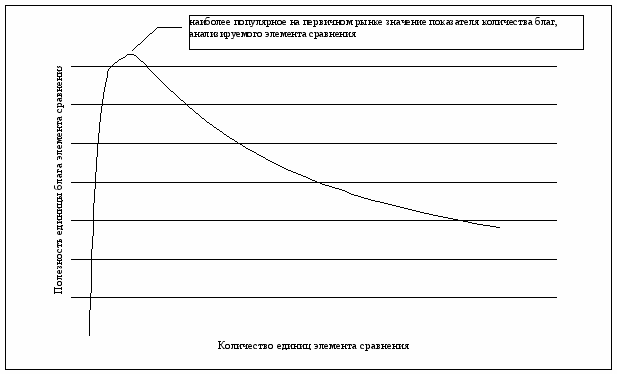Рис. 2. График зависимости полезности единицы блага элемента сравнения от количества единиц сравнения

Обозначим значение единиц блага, при которых функция полезности единицы блага достигает максимума через x_T (x_T > 0). Функция полезности единицы блага будет иметь в данной точке экстремум:



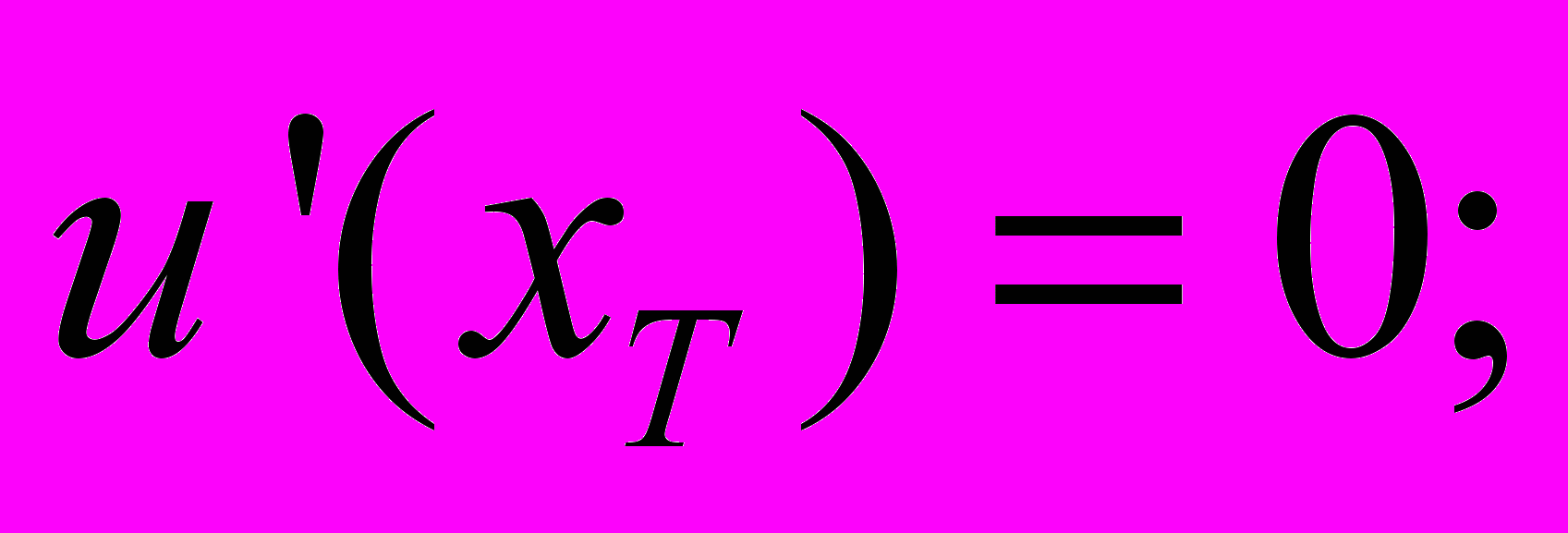
Так как:





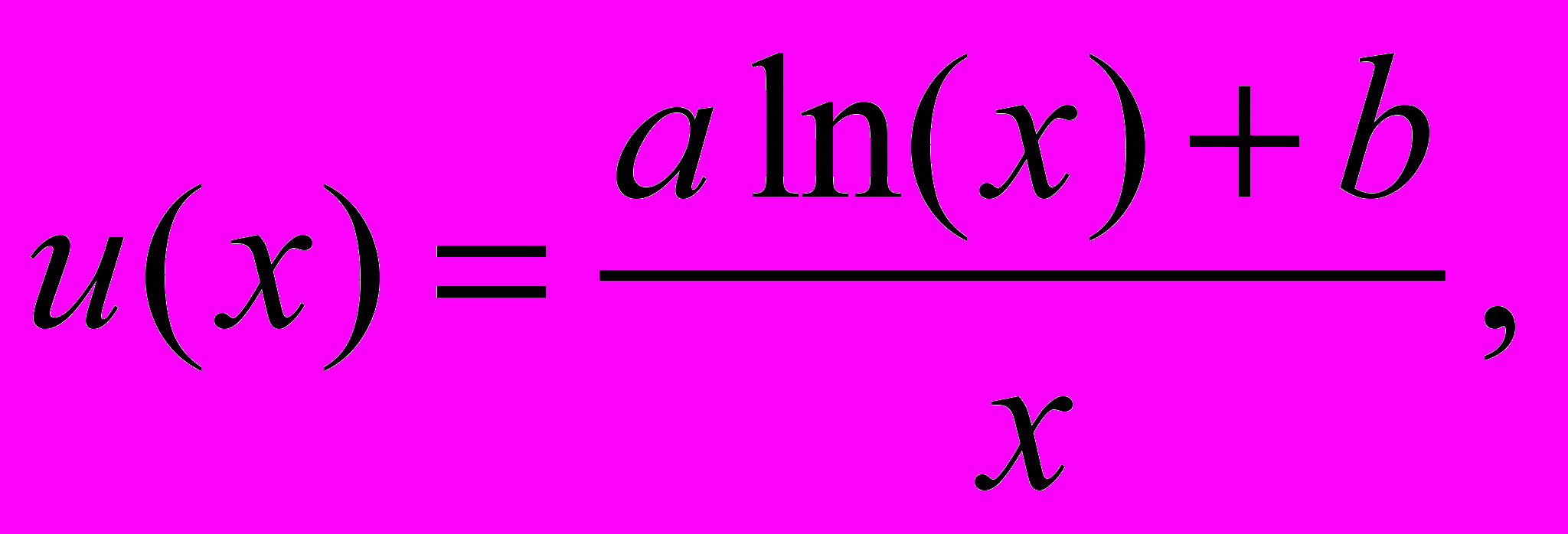
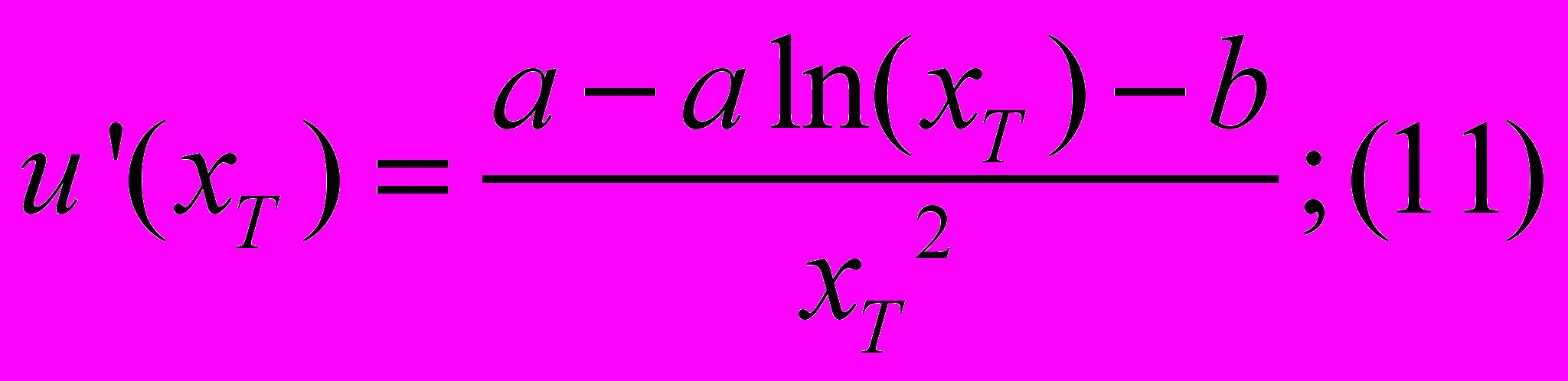
Тогда:




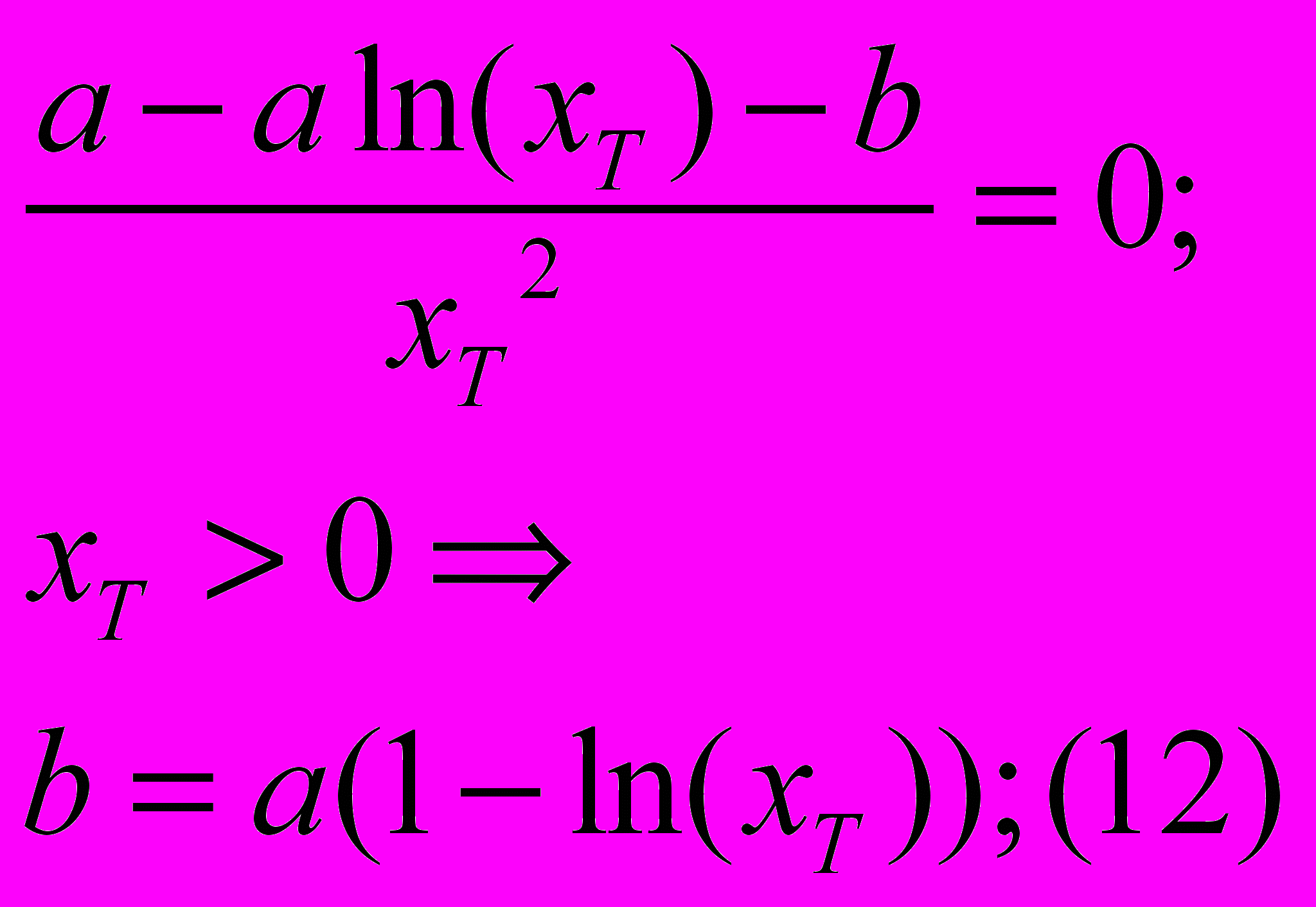
Подставив значение параметра b в уравнение (8) и (9), получим:





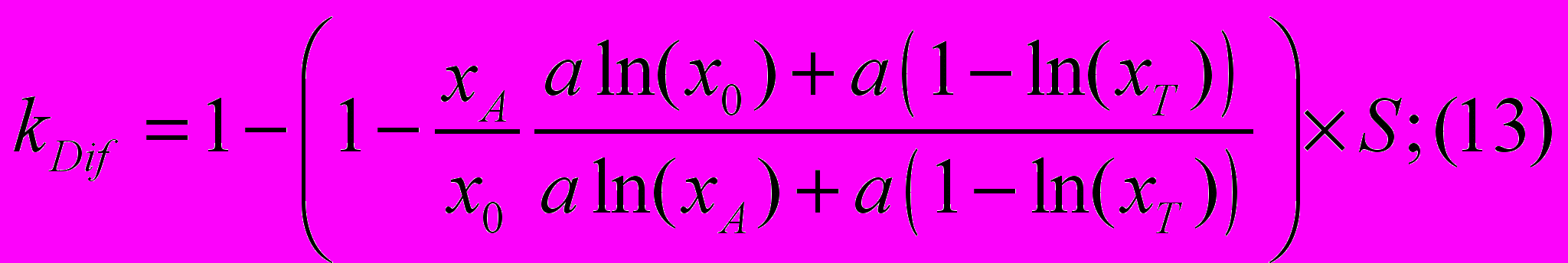
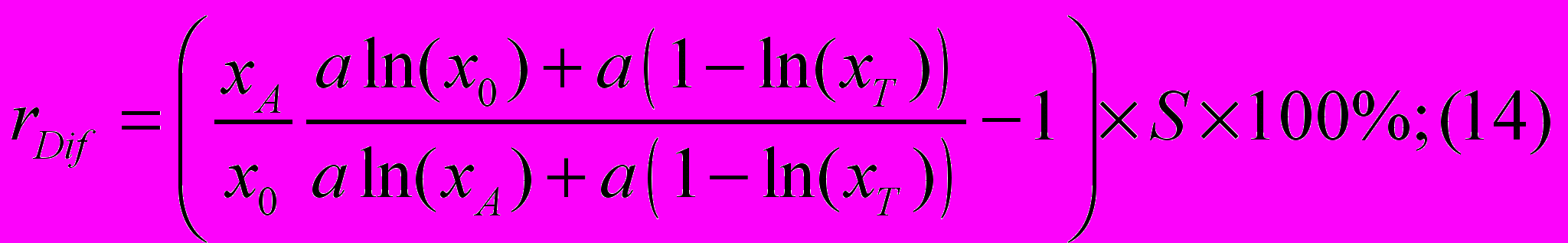
Откуда:






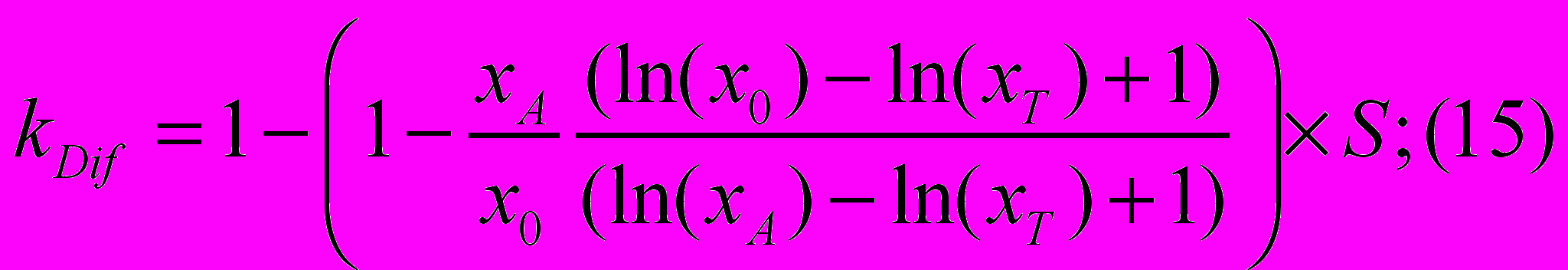
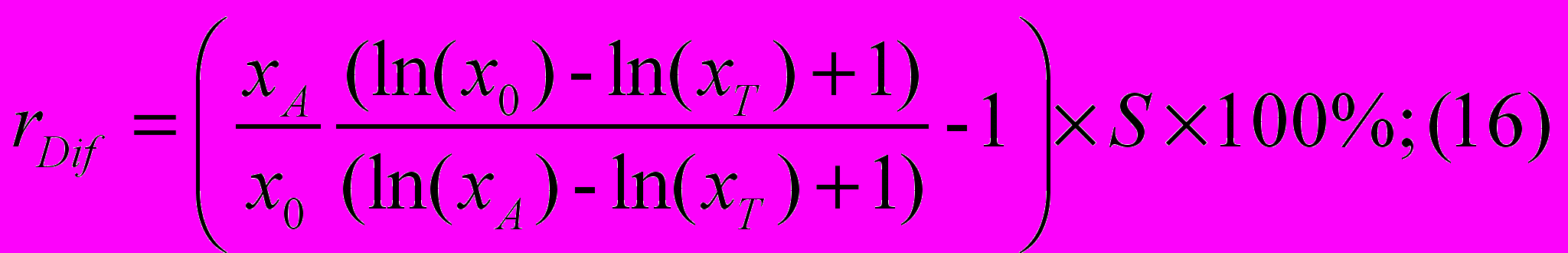
Примером применения полученных формул (15), (16) может служить определение корректировки на разницу в площадях кухонь в трехкомнатных квартирах. Так, например, площадь кухни в оцениваемой квартире составляет 9 кв. м (при общей площади квартиры 70 кв. м). Пусть на основе мониторинга рынка вновь возводимого жилья установлено, что в настоящее время наиболее часто на первичном рынке жилья в трехкомнатных квартирах встречаются площади кухонь равные 14 кв. м. Площадь кухни объекта-аналога составляет 11 кв. м при общей площади квартиры – 68 кв. м.

x_T = 14 кв. м;

x₀ = 9 кв. м;

x_А = 11 кв. м;

Тогда, подставив указанные значения в формулы (15) и (16), получим:

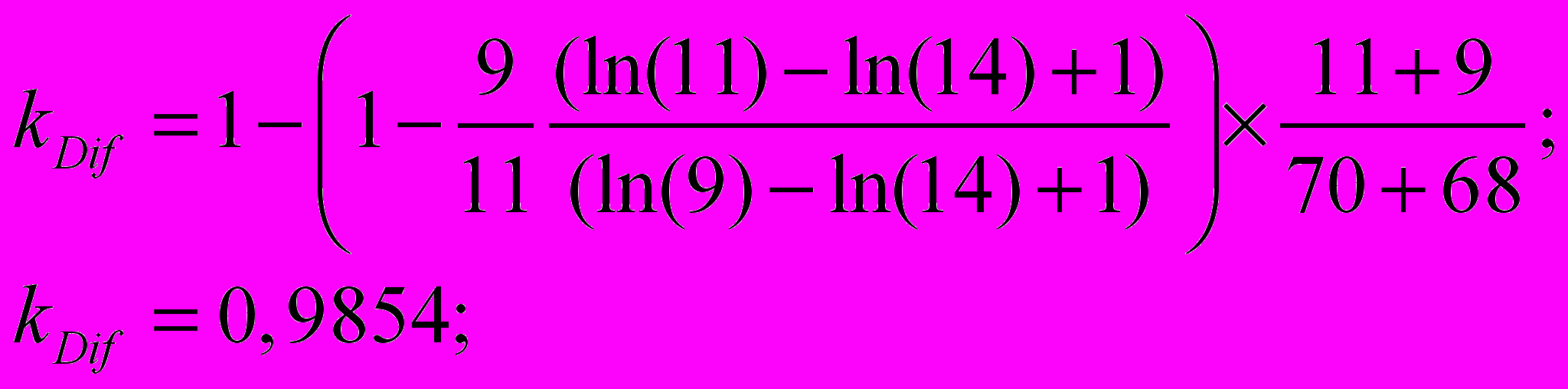
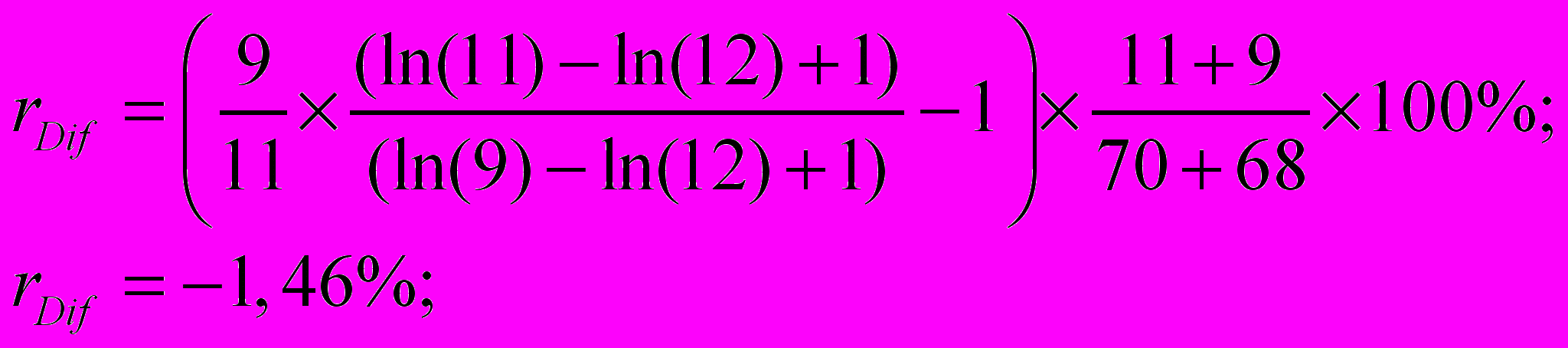
Таким образом, искомая корректировка составляет: минус 1,46%, соответствующий корректировочный коэффициент – 0,9854.

Возможны случаи, когда пользующееся наибольшим спросом на рынке значение элемента сравнения не является строго определенным параметром, а находится в некоем интервале. Рассмотрим эти случаи.

Пусть существует множество различных функций полезности, вида u(x) ~ ln(x) с различными значениями x_T, при которых полезность единицы сравнения является максимальной. Каждое подмножество из данного множества характеризует финансовое поведение определенной группы людей. При этом рыночную стоимость, как наиболее вероятную цену, по которой объект оценки может быть отчуждён на открытом рынке в условиях конкуренции, формирует наиболее многочисленная группа, то есть множество с наибольшим кардинальным числом. Данный вывод вытекает из того обстоятельства, что при равномерном распределении вероятности, вероятность события, соответствующего элементу множества, обладающего наибольшей мощностью, является максимальной. При этом если существует несколько равномощных множеств, может существовать множество различных значений x_T, при которых полезность единицы сравнения является максимальной для различных групп людей, то есть .

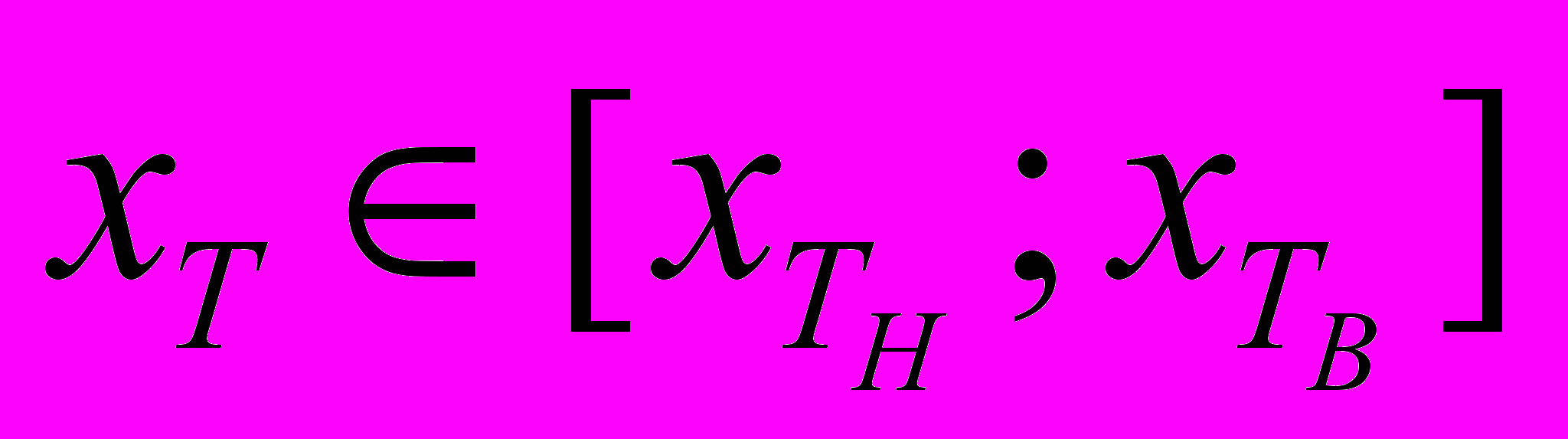Осведомленный, действующий разумно, располагающий всей необходимой информацией, продавец будет стремиться получить наибольшую выгоду от реализации объекта оценки на открытом рынке. С другой стороны, так как существует множество различных значений x_T, при которых полезность (а значит и стоимость) единицы сравнения является максимальной для различных групп людей, продавец будет ориентироваться на ту группу, для которой значение x_T объекта оценки будет наиболее близким к значениям x₀ (x_A). Таким образом, в случае, если существует некоторое множество функций полезности, для которых полезность единицы сравнения является максимальной при различных значениях x_T, в расчетах принимается такие значения 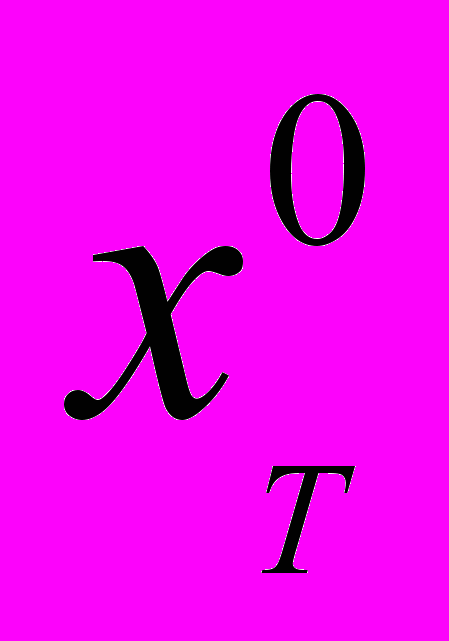и 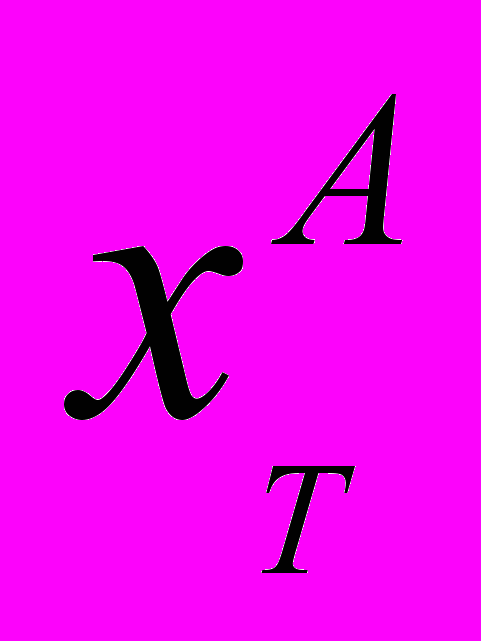, которые соответствуют следующим условиям: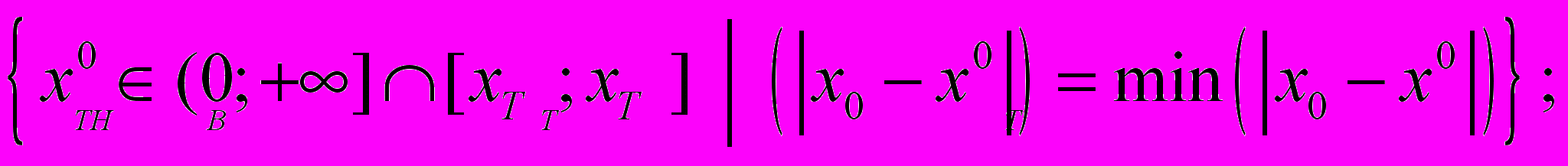



и

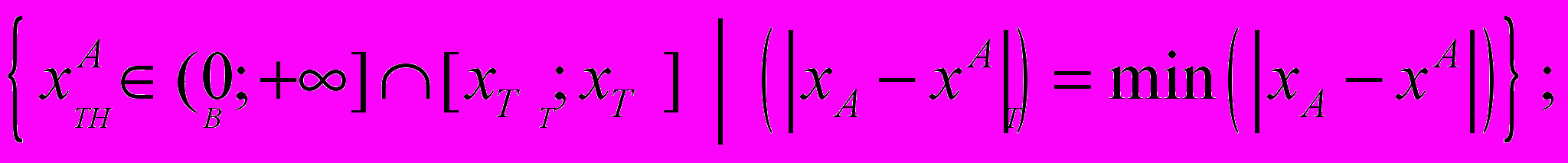
где,

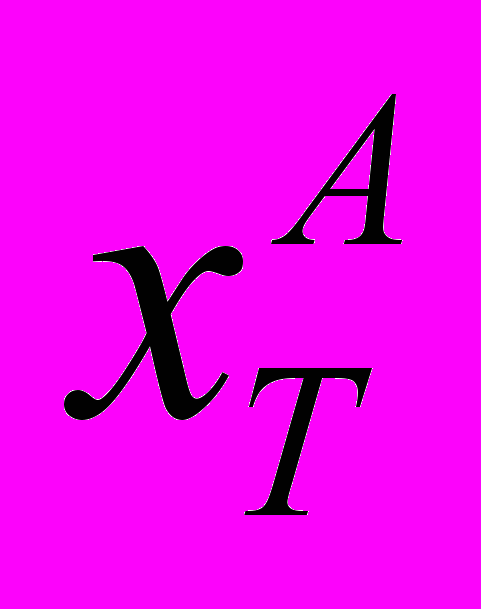– значение элемента сравнения, при котором полезность объекта-аналога является максимальной;

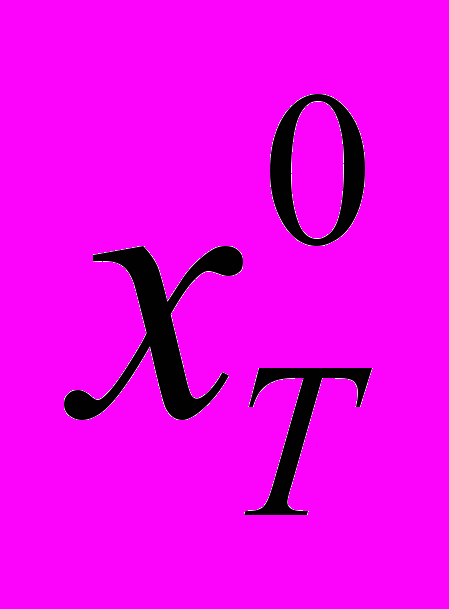– значение элемента сравнения, при котором полезность объекта оценки является максимальной;

Тогда для группы людей, для которых функция полезности приобретает максимальное значение при значении переменной 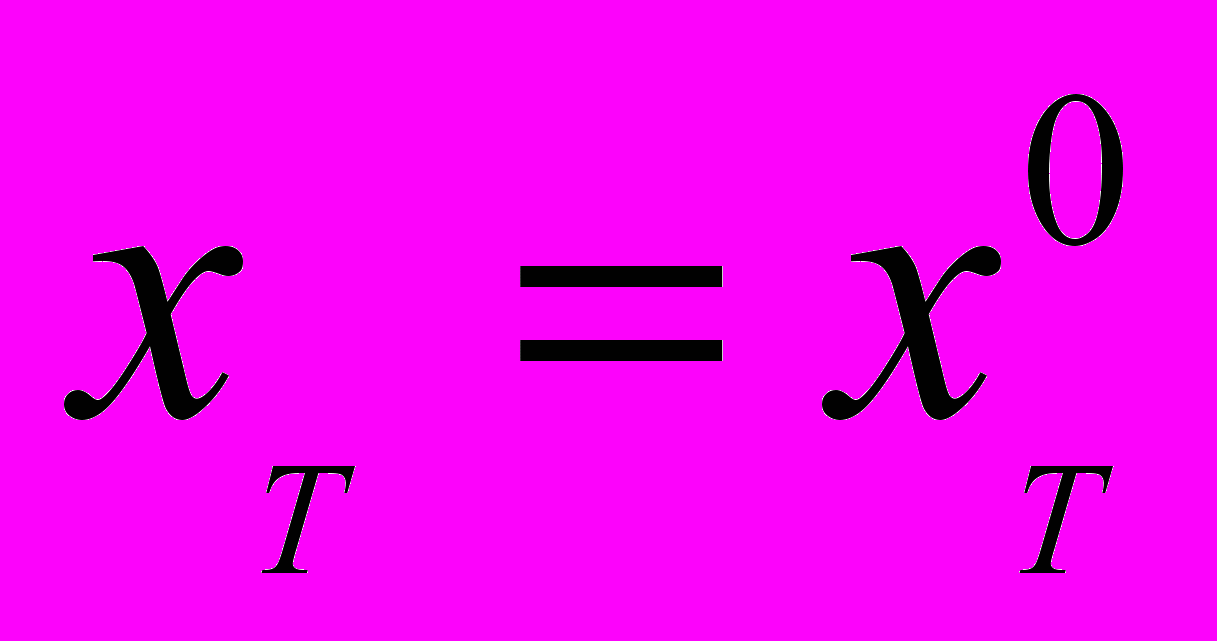, отношение полезности единицы элемента сравнения объекта оценки к единице элемента сравнения объекта аналога составит: 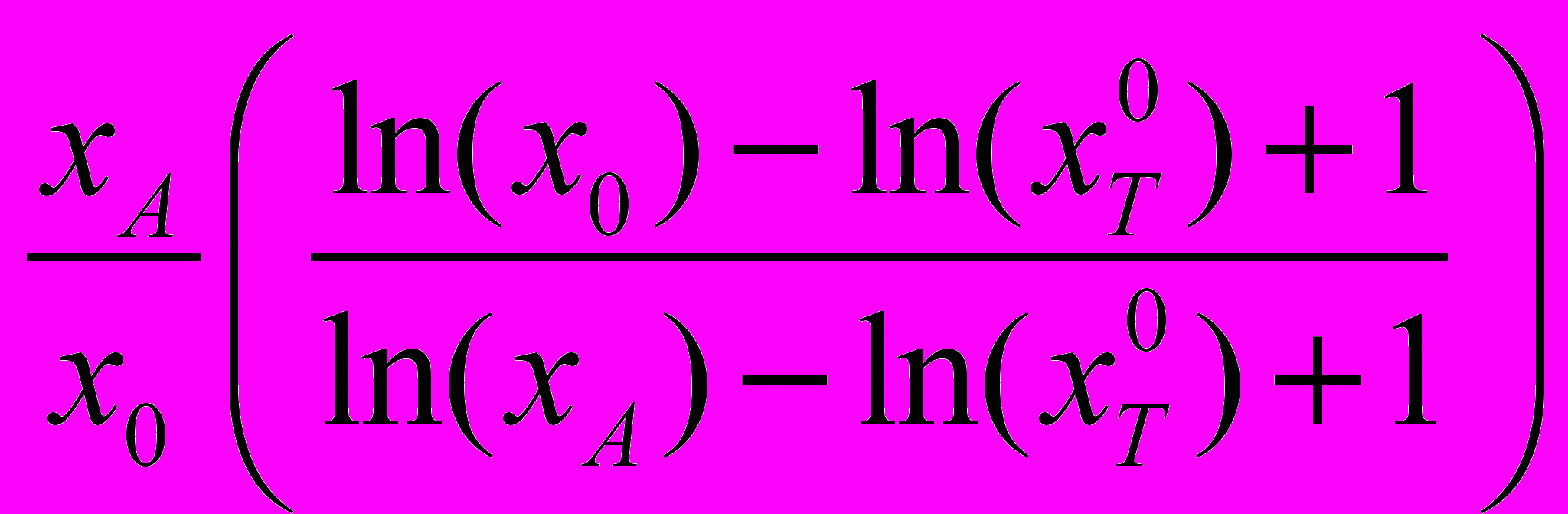, а соответствующая корректировка: 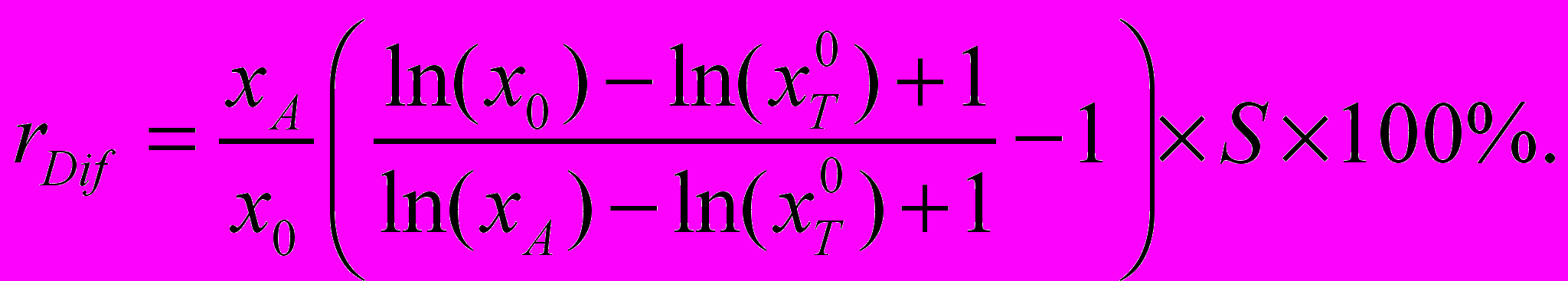Для группы людей, для которых функция полезности приобретает максимальное значение при значении переменной 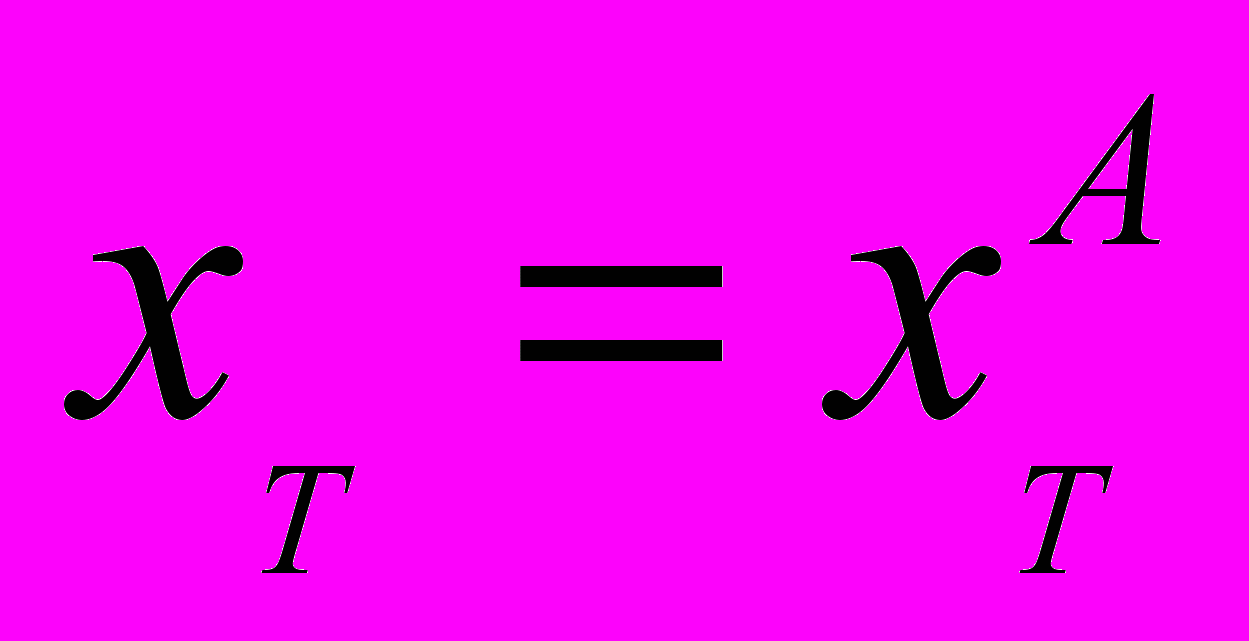, данное отношение соответственно составит: 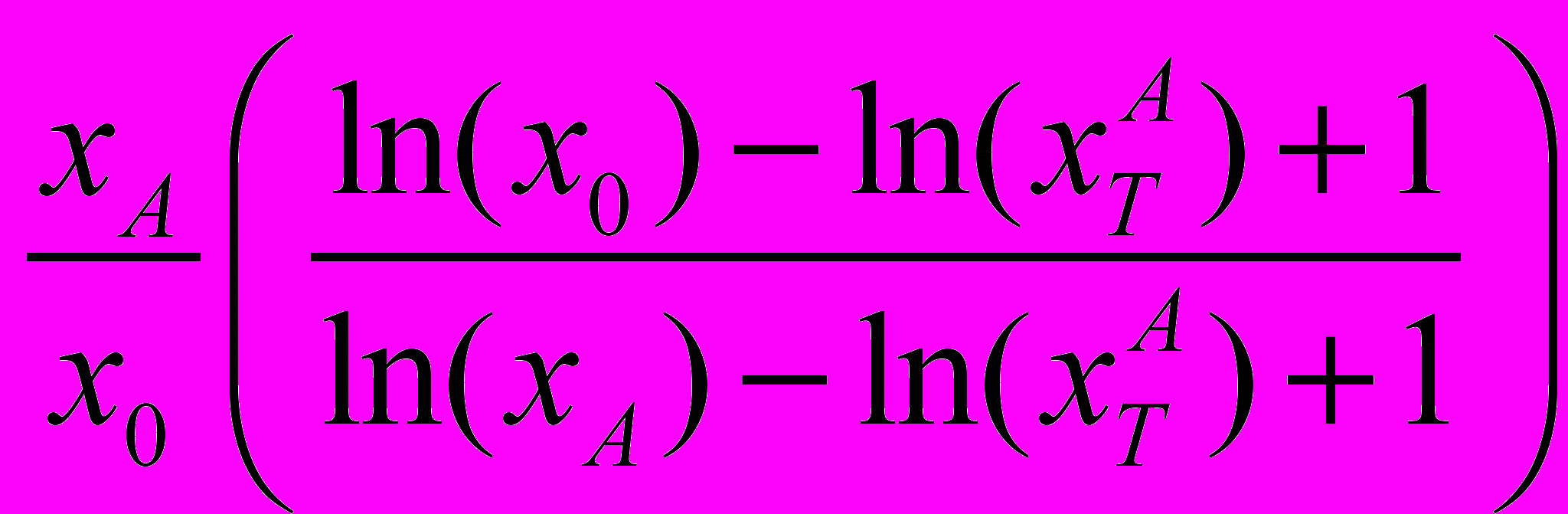, а корректировка –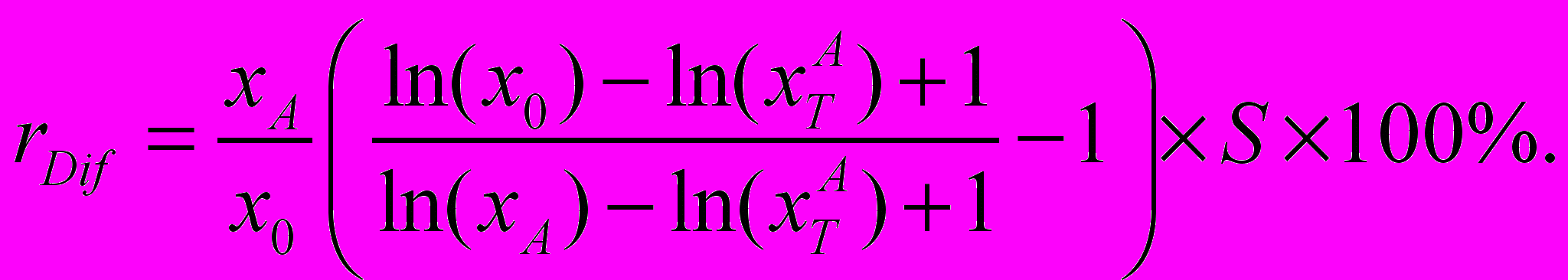

Так как мощность множеств людей составляющих данные группы равна, формула (16) приобретает вид:

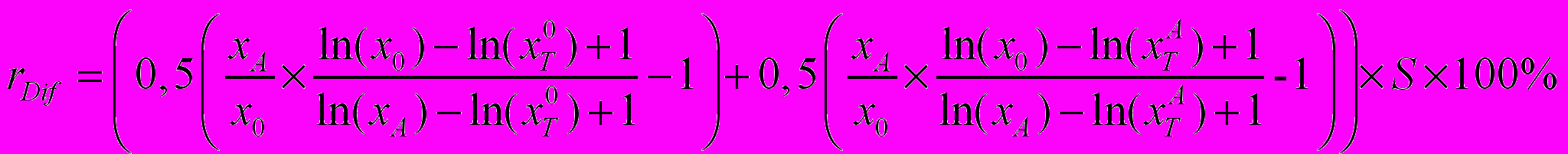или: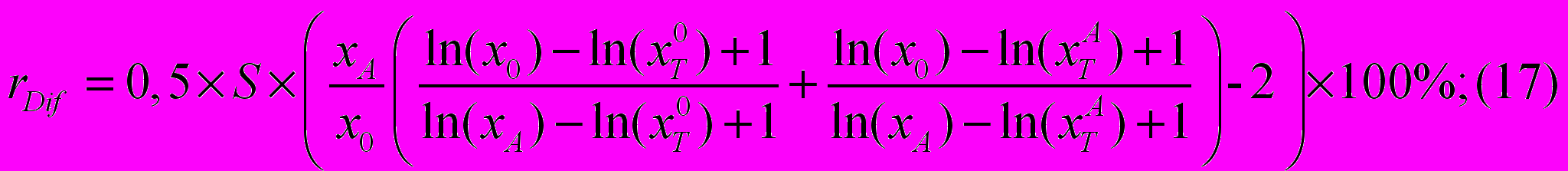



Следуя тем же размышлениям, получаем формулу для определения поправочного коэффициента для случая, когда значение элемента сравнения находится в интервале :




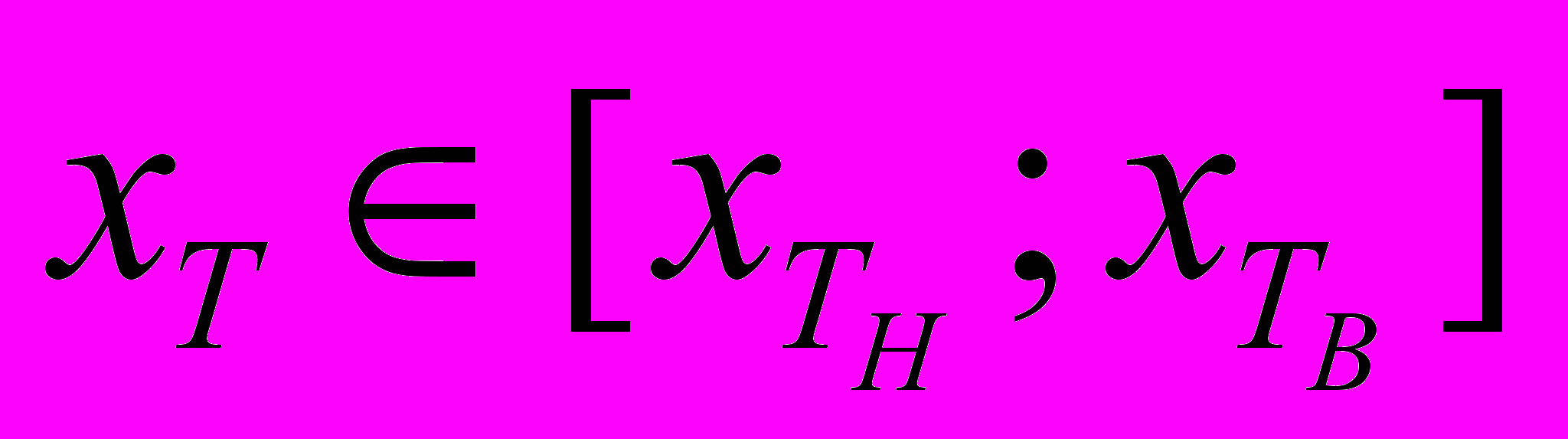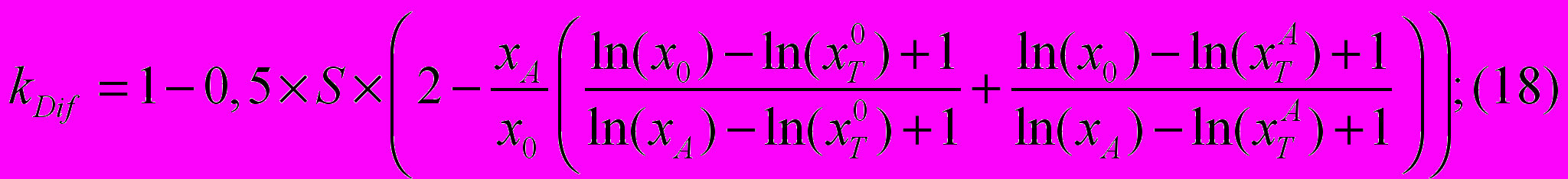
Возможность практического применения данных формул: (17) и (18) – можно проиллюстрировать на следующем примере. Пусть дан земельный участок с распложенным на нём складским зданием, площадью 1200 кв. м. Известно, что стоимость земельного участка составляет около 30% от стоимости всего единого объекта недвижимого имущества. Известно также, что наибольшей популярностью пользуются склады площадью 1000 – 3 000 кв. м (для простоты будем считать, что площадь застройки равна площади земельного участка, на котором расположено здание). Площадь земельного участка под складским зданием объекта-аналога составляет 900 кв. м.

Необходимо вычислить корректировку на площадь земельного участка под складским помещением.

Так как 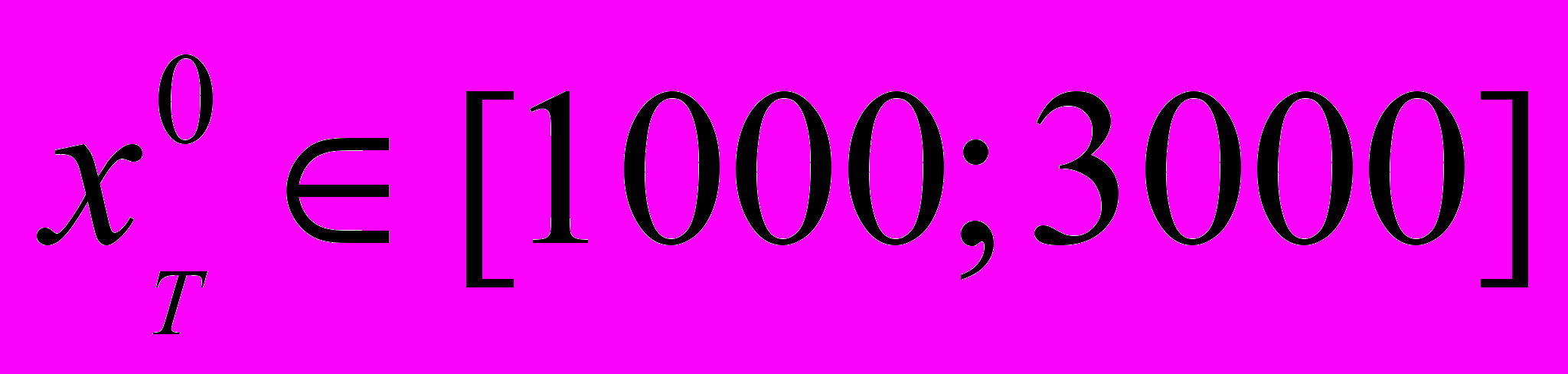, 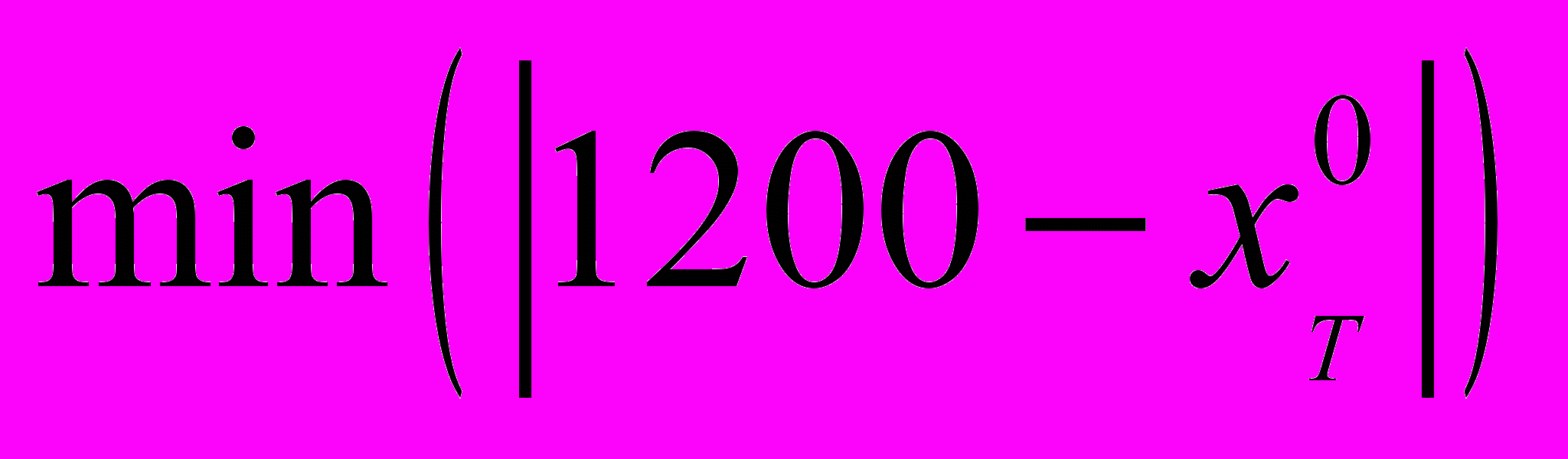достигается при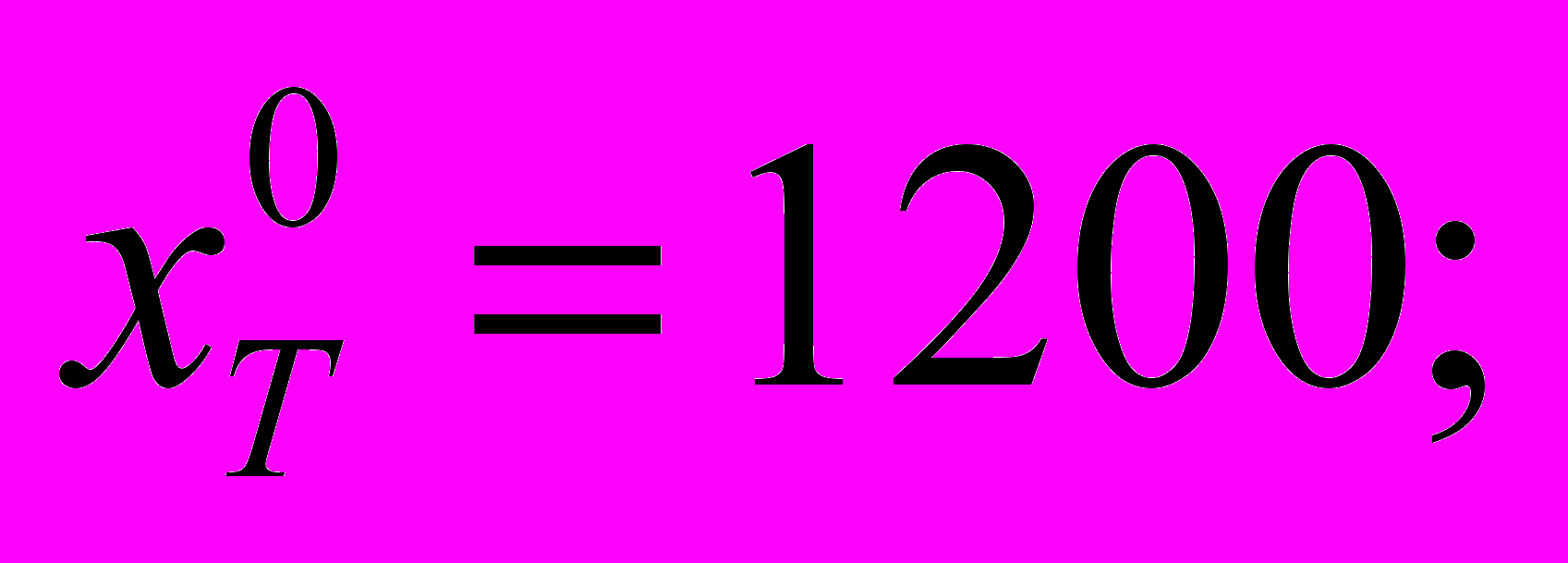

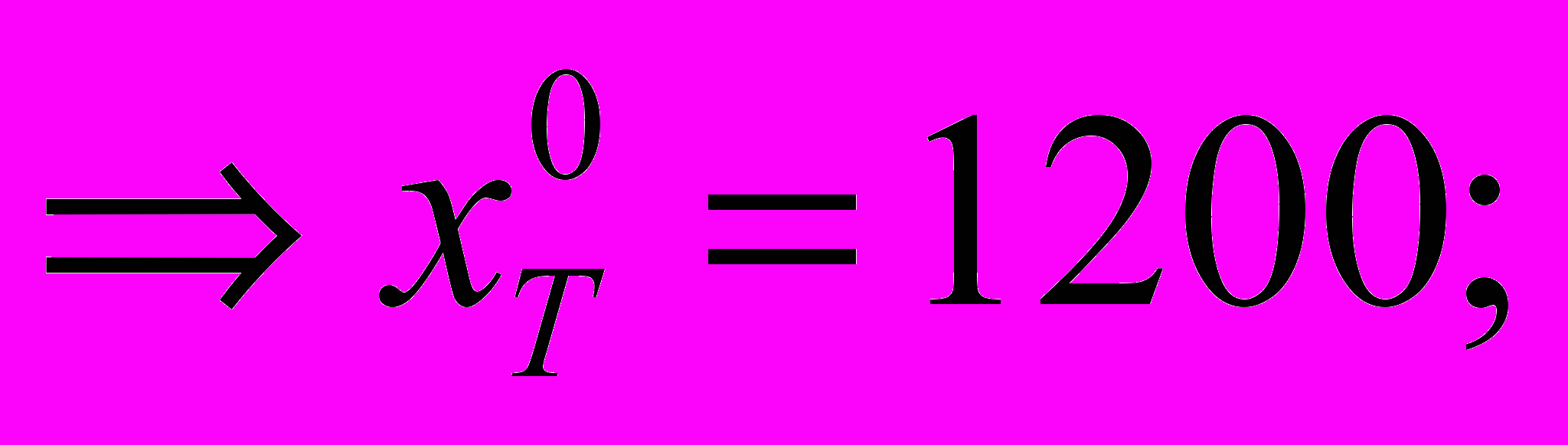
Так как 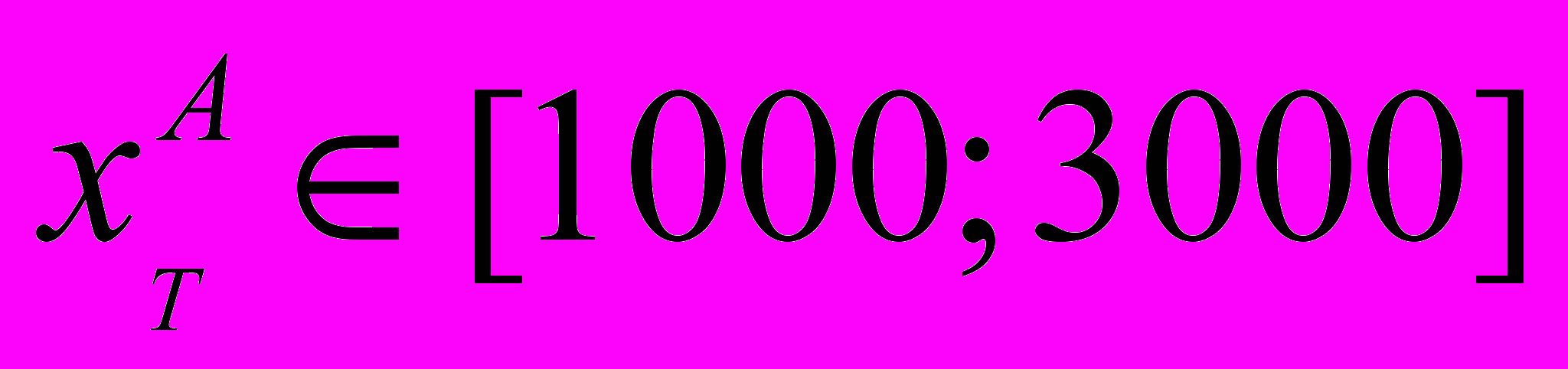, 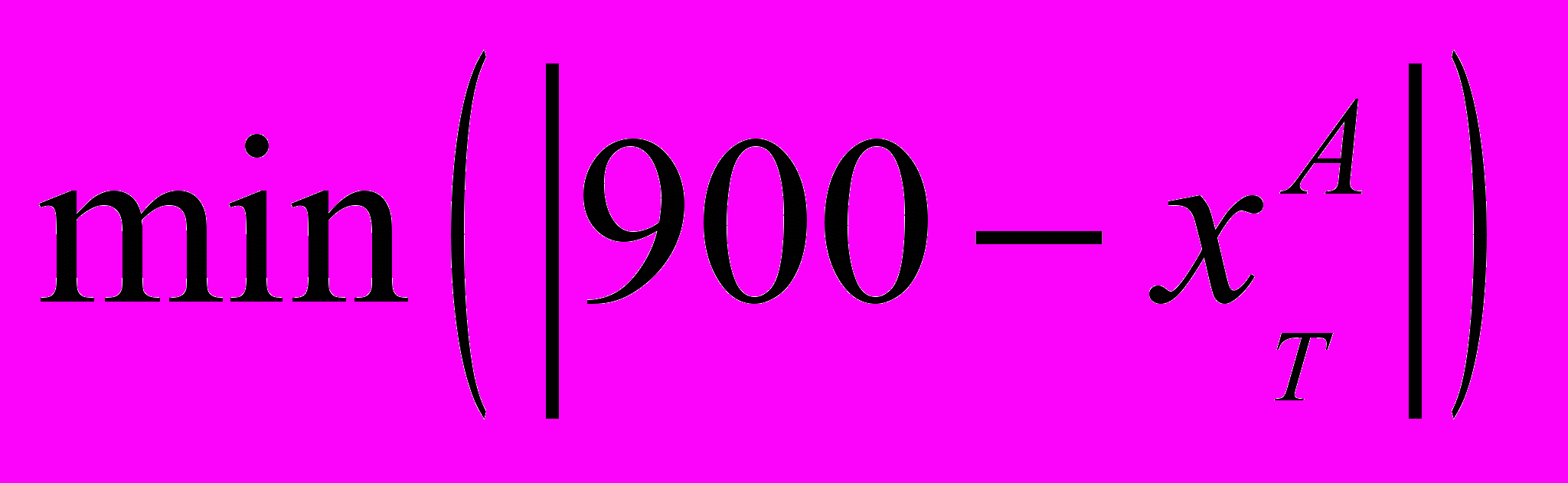достигается при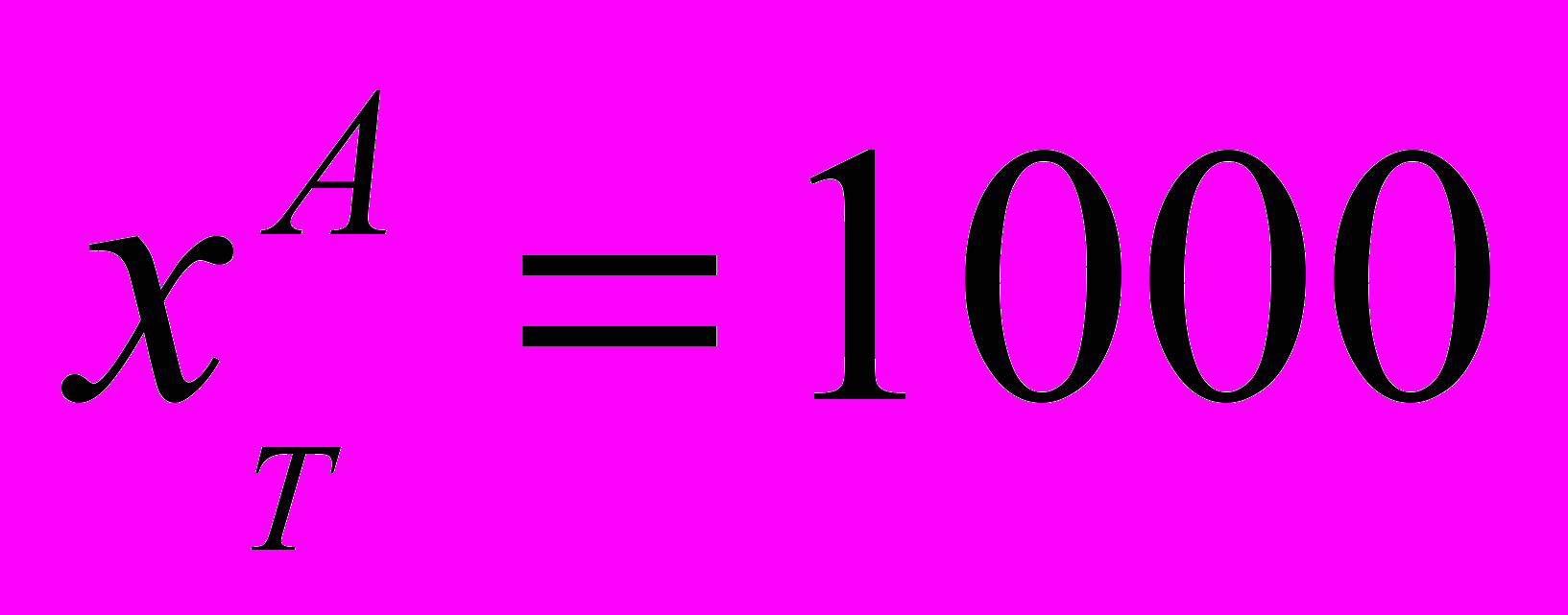

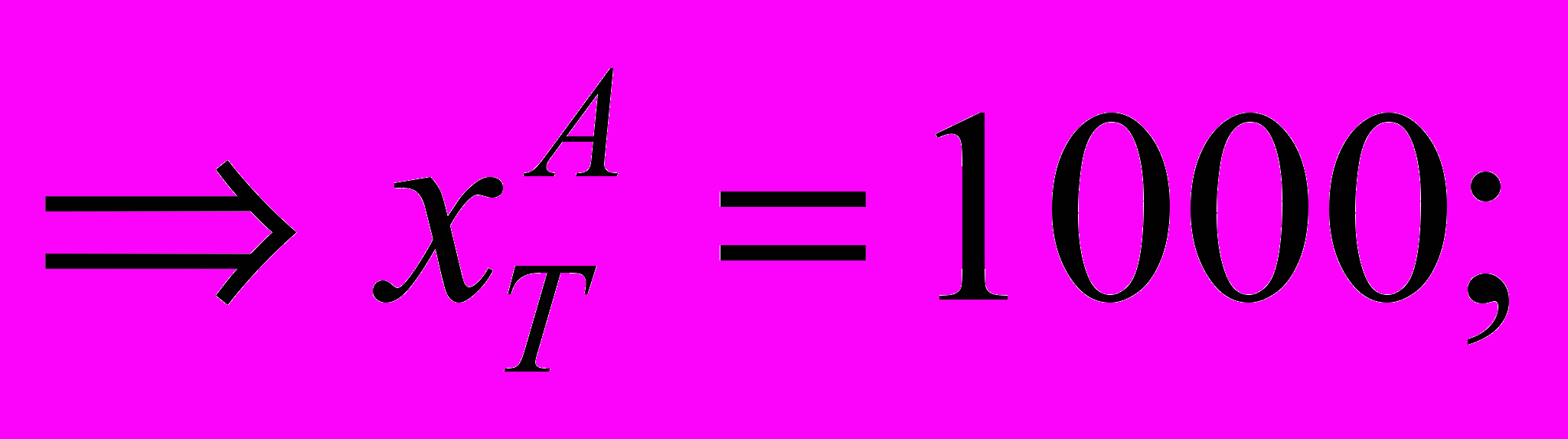
Тогда поправочный коэффициент равен:



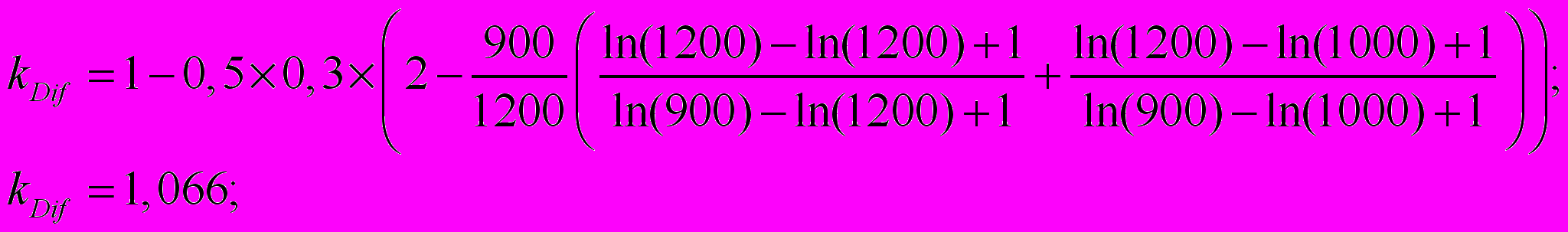
Соответствующая корректировка составляет:




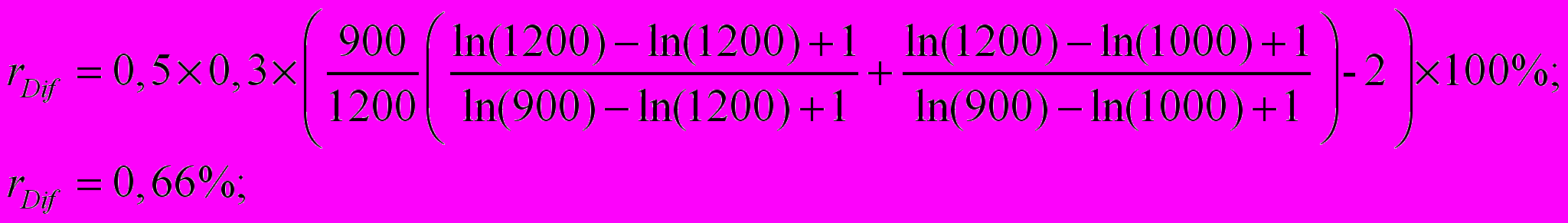
Выводы

1. Корректировочный коэффициент k_Dif и относительная корректировка r_Dif на различия в численных значениях элементов сравнения на основе функции полезности может быть определена по следующим формулам:





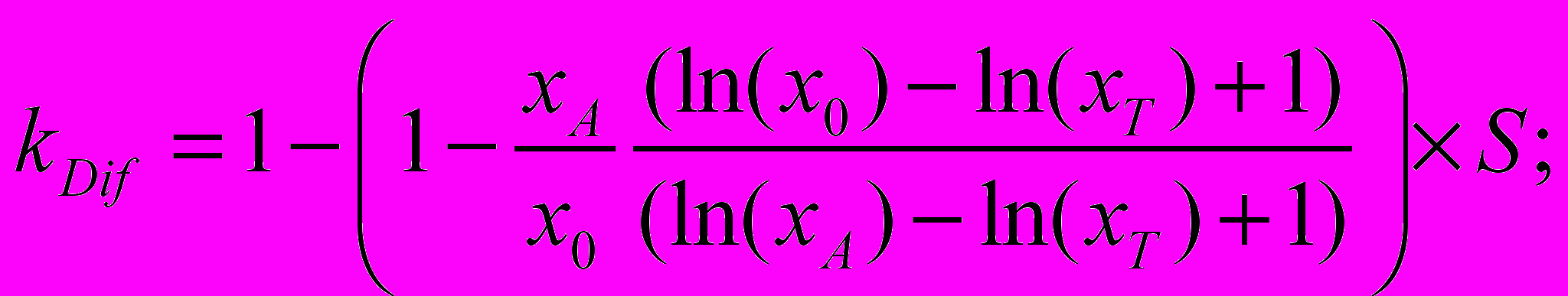
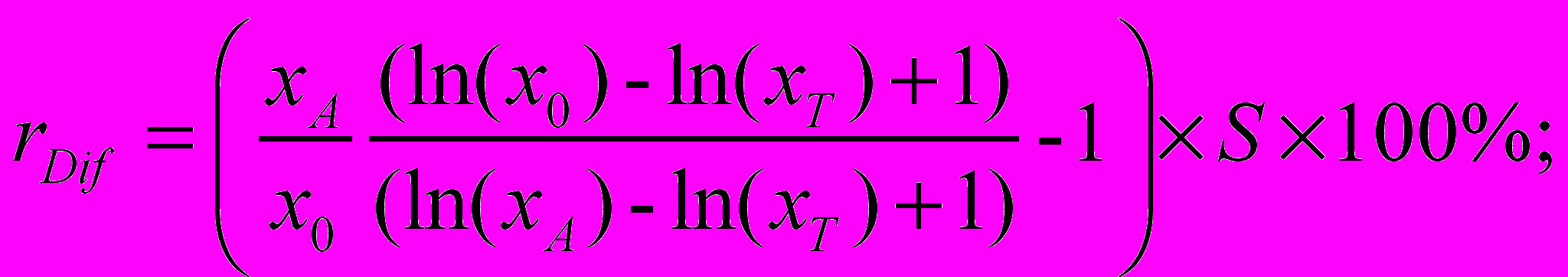
x₀ – количество единиц блага элемента сравнения объекта оценки;

x_A – количество единиц блага элемента сравнения объекта-аналога;

x_T – количество единиц блага элемента сравнения, при которых функция полезности единицы блага достигает своего максимума;



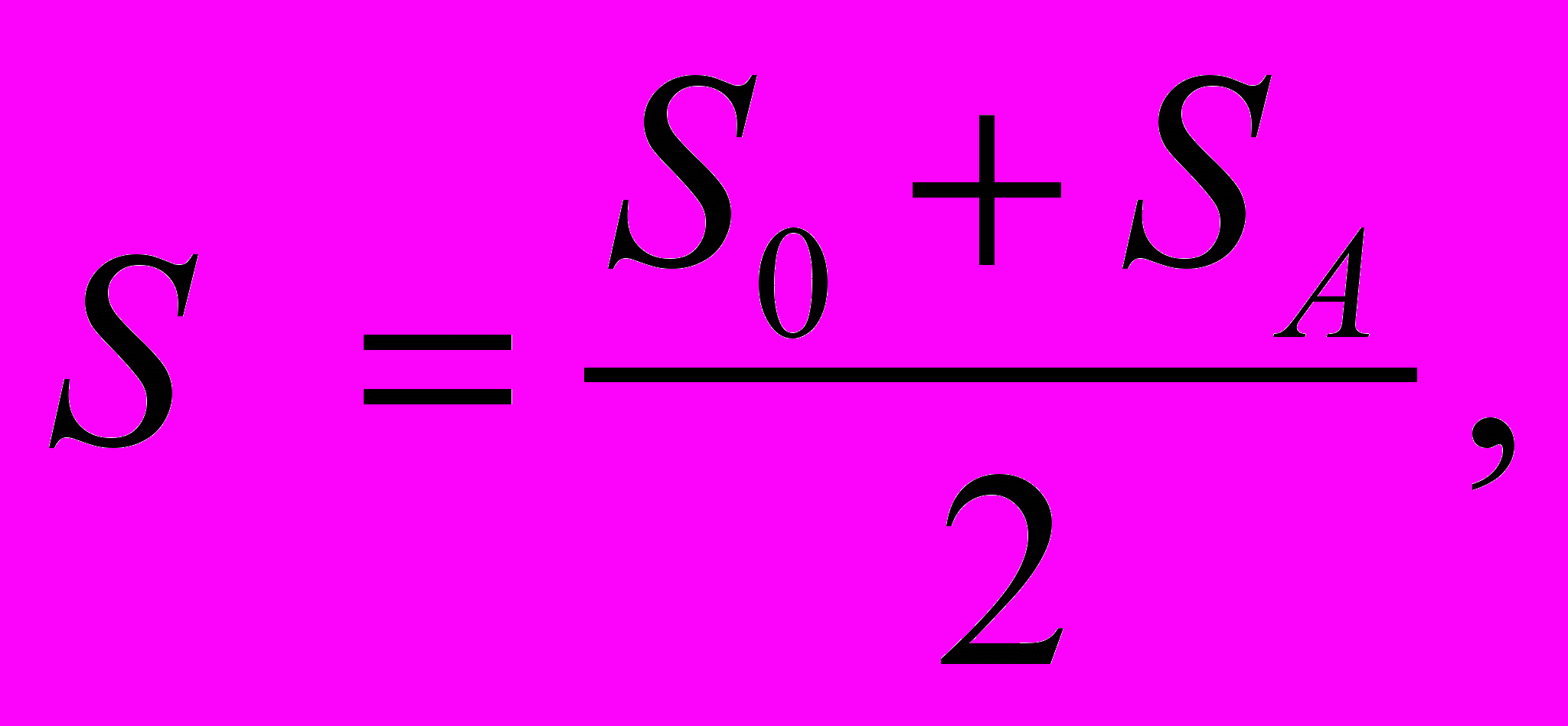
S₀ – доля элемента сравнения объекта оценки в его общей стоимости;

S_A – доля элемента сравнения объекта-аналога в его общей стоимости;

2. Значение x_T может быть определено:

• путем мониторинга первичного рынка объектов, аналогичных объекту оценки, как пользующееся наибольшим спросом на первичном рынке количество единиц блага элемента сравнения. Обоснованием данного выбора является то обстоятельство, что производитель нового объекта обладает наиболее актуальной информацией о спросе на дату создания (предложения) данного объекта. Другими словами новый объект, предлагаемый на первичном рынке, будет обладать наименьшим функциональным износом;
  
• экспертным путем, как наиболее популярное на первичном рынке значение показателя количества благ, анализируемого элемента сравнения;
  
• путем анализа регулярно издаваемых аналитических обзоров первичного рынка объектов, аналогичных объекту оценки.
  

3. Для случаев, когда пользующееся наибольшим спросом на рынке значение элемента сравнения не является строго определенным параметром, а находится в некоем интервале 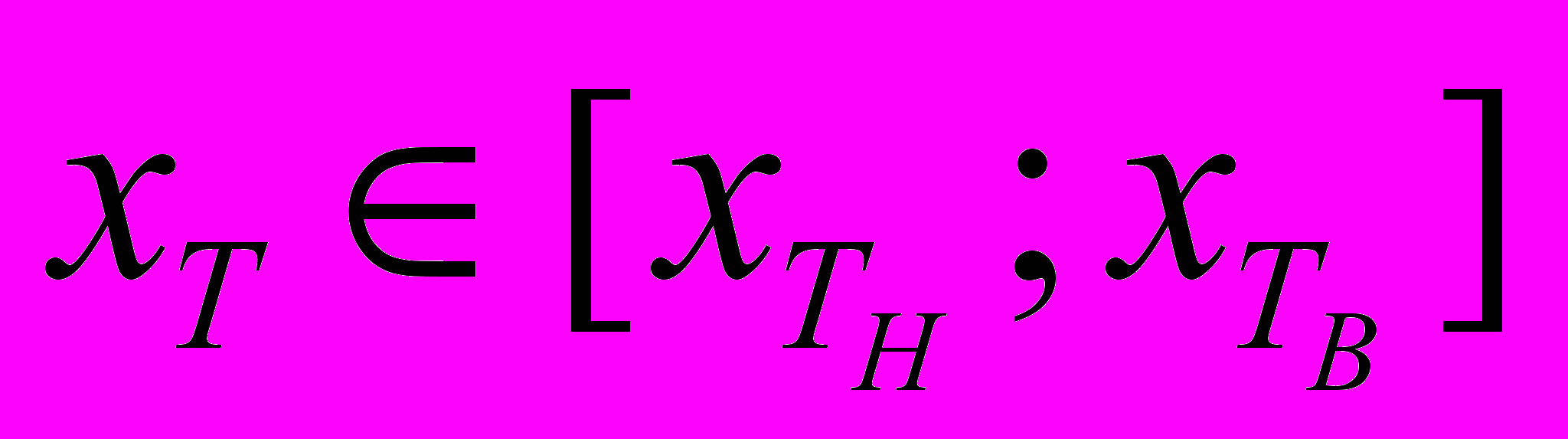, корректировочный коэффициент k_Dif и относительная корректировка r_Dif на различия в численных значениях элементов сравнения на основе функции полезности может быть определена по формулам, приведенным ниже: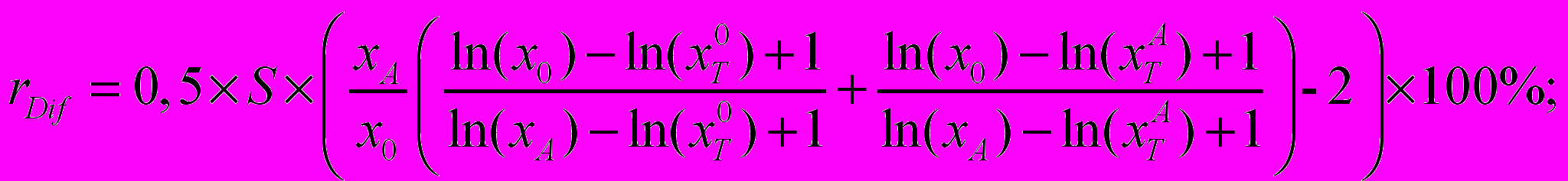





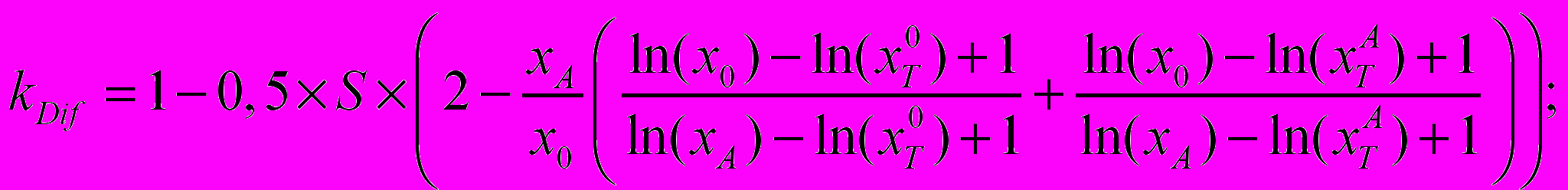
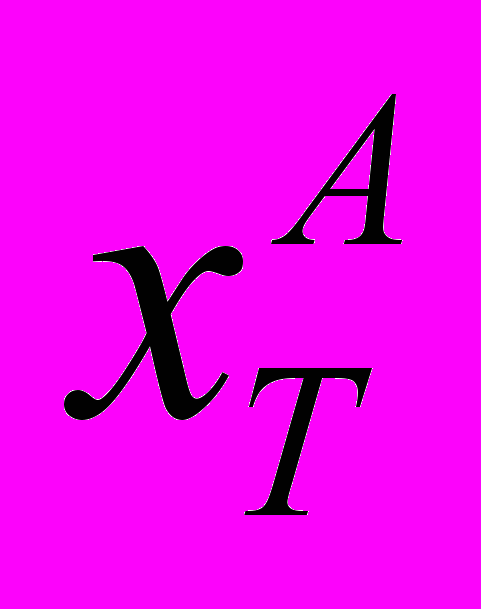– значение элемента сравнения, при котором полезность объекта-аналога является максимальной;

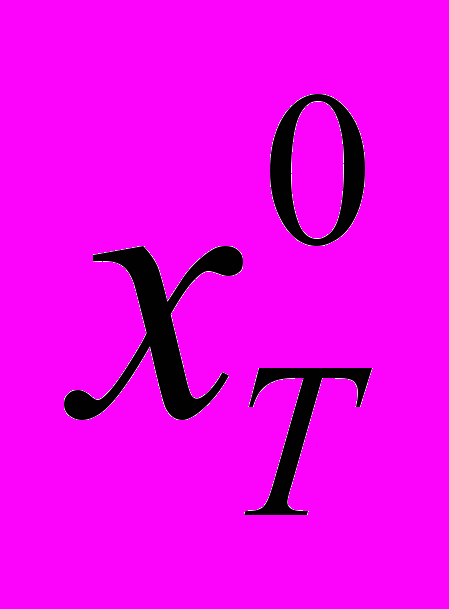– значение элемента сравнения, при котором полезность объекта оценки является максимальной;

При этом в расчетах принимается такие значения 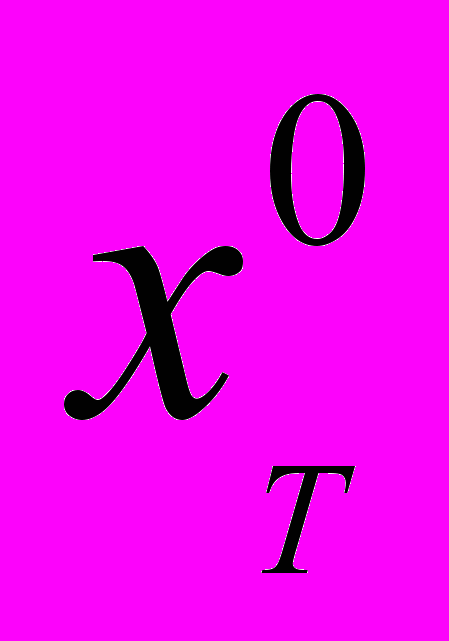и 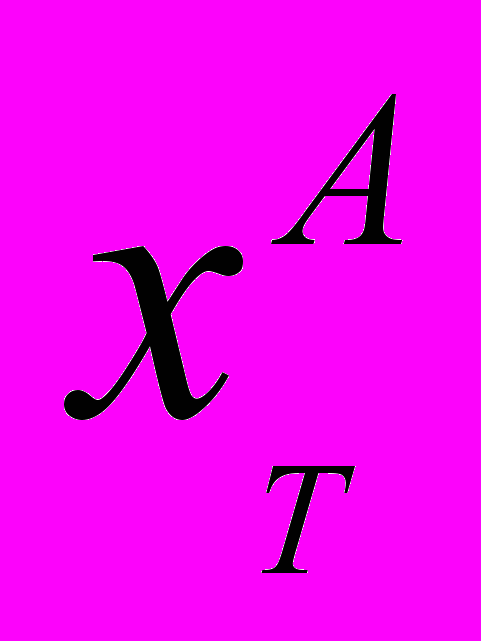, которые соответствуют следующим условиям: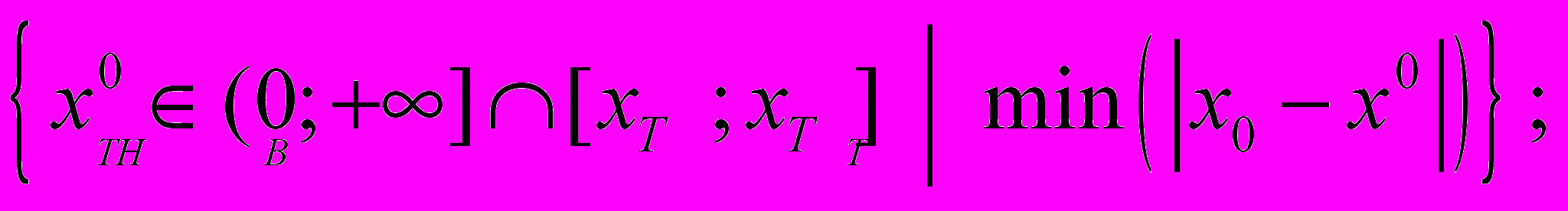



и

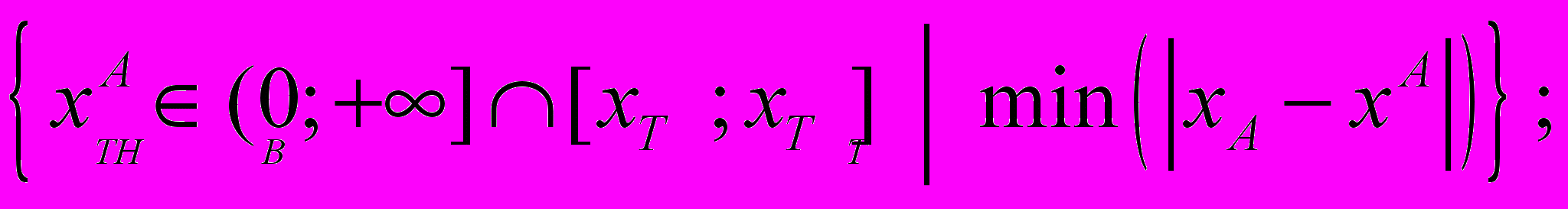
4. Приведенные выше формулы: (15), (16), (17) и (18) – могут быть применены для определения корректировок на различия в численных значениях элементов сравнения. Кроме того, данные формулы могут быть применены для определения величины функционального износа анализируемого элемента сравнения. В этом случае x_T, 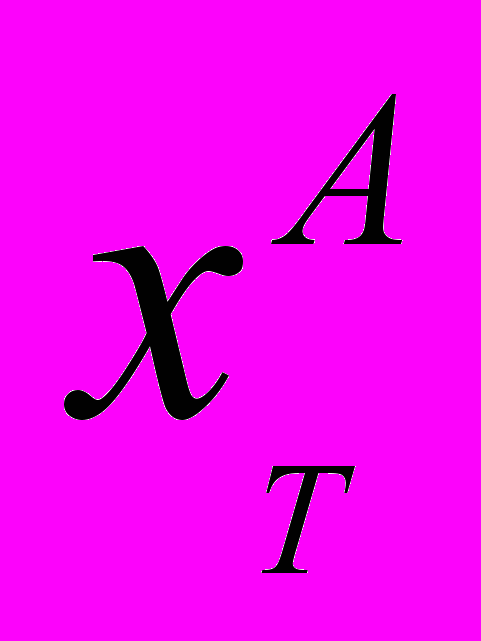, 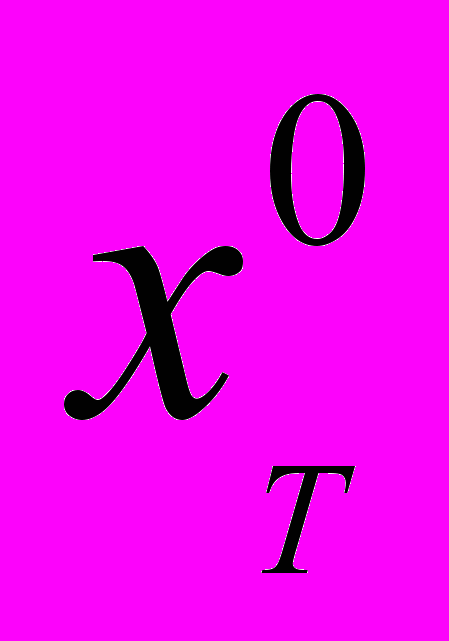– трактуется как количество единиц блага элемента сравнения, при которых функциональный износ, связанный с данным элементом принимает минимальное значение.

5. Рассмотренная выше методика определения корректировок на различия в численных значениях элементов сравнения на основе функции полезности и, приведенные выше формулы: (15), (16), (17) и (18) – позволяют существенно упростить процесс вычисления корректировок при отсутствии, неполноте или недоступности достоверной информации, необходимой для вычисления корректировки на основе традиционных количественных методов определения корректировок.

Список использованной литературы

0. Варламов А. А., Севостьянов А. В. Земельный кадастр. В 6 т. Т. 5 Оценка земли и иной недвижимости. – М.: КолосС, 2006. – 265 с. – (Учебники и учеб. Пособия для студентов высш. Учеб. Заведения).
   
1. Госсена законы / Большая советская энциклопедия. Онлайн-версия БСЭ (3-е издание) на Яндексе [Электронный документ]. - (andex.ru/dict/bse/article/00019/90400.htm). <04.03.2010>
   
2. Лопатников Л. И. Экономико-математический словарь : Словарь современной экономической науки. — 5-е изд., перераб. и доп. — М.: Дело, 2003. — 520 с.
   
3. Математические модели потребительского поведения и спроса / Российский университет Дружбы народов. Официальный сайт [Электронный документ]. - (ities.edu.ru/db/msg/2320). <04.03.2010>
   
4. Примеры основных функций полезности / Банки – новости, информация. Веб-сайт [Электронный документ]. - (ki.ru/text/34). <04.03.2010>