Решение
| Вид материала | Решение |
- Найти частное решение линейного однородного дифференциального уравнения. Решение, 6.09kb.
- «Алгоритмизация и решение физических задач на эвм», 391.8kb.
- Навык 4 Думайте в духе «Выиграл выиграл», 91.19kb.
- Решение, 1036.71kb.
- Решение линейных уравнений Цель урока, 126.51kb.
- Совет депутатов г. Протвино решение от 25. 07. 2011 №241/38, 380.05kb.
- Решение страсбург, 1314.79kb.
- Герция Виталия Михайловича, Садоводческого некоммерческого партнерства «Речник» иОрлова, 141.35kb.
- Первая Вторая половина ХIХ начало ХХ вв. Право и жизнь в адыгском обществе, 3427.05kb.
- Республика мордовия рузаевский муниципальный район совет депутатов городского поселения, 19.08kb.
ЛЕКЦИЯ №3
Пример метода Фибоначчи.
Найти минимум функции
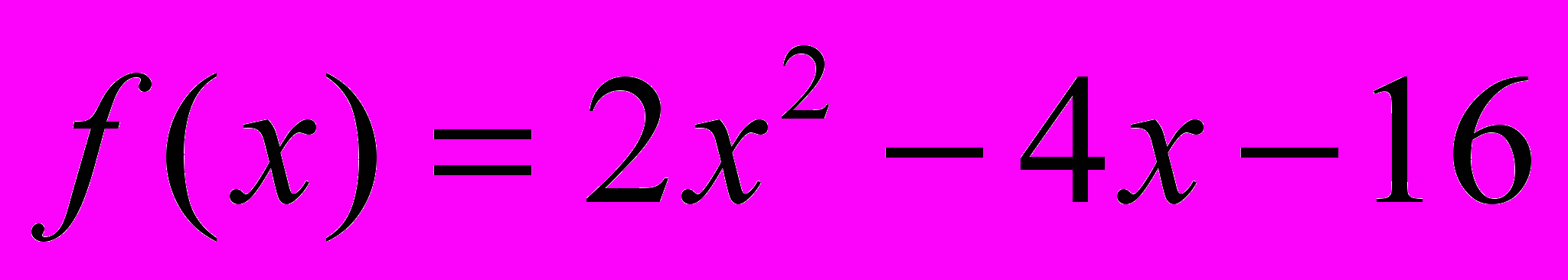на отрезке 
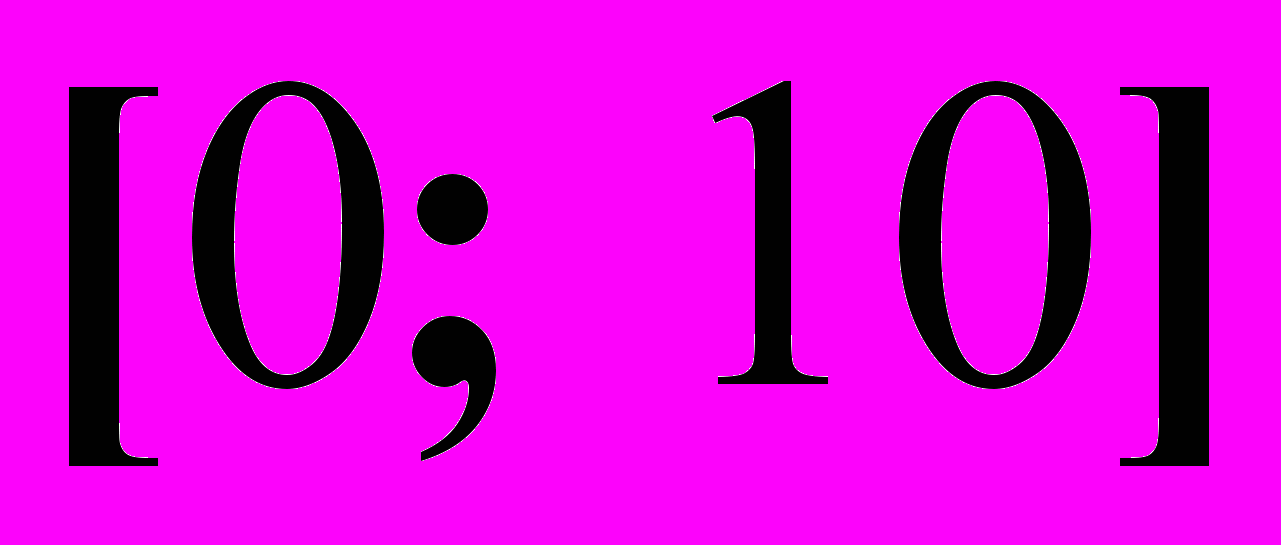за 4 шага.Решение.
, 
, 
, 
, 
, 
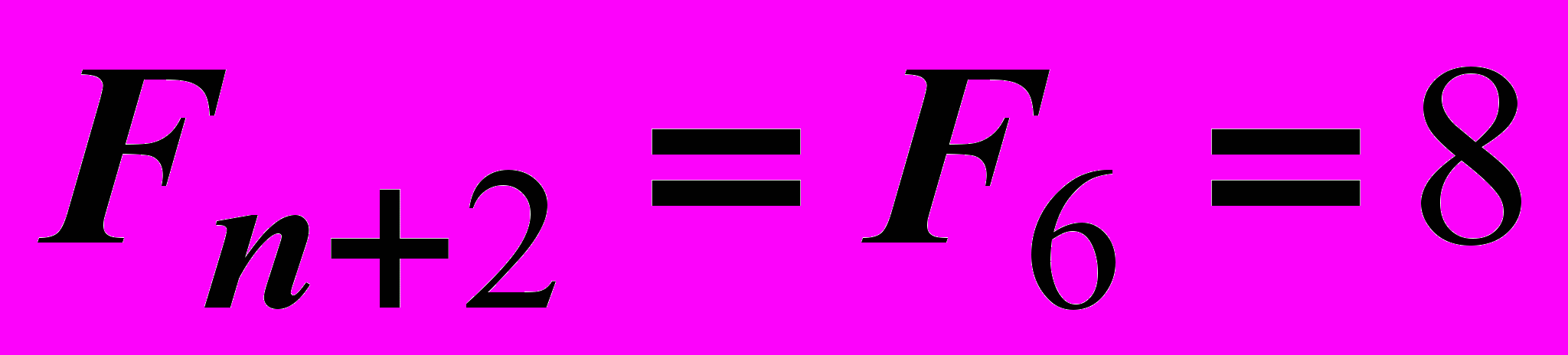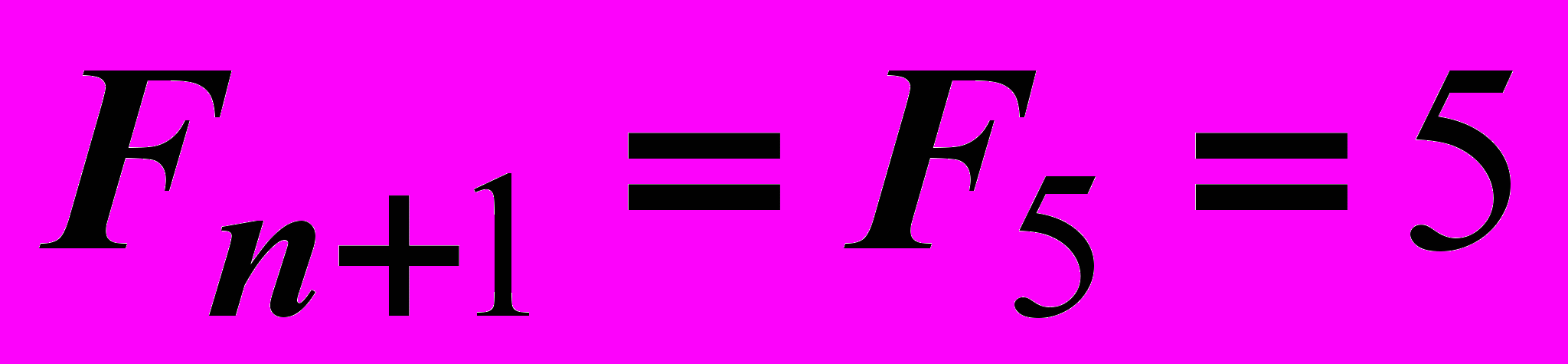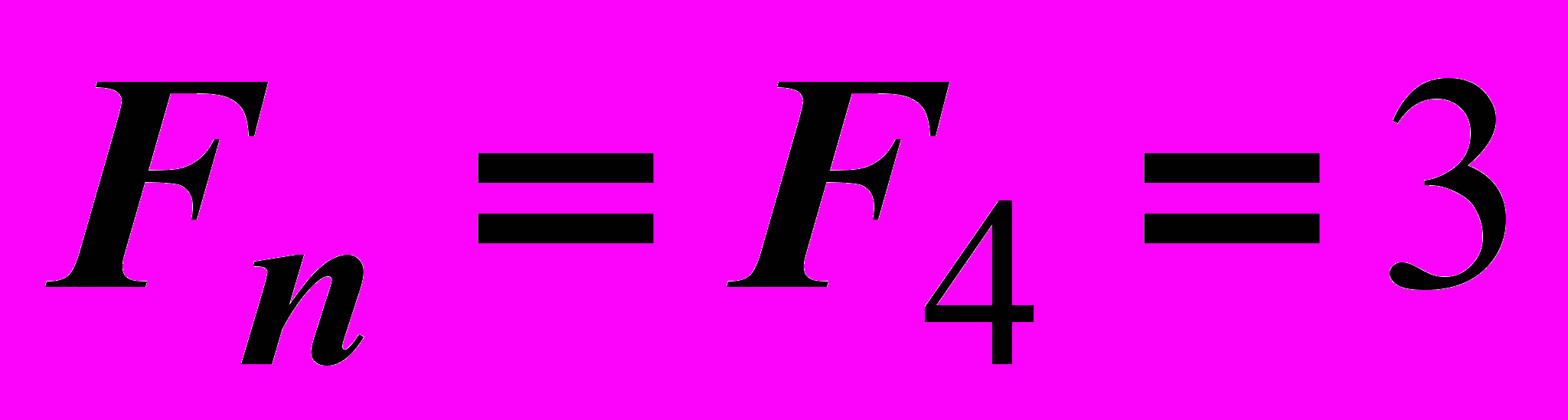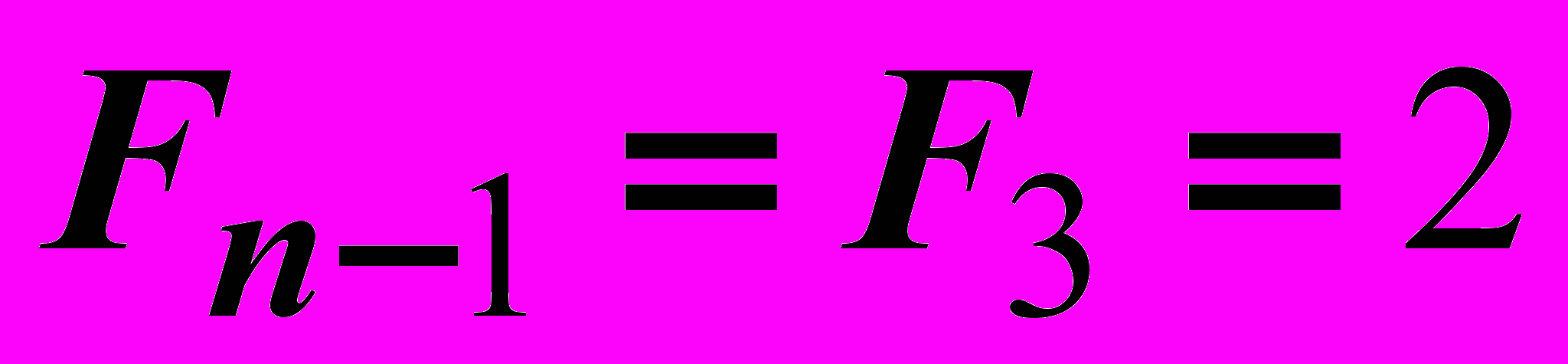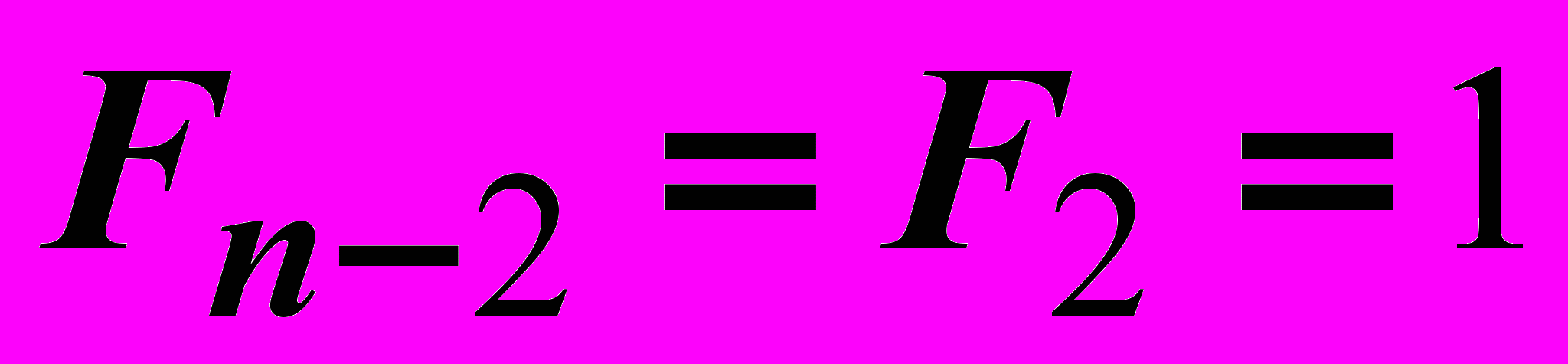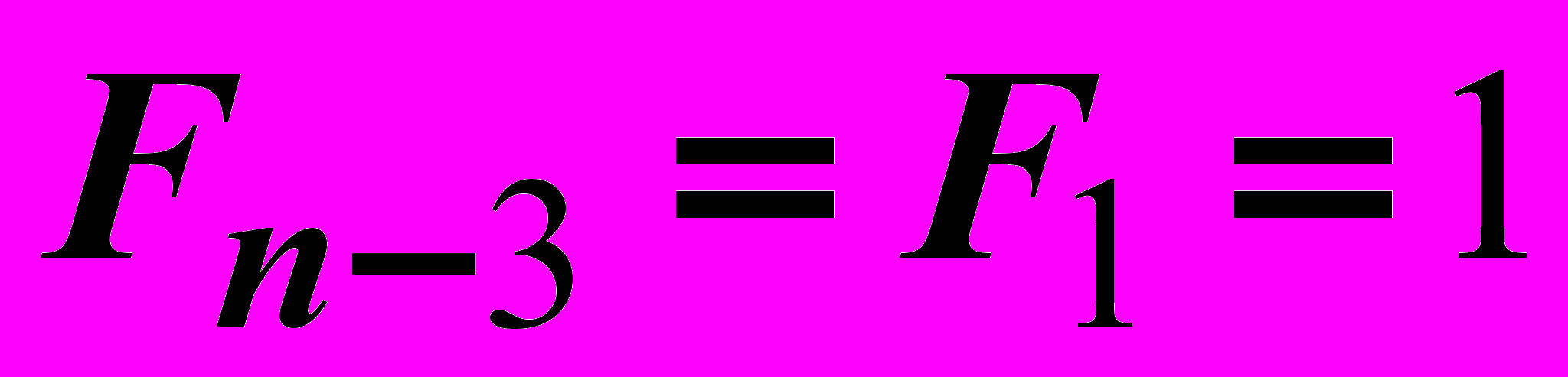.Итерация 1.
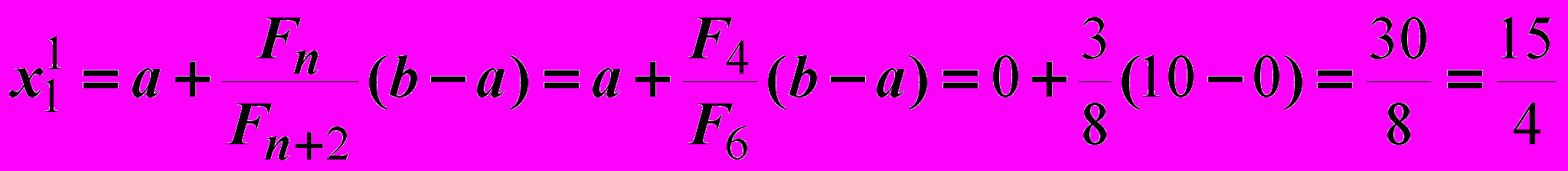
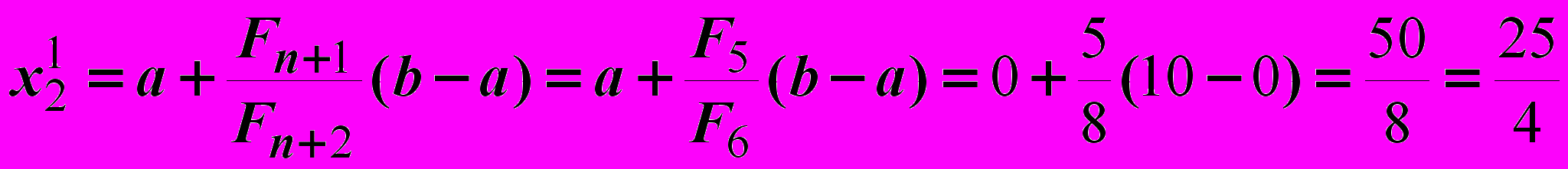
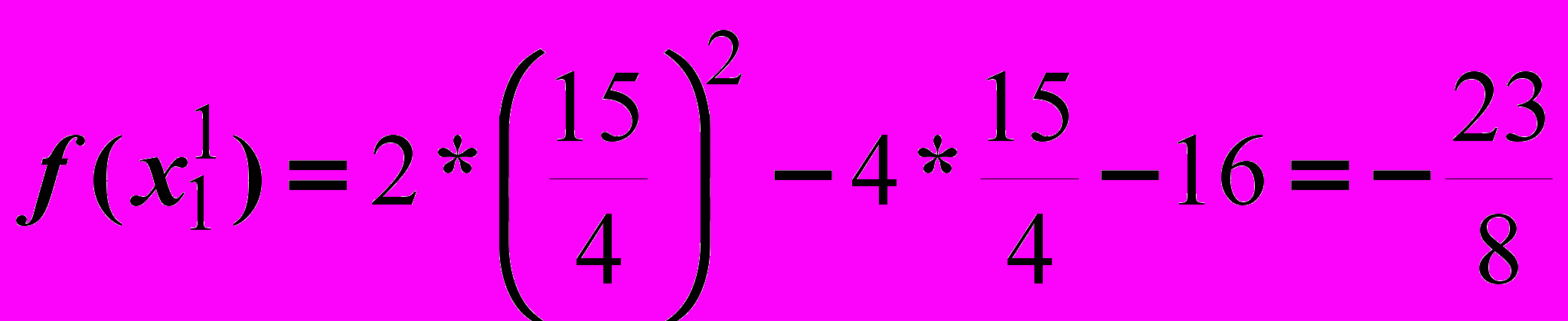
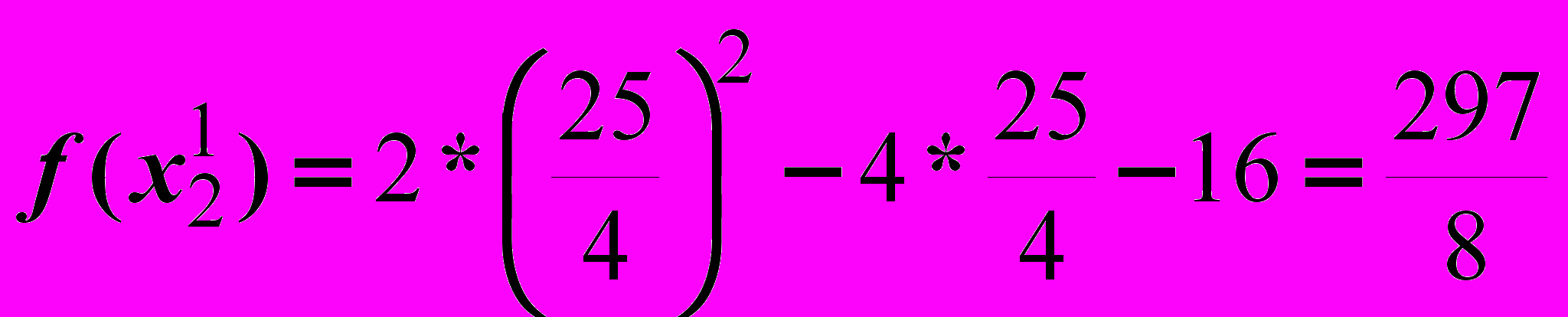
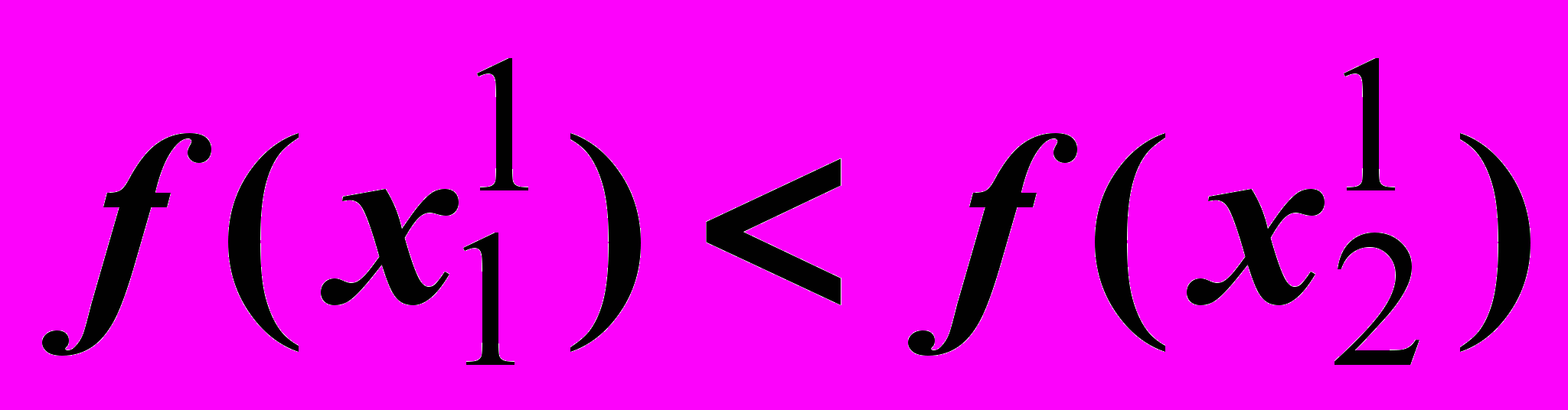
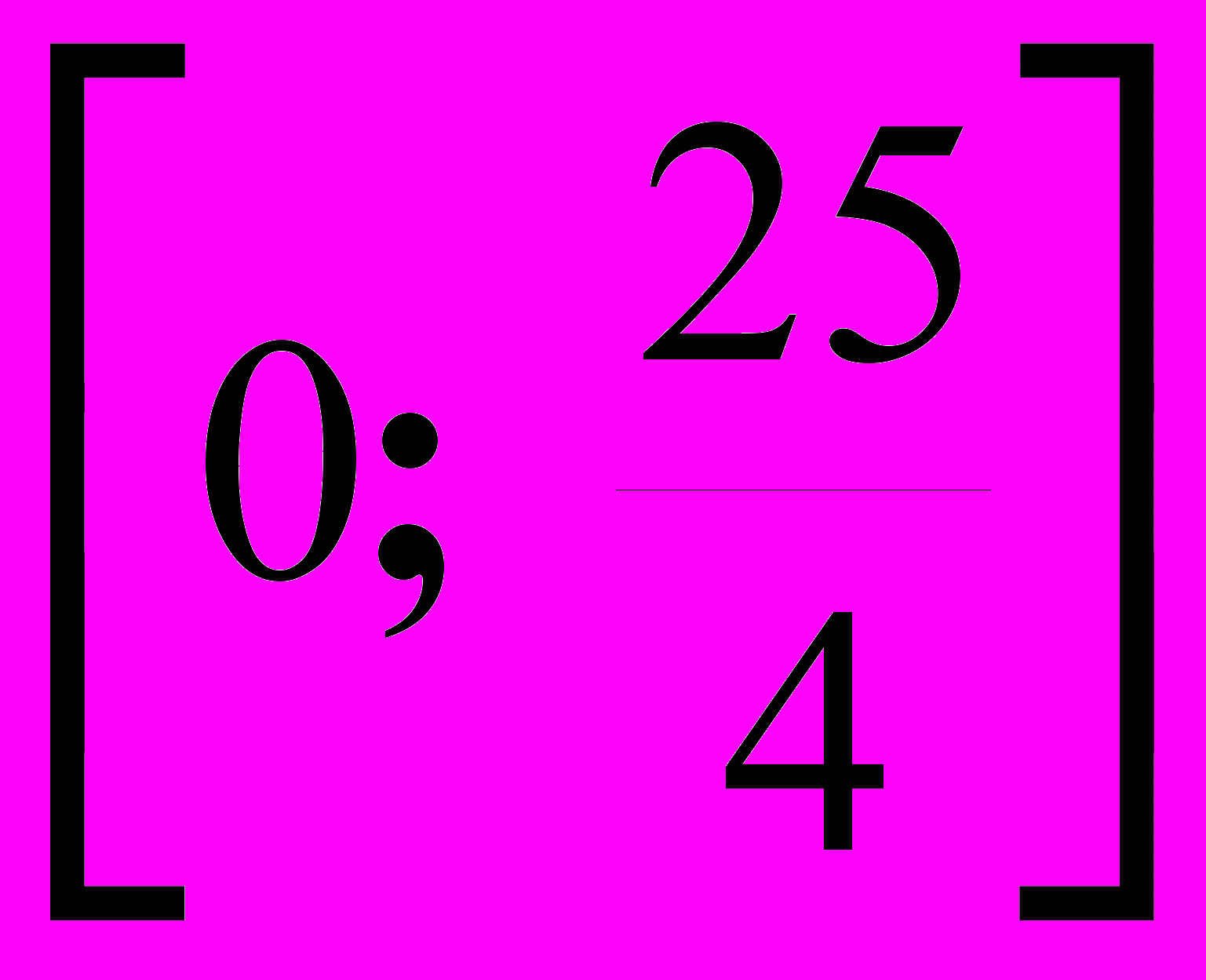
Итерация 2.
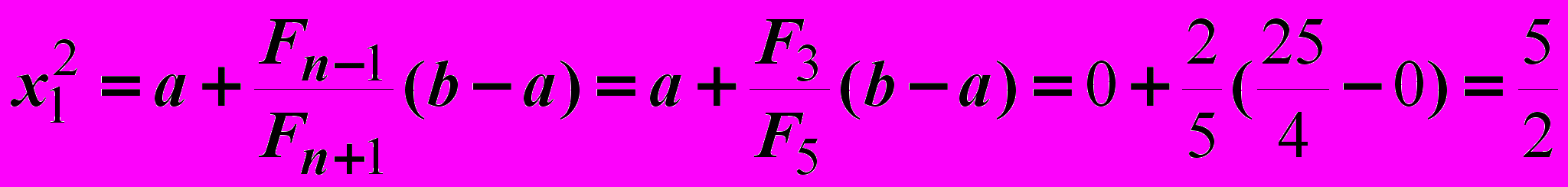
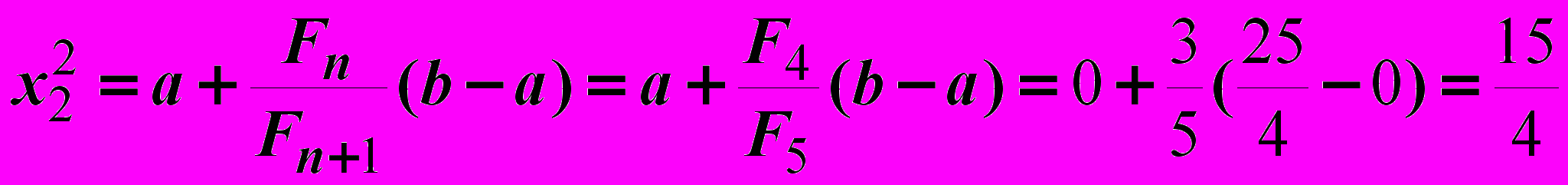
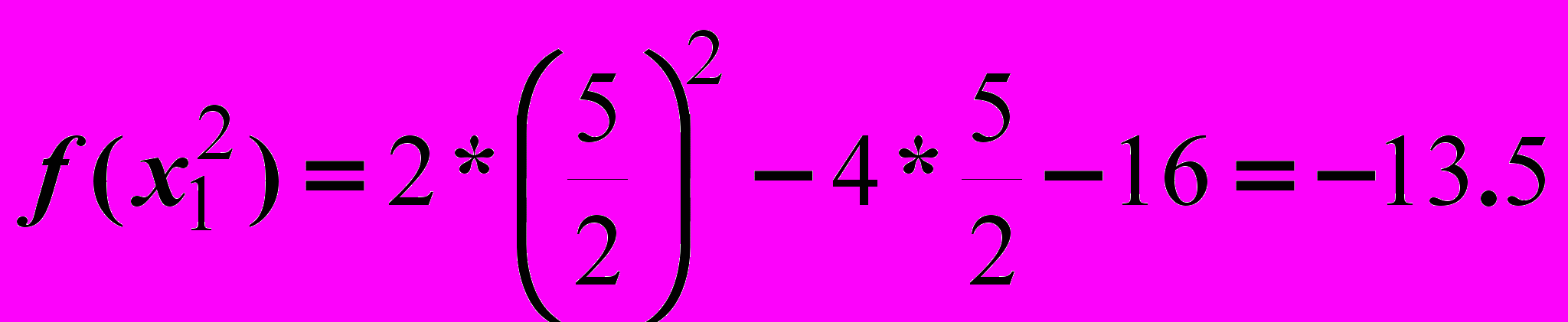
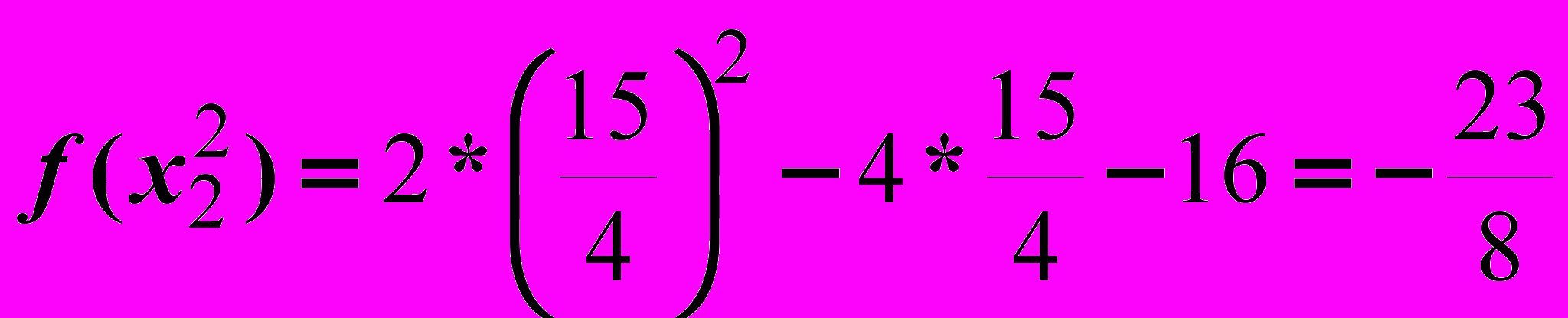
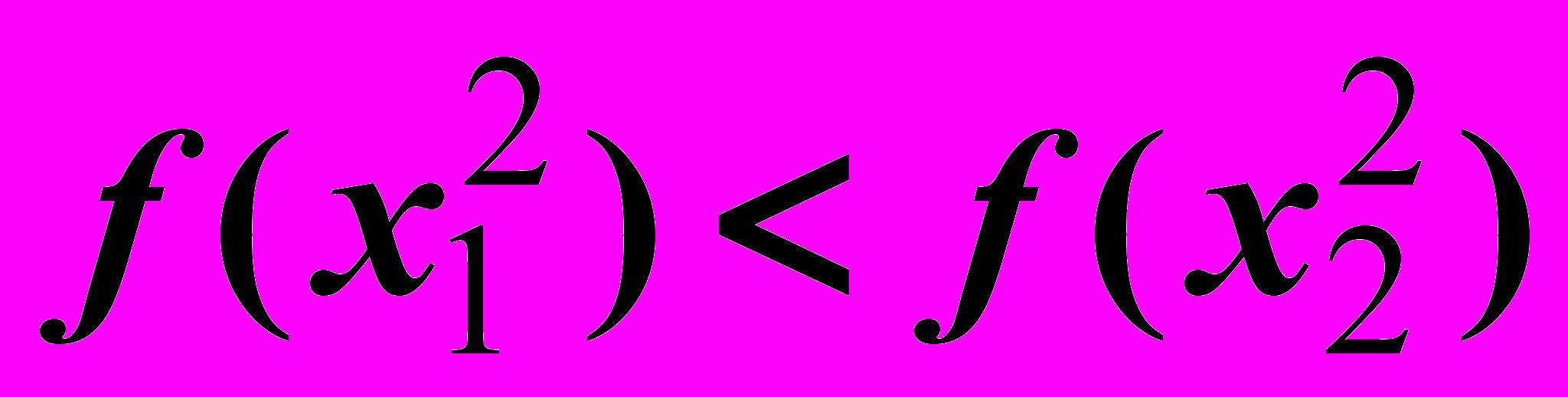
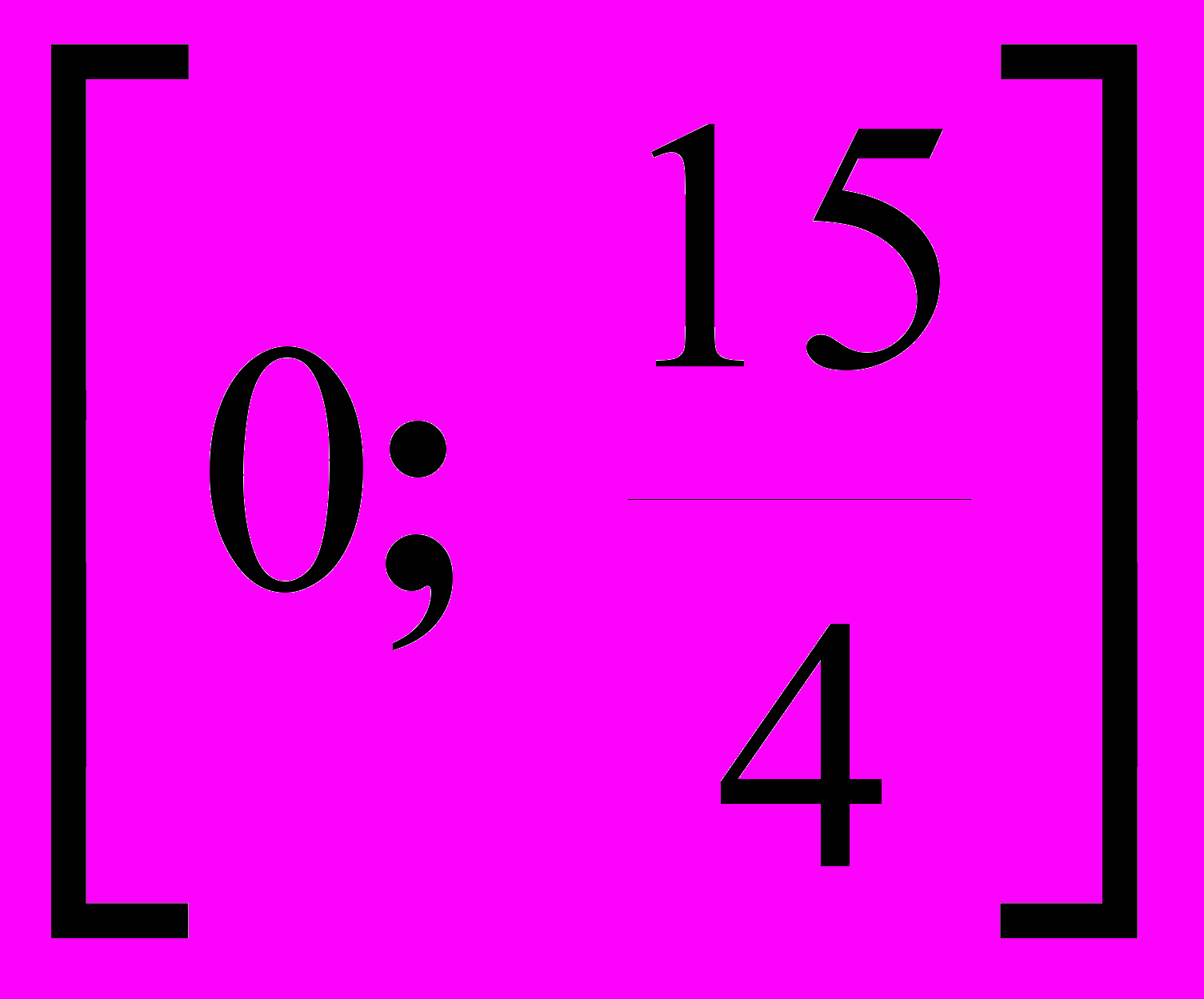
Итерация 3.
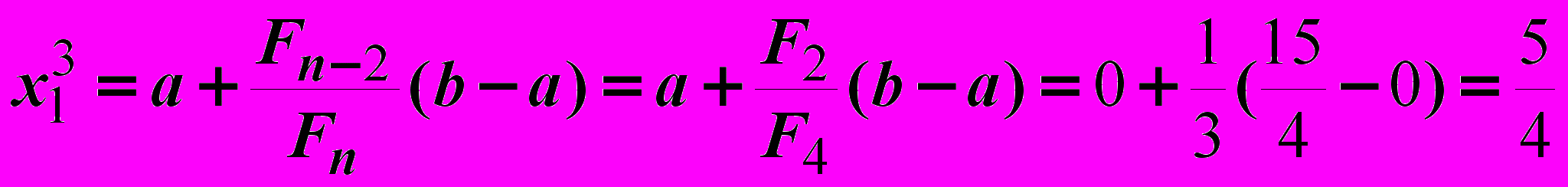
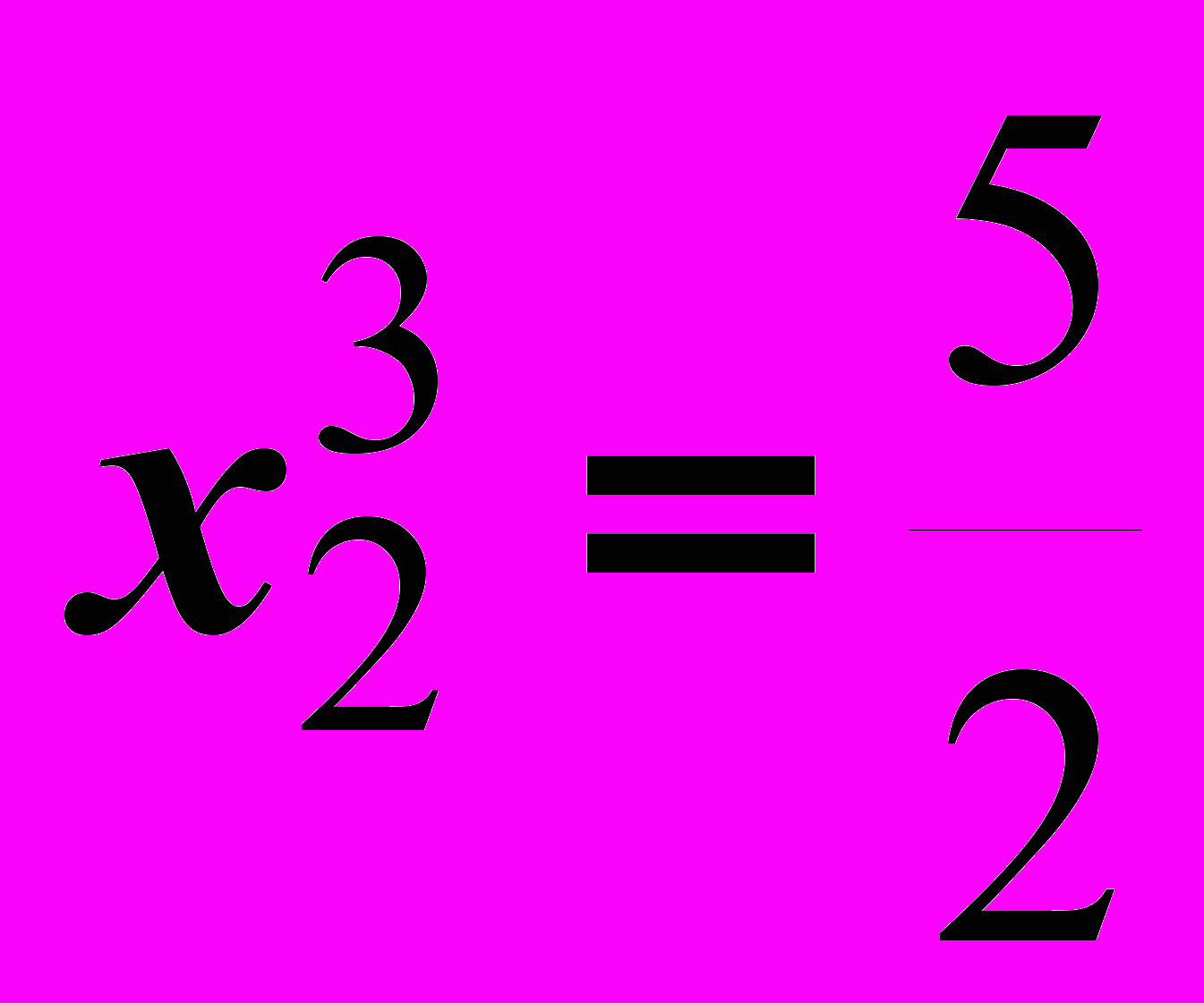
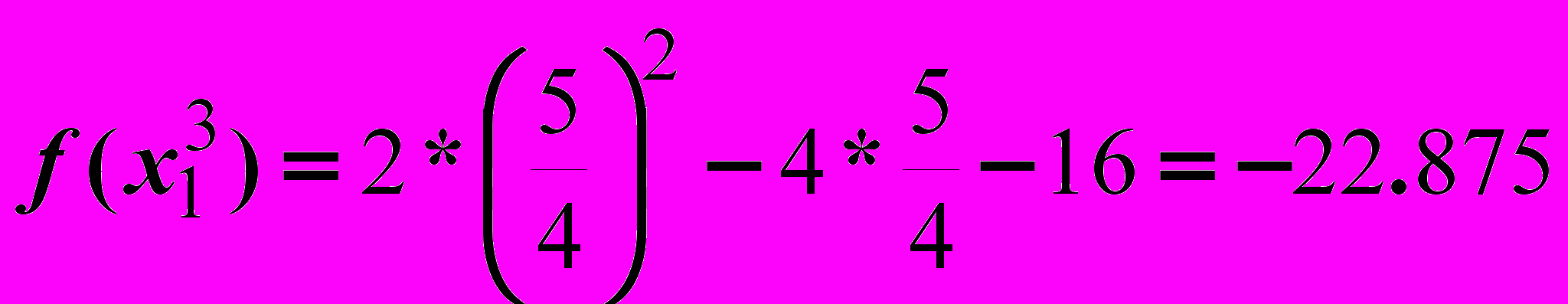
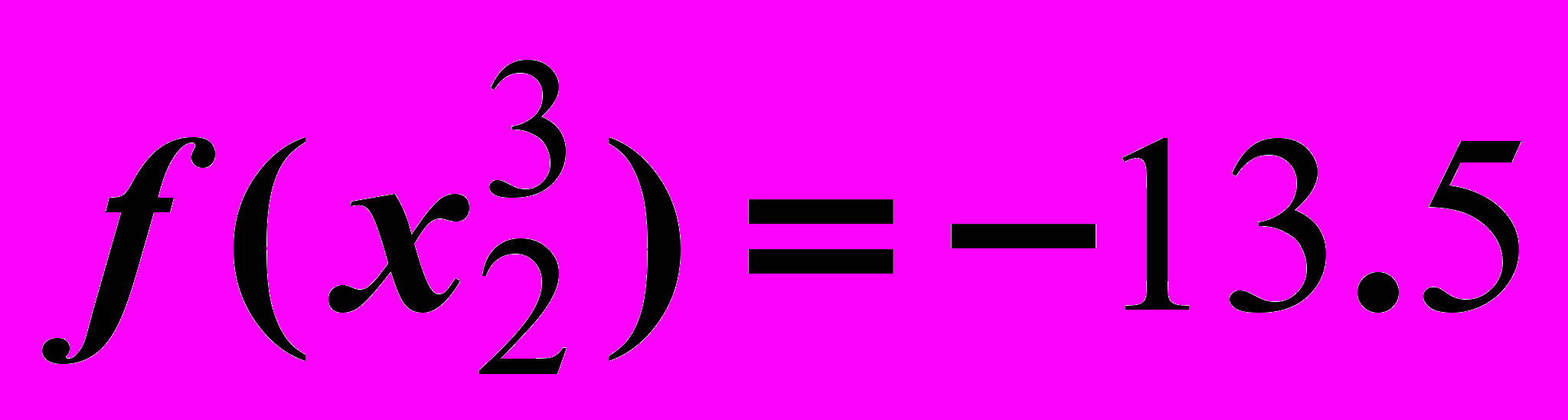
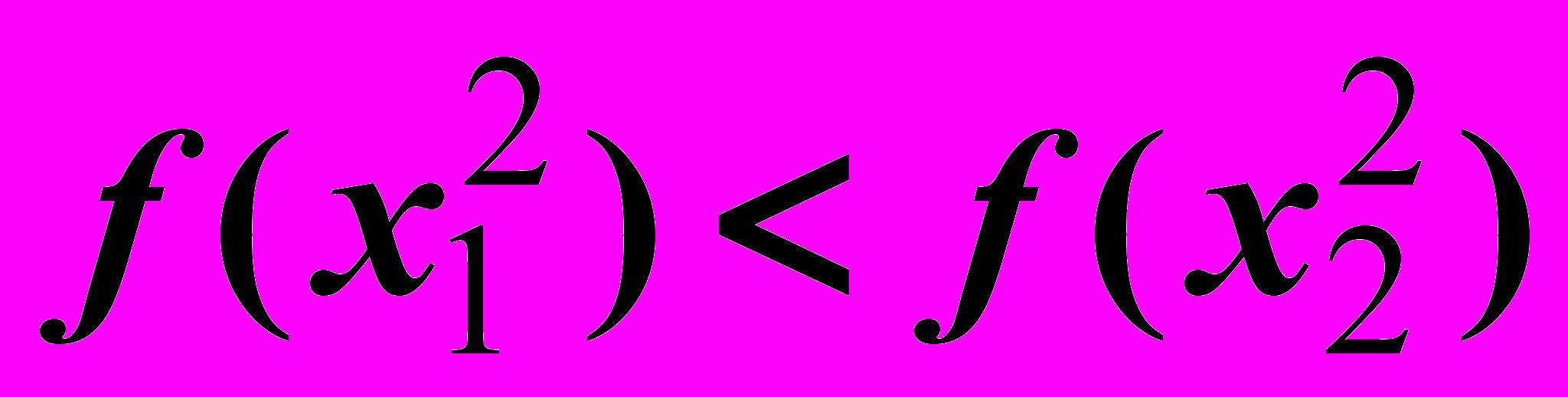
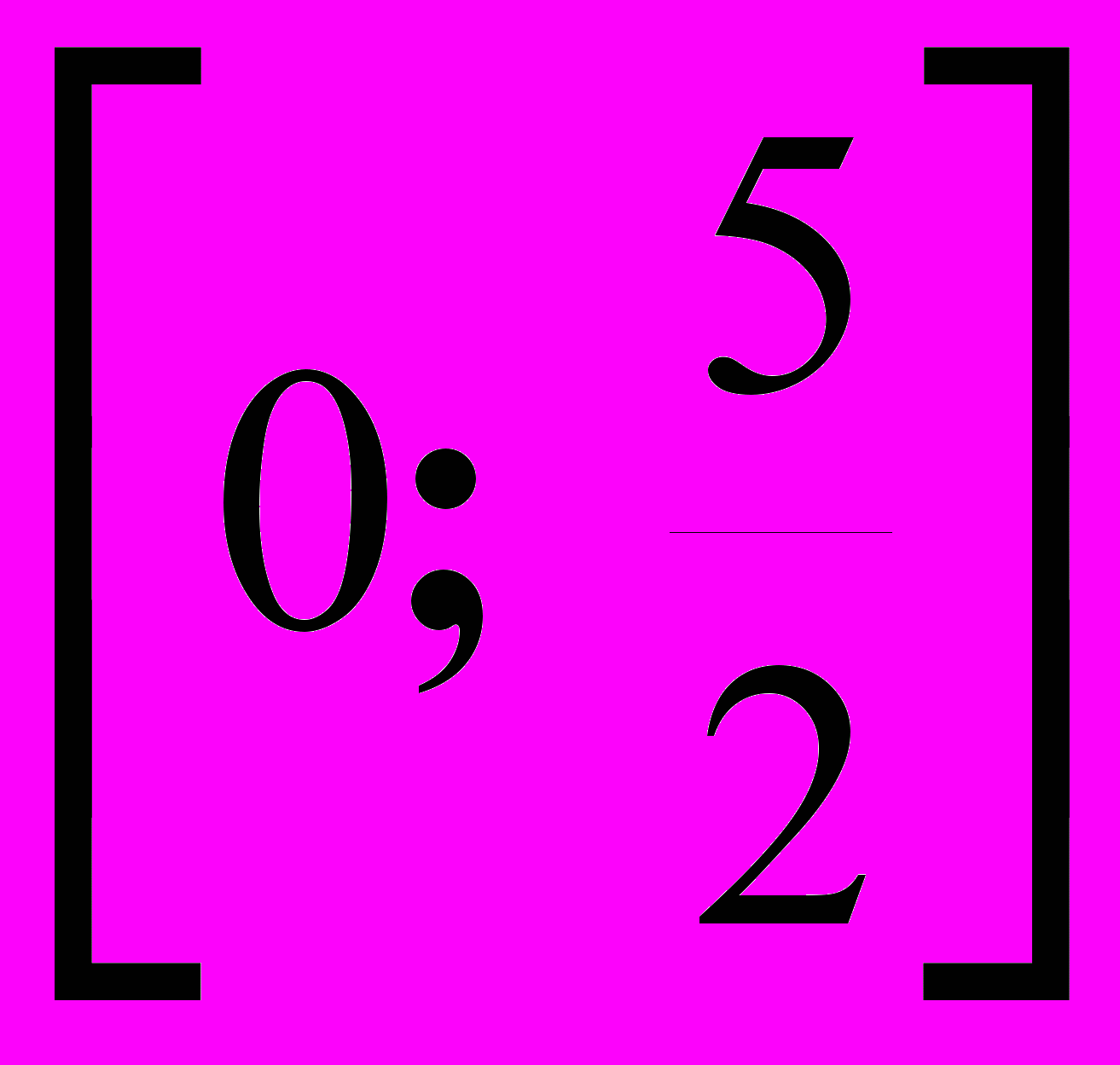
Итерация 4.
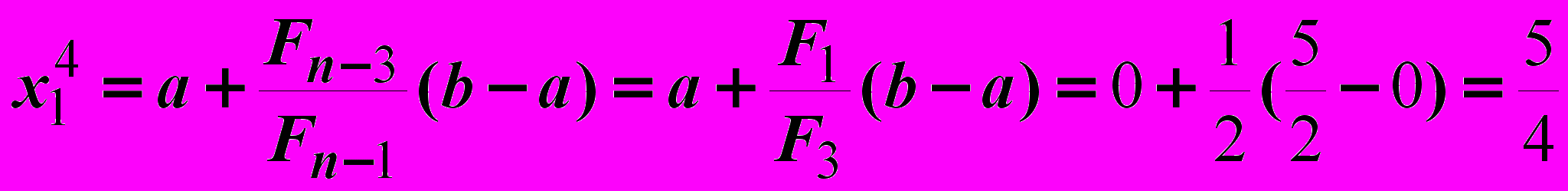
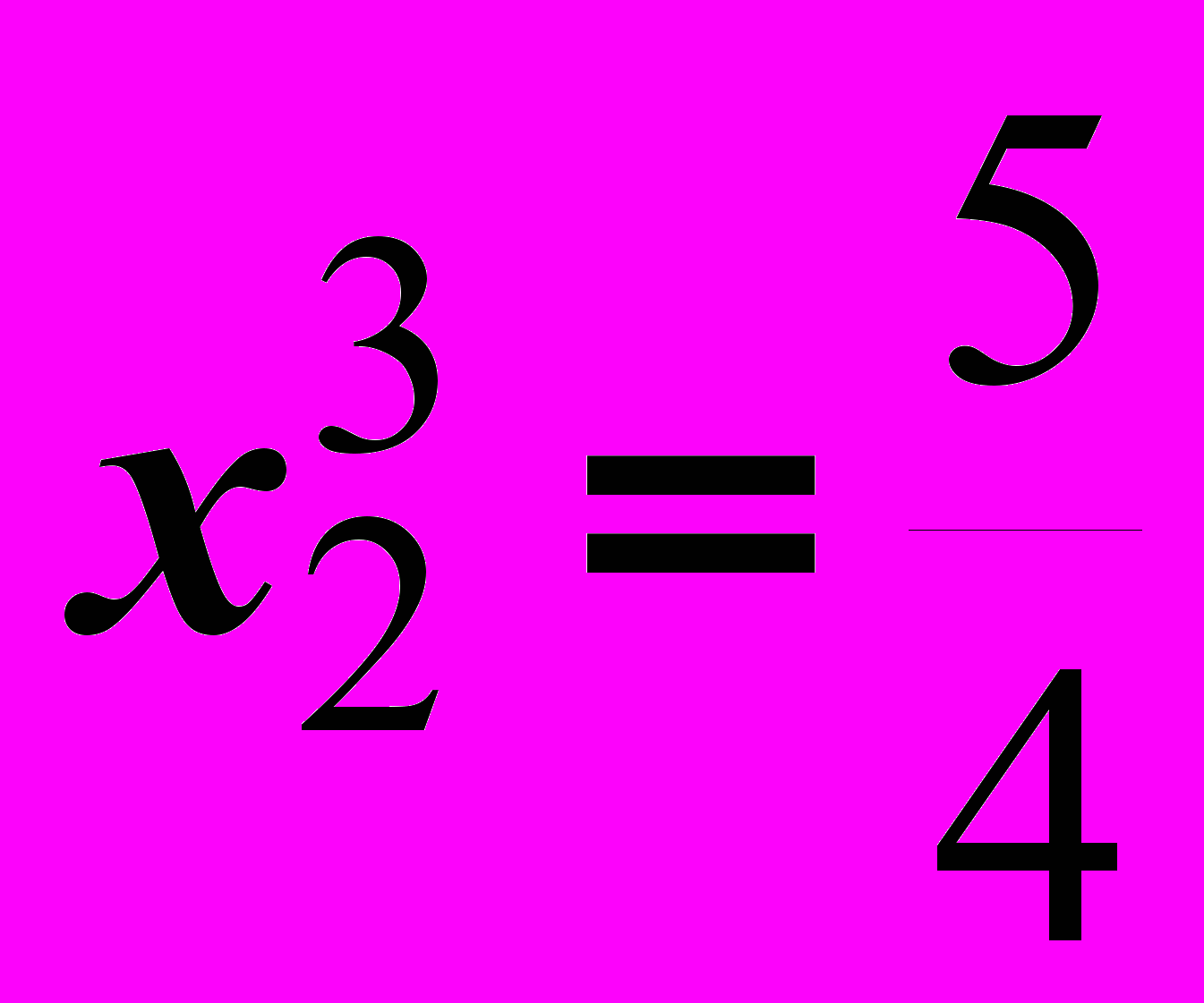
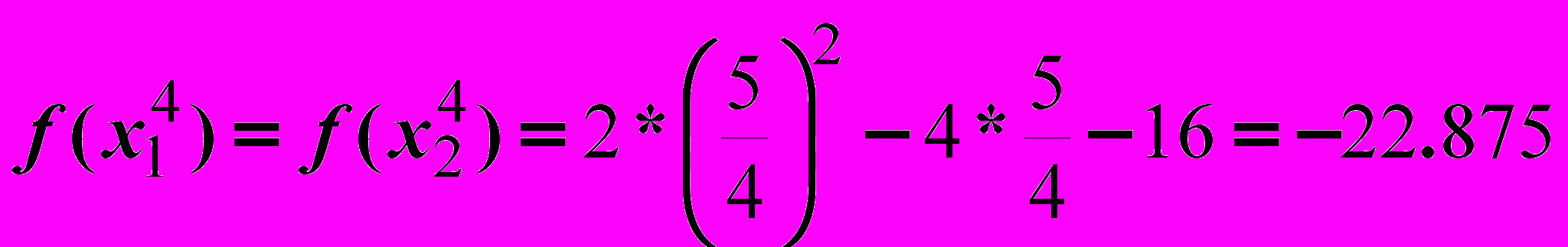
Это и есть точка минимума.
Метод золотого сечения
Часто, через
обозначают следующее выражение: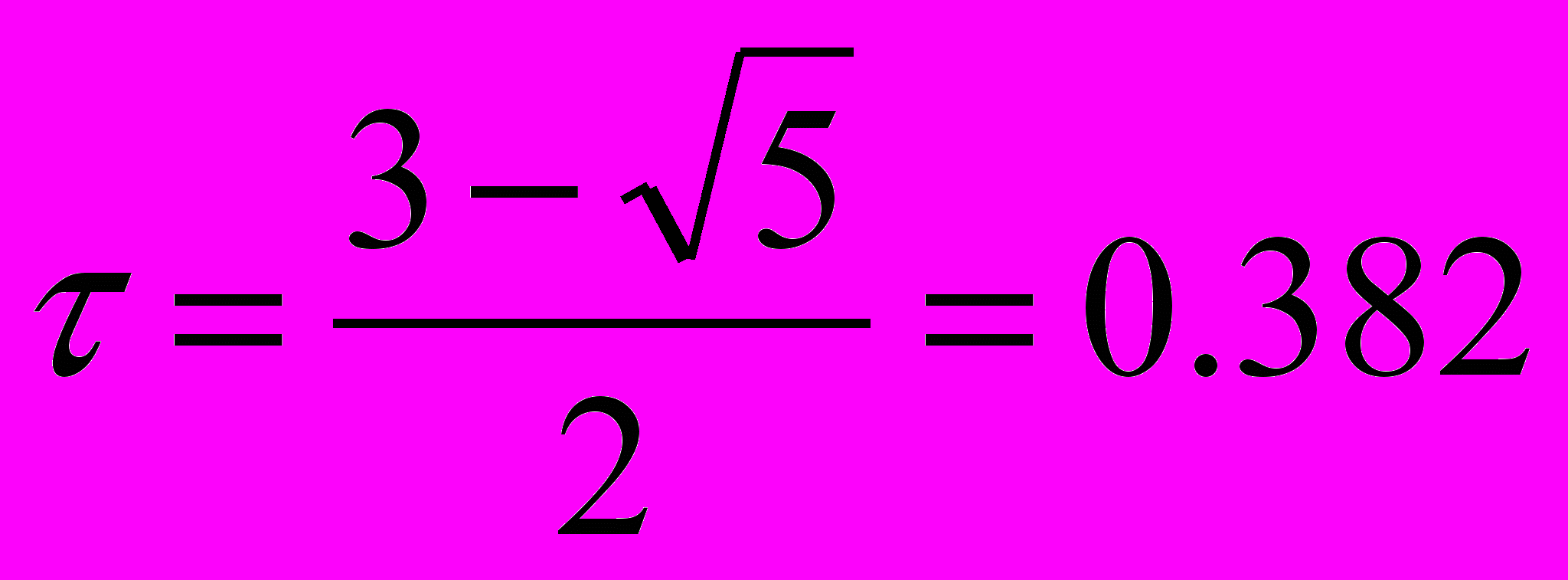
,тогда точка золотого сечения вычисляется по формуле:
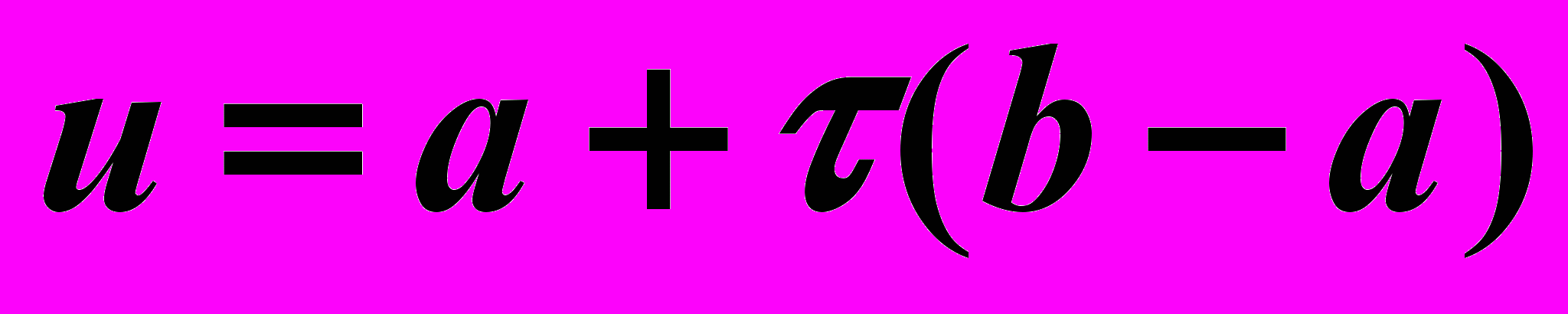
Обозначим точку золотого сечения через
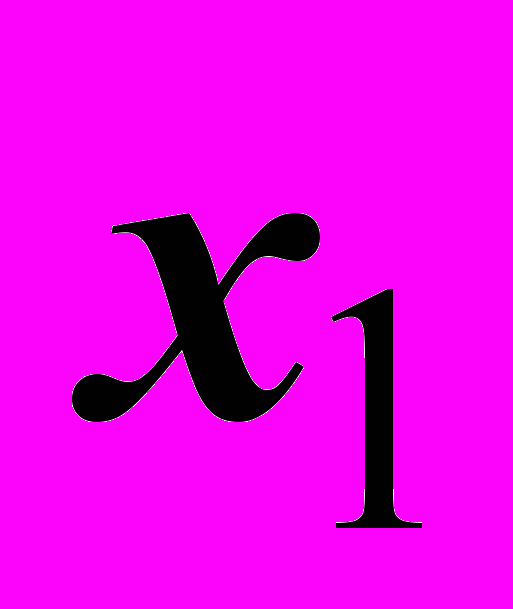, тогда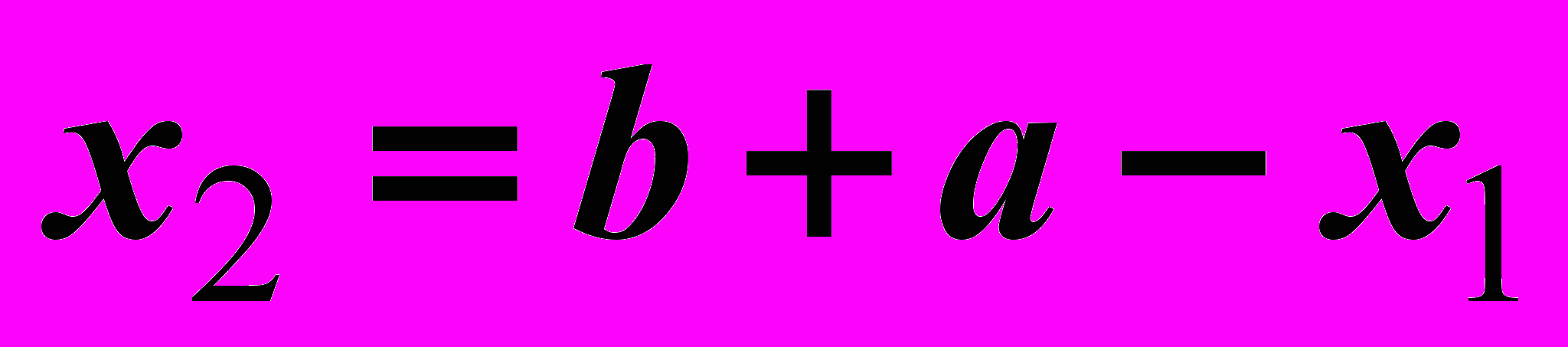 
Пример. Найти минимум функции f(x)=(100-x)2 в интервале 60 x 150. Методом золотого сечения.
Здесь a=60, b=150 и L=150-60=90, L1=12.
Итерация 1.
=> 
=> 
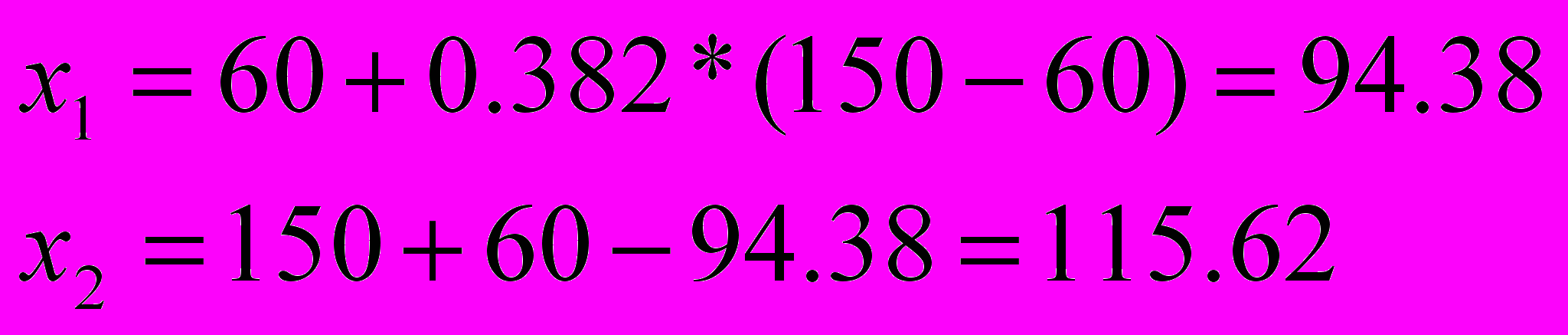
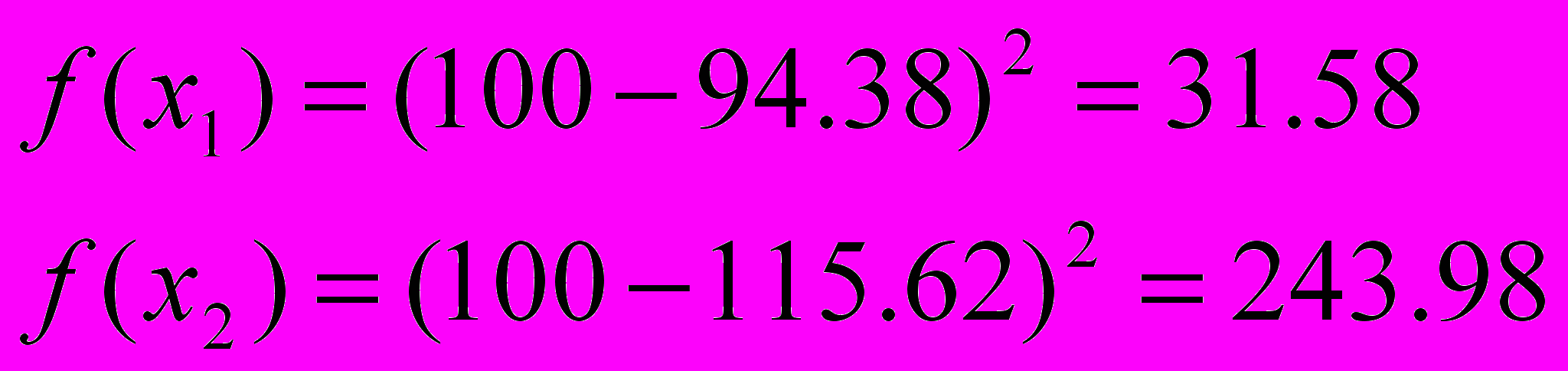
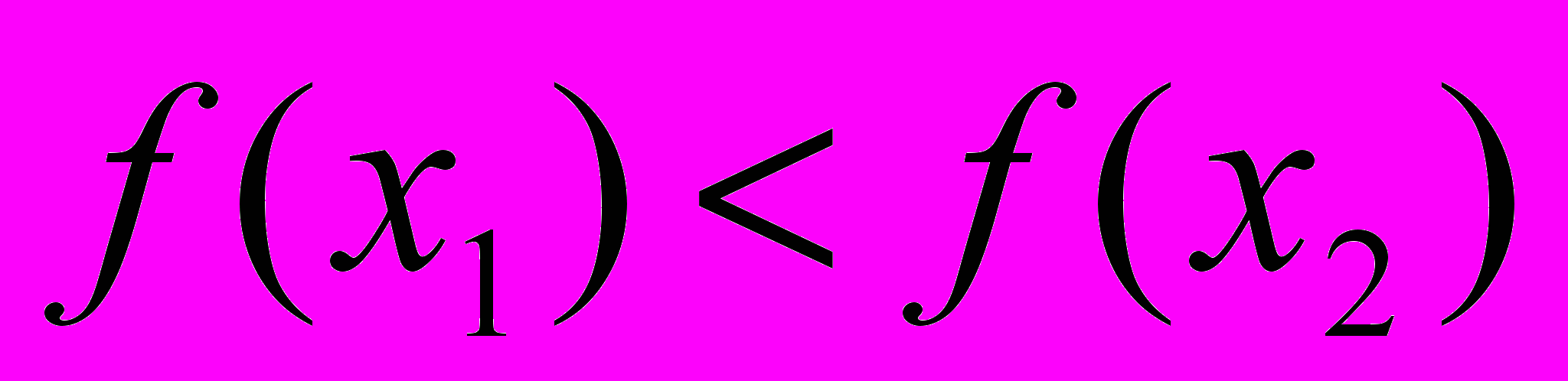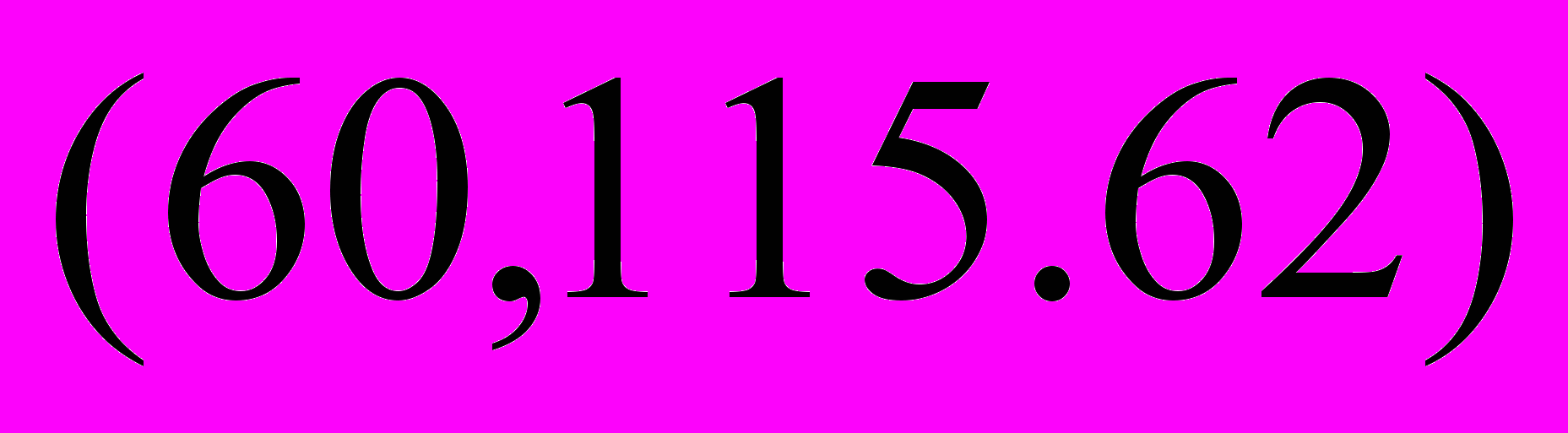
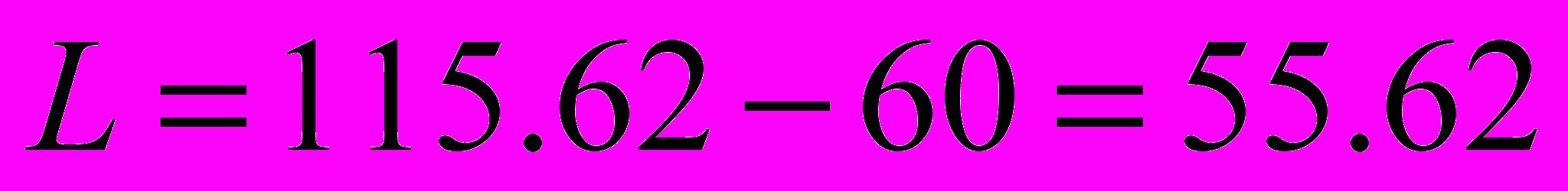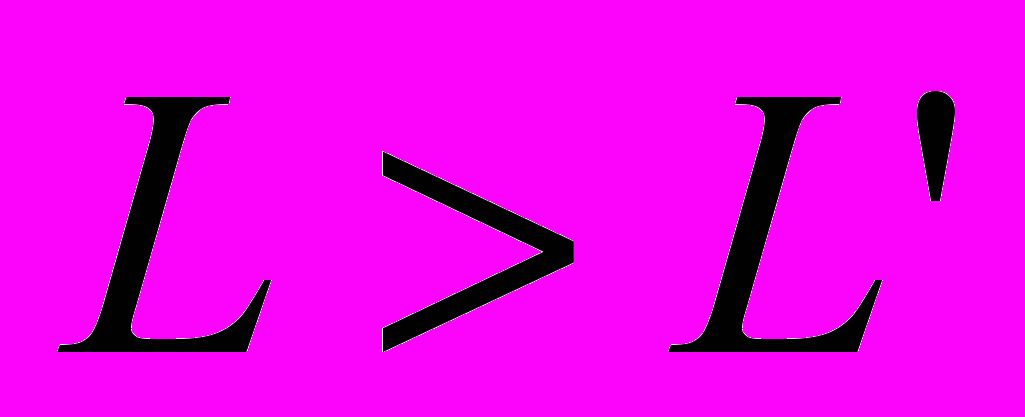
Итерация 2.
, 
=> 
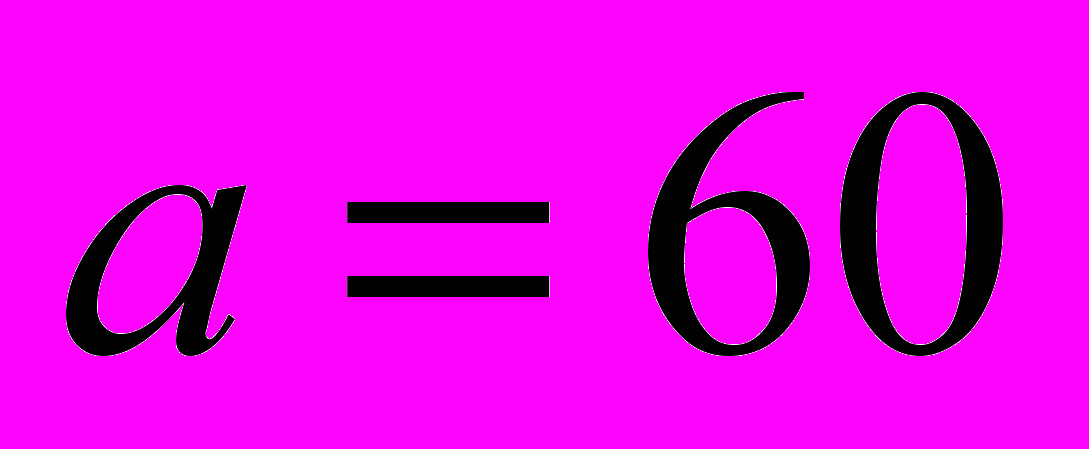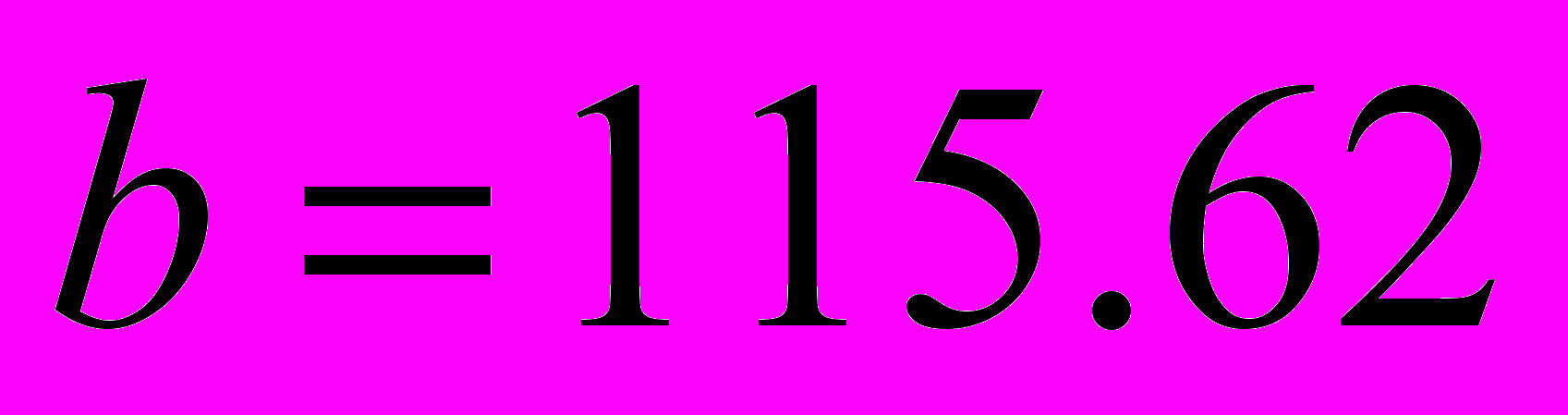
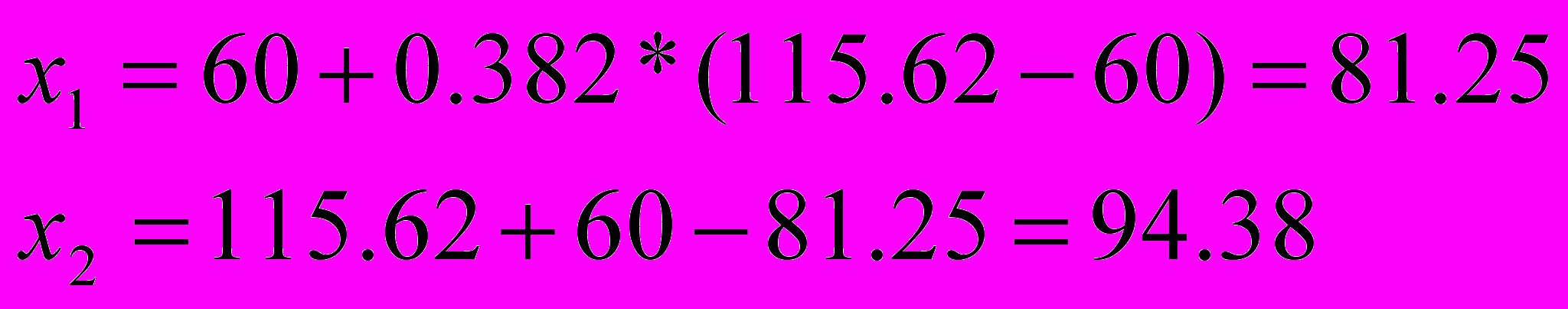
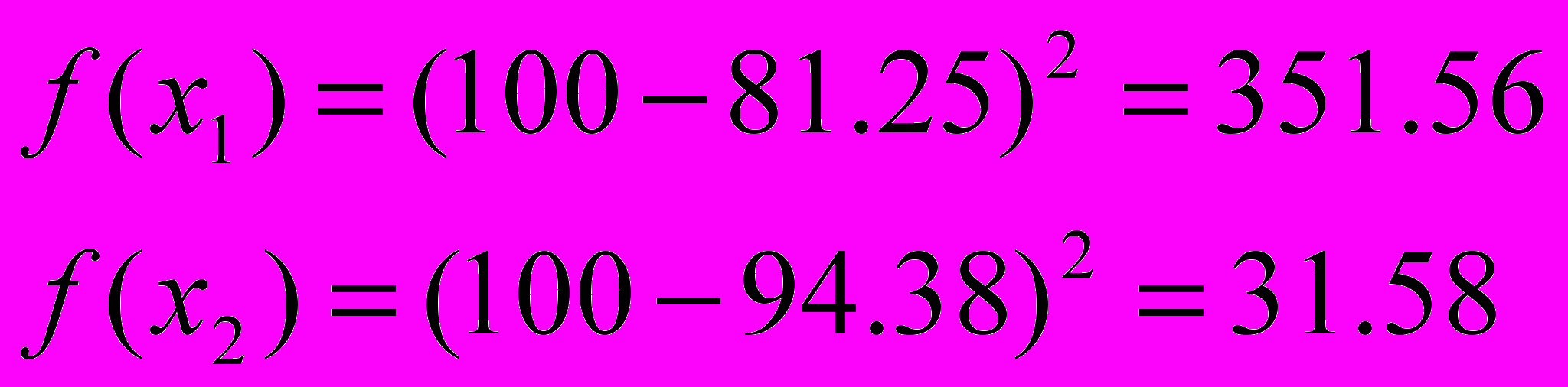
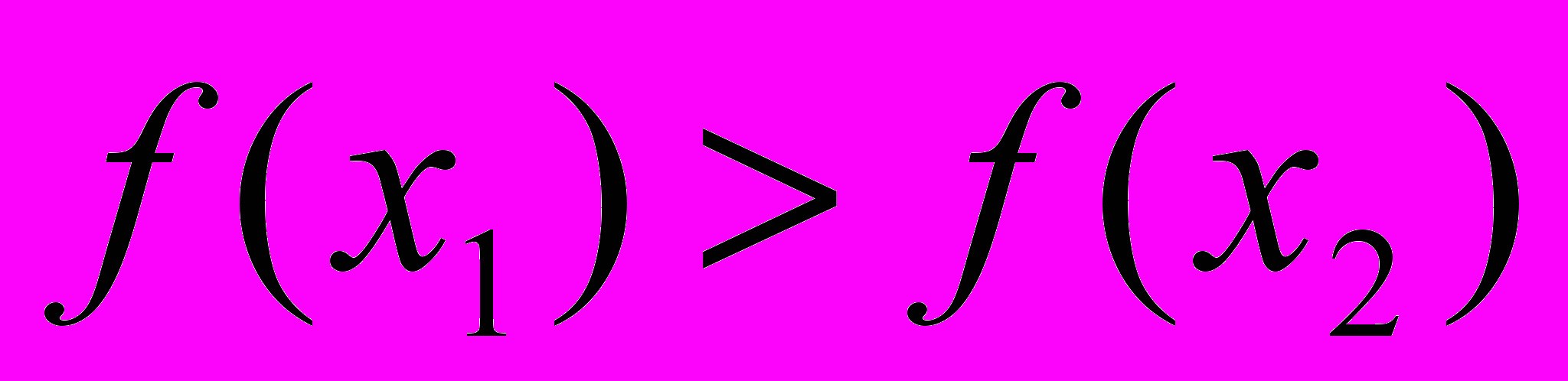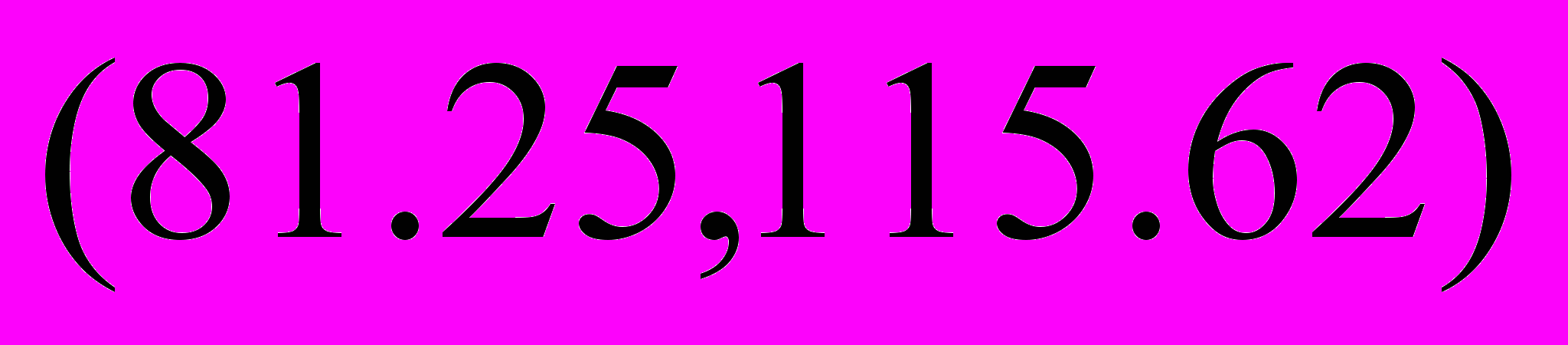
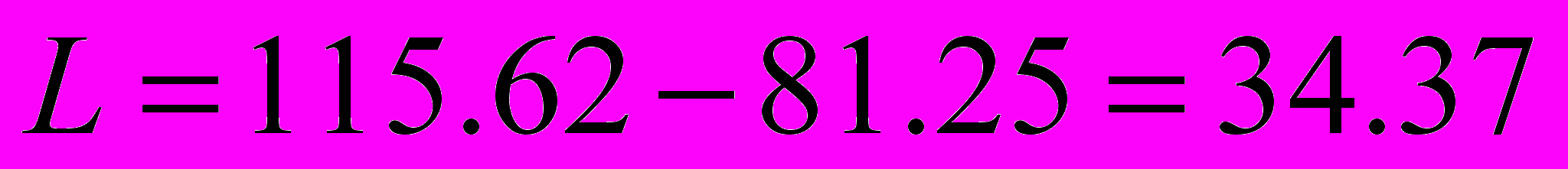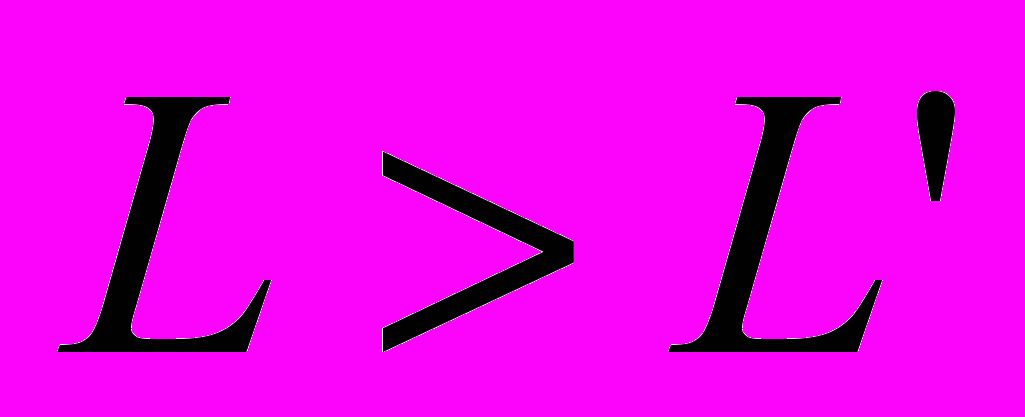
=> Итерация 3.
, 
=> 
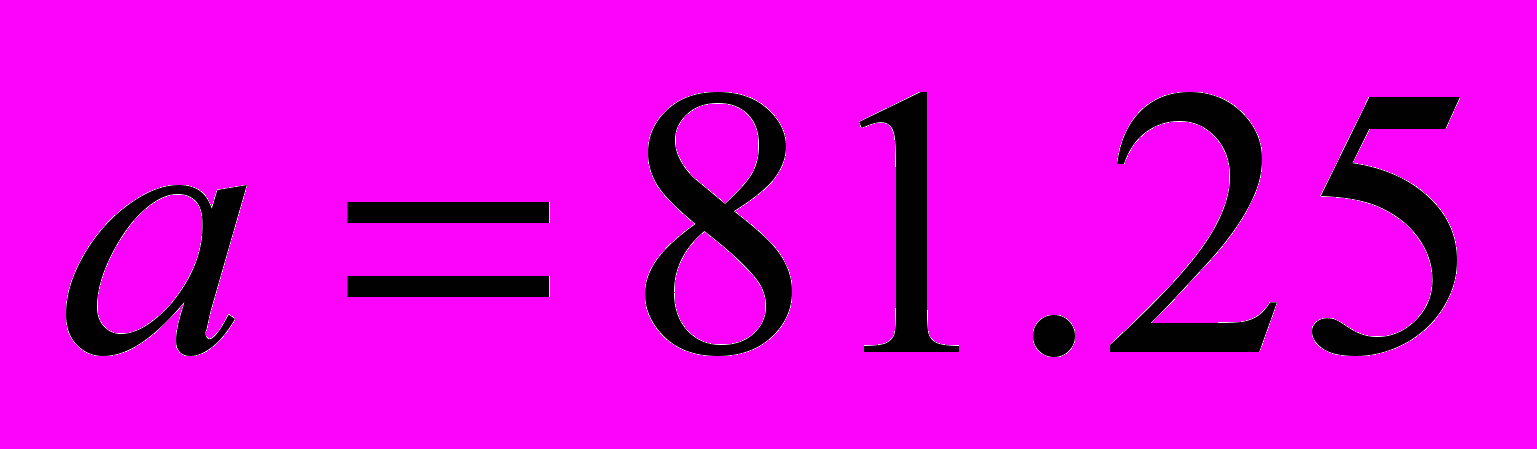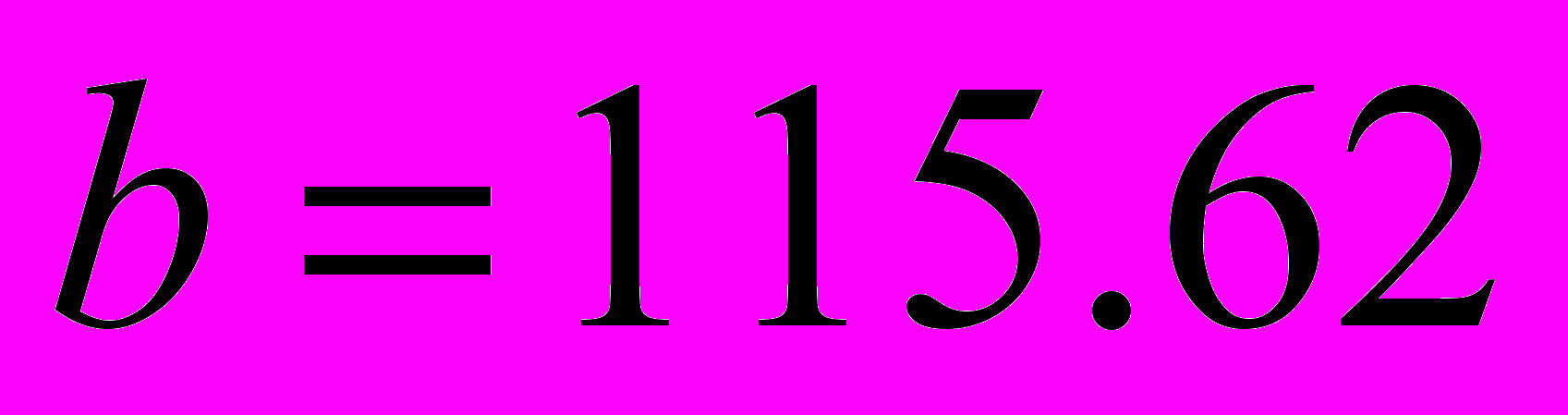
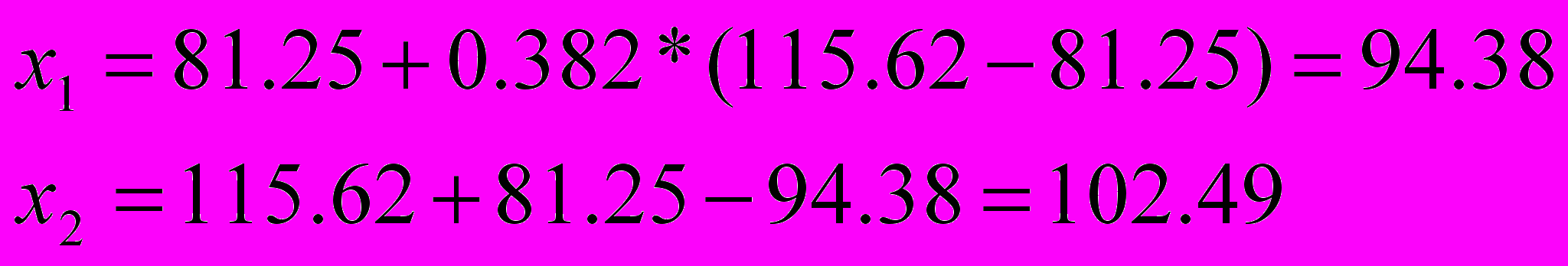
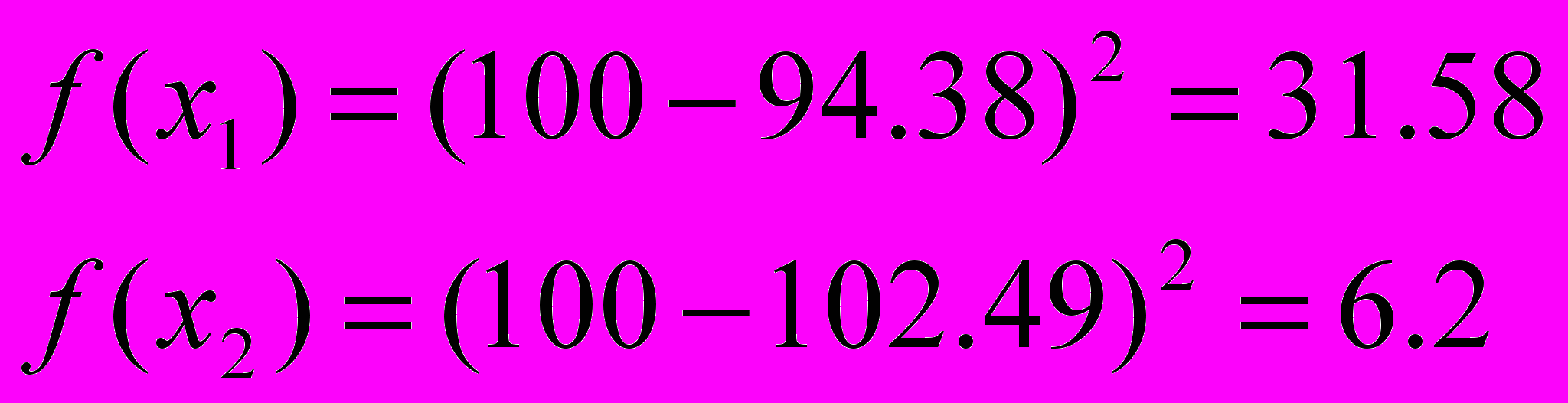
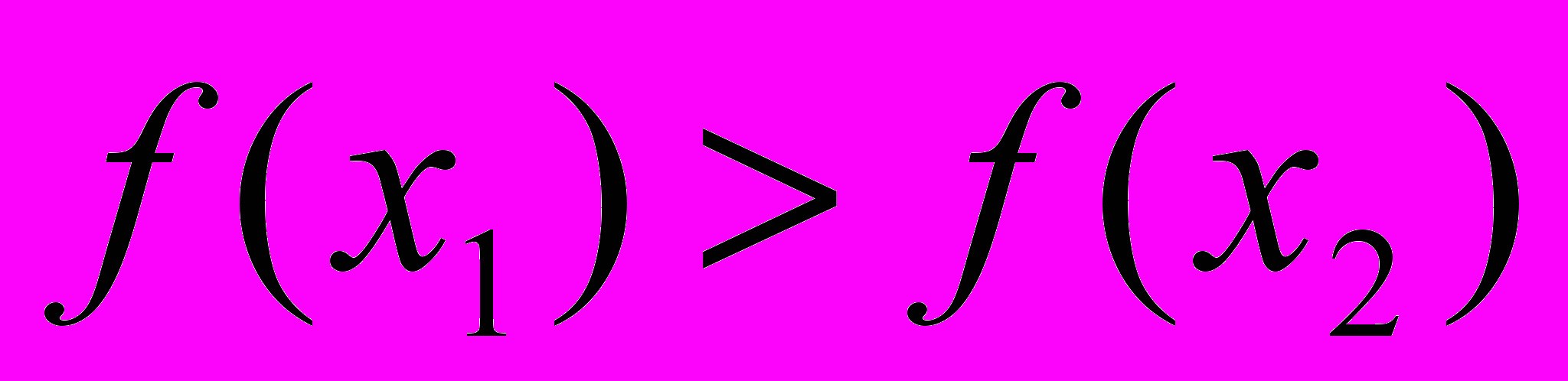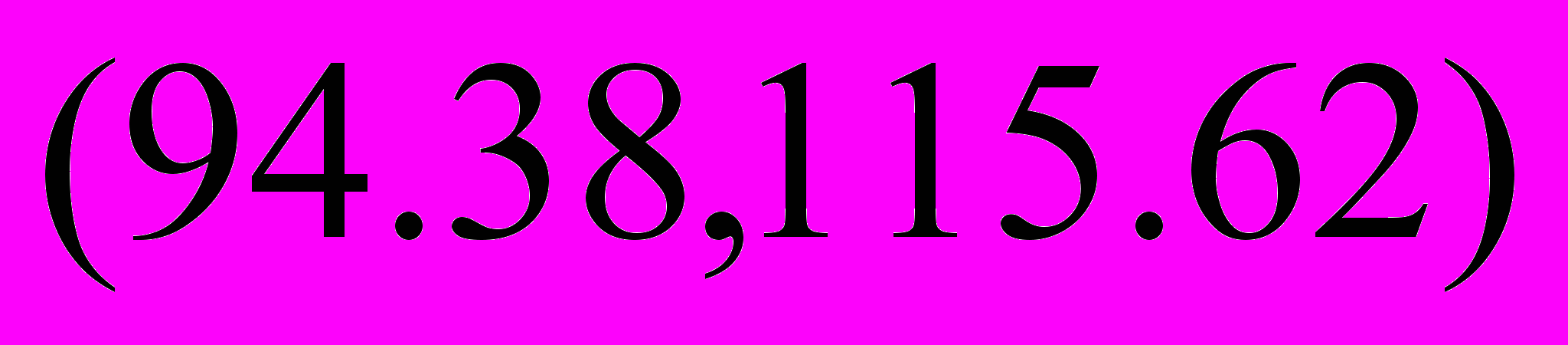
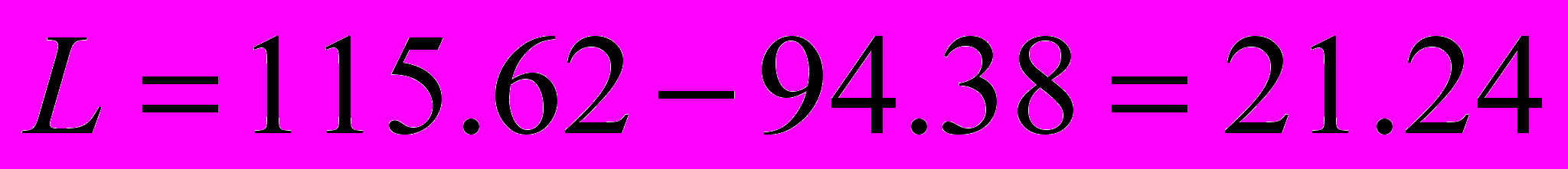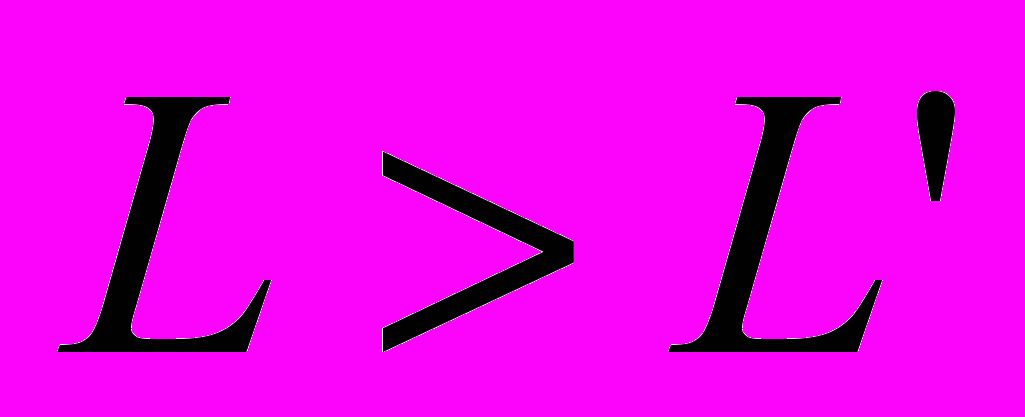
=> Итерация 4.
, 
=> 
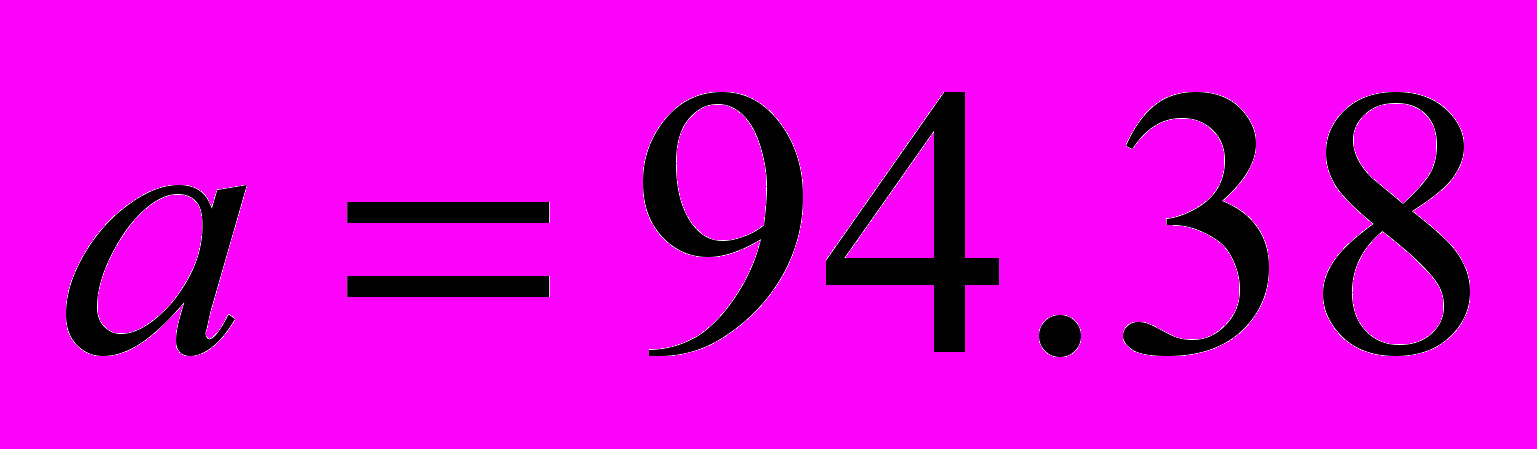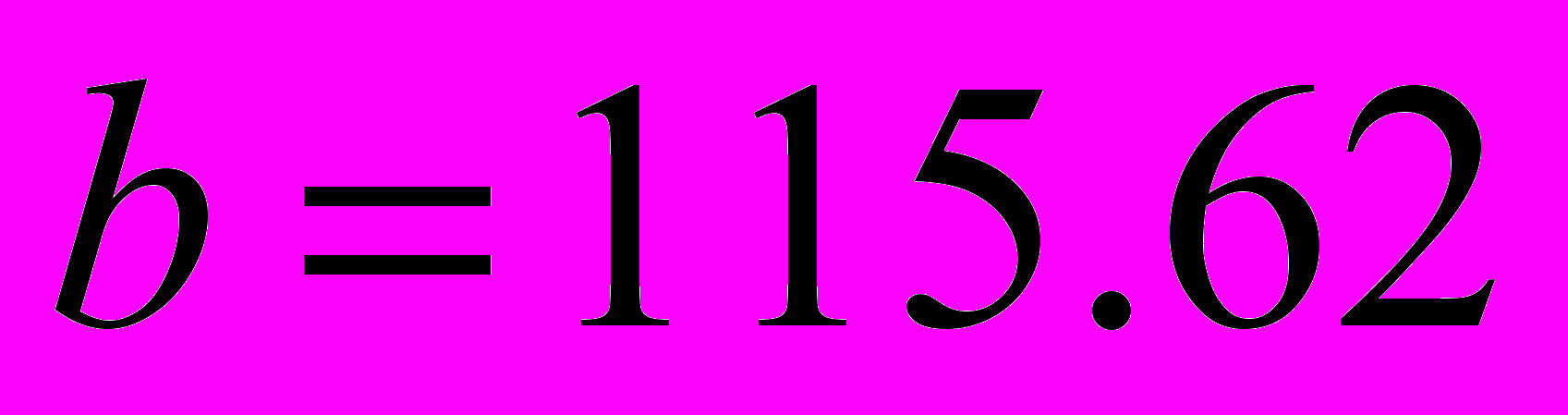
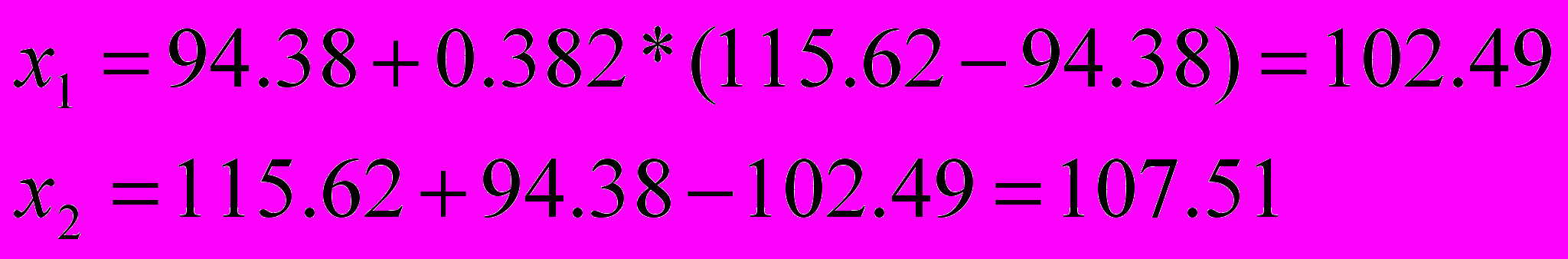
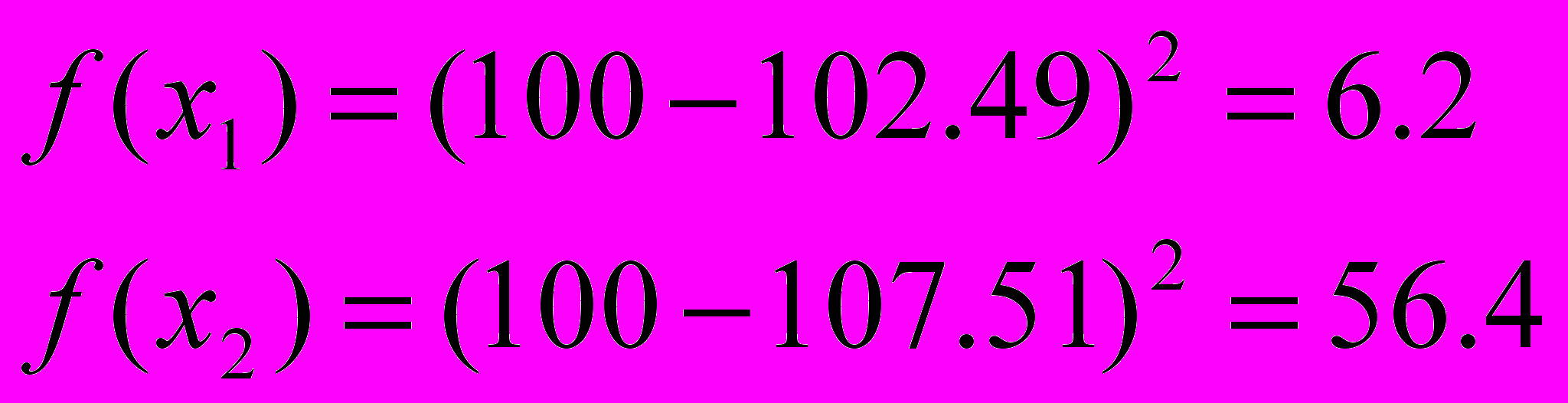
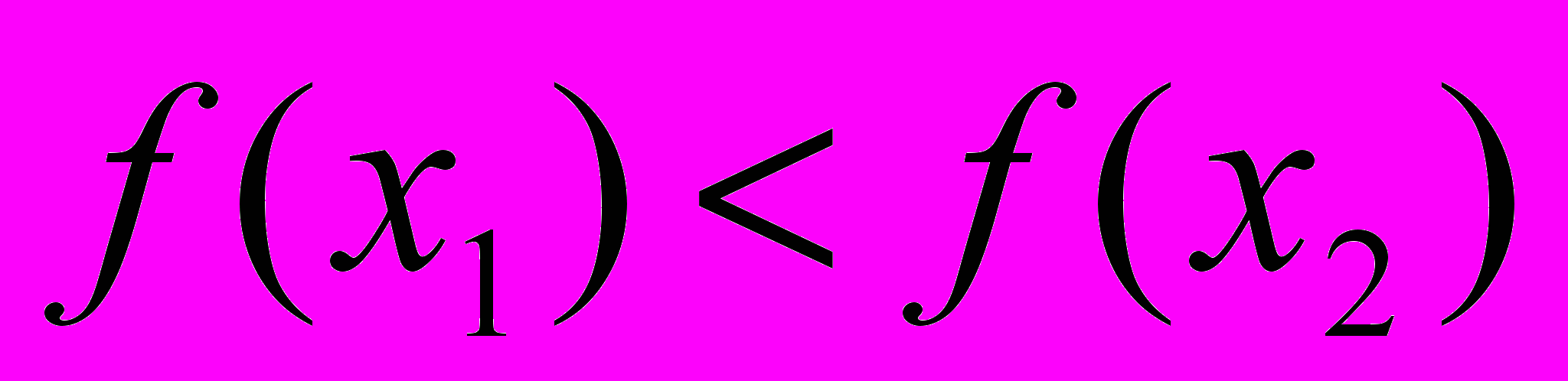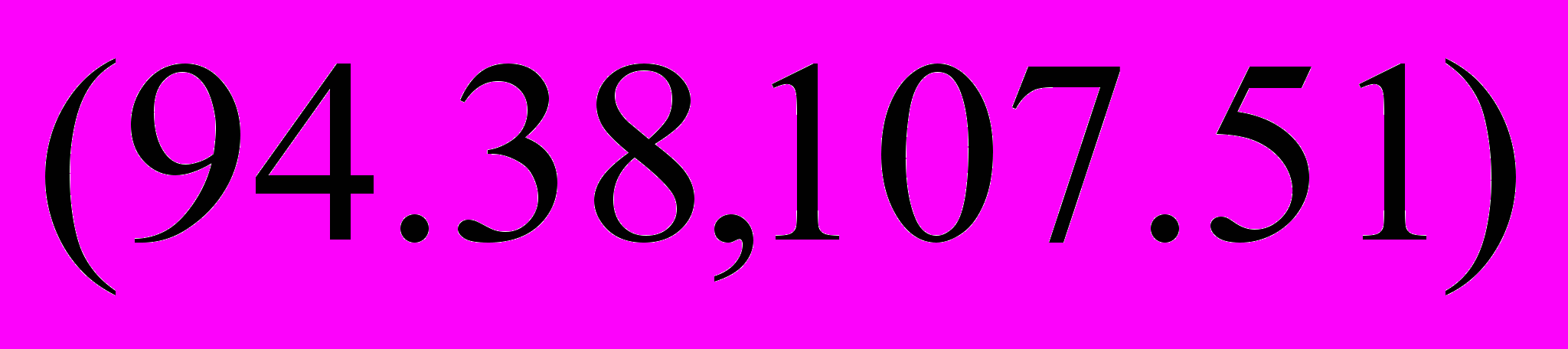
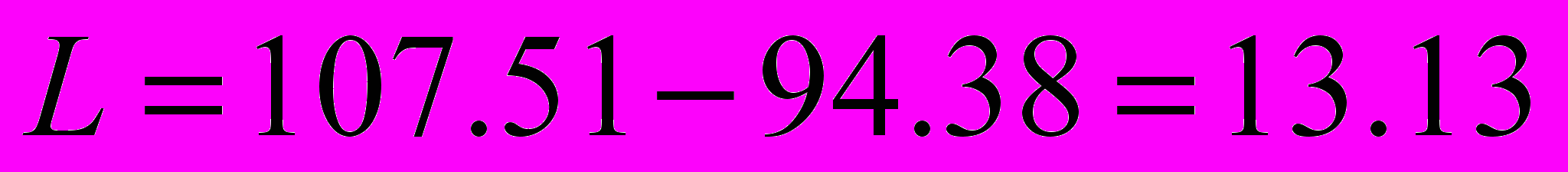=> Итерация 5.
, 
=> 
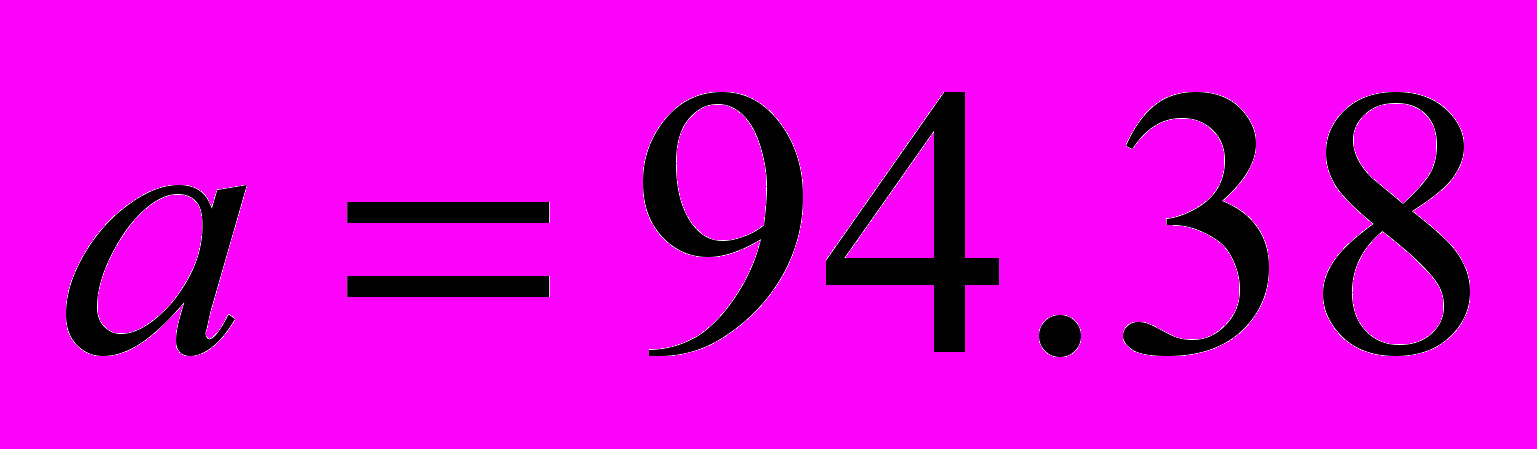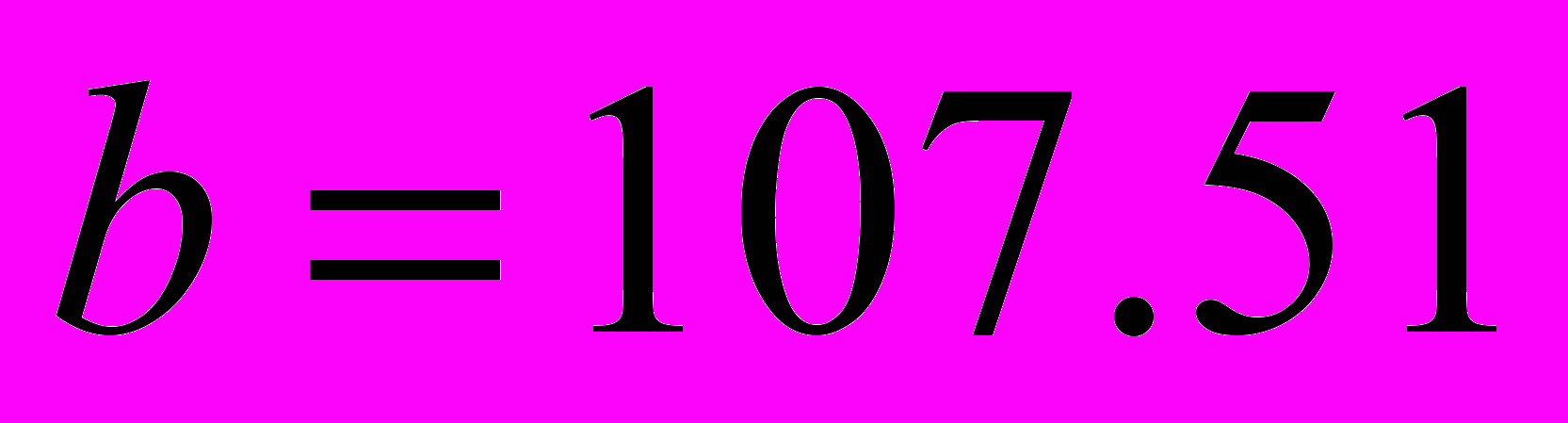
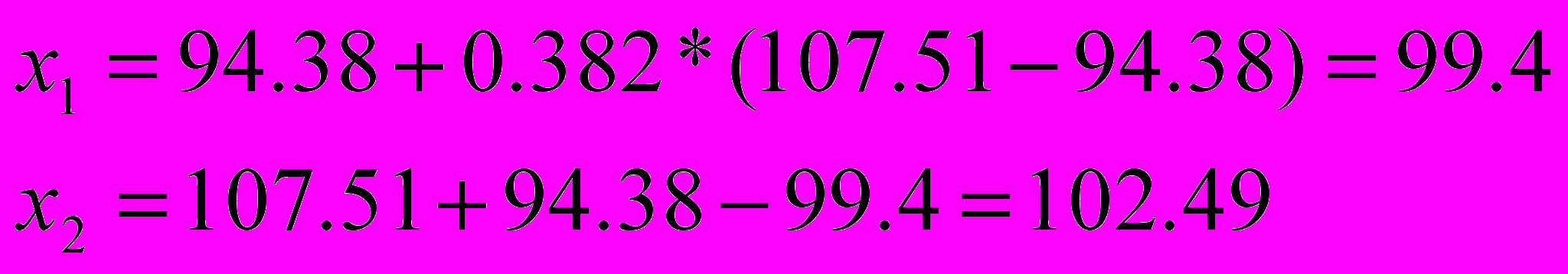
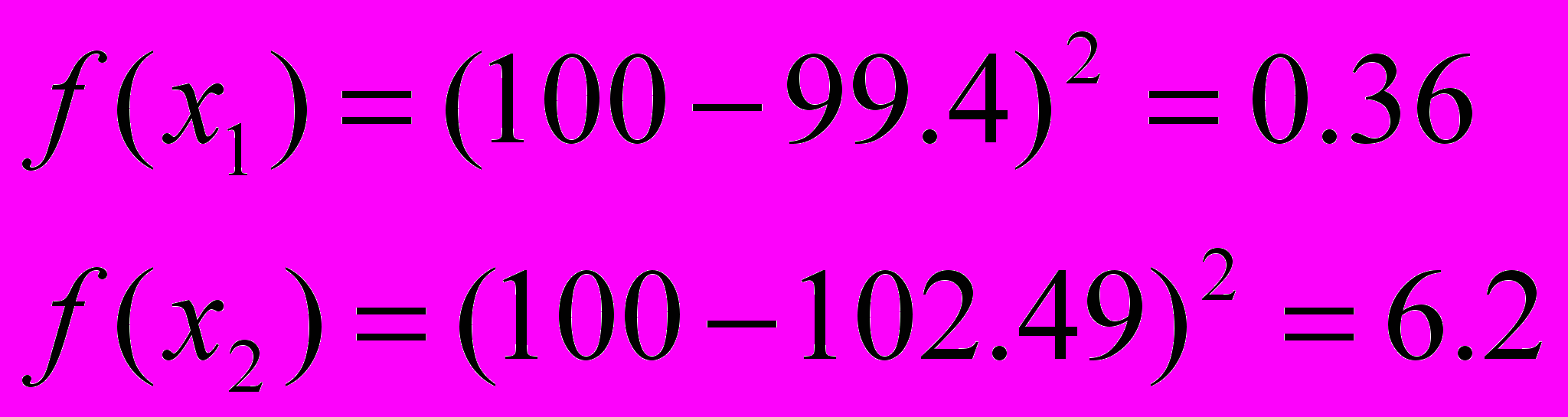
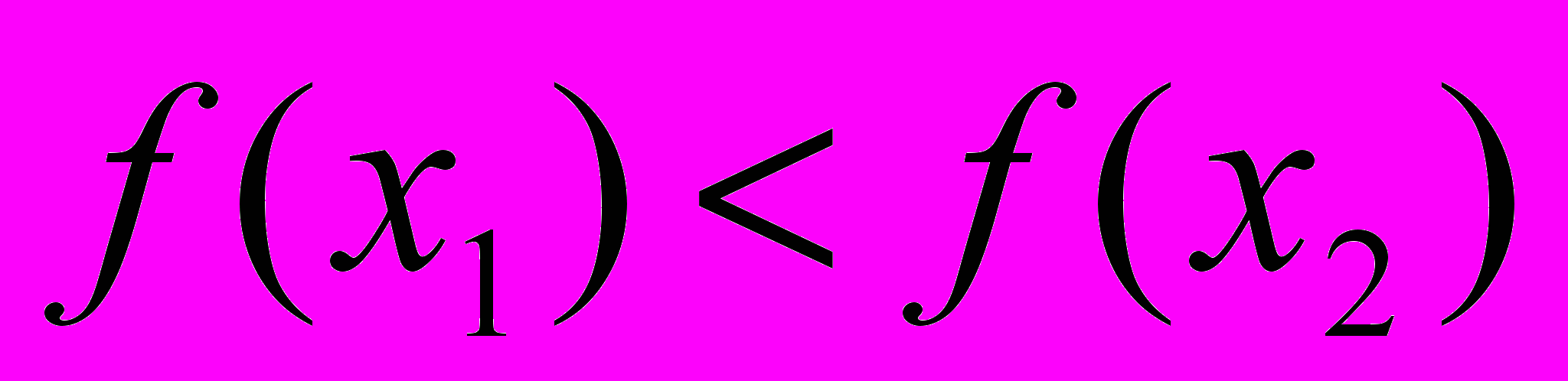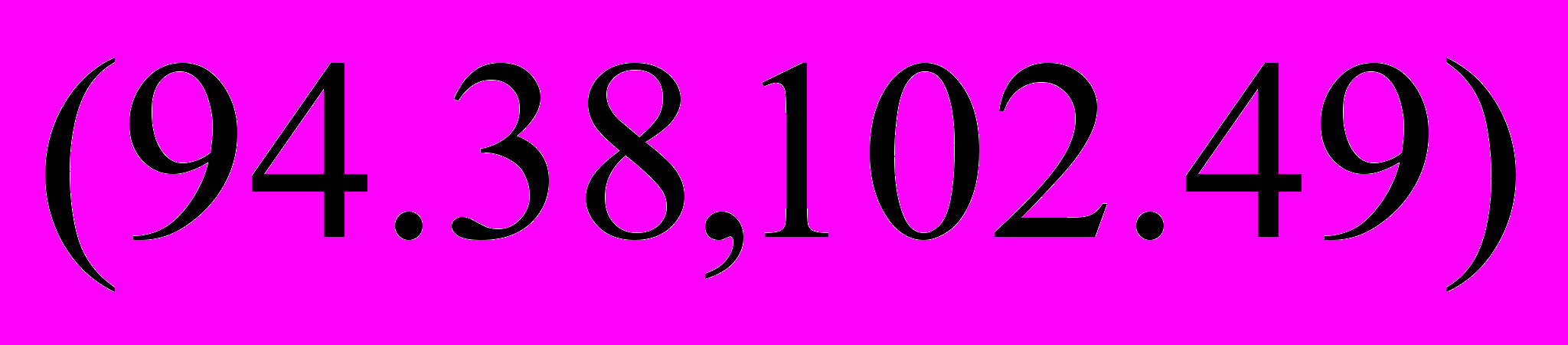
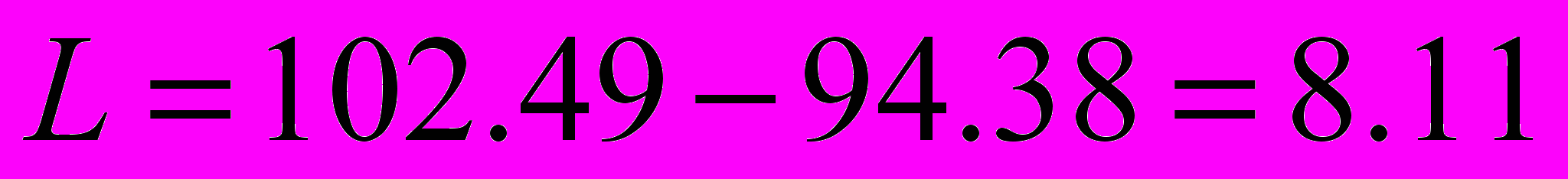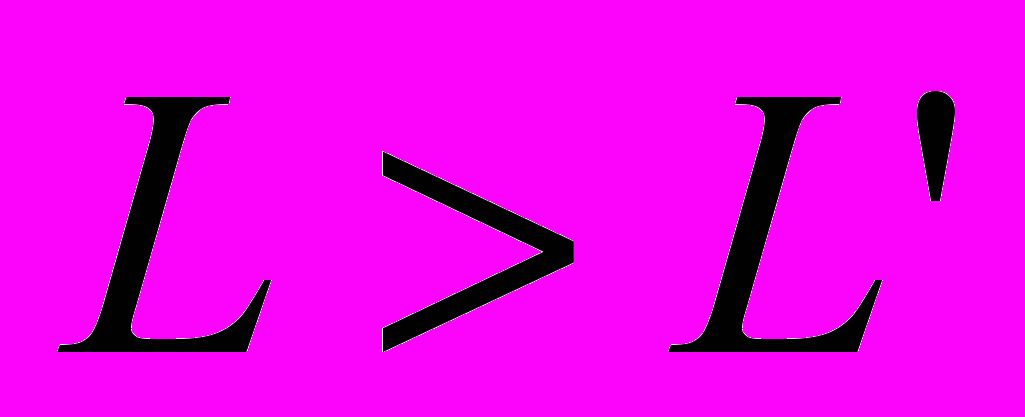
=> Итерация 6.
, 
=> 
=> 
=>
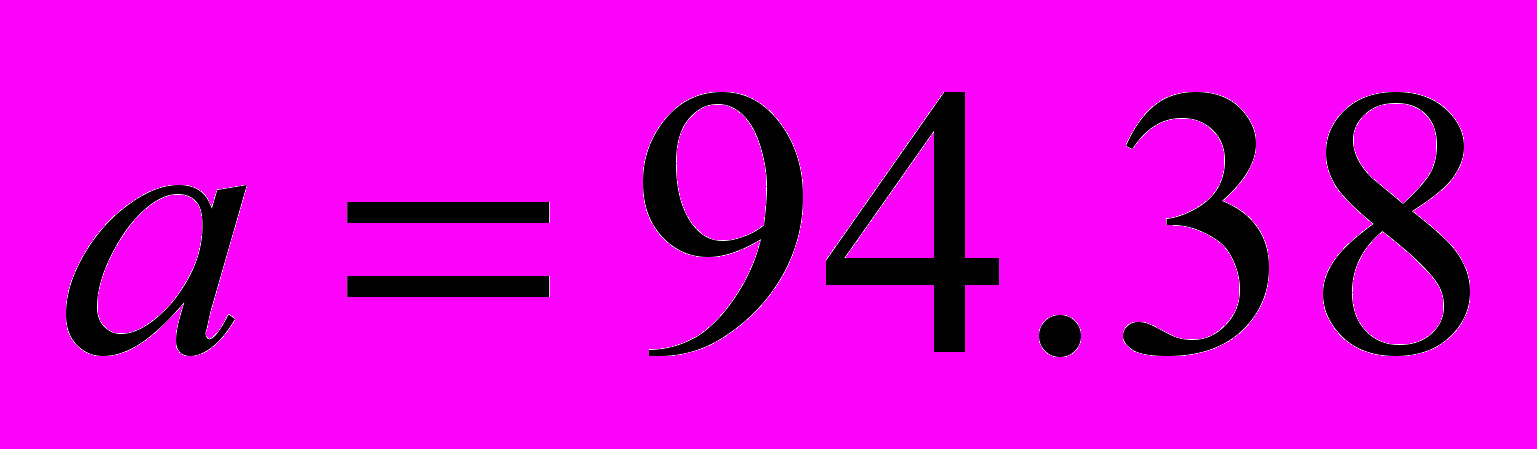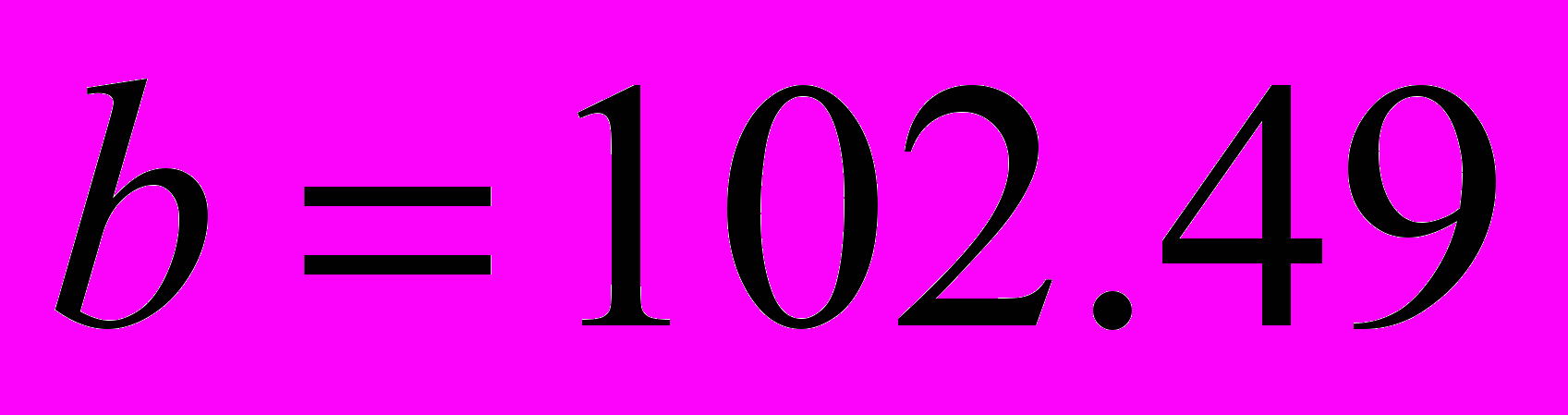
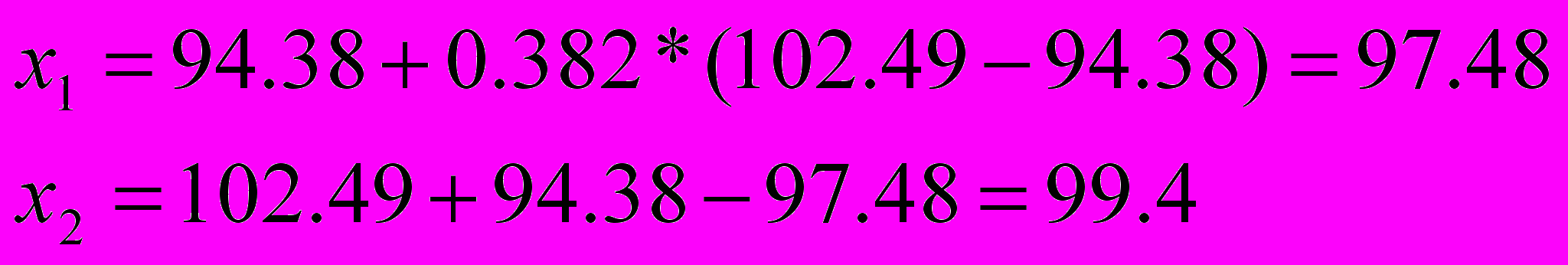
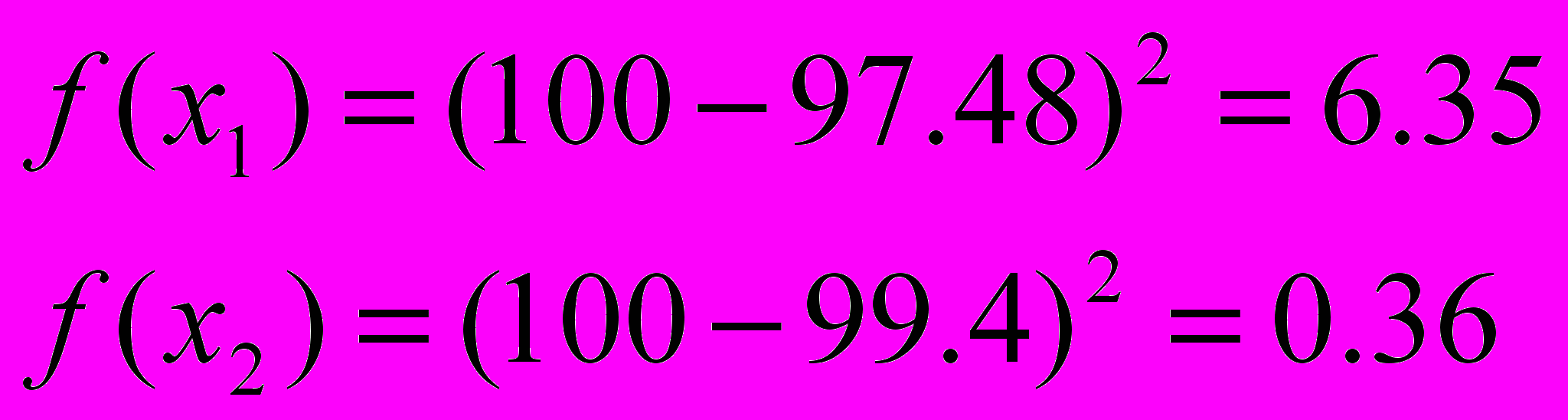
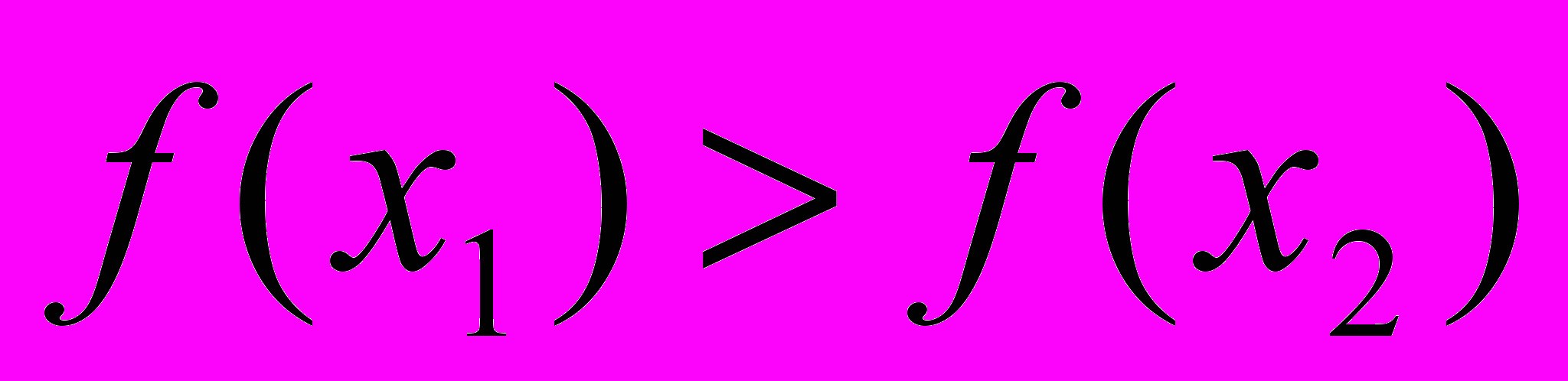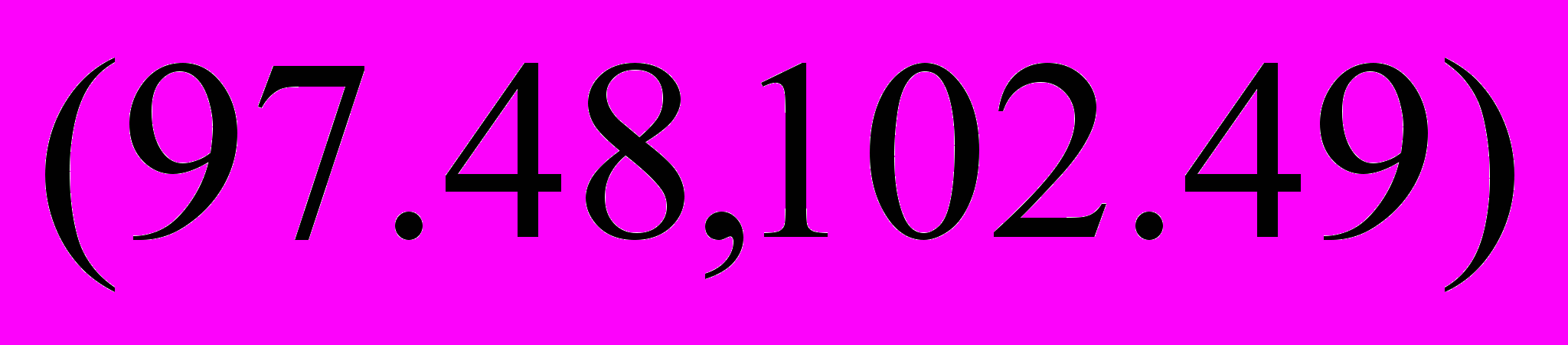
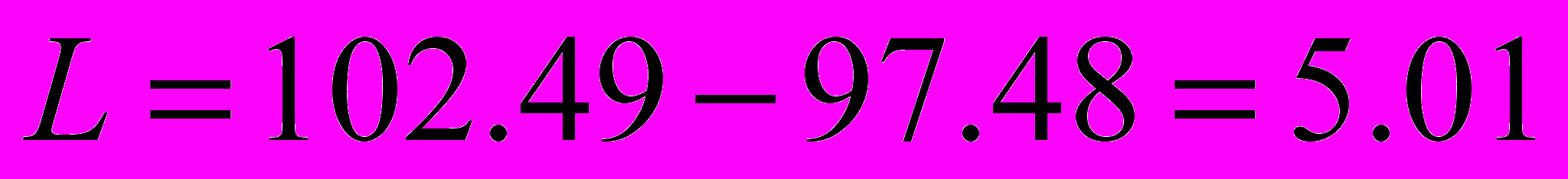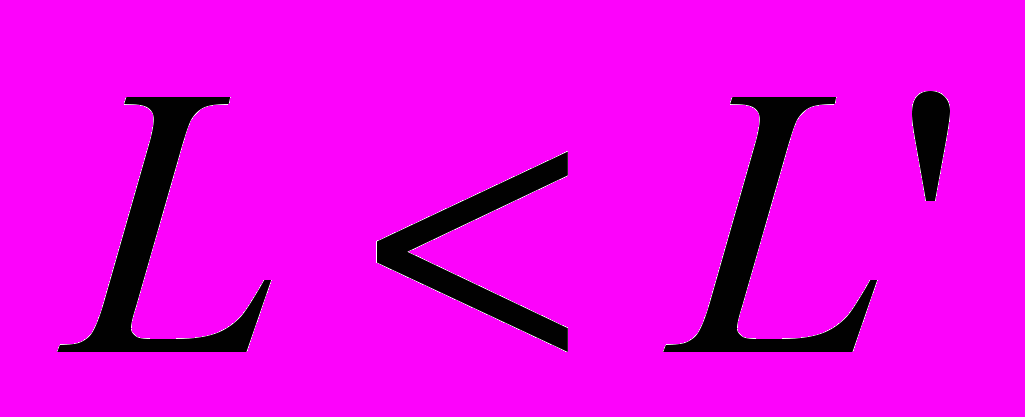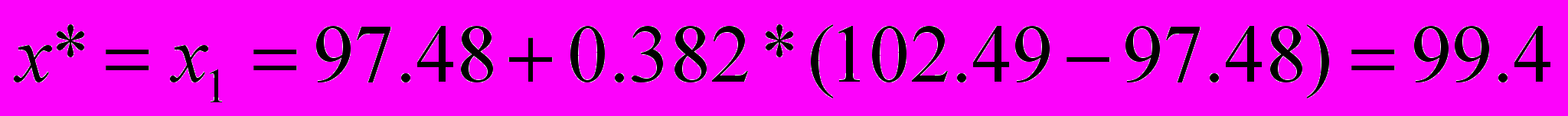-точка золотого сечения и есть точка минимума.Рассмотренные выше методы решения задач относятся к численным методам решения задач. Любой численный метод решения задачи основан на точном или приближенном вычислении характеристик задачи (значений целевой функции, значений функций, задающих допустимое множество, а также их производных).
В зависимости от того, какая информация используется, различают следующие методы. Если используется только значение функции, то такие методы называются методами нулевого порядка. К ним относятся рассмотренные нами ранее "Метод деления отрезка пополам", "Метод золотого сечения" и "Метод Фибоначчи".
Если при решении задачи используются не только значения функции, а еще и значения первой производной, то такие методы называют методами первого порядка.
Методы, использующие еще и значения второй производной, называются методами второго порядка.