Урок по теме: «Признаки равенства треугольников»
| Вид материала | Урок |
- Урок по геометрии в 7 классе по теме: «Признаки равенства треугольников», 60.74kb.
- Разработка урока по теме «Признаки равенства треугольников», 53.91kb.
- Урок геометрии в 7 классе по теме: Применение признаков равенства треугольников к решению, 75.1kb.
- А. С. Пушкина р п. Колышлей Пензенской области Геометрия и сказки А. С. Пушкина Повторительно, 36.32kb.
- Урока : обобщение и систематизация знаний учащихся по теме «Признаки равенства треугольников», 41.48kb.
- Урок по теме «Первый признак равенства треугольников», 38.38kb.
- Ятманкина Галина Михайловна моу саврушская сош с. Савруха Похвистневский район Самарская, 34.69kb.
- Проект представляет разработку темы: «Признаки равенства треугольников», 62.44kb.
- Тема: III признак равенства треугольников, 37.97kb.
- Тема урока : Решение задач по теме: «Признаки равенства треугольников», 17.66kb.
Обобщающий урок по теме:
«Признаки равенства треугольников»
УРОК ОТРАБОТКИ И ЗАКРЕПЛЕНИЯ ЗНАНИЙ.
Учебник «Геметрия. 7 класс.» Авторы : Л.С. Атанасян, В.Ф. Бутузов и др.
Зоренко Светлана Вениаминовна
учитель математики
МОУ г. Мурманска средняя общеобразовательная школа № 49
Цели и задачи урока:
1. Образовательные – в результате изучения признаков равенства треугольников учащиеся должны знать формулировки трех признаков , уметь решать задачи с использованием данных признаков.
2. Развивающие – продолжить дальнейшую работу по выработке умения сравнивать математические понятия, находить сходства и различия, умения наблюдать, подмечать закономерности, проводить рассуждения по аналогии; сформировать умение строить и интерпретировать математическую модель некоторой реальной ситуации.
3. Воспитательные – содействовать воспитанию интереса к математике и ее приложениям, активности, умению общаться, аргументировано отстаивать свои взгляды.
Оборудование: компьютер, проектор или интерактивная доска.
Ход урока
| Содержание учебного материала | Деятельность учителя | Деятельность учащихся |
| | - Двум ученикам вашего класса, Андрею и Алеше было дано задание: сделать модели двух равных треугольников. Алеша сделал эту модель. Она на доске. Андрей не смог сделать модель. | Андрей: Я позвонил Алеше, вспомнив, что не изготовил модель, и попросил его дать измерения треугольника. Алексей: Я сказал, что стороны моего треугольника 5см, 7 см, 10 см. |
| - Итак, у Андрея образца нет, ему известны только 3 стороны треугольника. Какой признак равенства треугольника будет использовать Андрей при построении модели? | Уч-ся: 3 признак. Проговаривают, как он читается. | |
| | | Андрей: Я не смог построить треугольник, зная только стороны треугольника. Алексей: Тогда бери транспортир. |
| - Ребята, как мог поступить Андрей в этой ситуации? | Уч-ся: можно построить треугольник по 2ум сторонам и углу между ними(1 пр.), можно по стороне и двум прилежащим к ней углам ( 2 пр.) | |
| | Андрей на доске выполняет это построение. | |
| - Алеша, проверь, равны ли ваши треугольники. | Снимается модель и накладывается на построенный треугольник. | |
| - Итак, мы повторили все признаки равенства треугольников и эту ситуацию мы вспомним, когда будем выполнять построение треугольника по 3ем элементам. - А теперь применим эти признаки для решения задач на доказательство. | | |
| Проецируется чертеж: 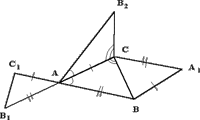 | - Назвать треугольники, равные треугольнику АВС и указать признак. | Уч-ся: 1)  АВС= АВС= АВ2С( по 2 признаку) АВ2С( по 2 признаку)2)  АВС= АВС= А1ВС( по 3 признаку) А1ВС( по 3 признаку)3)  АВС= АВС= АВ1С1(по 1 признаку) АВ1С1(по 1 признаку) |
| Проецируется чертеж:  Дано: АВ=ВС АF- биссектриса 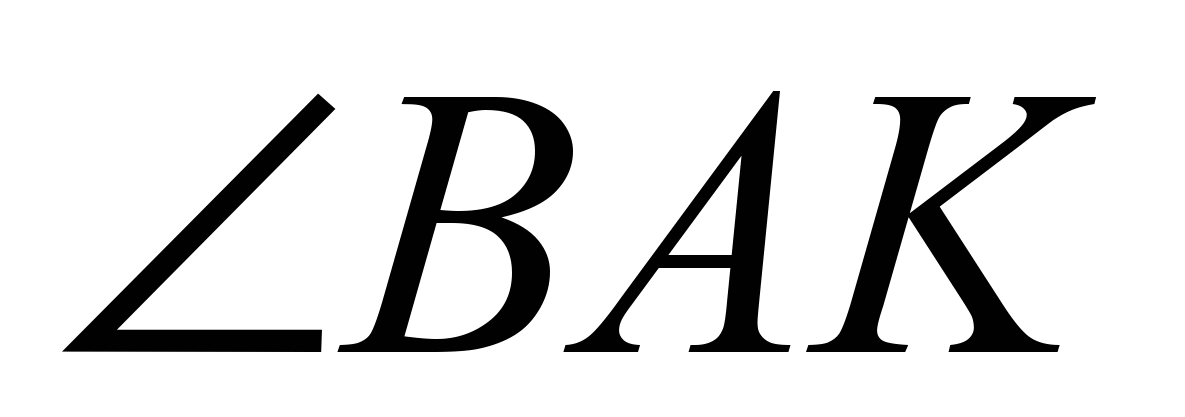 СД -биссектриса  Доказать:  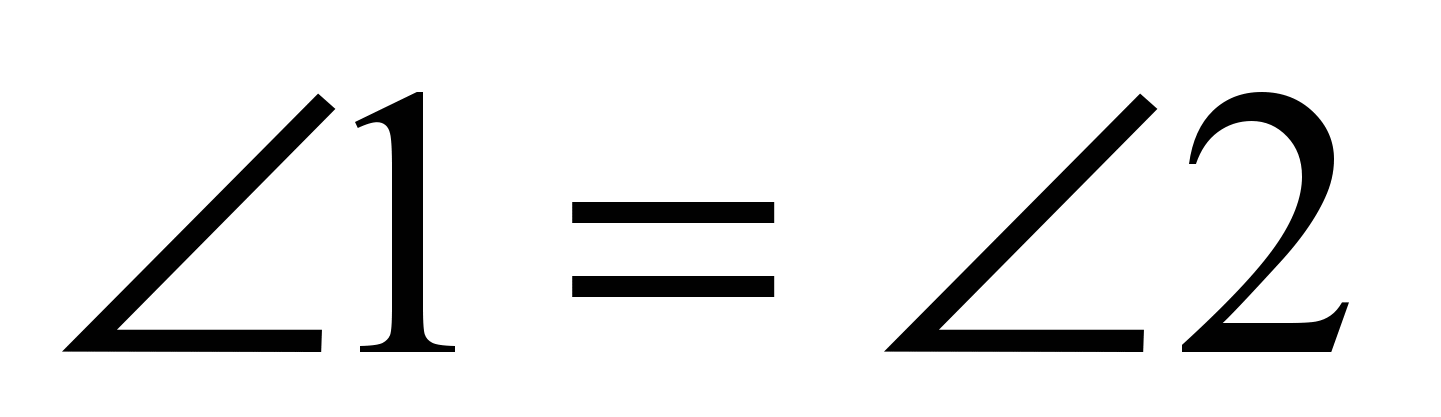 | - Попрошу запомнить результат этой задачи, т.к. он нам пригодится при решении других задач. | Уч-ся: Доказывают это утверждение устно. |
| Проецируется чертеж: 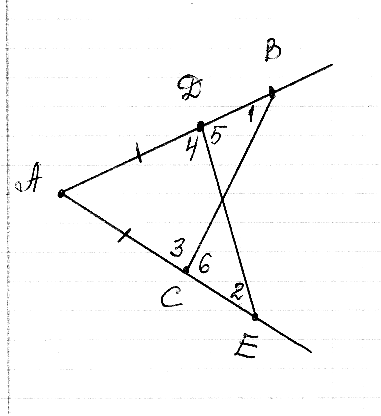 | - На одой стороне угла с вершиной А отмечены точки Д и В, на другой стороне угла С и Е так, что АД=АС=3см, АВ=АЕ=4 см. Докажите ,что: А) ВС=ЕД Б)КВ=КЕ, где К – точка пересечения отрезков ДЕ и ВС. - Я уверена, что с 1ой частью задачи вы справитесь сейчас самостоятельно. Доказательство запишите в тетрадь. - 2 часть сложнее. Прошу быть внимательными при обсуждении доказательства, т.к. предстоит оформить доказательство самостоятельно в тетради. | Уч-ся сам-но в тетради доказывают 1 часть ( 7 мин). - А теперь проверьте себя. (проецируется доказательство на доске) Док-во: А) Рассмотрим  АВС и АВС и  АДЕ: АДЕ:АВ=АЕ(по усл) АД=АС(по усл)  А-общий А-общий__________________   АВС= АВС= АДЕ(по 2 пр.) АДЕ(по 2 пр.) ВС=ЕД Б) 2 часть обсуждается вместе с уч-ся, оформляется доказательство сам-но. Док-во: 1) т.к.  АВС= АВС= АДЕ, то АДЕ, то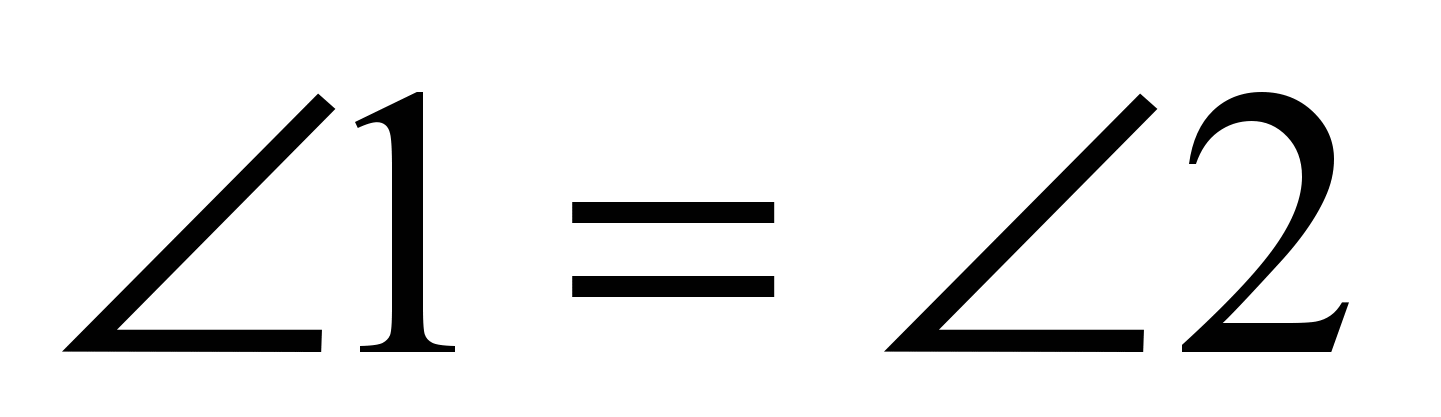  Т.к.  и и  4- смежные, то 4- смежные, то 5=1800- 5=1800- 4. 4.Т.к.  3 и 3 и  6- смежные, 6- смежные,то  6=1800- 6=1800- 3; но 3; но 3= 3= 4 4   5= 5= 6. 6.2) Рассм.  ДКВ и ДКВ и  СКЕ: СКЕ:ДВ=СЕ(по усл.)  1= 1= 2(по п.1.) 2(по п.1.) 5= 5= 6(по п.1.) 6(по п.1.)__________________   ДКВ= ДКВ= СКЕ(по 2 пр.) СКЕ(по 2 пр.) КВ=КЕ Что и требовалось доказать. |
 | - А теперь начертите окружность с центром в точке О. Проведите 2 равные хорды, не имеющие общих точек. Проведите из центра окружности перпендикуляры к хордам. - Я тоже это построила(проецируется чертеж , проверяется построение). Обозначьте хорды MN и EF, основания перпендикуляров Р и Д. Докажите равенство отрезков ОР и ОД. | Сначала проводится анализ задачи. План решения записывает учитель на доске: 1) Сначала ввести в рассмотрение  , в которых ОР и ОД являются сторонами. Это , в которых ОР и ОД являются сторонами. Это  РОМ и РОМ и  ДОЕ. ДОЕ.2)Ищем равные элементы в этих  : :ОМ=ОЕ=R. 3)Вводим в рассмотрение другие  . Это . Это  MON и MON и  EOF.Докажем их равенство: EOF.Докажем их равенство:NO=OF=R OE=OM=R MN=EF(по усл.) ________________   MON= MON= EOF(по 3 пр.) EOF(по 3 пр.)  1= 1=  2, 2, MON= MON= EOF. EOF.4)Определяем вид  MON и MON и  EOF- равнобедренные. EOF- равнобедренные.По св-ву равнобедренного треугольника OP,OD –биссектрисы,  6= 6= 3. 3.5) Рассм.  МОР и МОР и  ЕОД: ЕОД:МО=ЕО=R  1= 1= 2(по п.2.) 2(по п.2.) 6= 6= 3(по п.4.) 3(по п.4.)_____________________   МОР= МОР= ЕОД(по 2 пр.) ЕОД(по 2 пр.) ОР= ОД. (Рассм. устно другой способ решения задачи, начиная с п.4. использовать свойство медианы, а не биссектрисы) |
