Тема Решение задач на применение признаков равенства треугольников
| Вид материала | Решение |
- Урок по теме: «Признаки равенства треугольников», 57.32kb.
- Урок геометрии в 7 классе по теме: Применение признаков равенства треугольников к решению, 75.1kb.
- Разработка урока по теме «Признаки равенства треугольников», 53.91kb.
- Урок по геометрии в 7 классе по теме: «Признаки равенства треугольников», 60.74kb.
- Рабочая программа по математике 9 класс, 1286.09kb.
- Тема урока : Решение задач по теме: «Признаки равенства треугольников», 17.66kb.
- Тема: III признак равенства треугольников, 37.97kb.
- А. С. Пушкина р п. Колышлей Пензенской области Геометрия и сказки А. С. Пушкина Повторительно, 36.32kb.
- Темы вашего учебного проекта Первый признак равенства треугольников, 65.14kb.
- Урока : обобщение и систематизация знаний учащихся по теме «Признаки равенства треугольников», 41.48kb.
Тема Решение задач на применение признаков равенства треугольников.
Цели:
Образовательная :знать формулировки признаков равенства
треугольников, закрепить навыки в решении
задач на применение этих признаков,
подготовить учащихся к предстоящей
контрольной работе;
Развивающая: развивать логическое мышление,
пространственное воображение, умение
выделять главное в задачах, видеть по
рисункам элементы признаков равенства
треугольников;
Воспитательная: воспитывать интерес к геометрии через игру,
через путешествие , культуру устной речи,
правильное и аккуратное оформление
геометрических задач
Ход урока: 1.Организационный момент.
2.Повторение. Игра «Ответь и задай вопрос товарищу».
3. Чтение рисунков по готовым плакатам (устно).
4. Решение задач в тетрадях.
5. Дифференцированная самостоятельная работа.
6. Занимательная страница.
7.Домашнее задание. Итог урока.
1. Наш урок посвящен решению задач на применение признаков равенства треугольников.
Сегодня мы продолжим путешествие по прекрасной стране Геометрия. Лучше разглядим ее красоту и совершенство.Девизом нашего урока будет: «С любовью к ее величеству- науке геометрии». Пройдемся по ее памятным местам- определениям и теоремам. В геометрии очень много разных тропинок, но главная из них та, которая начинается за школьной партой и учебной книгой.
Мы с вами уже побывали на тропинке решения задач и доказательства теорем ( на доске висит большой рисунок, где указаны различные тропинки , памятные места страны Геометрия).Сегодня вновь вернемся к тропинке решения задач и побываем на тропинке красоты чисел. Шагая по тропинкам, погрузимся в мир треугольников. В геометрию тропинки одолеем без запинки. При этом наши суждения должны отличаться строгостью, обоснованностью, краткостью и полнотой, последовательностью и завершенностью, так же не будем пренебрегать интуицией, догадкой, фантазией. Итак, в добрый путь!
Работаем группами, у каждой группы есть свой консультант, они будут оценивать ваши ответы и отмечать в ваших маленьких дневниках.
2.Игра «Ответь и задай вопрос товарищу». Каждый задает по два вопроса и отвечает на два. Консультант учитывает правильную формулировку вопроса, ее оригинальность и , конечно же, ваши ответы.
3. Каждый из вас получает карточку с рисунком. Вам нужно ее прочитать, т. Е. по рисунку выделить данные и доказать, что треугольники будут равны. Сейчас каждый из вас подходит к любому из гостей и отвечает.
А теперь прочитаем чертеж на доске. Выделить данные и доказать, что треугольники будут равны.
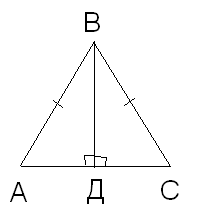
Данные:
∆АВС- равнобедренный, ВД-высота.По какому признаку можно доказать, что ∆АВД= ∆ВДС ?
Рассмотрим ∆АВД и ∆ВДС,
1)по первому признаку равенства АВ = ВС,т.к. ∆АВС- равнобедренный;АД= ДС, т.к. ВД в равнобедренном треугольнике будет медианой;
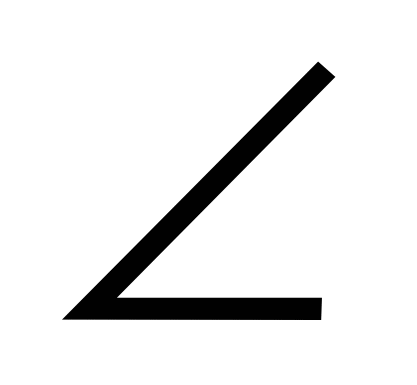А= 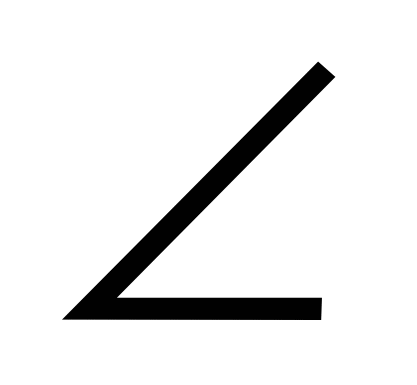С,т.к. углы при основании в равнобедренном треугольнике равны.2)По второму признаку равенства: ВД – общая;
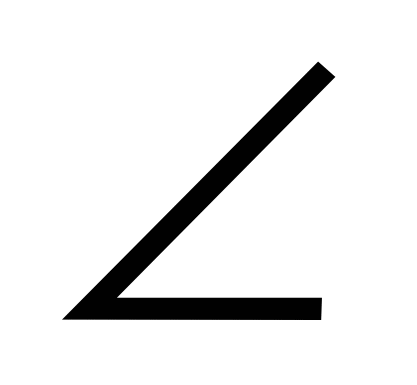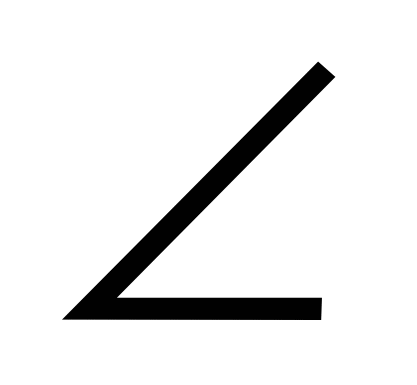АДВ=СДВ; 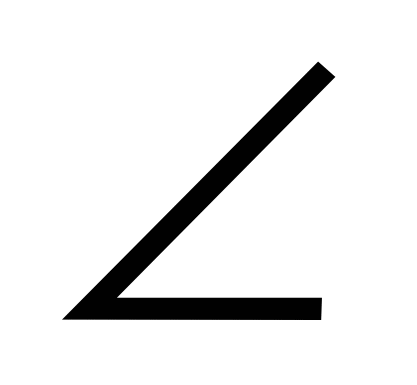АВД=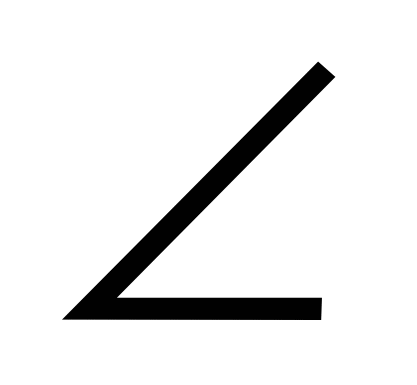СВД т.к. ВД будет биссектрисой.3)По третьему признаку равенства: АВ=ВС; ВД – общая; АД=ДС.
4 Решаем две задачи в тетрадях.
1)Дано: АВ=АС;
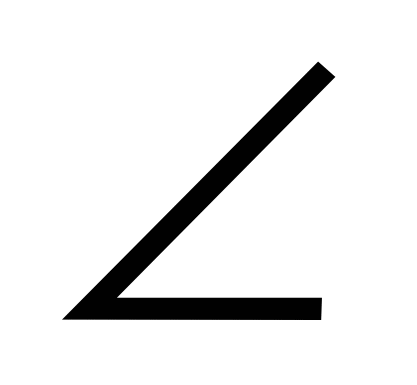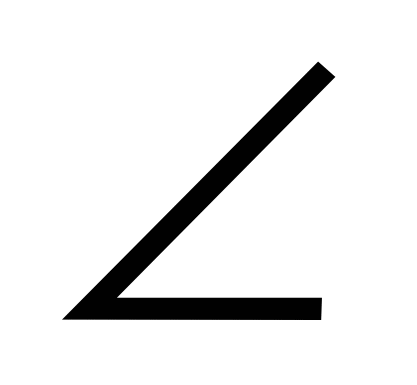АСЕ=АВД;Доказать: ∆АСЕ=∆АВД
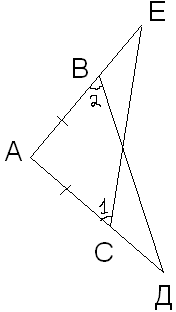
Д-во: Рассмотрим ∆АСЕ и ∆АВД. т.к. угол А – общий, АС=АВ,
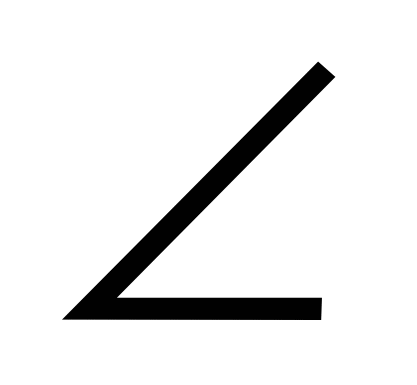1=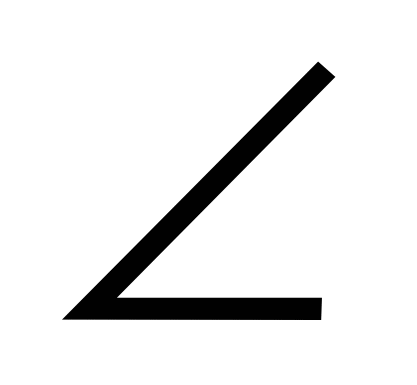2, то ∆АСЕ=∆АВД (второй призн. равенства)2) (задача на карточке) Отрезки МЕ и РК точкой Д делятся пополам. Докажите, что
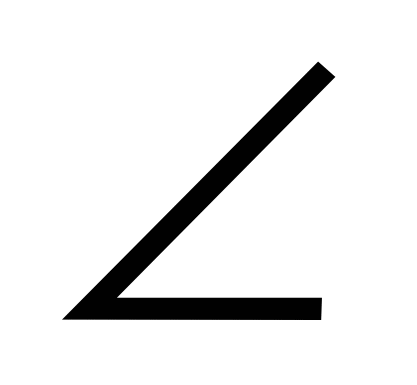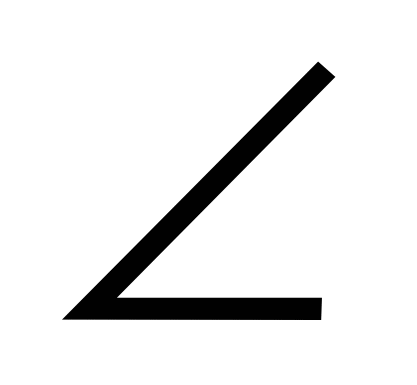КМД=РЕД.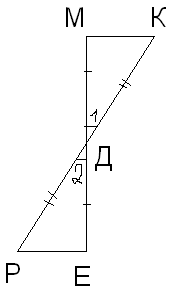
Дано: МД=ДЕ; РД=ДК
Д-ть:
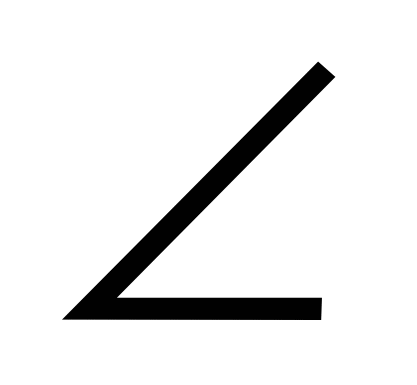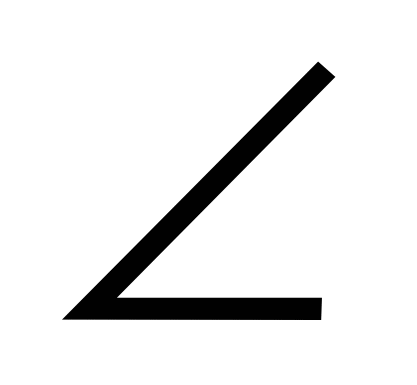КМД=РЕДД-во: Рассмотрим ∆РЕД и ∆МДК. Т.к. МД=ДЕ; КД=ДР;
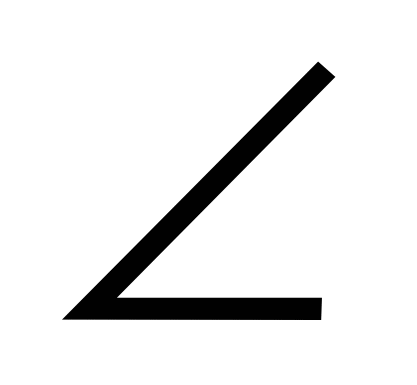1=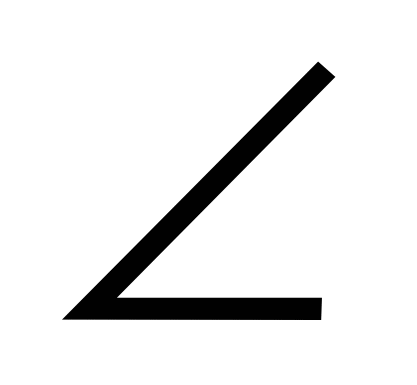2 (вертик.), то ∆РЕД=∆МДК (первый призн. тр.) Сл-но, 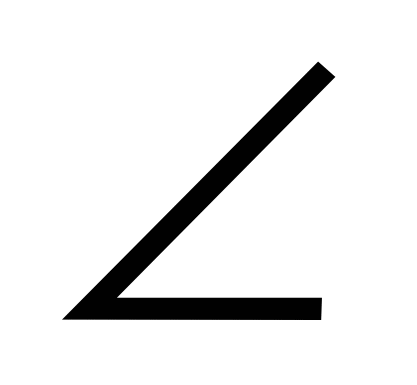КМД=РЕД.5 На столах в конвертах разноцветные карточки с задачами, по желанию выбираете любую одну, но напоминаю, что синяя – на «3»; желтая на «4», красная – на «5». Решаем в тетрадях. Кто решит, дает на проверку консультантам и получает оценку.
6 В начале урока я говорила, что будем проходить по двум тропинкам, по одной из них мы уже прошли, а теперь пройдемся по тропинке красоты геометрии.
Сказка.
Действующие лица: автор, определение, теорема, доказательство и задача.
Автор: разговорились как-то определение, теорема, доказательство и задача.
Определение: Мы, определение, основа всей геометрии. Без нас и геометрии не было! Если человек попадает на необитаемый остров без учебников и с ним будем все мы, то он, опираясь на нас создает всю остальную геометрию. Значит мы основа основ.
Теорема: Хороша была бы геометрия, если бы не было нас, теорем! Любой школьник с грустью улыбнется, представив, что за геометрия без нас была бы. Ничего, кроме определений. А вот мы, теоремы царствуем по всему учебнику геометрии!
Доказательство: Не ссорьтесь. Без меня и определения ни к чему. Зачем они тогда! Без меня и вы, теоремы, не появились бы на свет. Но именя без вас бы не было. Разве можно считать доказательством рассуждения, которые опираются не на определения и теоремы, а на то, что кому-то придет в голову.
Задача: Вы забыли о нас, задачах. Ведь через нас только ученики и начинают вас по настоящему понимать и ценить. Из-за задач – и в вас нужда, а то бы вас и забыли.
Геометрия: Все вы правы, дети мои! У каждого из вас свои заслуги и достоинства. Но существуют они только тогда, когда вы все вместе. Коль не будет единства – не будет и достоинств ваших. Исчезнет кто-то из вас – погибнут остальные. И я, Геометрия, погибну.
Так будьте едины, дружны, помогайте друг другу и расскажите это тем, кто меня изучает. Все сказанное мной и вами важно прежде всего для изучающих, любящих и желающих познать меня.
(На доске плакат со стихотворением)
Думы нездешней полна,
Чуть загрустив от чего-то,
Молча стоит у окна,
В мыслях – задачи, задачи…
Да геометрии надо
Мир постигать наш – и вот
Страсть отстраненного взгляда
В прорву пространства ведет.
Пусть ей взгрустнется немножко,
Жалобы не услыхать…
Строгая, смотрит в окошко,
Сущее хочет познать
Да, геометрия от наших задач совсем стало грустно, мы сейчас постараемся её развеселить, заинтересовать занимательными задачами.
Дома вы должны были найти задачи по теме «Треугольник». Посмотрим их. Дети знакомят со своими задачами.
Посмотрите, Геометрия развеселилась, ей стало весело от ваших задач. Решить мы их не успеем, разберем их на факультативе.
7 Оценки за урок (по маленьким дневникам).
Домашнее задание: каждый забирает ту карточку, которая на столе.
Примерные задания для уроков: прочитать рисунок и доказать, что треугольники равны.
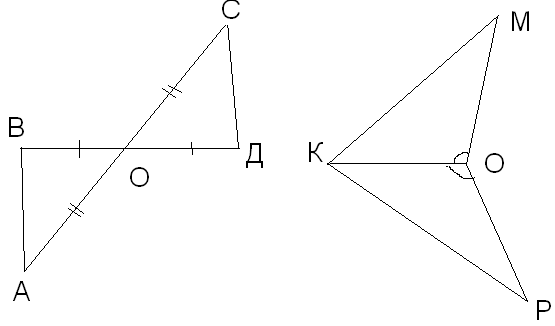
КО-биссектриса
Дифференцированная самостоятельная работа:
Карточка А (синяя)
1.Формулировка изученной теоремы, либо воспроизводство, либо прочтение чертежа.
2. Одношаговая задача на «распознавание» (увидел-решил).
Карточка Б(желтая)
1. Формулировка и доказательство изученной теоремы, либо решение несложной задачи на доказательство.
2.Задача на «распознавание», в решении которой могут быть использованы буквенные выражения или простейшие дополнительные построения, или задача на узнавание ранее изученных объектов в новых конфигурациях.
Карточка В(красная)
1. Формулировка и доказательство утверждения, которое не было рассмотрено в классе и которого нет в учебнике. Либо формулировка и воспроизведение доказательства теоремы, уровень сложности которого превосходит уровень обязательной подготовки.
2.Задача, для решения которой нужно либо сделать несколько логических шагов, либо использовать прием, связанный с дополнительным построением или применением ранее изученных фактов в новой ситуации, или же полноценная задача на «анализ-синтез».
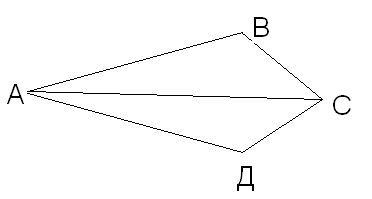
Синяя карточка: Так как АД=АВ и ВС=ДС, то ∆ВАС= ∆ДАС:а) по двум сторонам и углу между ними; б) по стороне и прилежащим к ней углам; в) по трем сторонам.
Желтая карточка: В равнобедренном треугольнике СДЕ с основанием ДЕ проведена биссектриса СК. Найдите СК, если периметр треугольника СДЕ равен 84 см, а периметр треугольника СКЕ равен 56 см.
Красная карточка: На сторонах угла Д отмечены точки М и К так, что ДМ=ДК. Точка Р лежит внутри угла Д и РК=РМ. Докажите, что луч ДР- биссектриса угла МДК.