Решение уравнения, то и TΨ

Вид материала

Решение

Содержание T на левую и правую часть уравнения Шредингера: THΨ=TEΨ H(TΨ)=E(TΨ) H делятся на два класса: симметричные относительно σ H будет иметь блочно-диагональный вид, т.е. , если 

Подобный материал:

• Найти частное решение линейного однородного дифференциального уравнения. Решение, 6.09kb.
• Календарный план чтения лекций, 27.51kb.
• Методы решения тригонометрических уравнений, 53.9kb.
• Урок по алгебре в 8-м классе по теме: «Определение квадратного уравнения. Неполные, 70.52kb.
• Дифференциальные уравнения (вопросы к экзамену), 26.43kb.
• Наибольший общий делитель. Наименьшее общее кратное, 326.23kb.
• П. В. Чулков, «Уравнения и неравенства в школьном курсе математики, лекции 1-4», стр, 8.44kb.
• Решение задач повышенной сложности по теме: «Уравнения и системы уравнений», 141.17kb.
• Урок математики в 6 классе по теме «Решение задач на составление уравнений», 98.1kb.
• Методика изучения уравнений в курсе алгебры 7-9 классов Примерное содержание, 12.53kb.

Благодарим всех за оказанную помощь.

Лекция 10

С={g_i}



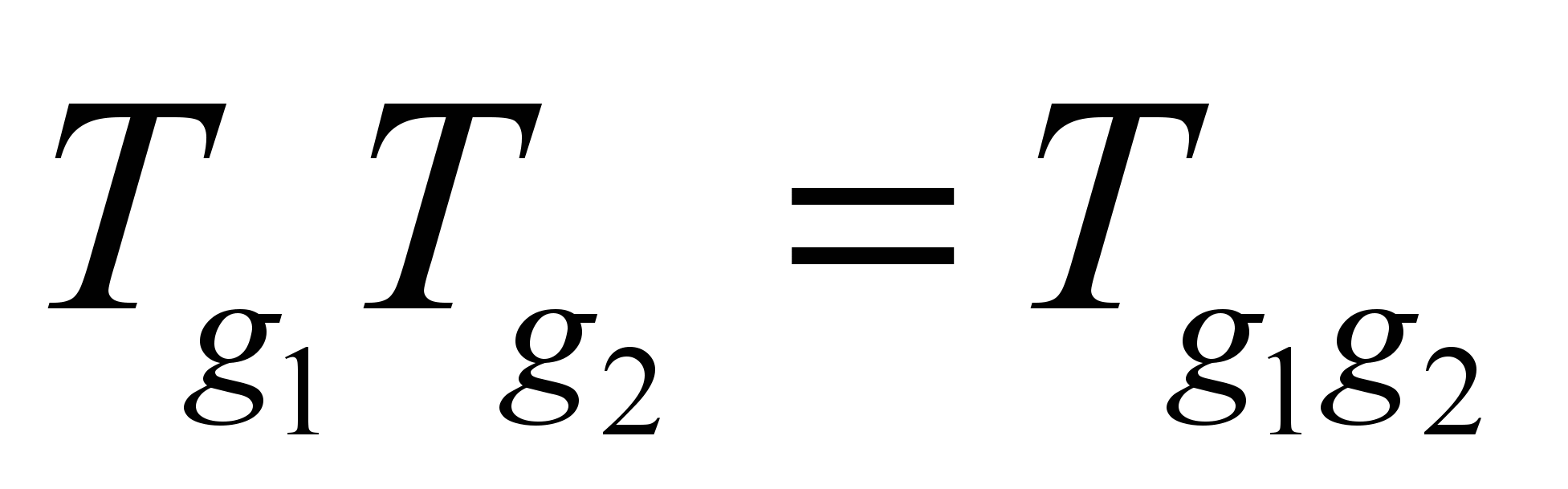
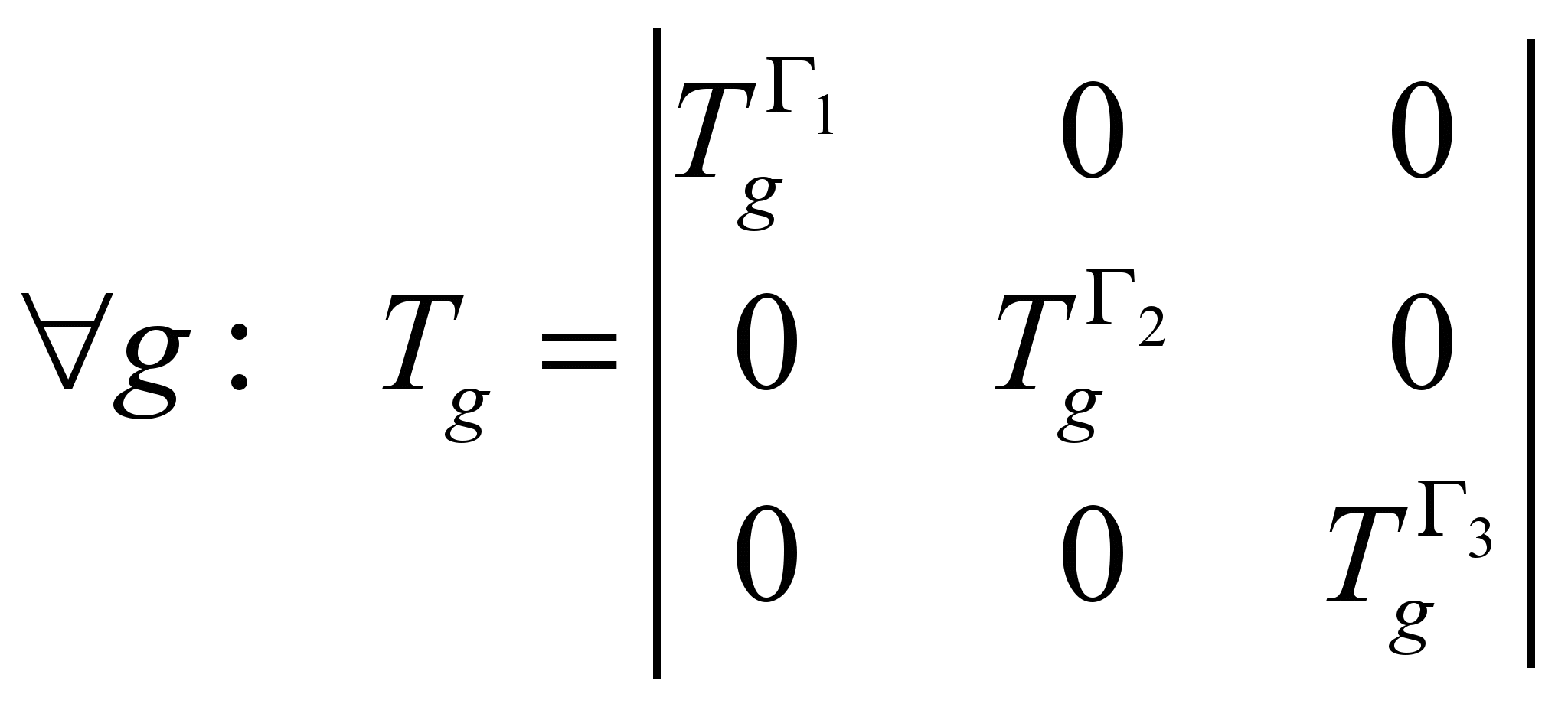, тогда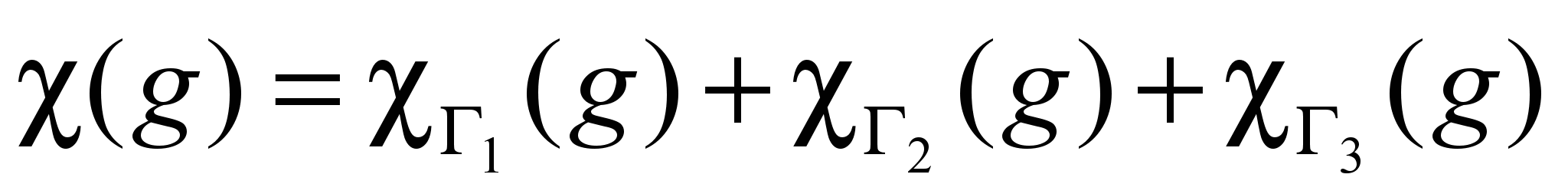



Рассмотрим уравнение Шредингера:



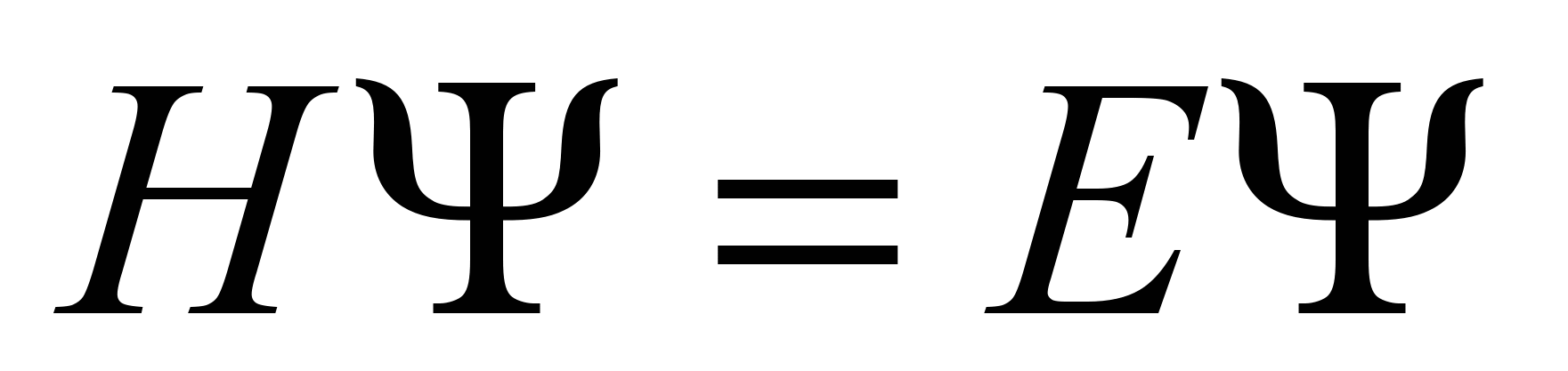
T – преобразование симметрии

THT^-1 – оператор Гамильтона в новом базисе

THT^-1=H  HT=TH

Операторы симметрии – это те операторы, которые коммутируются гамильтонианом.

Подействуем оператором T на левую и правую часть уравнения Шредингера:

THΨ=TEΨ

H(TΨ)=E(TΨ)

Если Ψ – решение уравнения, то и TΨ будет решением уравнения.

Собственные функции H образуют пространство, в котором есть представление оператора симметрии. Если H обладает некоторой симметрией и 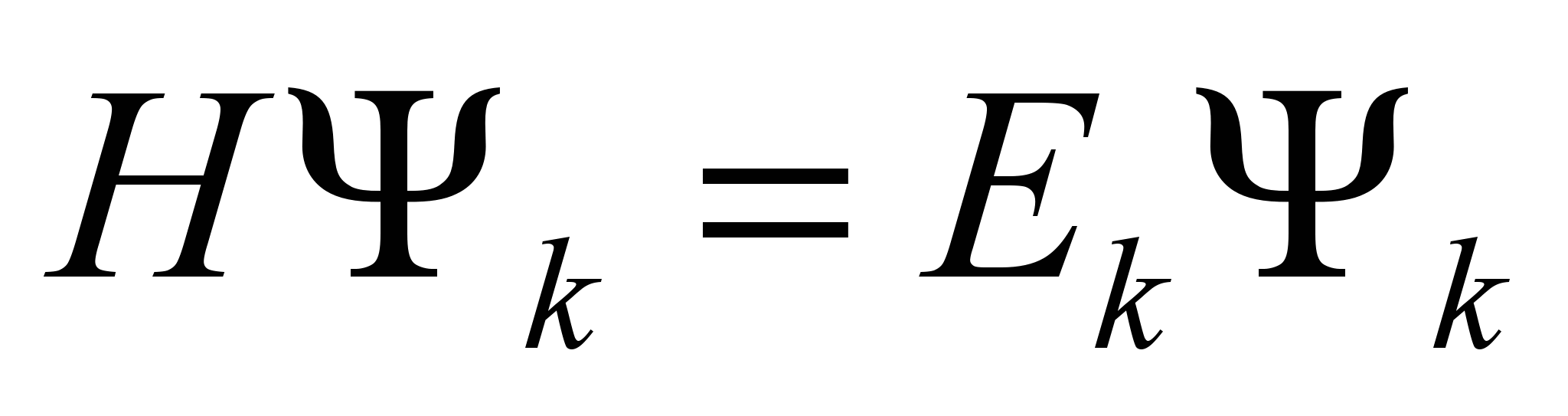, то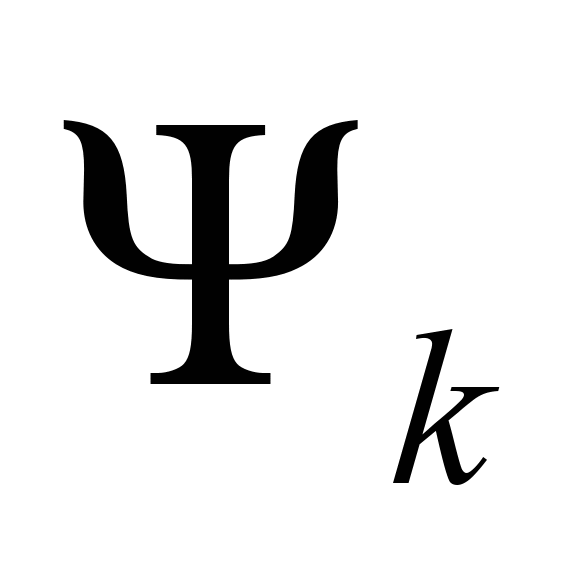

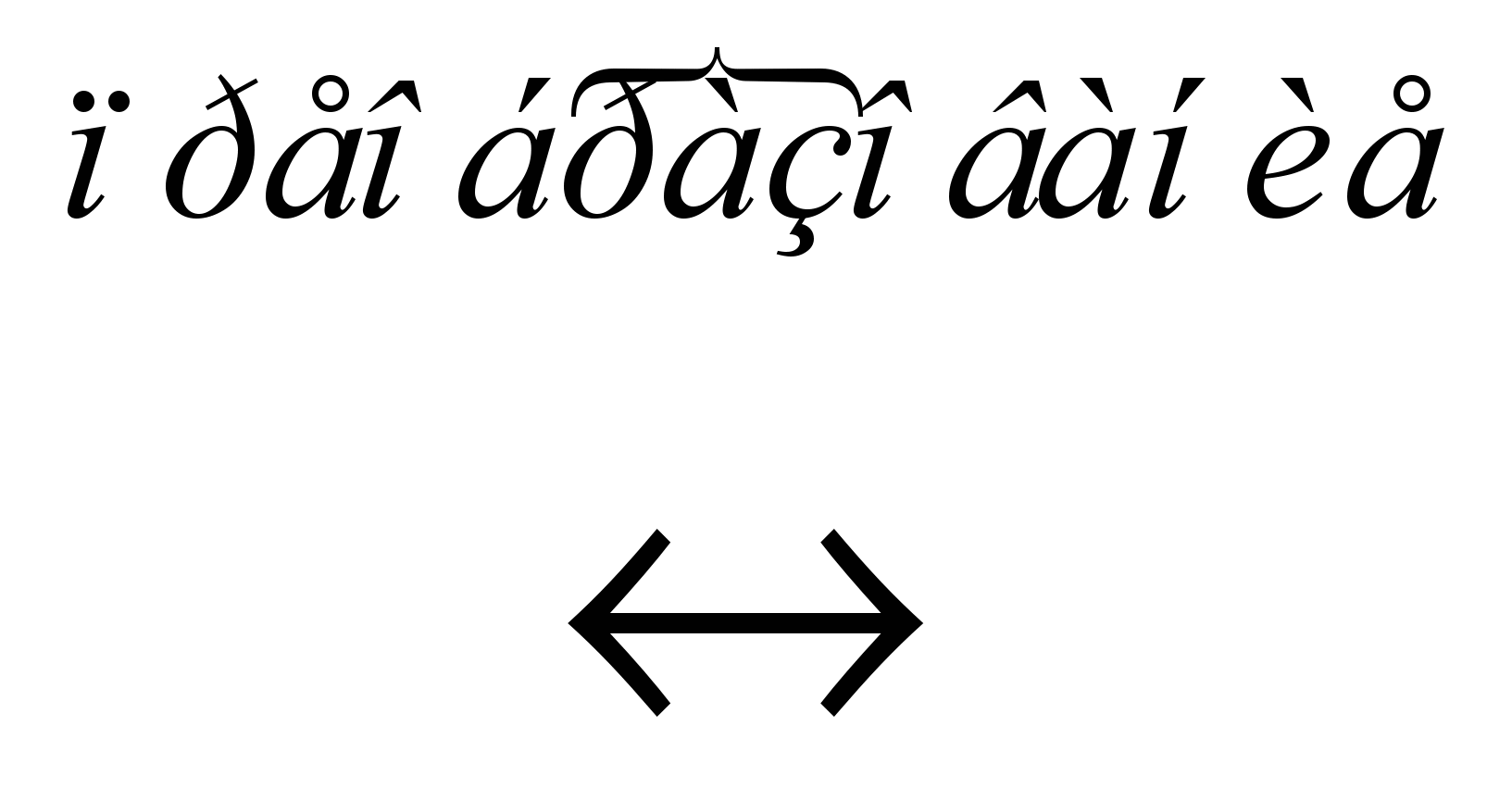неприводимые представления группы симметрии.

Например, рассмотрим потенциальный ящик:

Группа симметрии: (e, σ)

Таблица характеров:

	e	σ
a’	1	1
a’’	1	-1

Все собственные функции H делятся на два класса: симметричные относительно σ (функции Ψ₀, Ψ₂,…) и антисимметричные относительно σ (функция Ψ₁, Ψ₃,…).

Теорема: Функции, относящиеся к разным неприводимым представлениям, ортогональны между собой.

Если Г₁ и Г₂ – разные неприводимые представления, то:



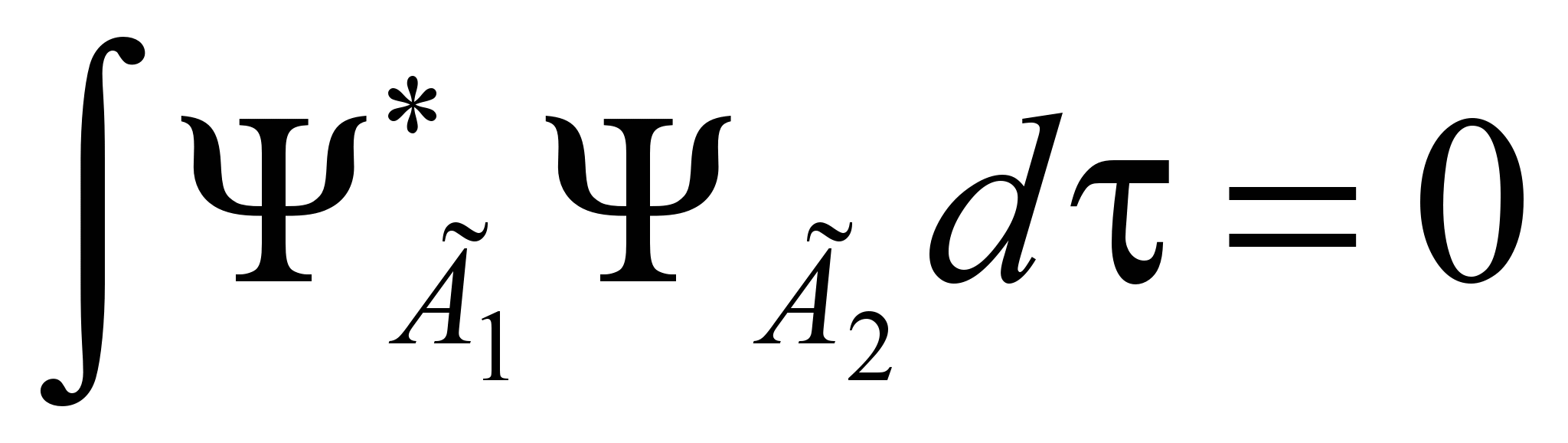
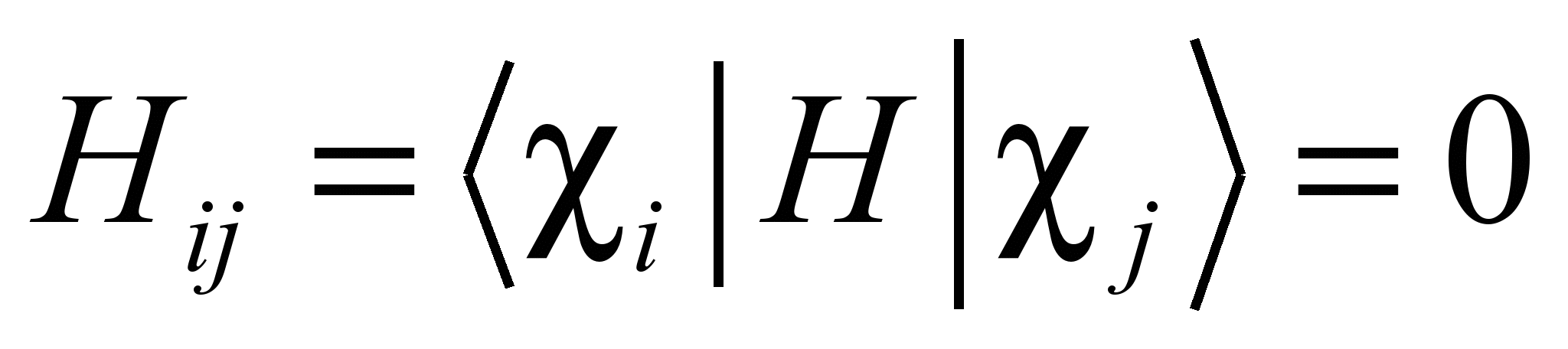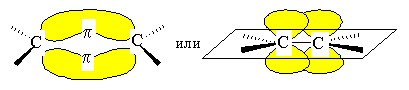
Матрица H будет иметь блочно-диагональный вид, т.е. , если _i и _j относятся к разным неприводимым представлениям.

Поясним вышесказанное при рассмотрении молекулы этилена:

1SH	σ	2Px		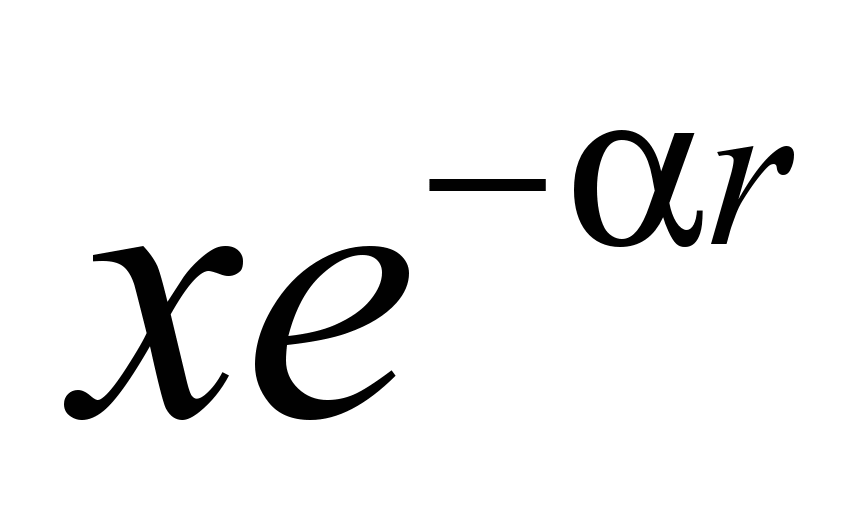σ
1SC	σ	2Py		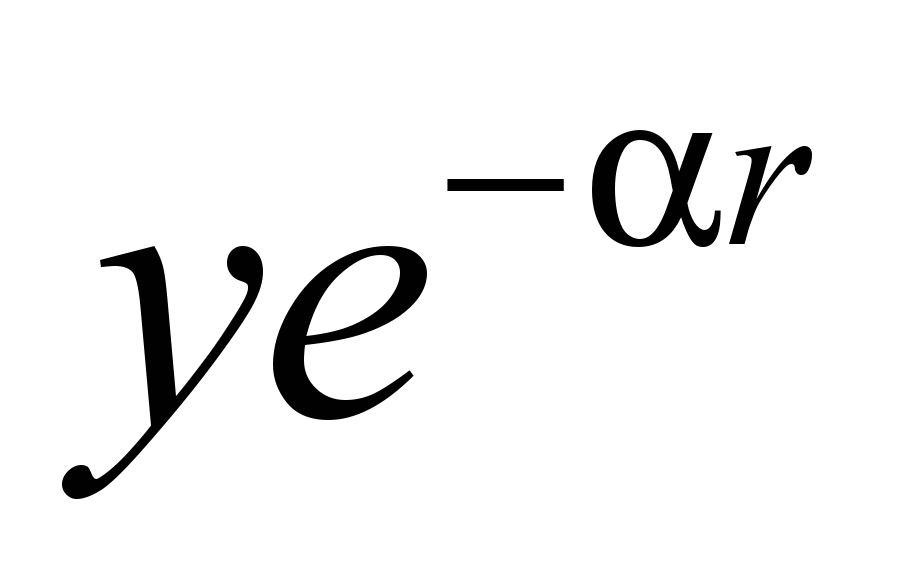σ
2SC	σ	2Pz		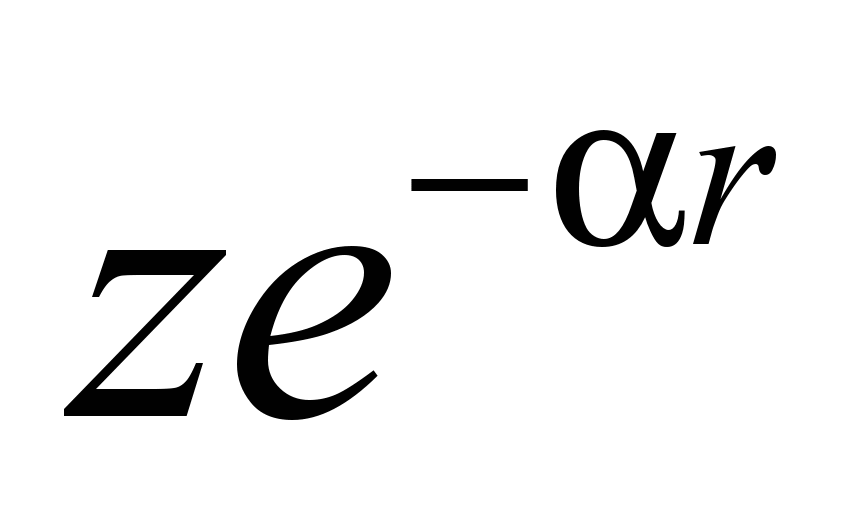π

У σ-орбиталей знак не меняется при отражении относительно плоскости молекулы, а у π-орбиталей знак меняется.

Уравнение Шредингера (и Хартри-Фока) будем решать отдельно для σ- и π-орбиталей.

Рассмотрим π-орбиталь 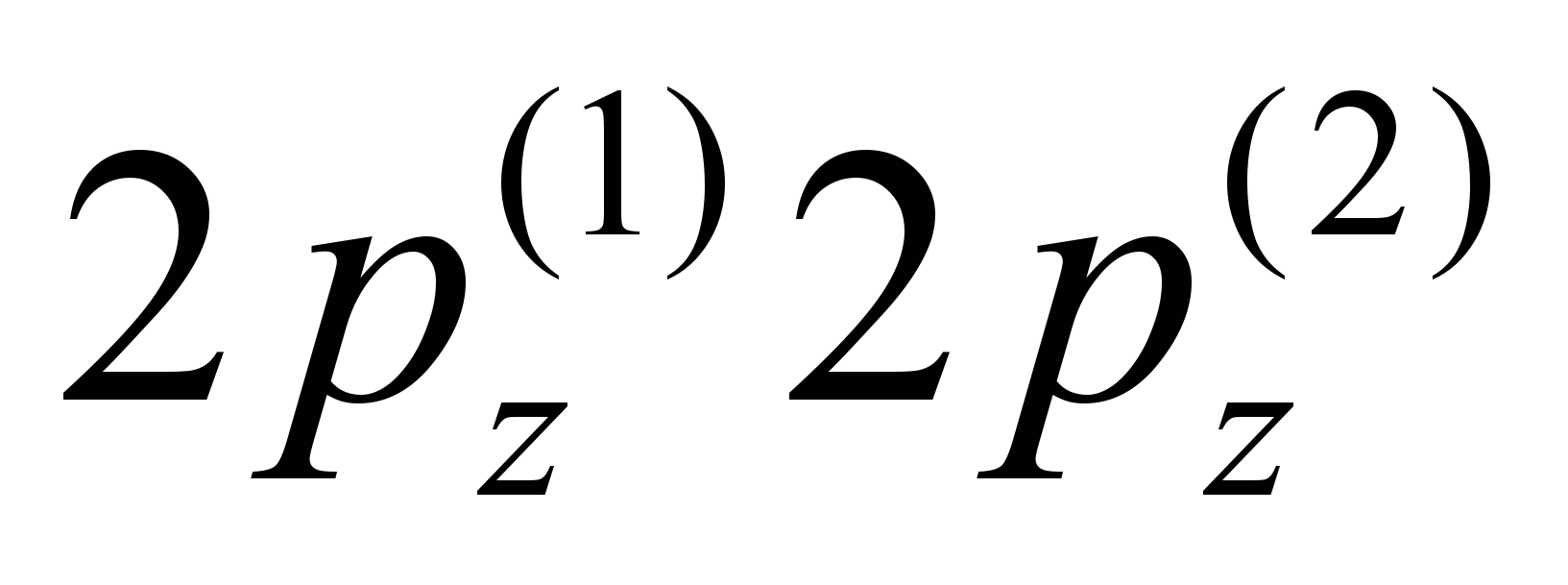((1) и (2) – номера атомов углерода в этилене):

Будем решать уравнение:



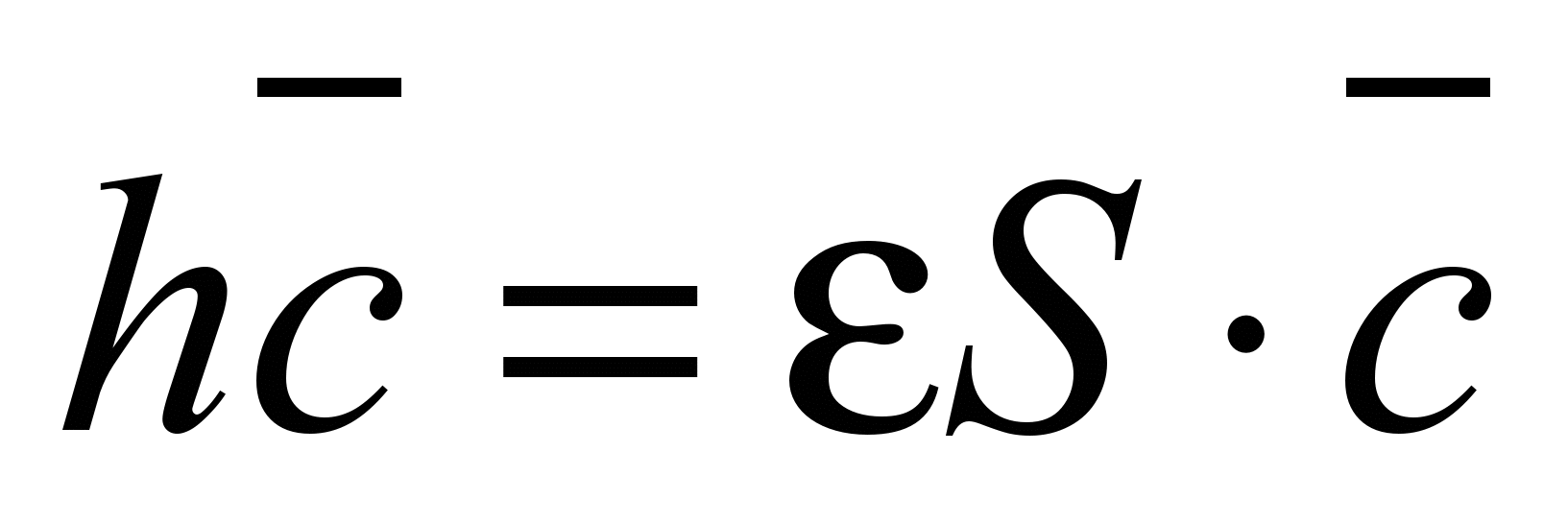
S=I (единичная матрица) – орбитали слабо перекрываются.







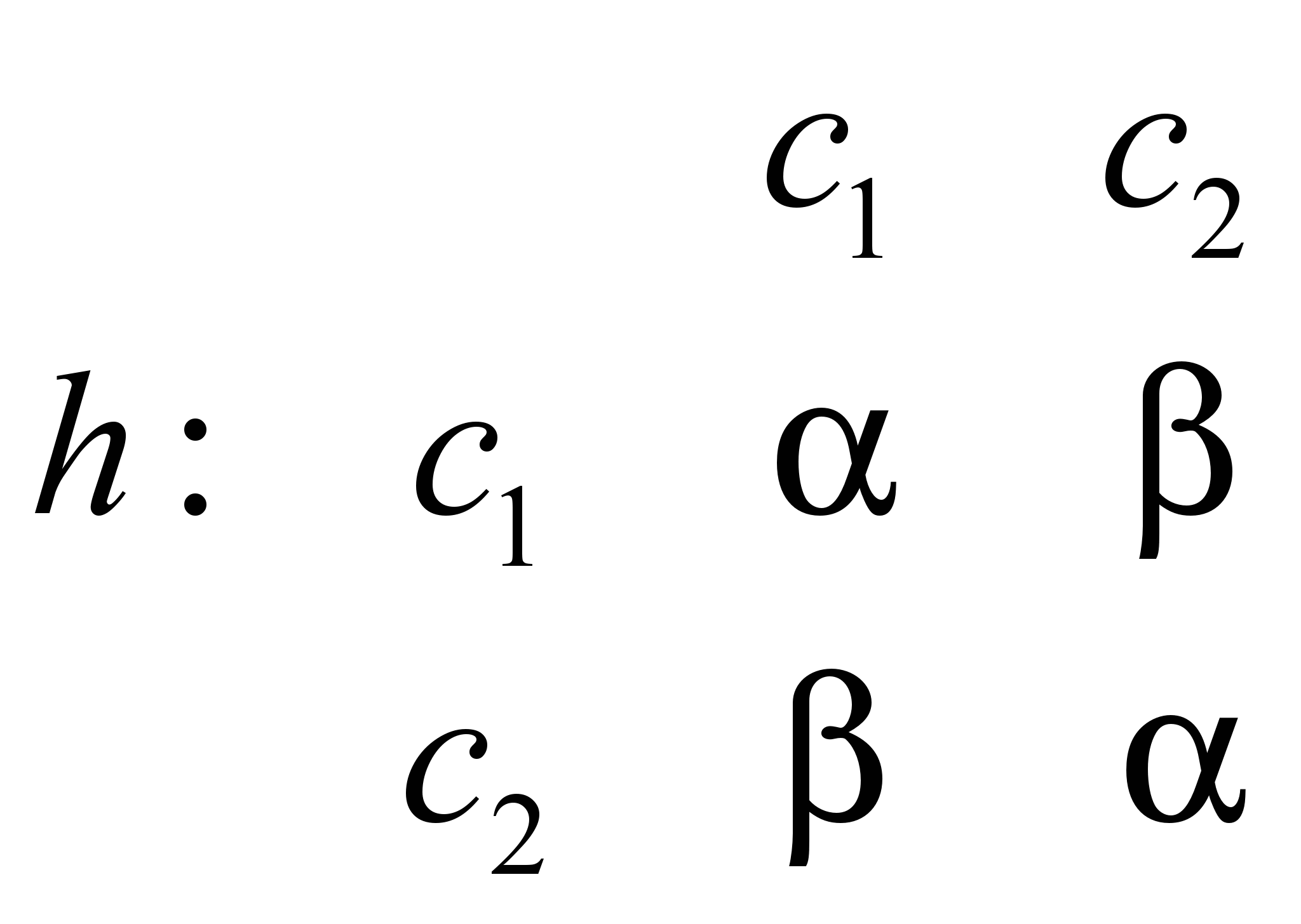
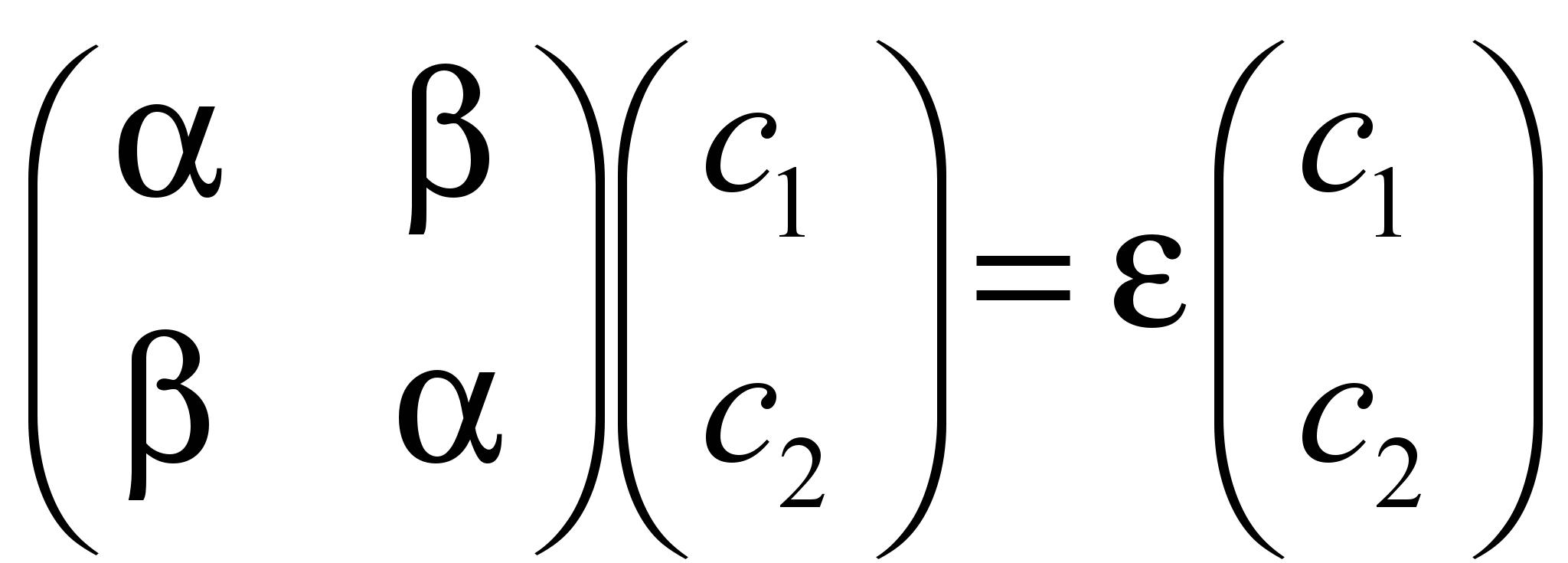
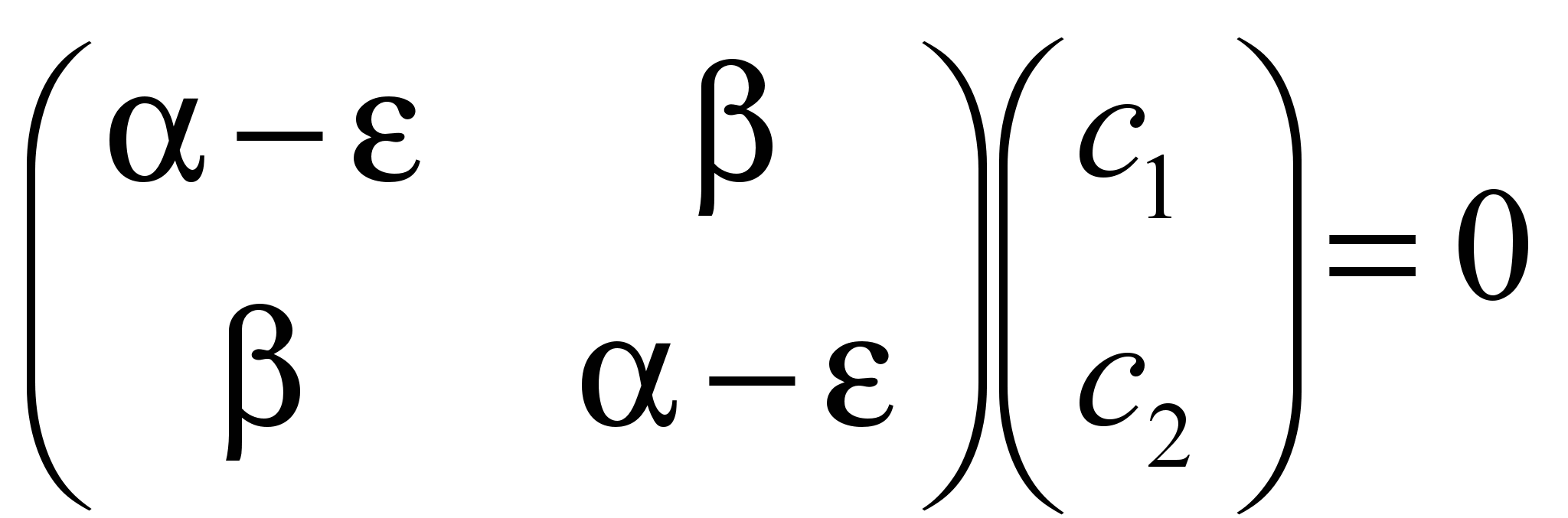
Чтобы у системы были ненулевые решения  .

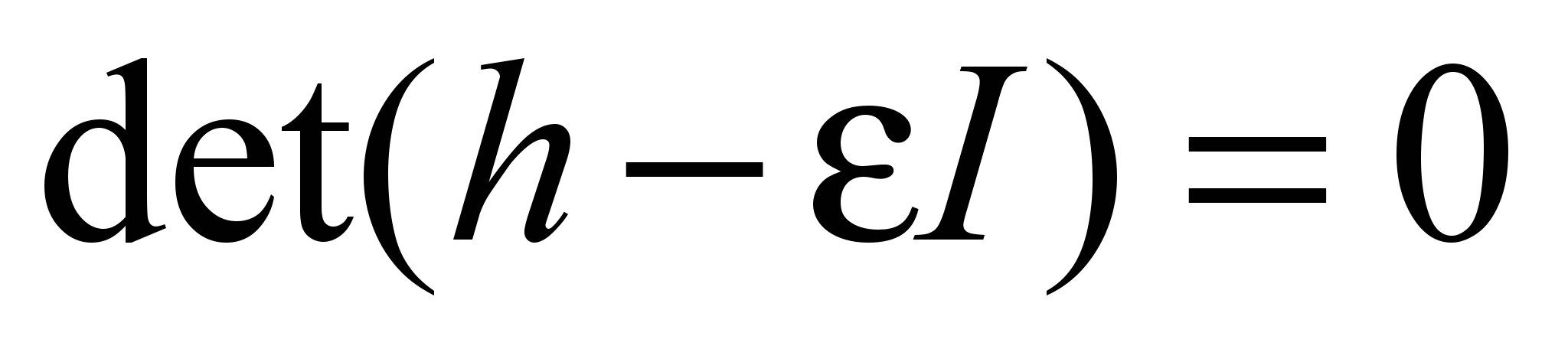Распишем :







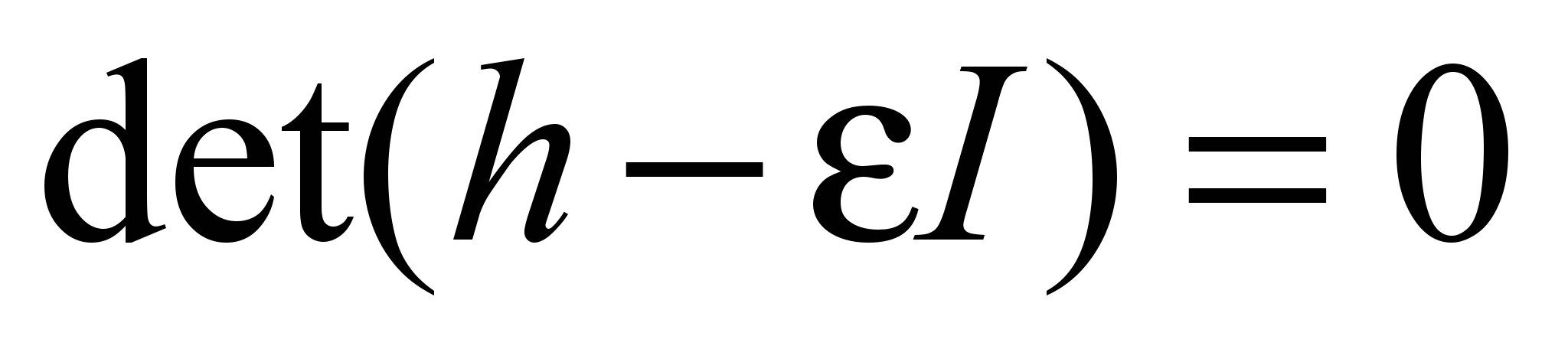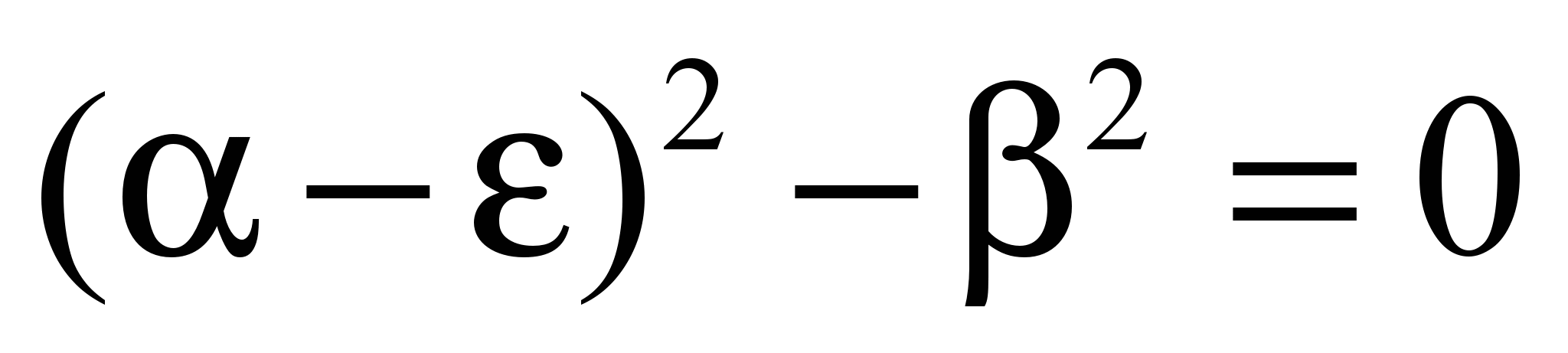
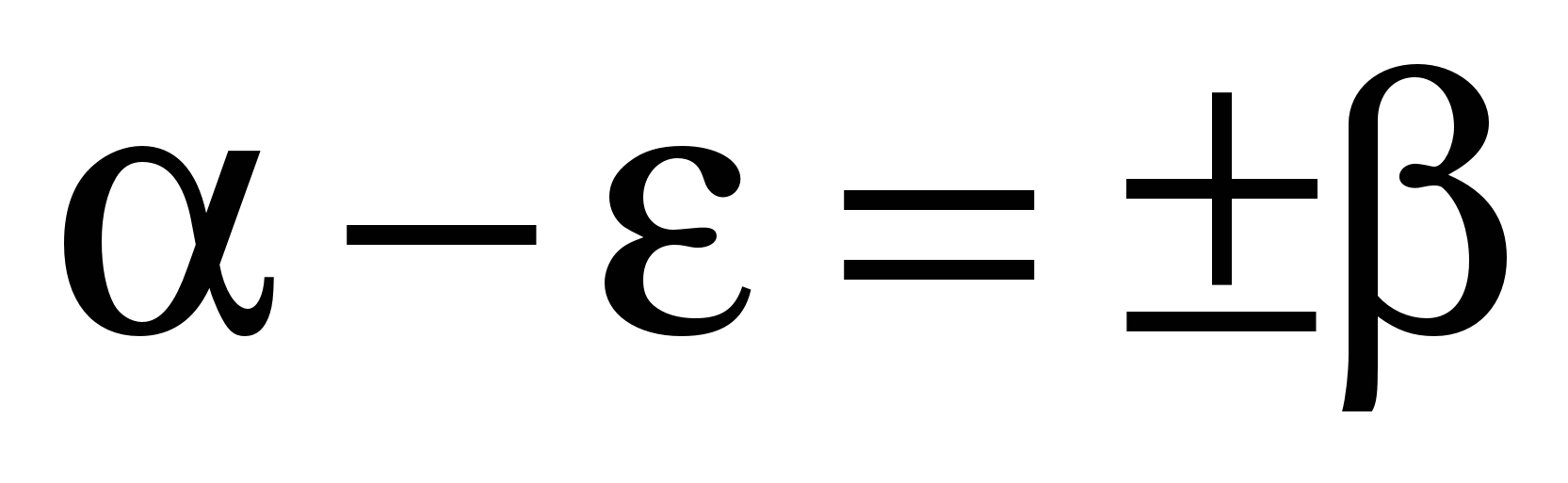
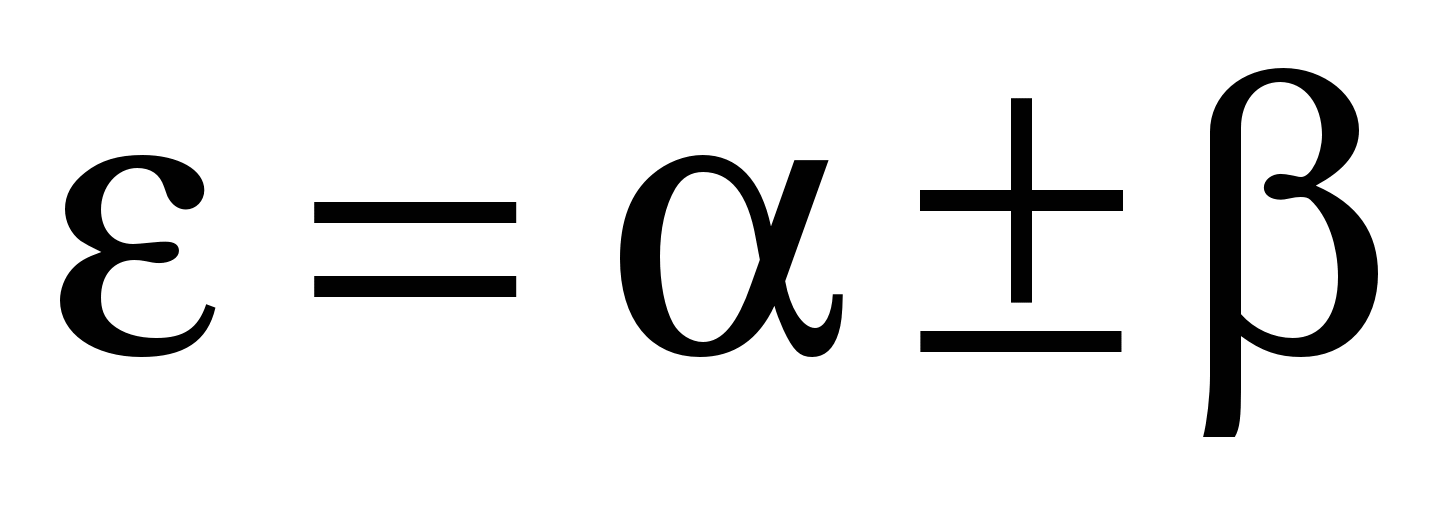
Подставим ε₁=α+β в уравнение :







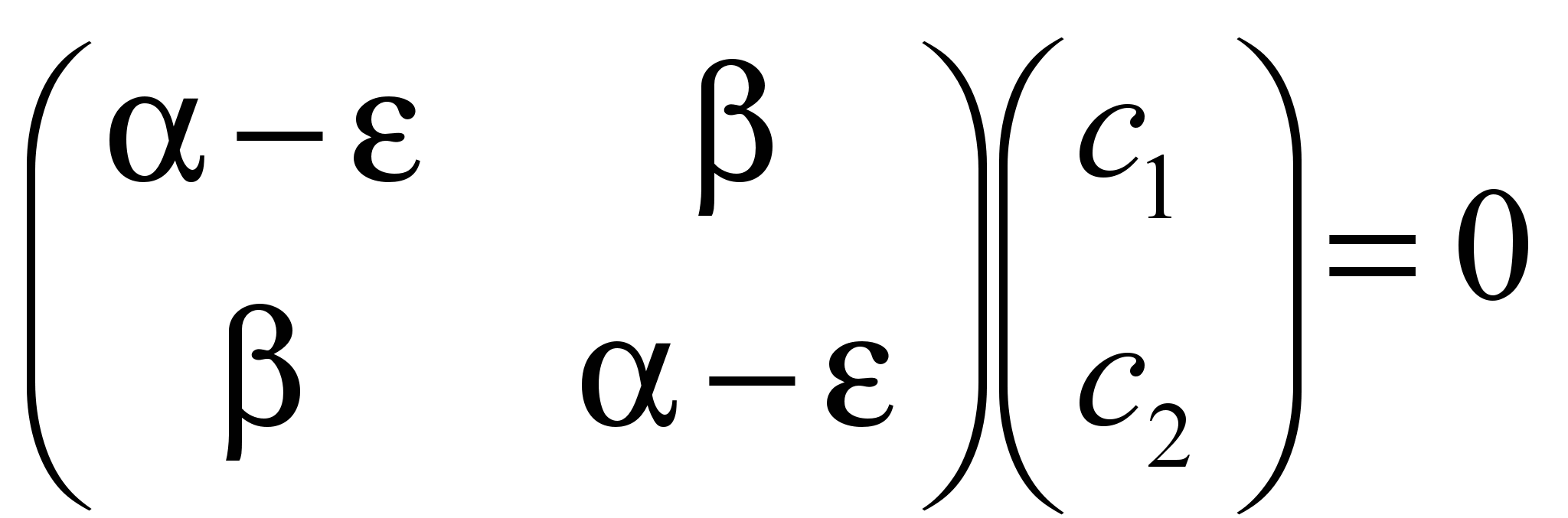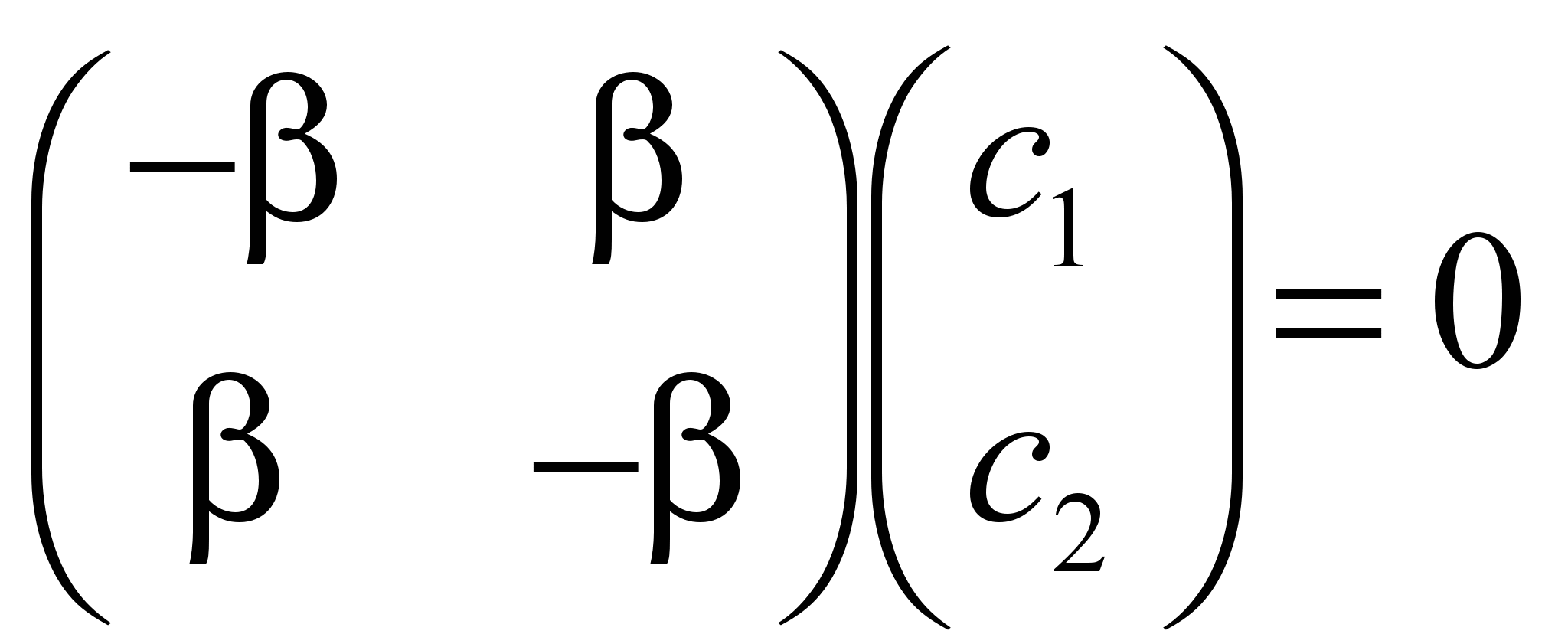
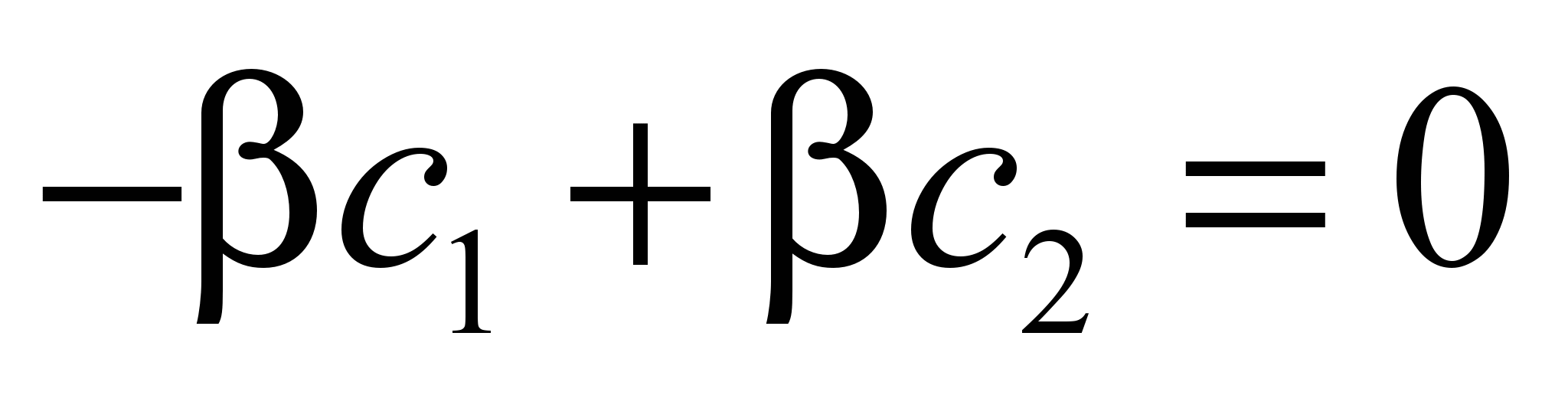
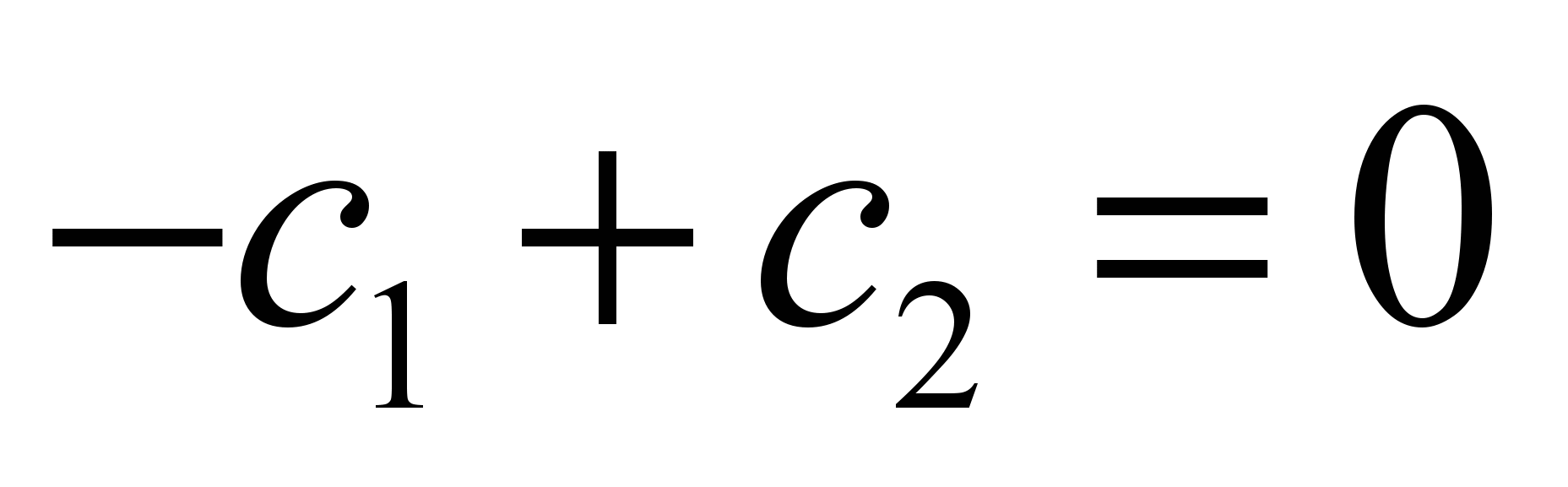
Отсюда следует, что с₁=с₂. Следовательно:



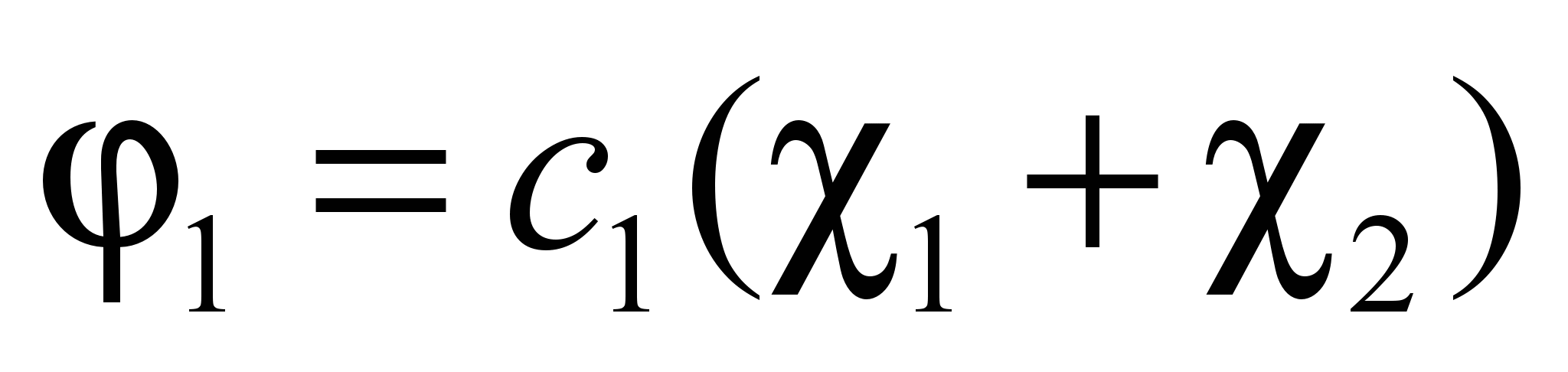
С учетом нормировки:



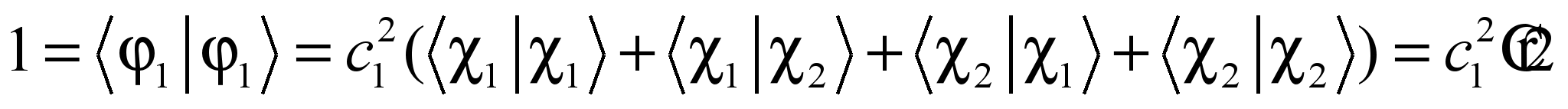
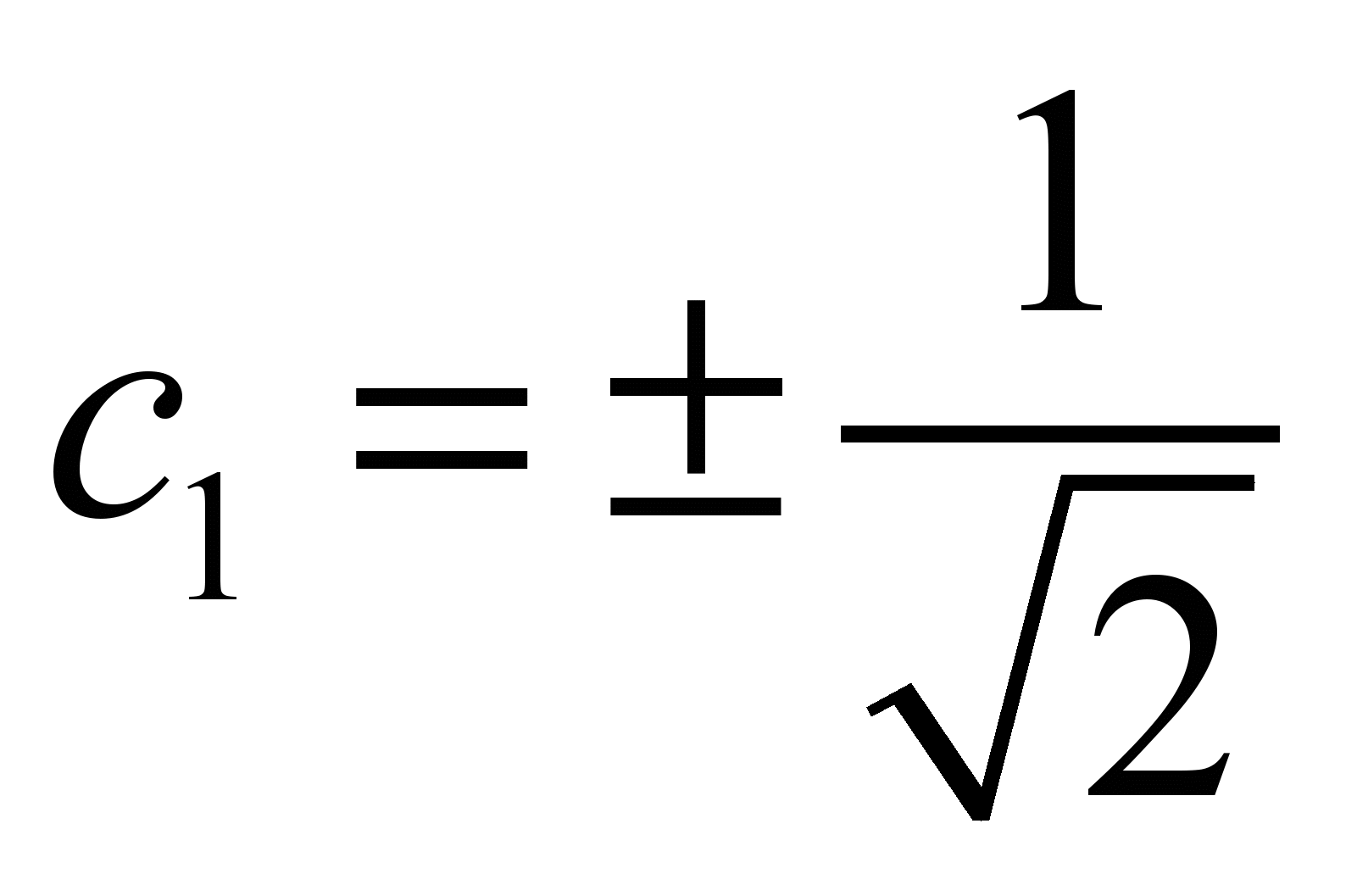, т.е.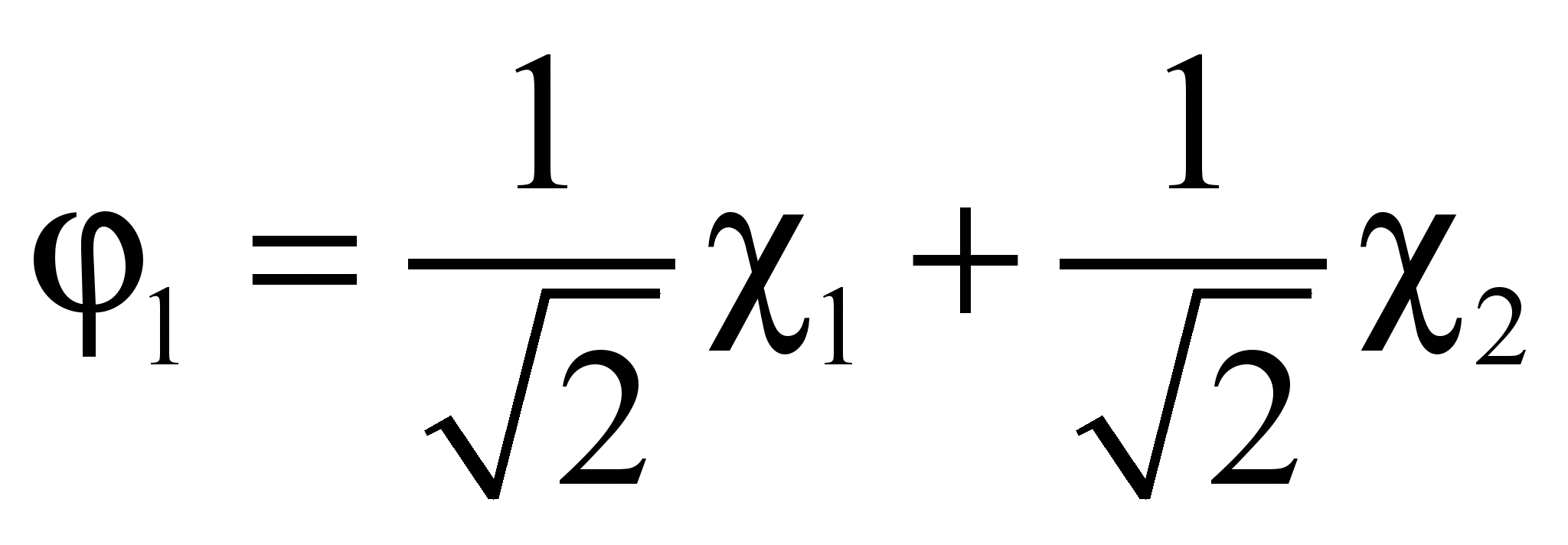



Подставим ε₂=α-β в уравнение:









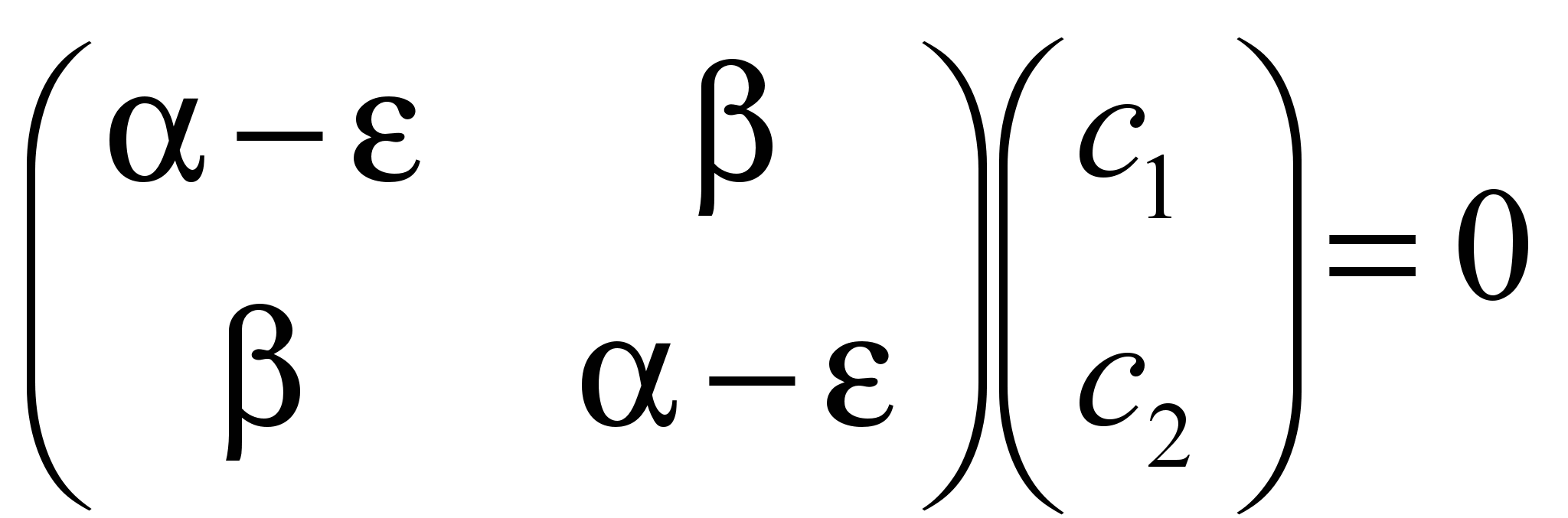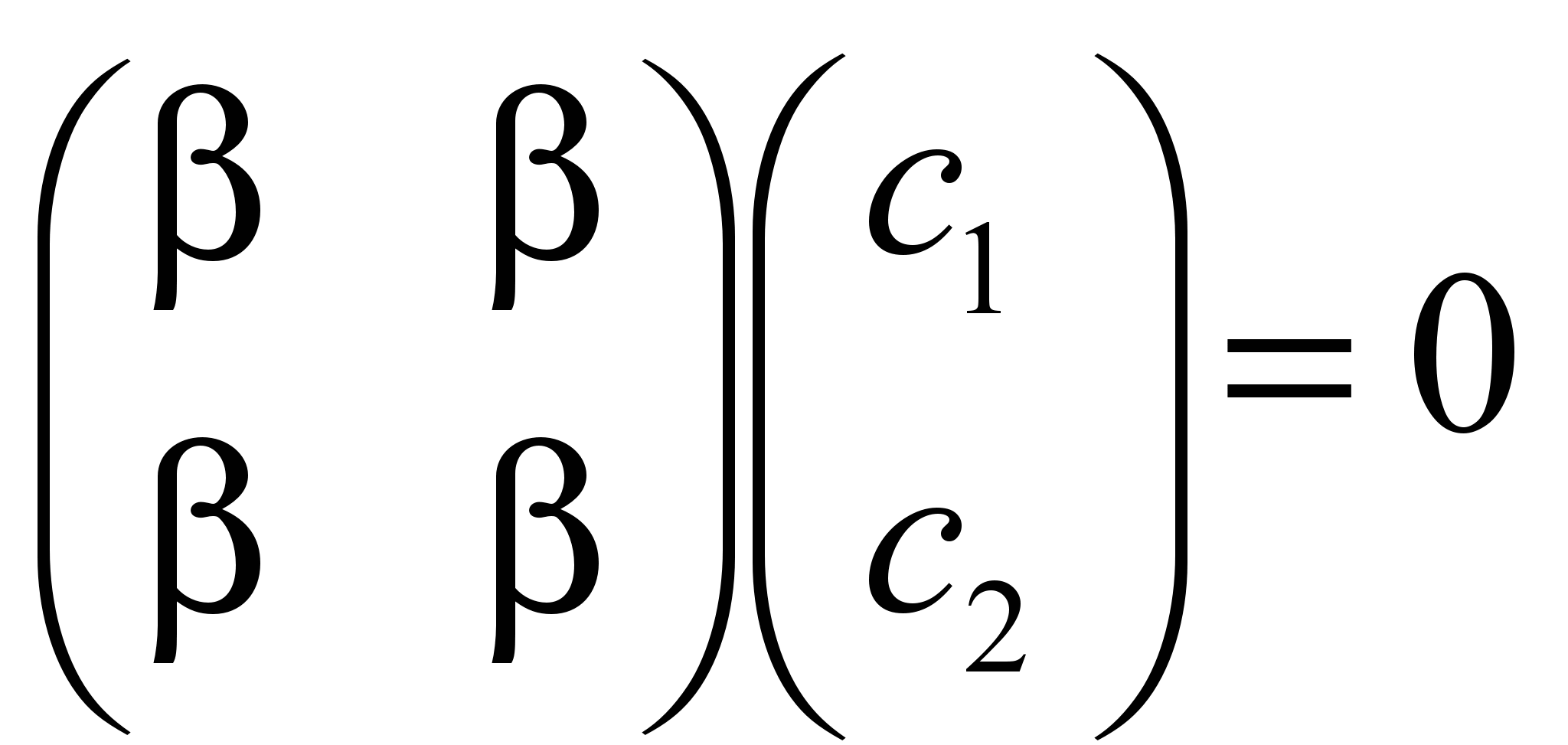
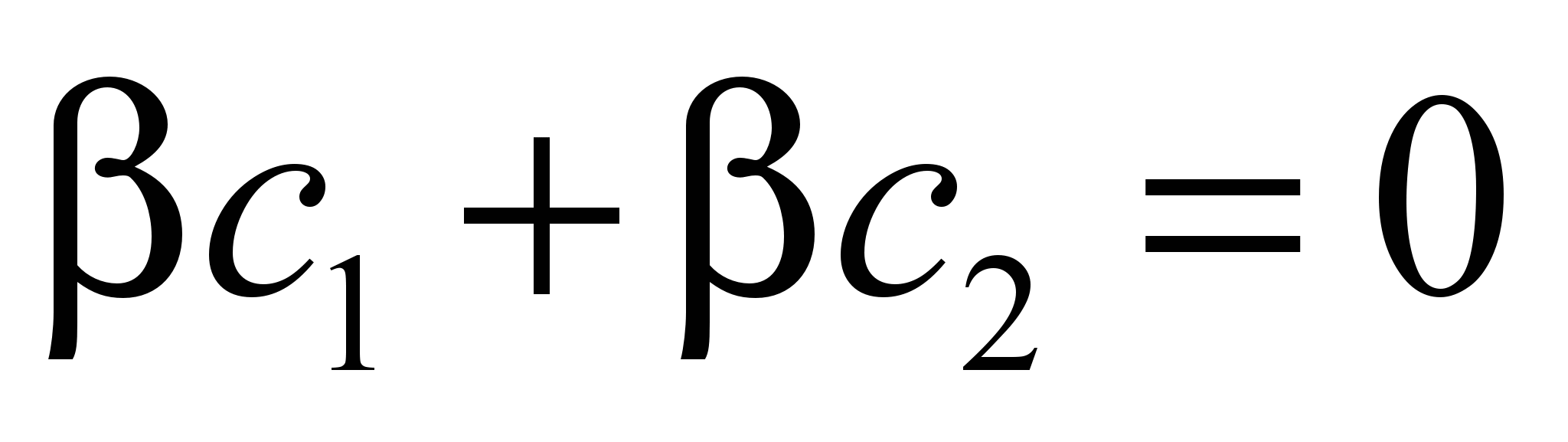
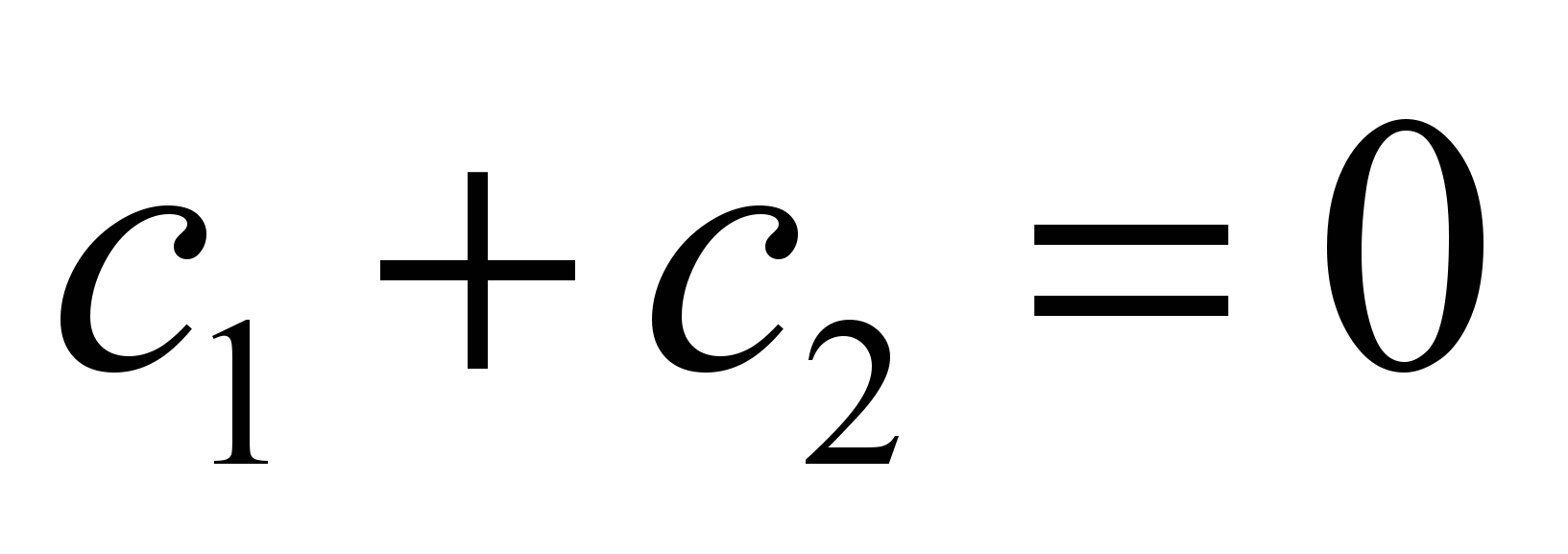
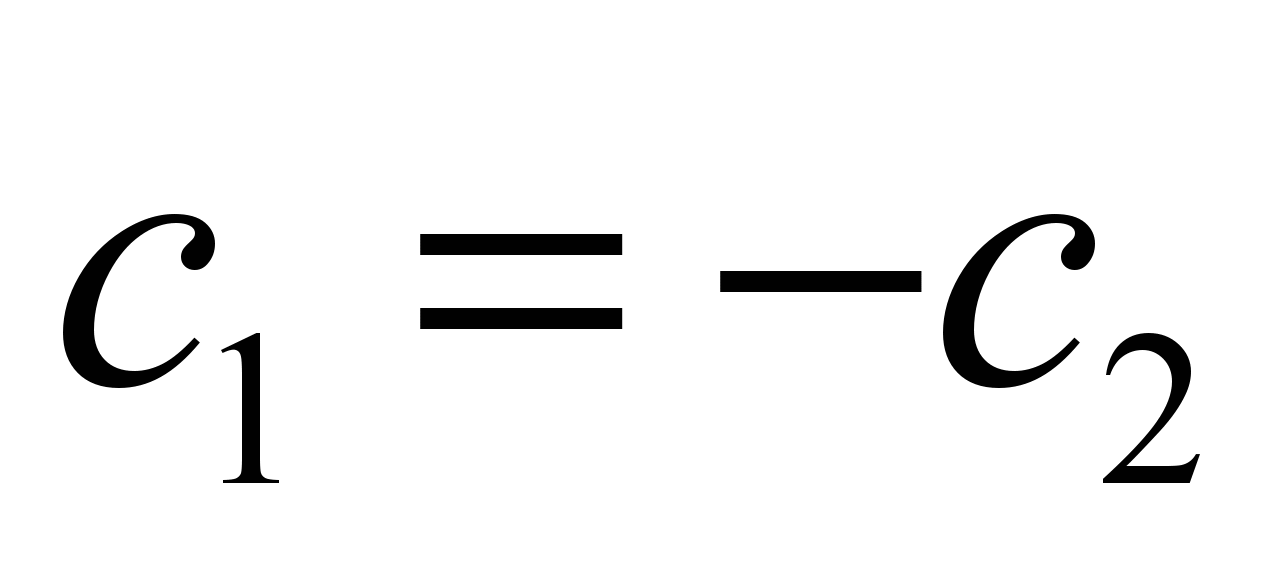
С учетом нормировки:









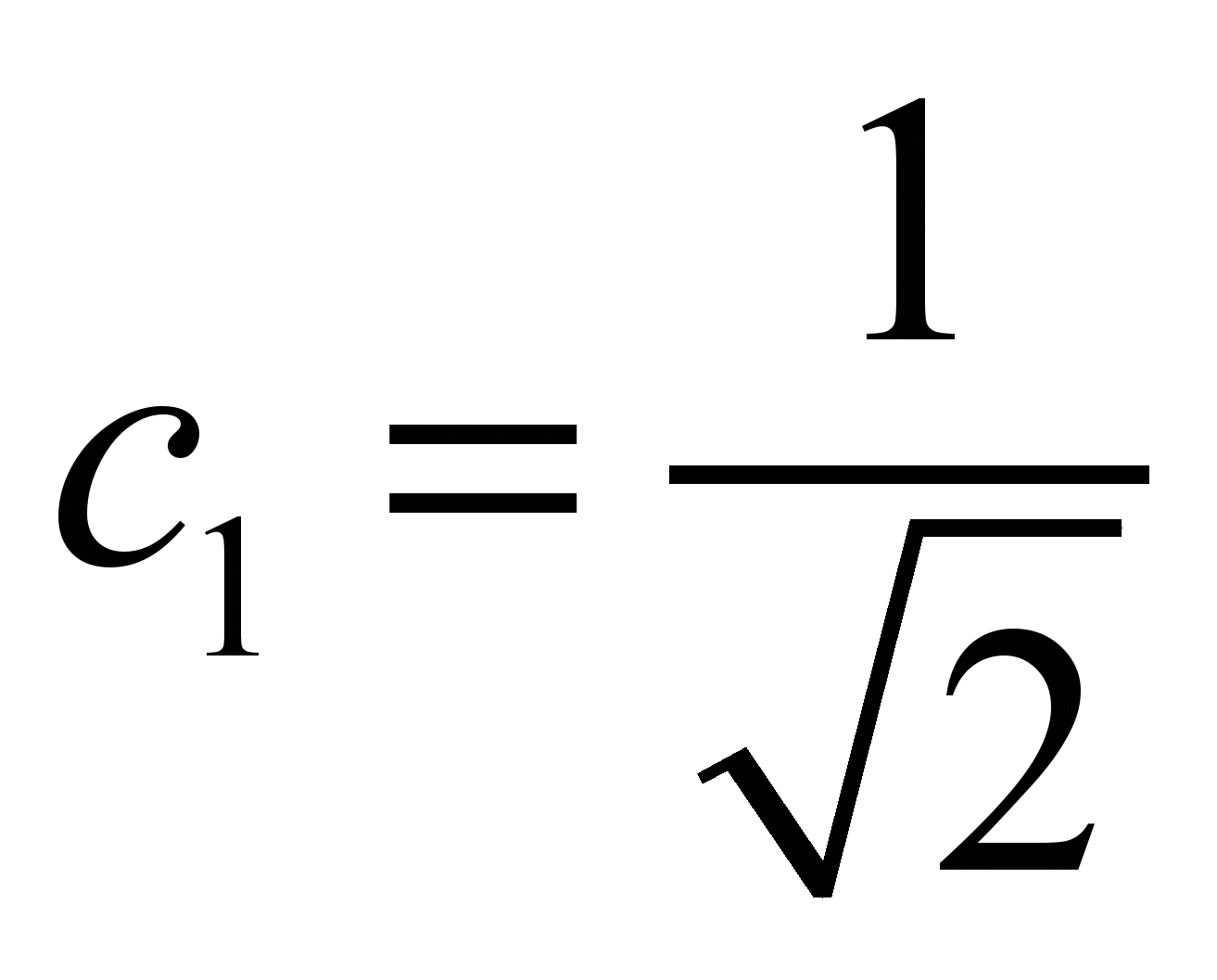
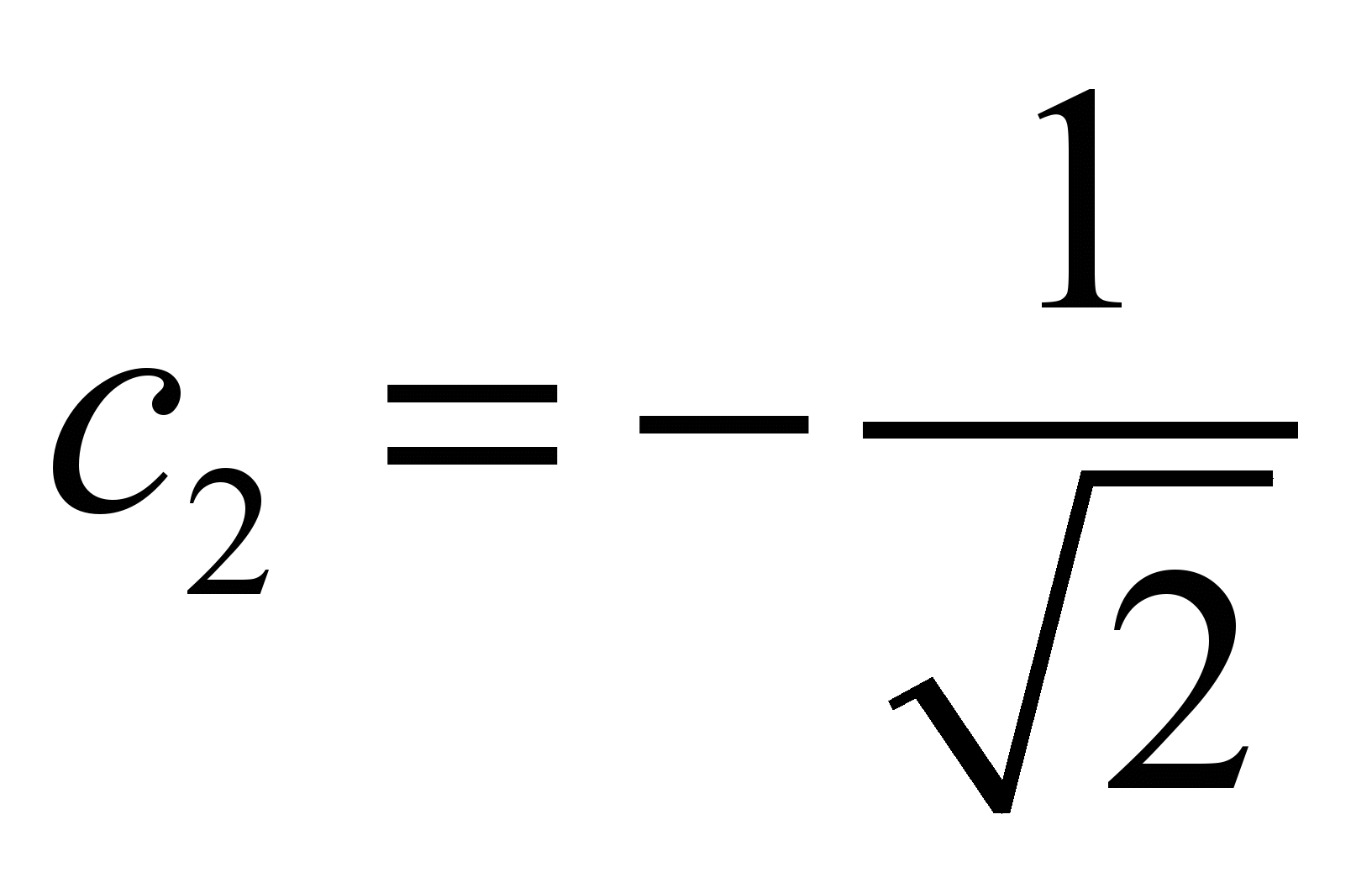
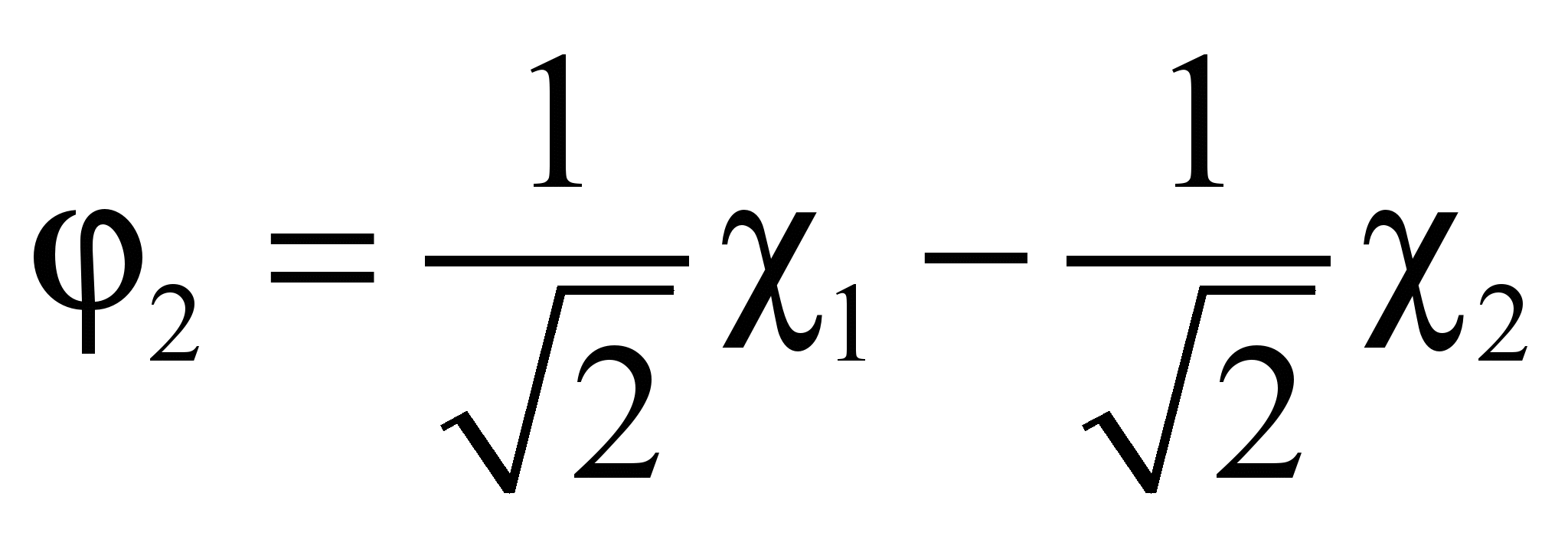
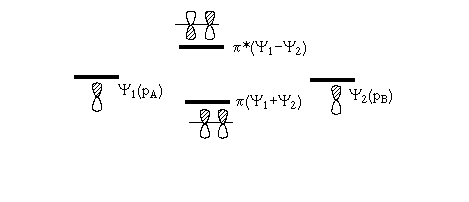
А теперь рассмотрим аллил-радикал:







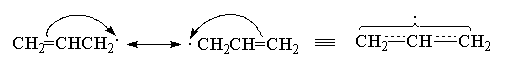
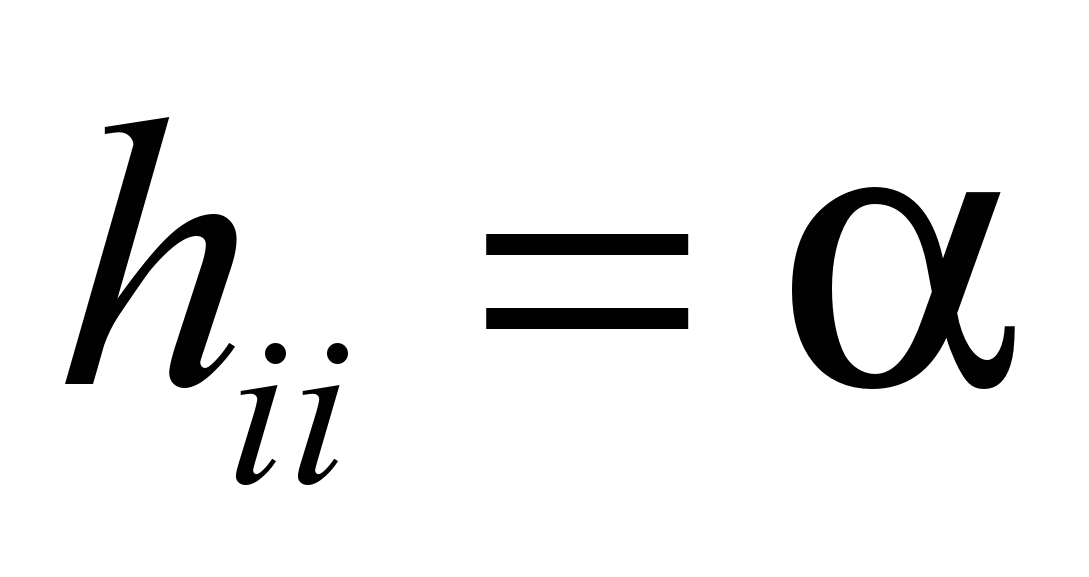
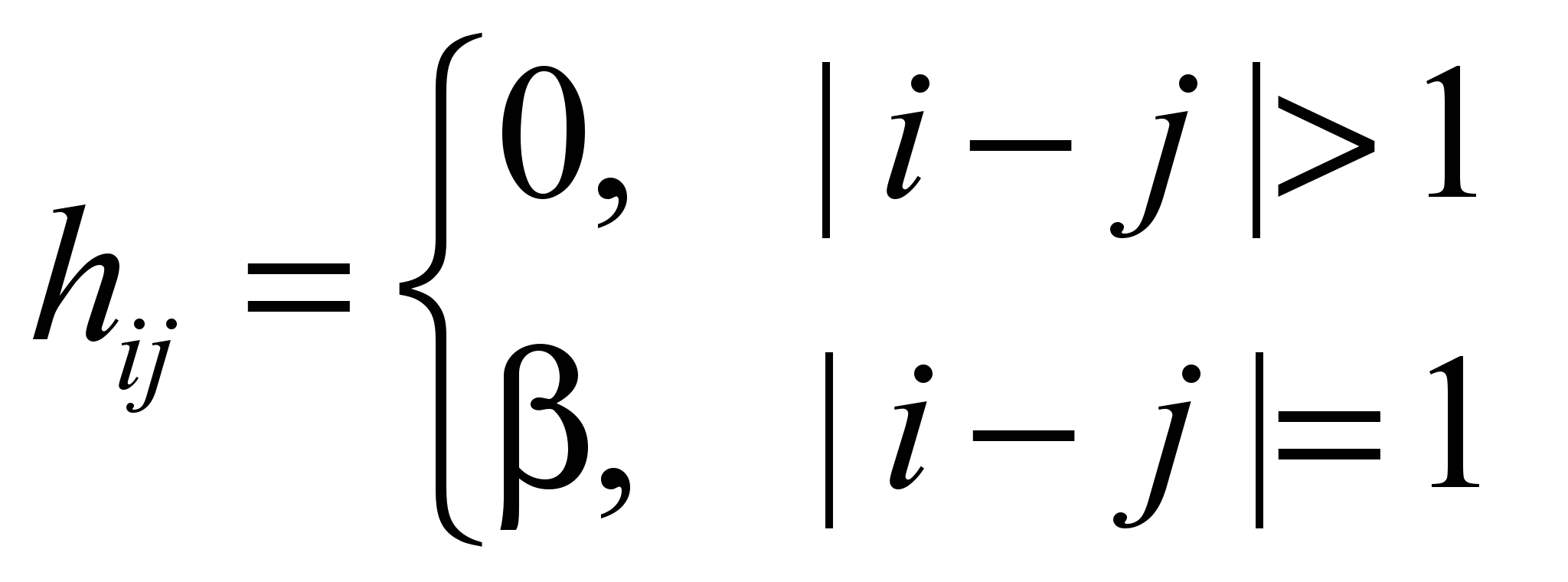
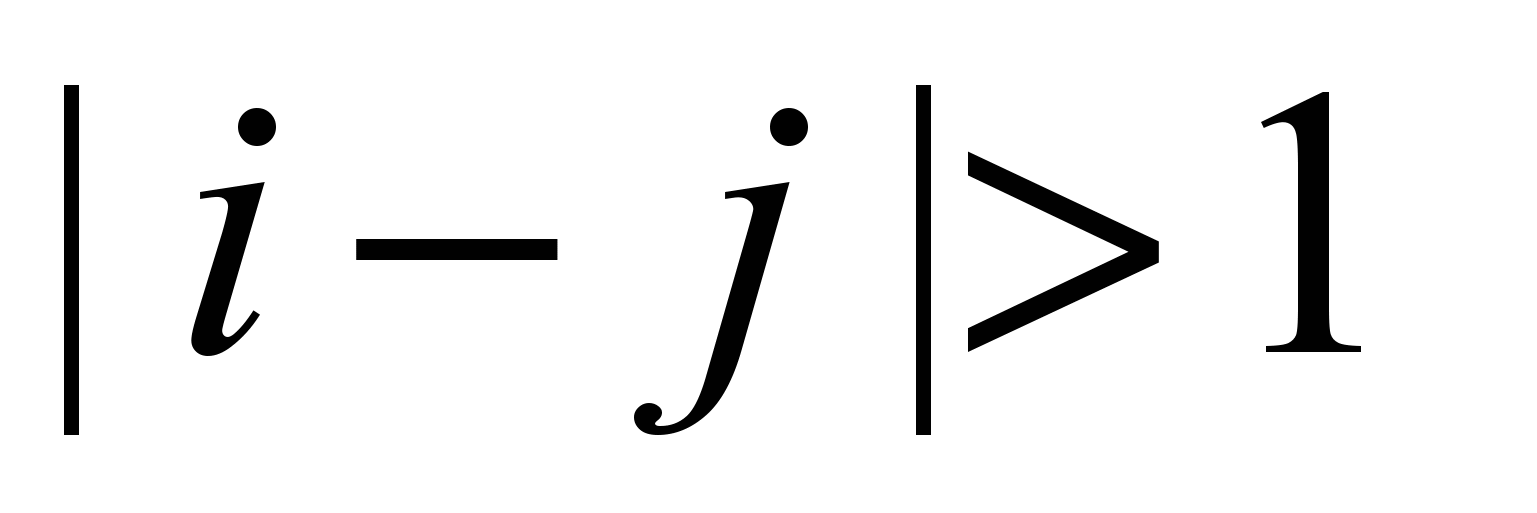- отсутствие связи, 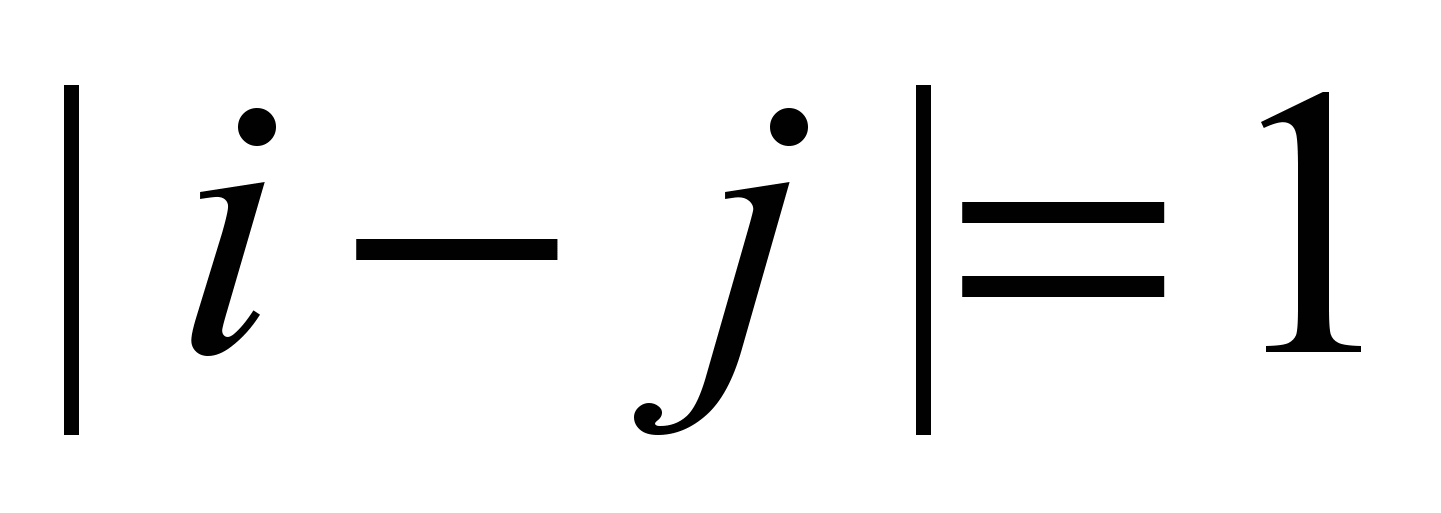- соседние атомы.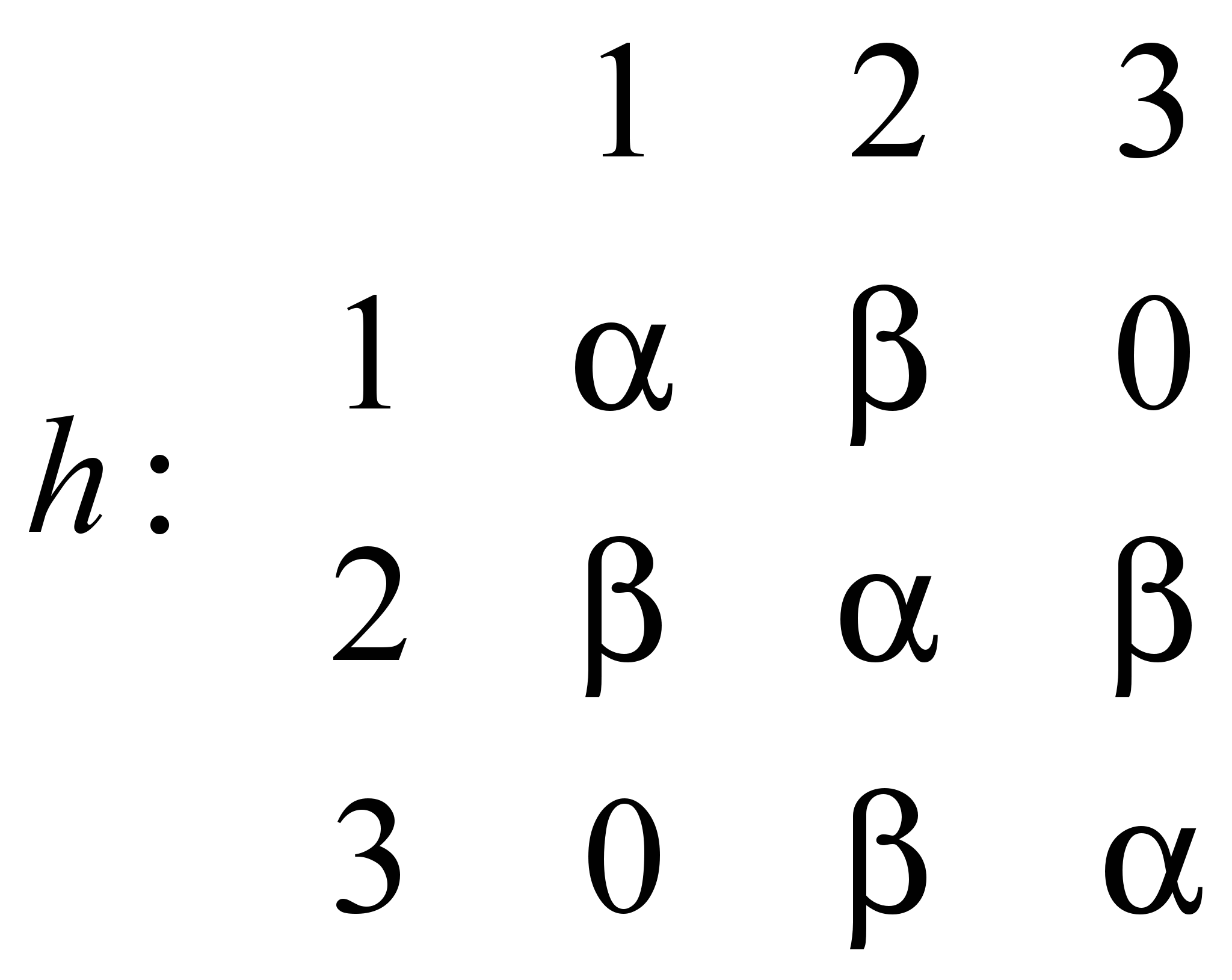



Необходимое условие существования ненулевых решений  .

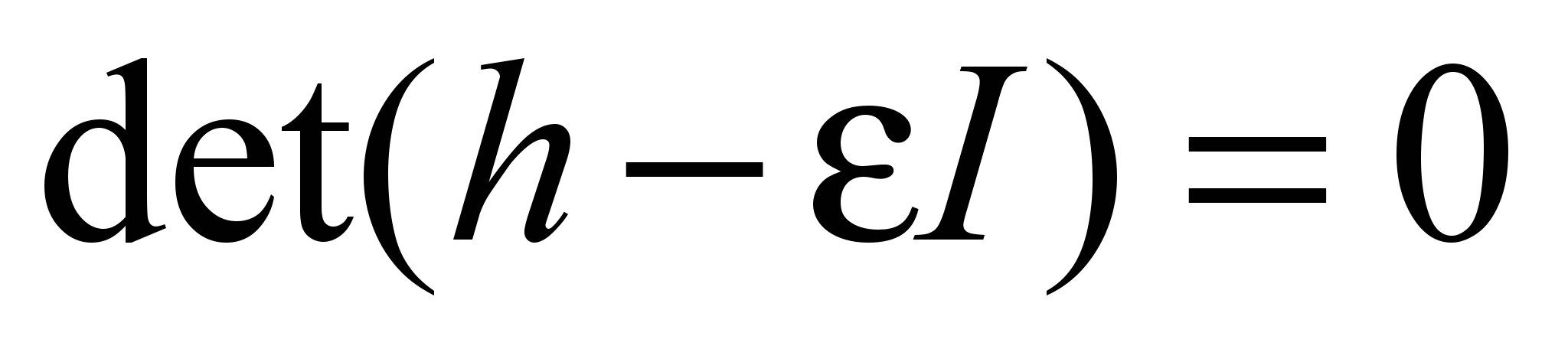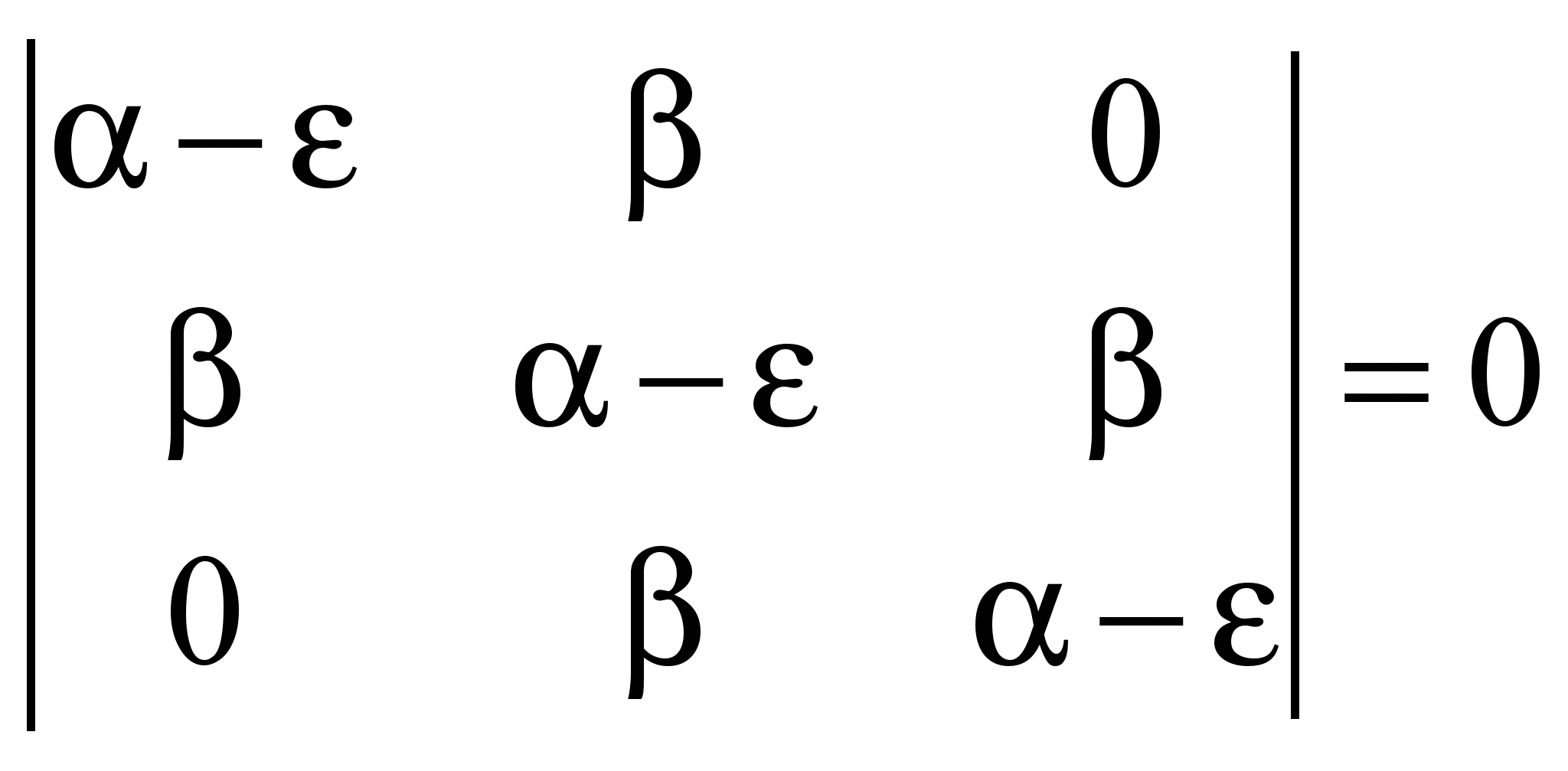, произведем замену: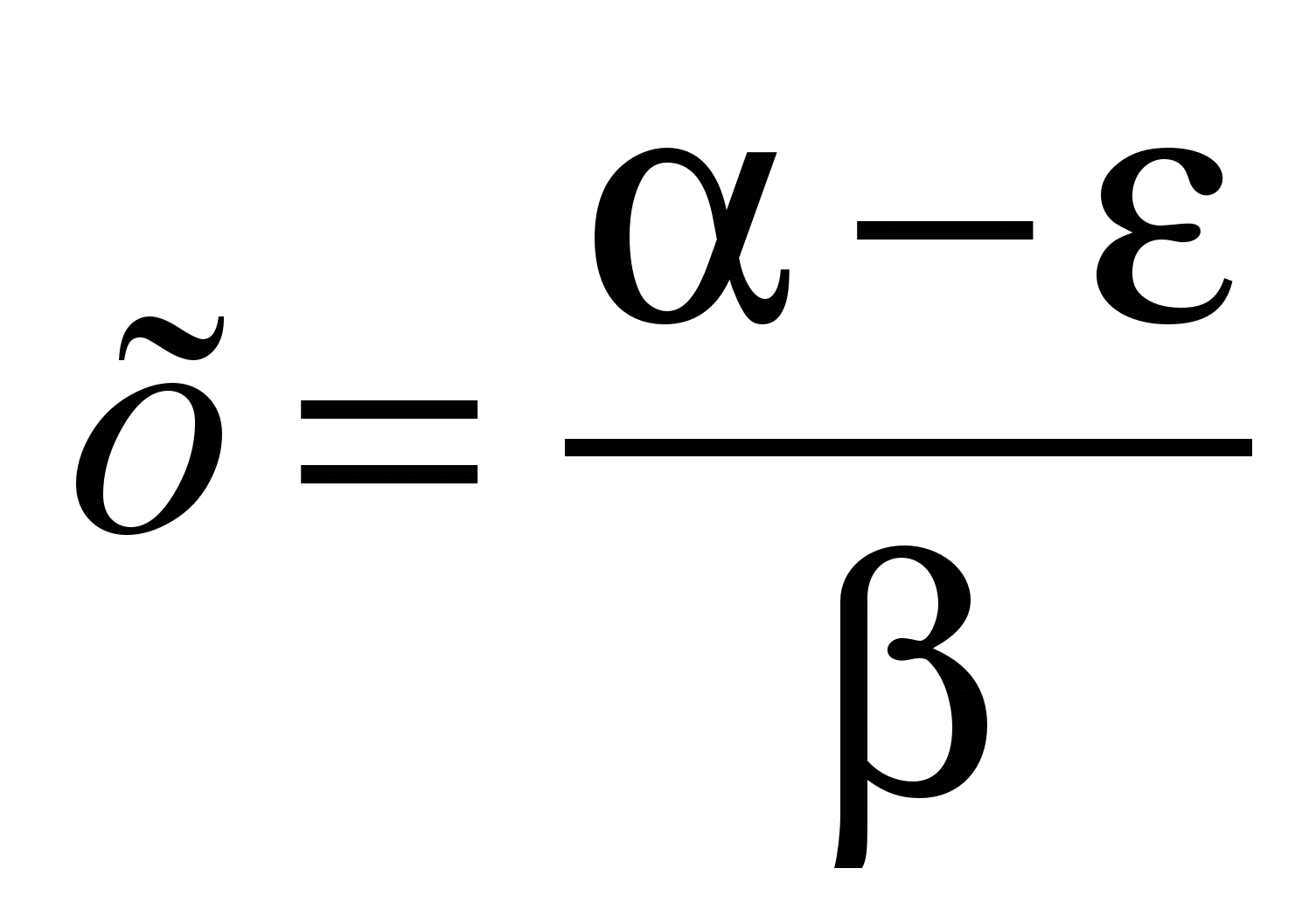

















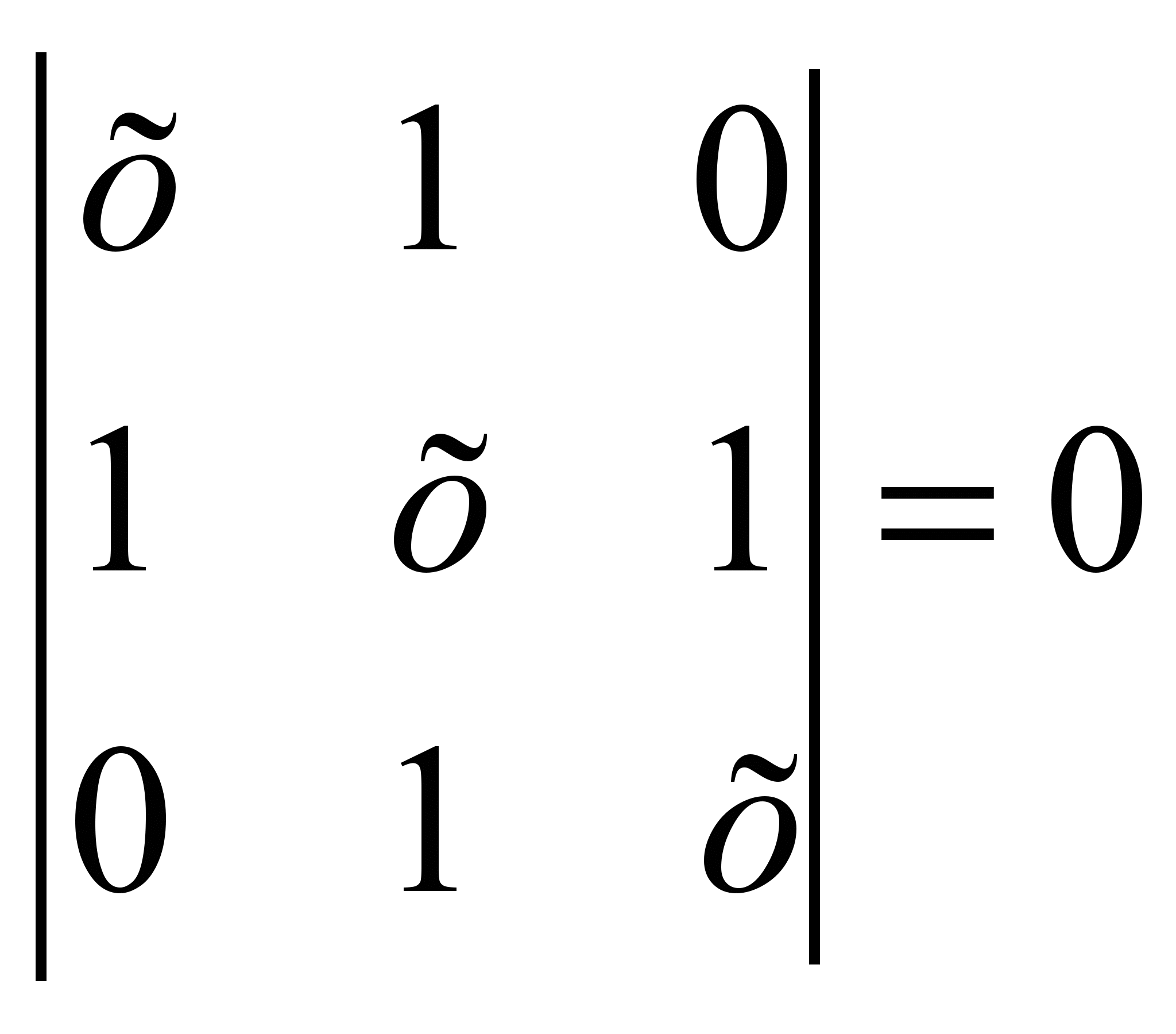
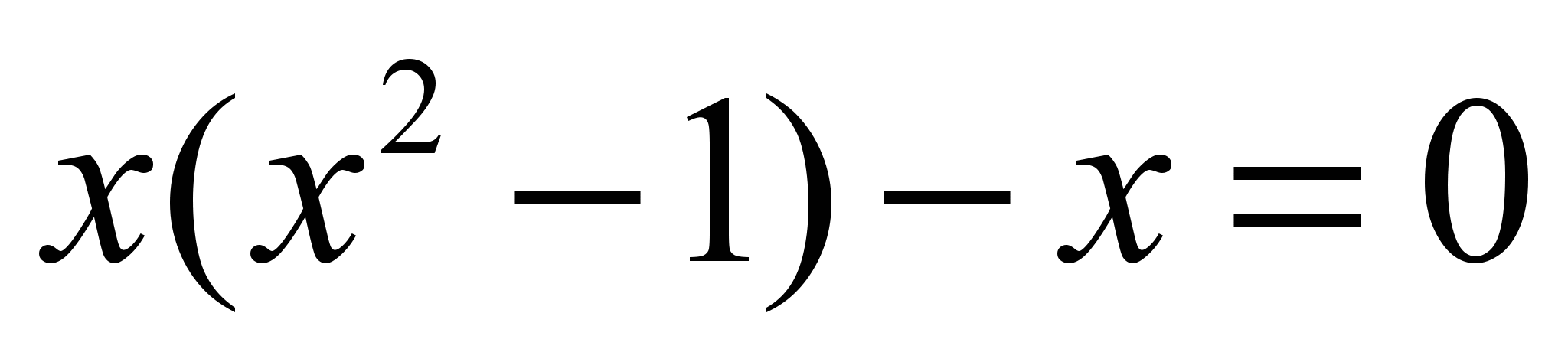
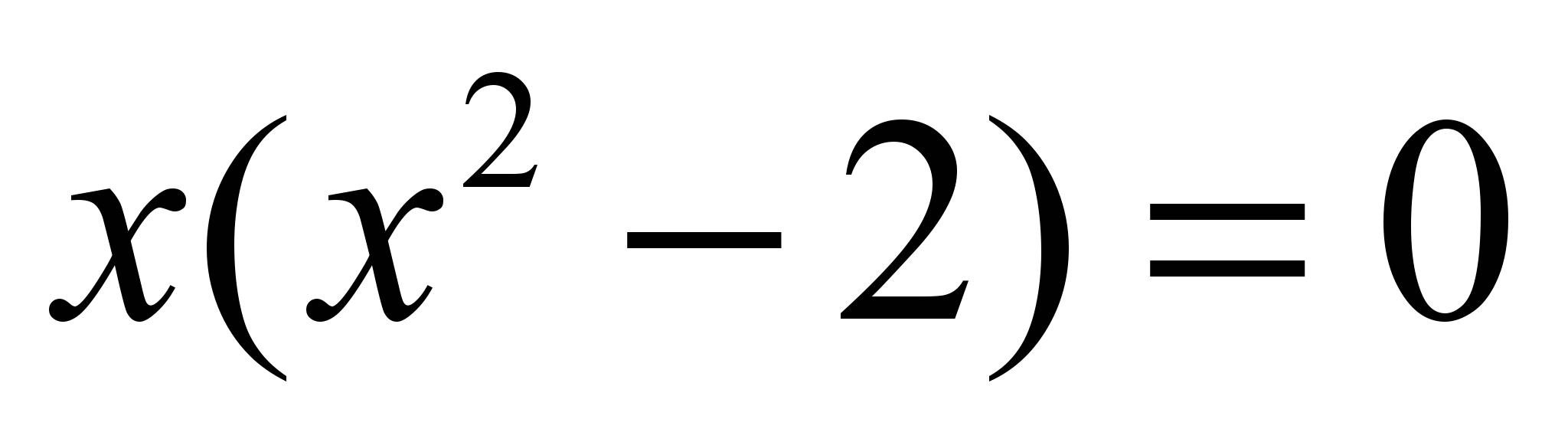
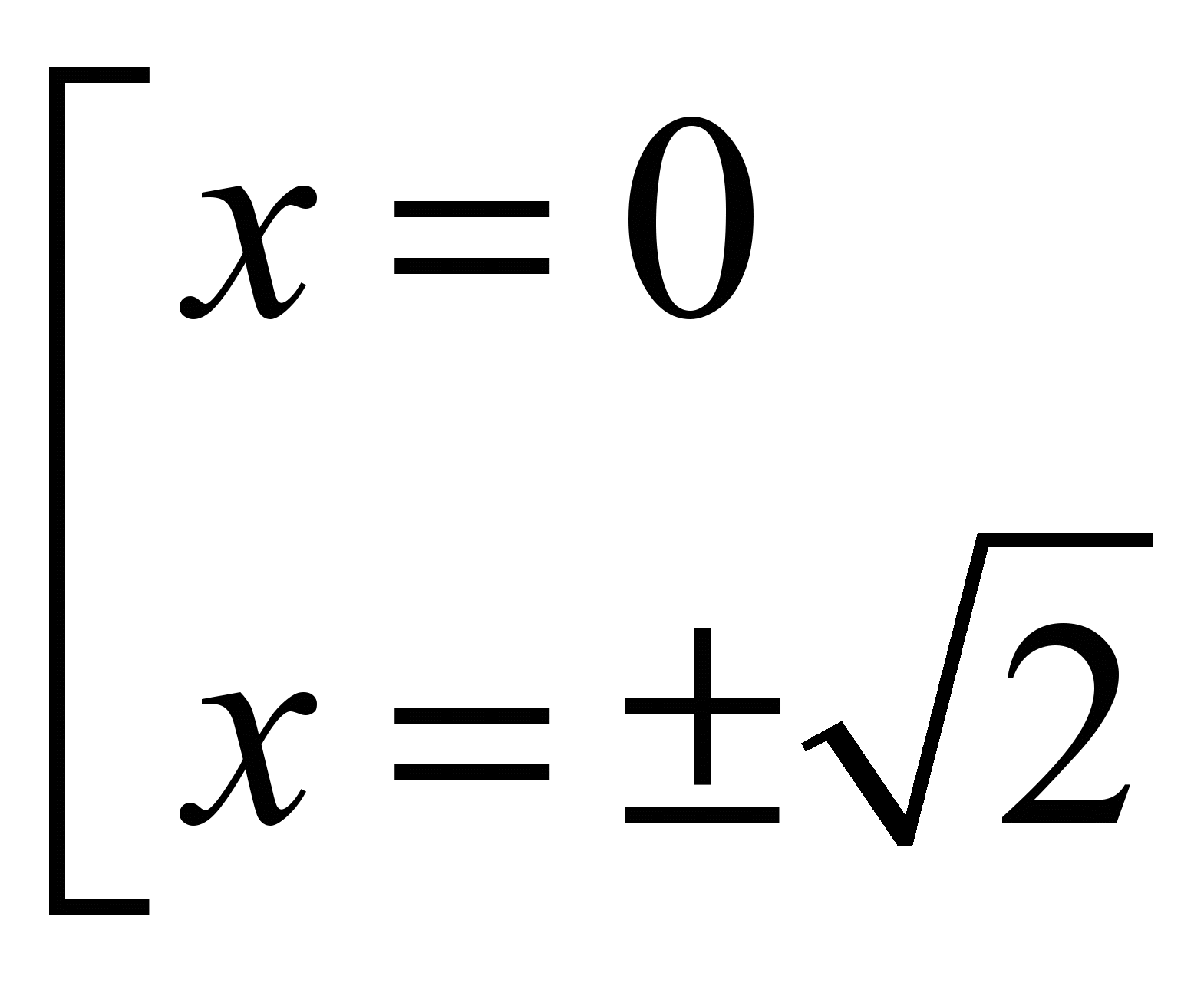
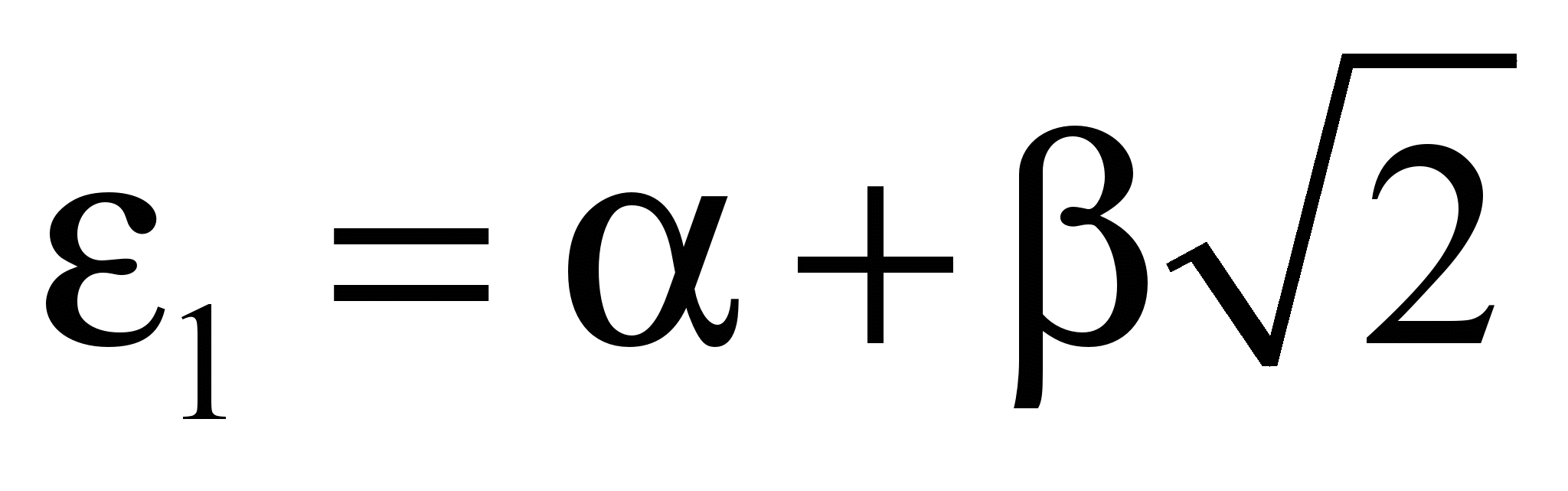
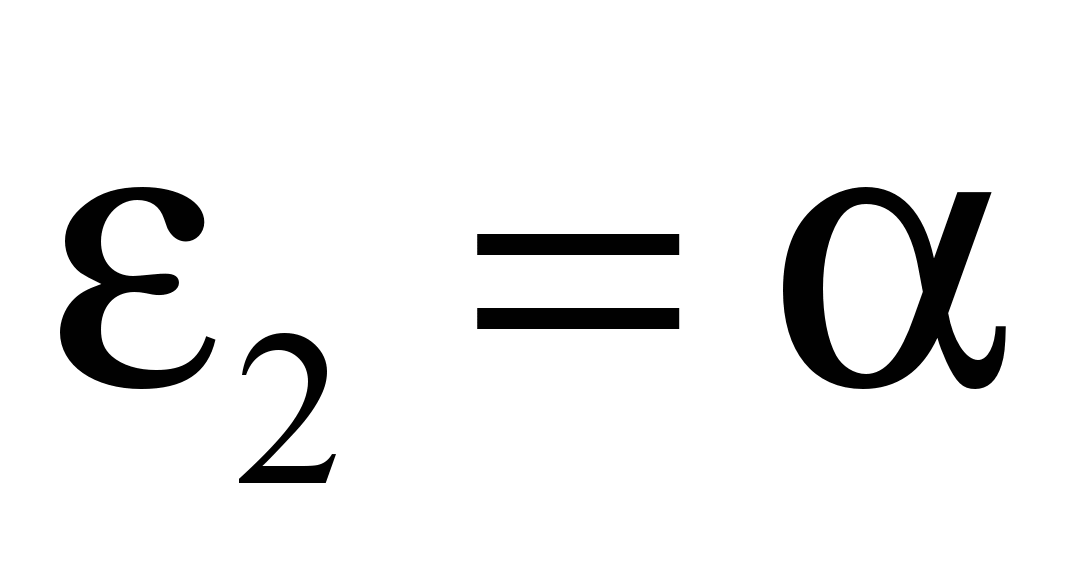
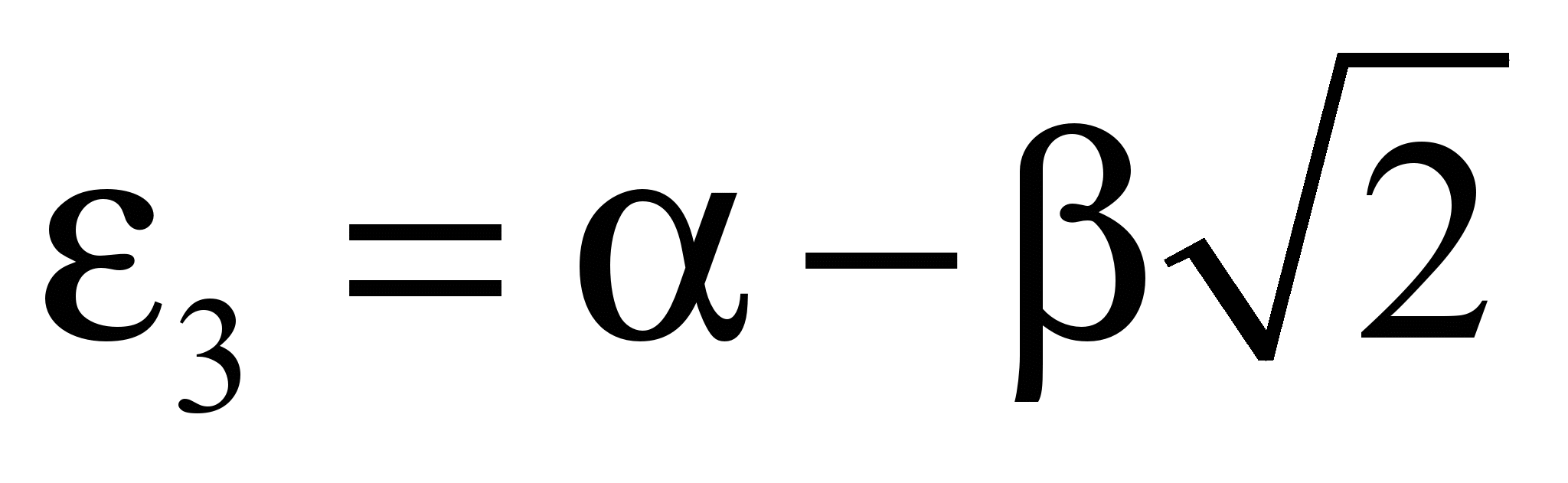
После элементарных алгебраических операций получим:

1. x=0:
   

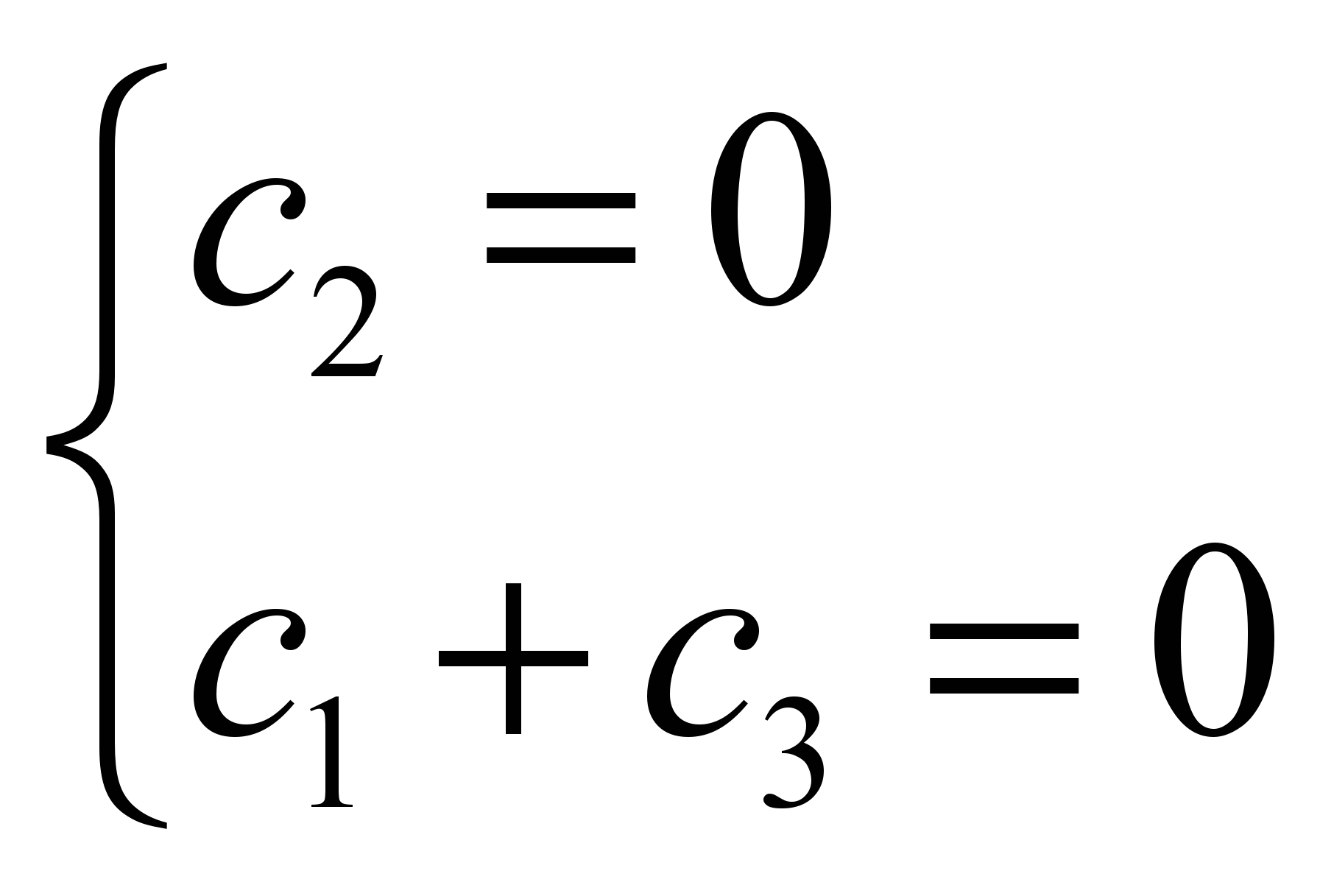
С учетом нормировки :

2. :
   

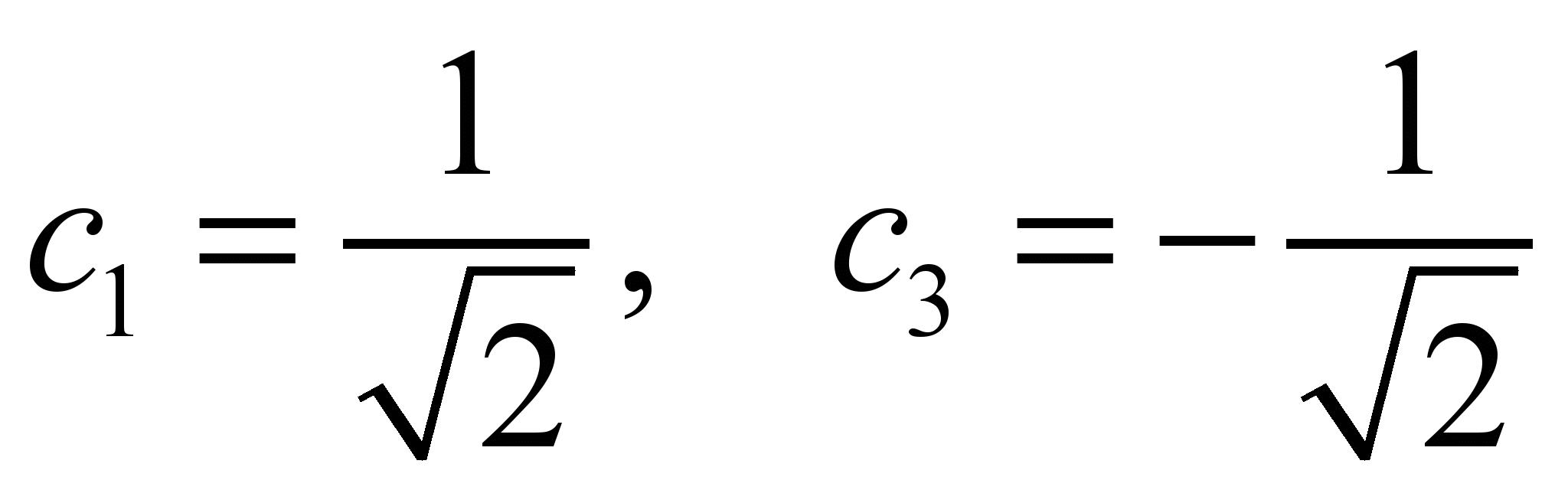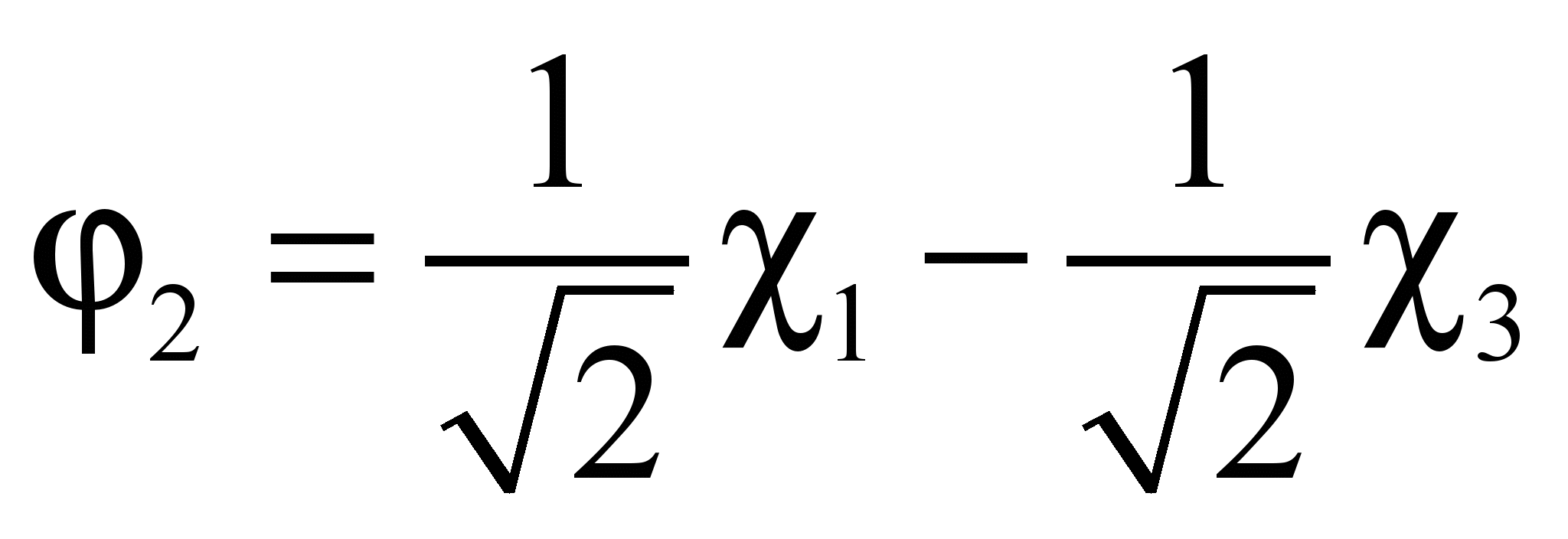
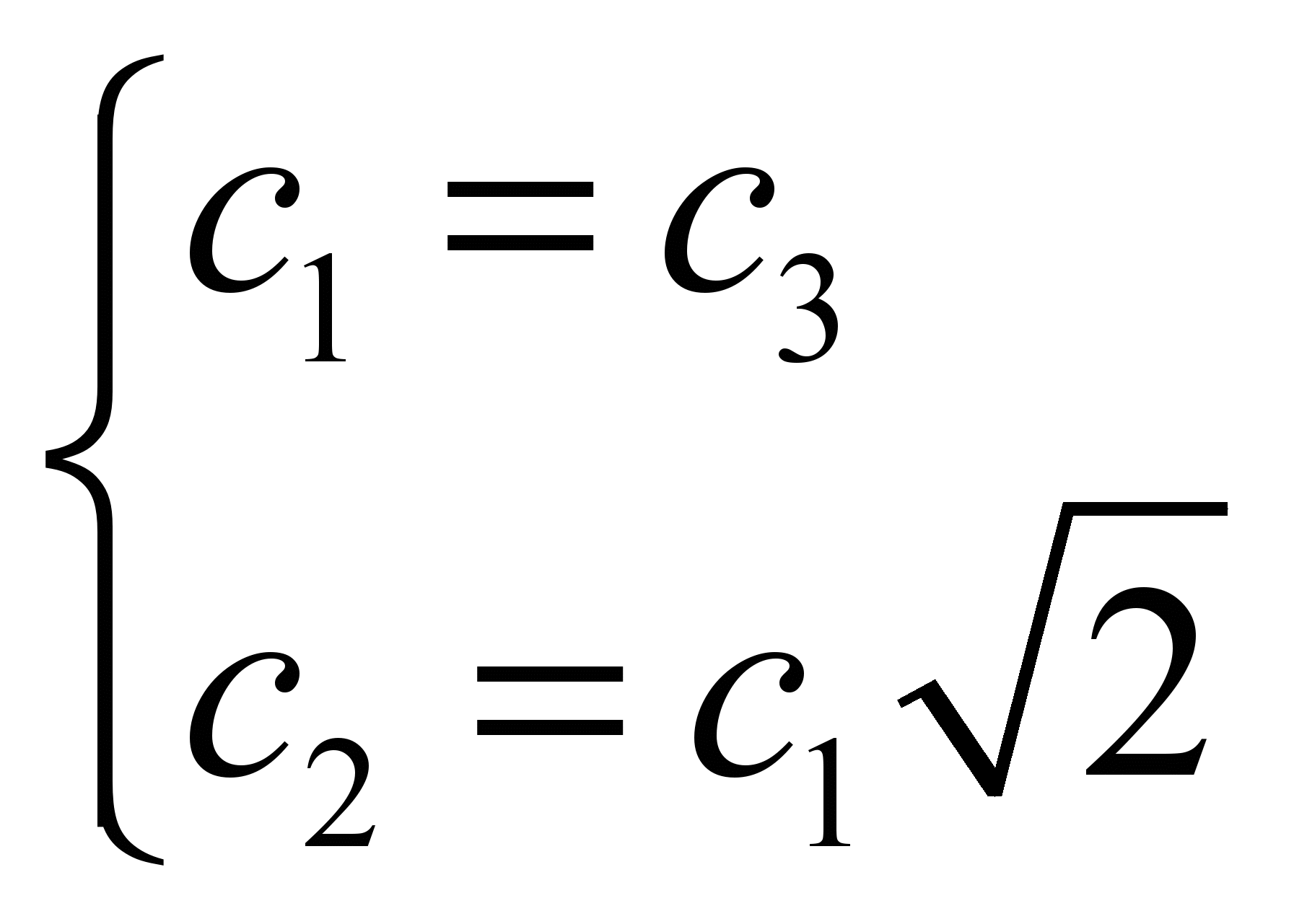
С учетом нормировки

3. :
   

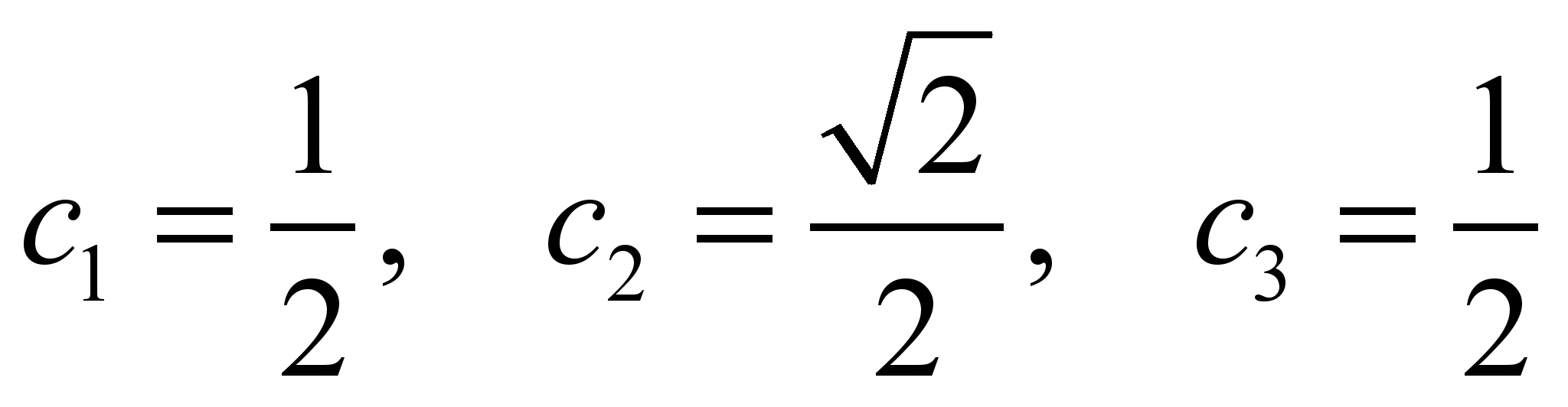
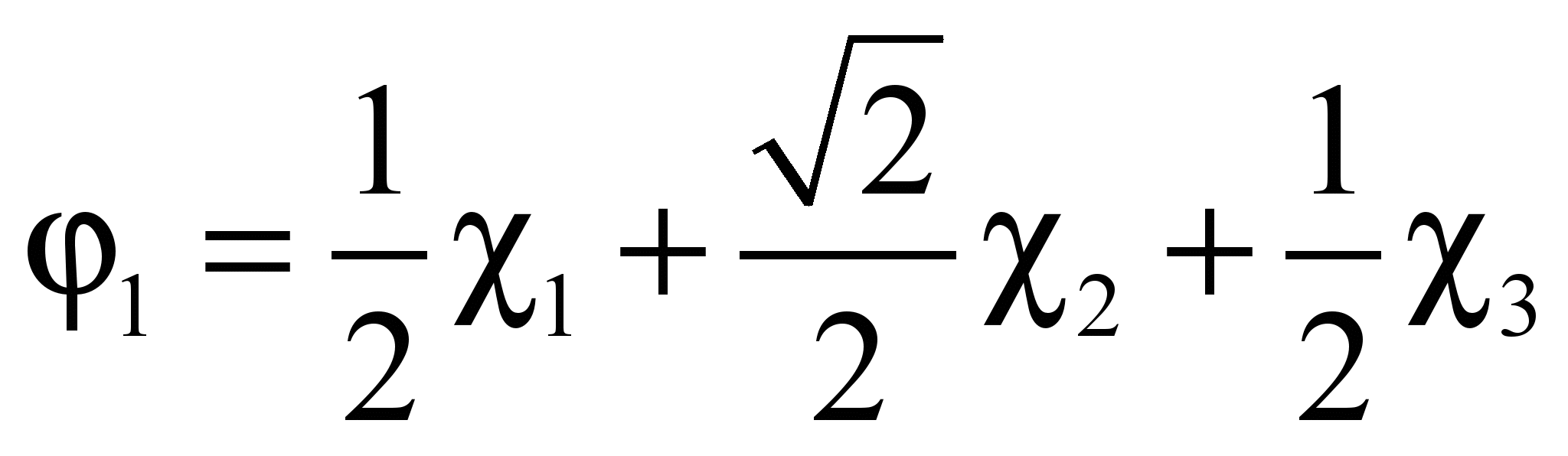
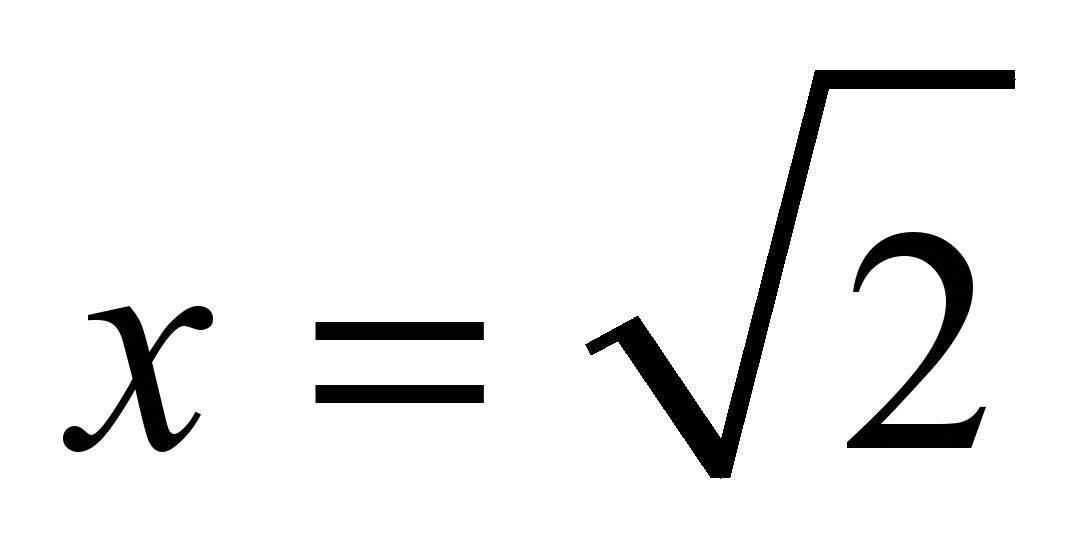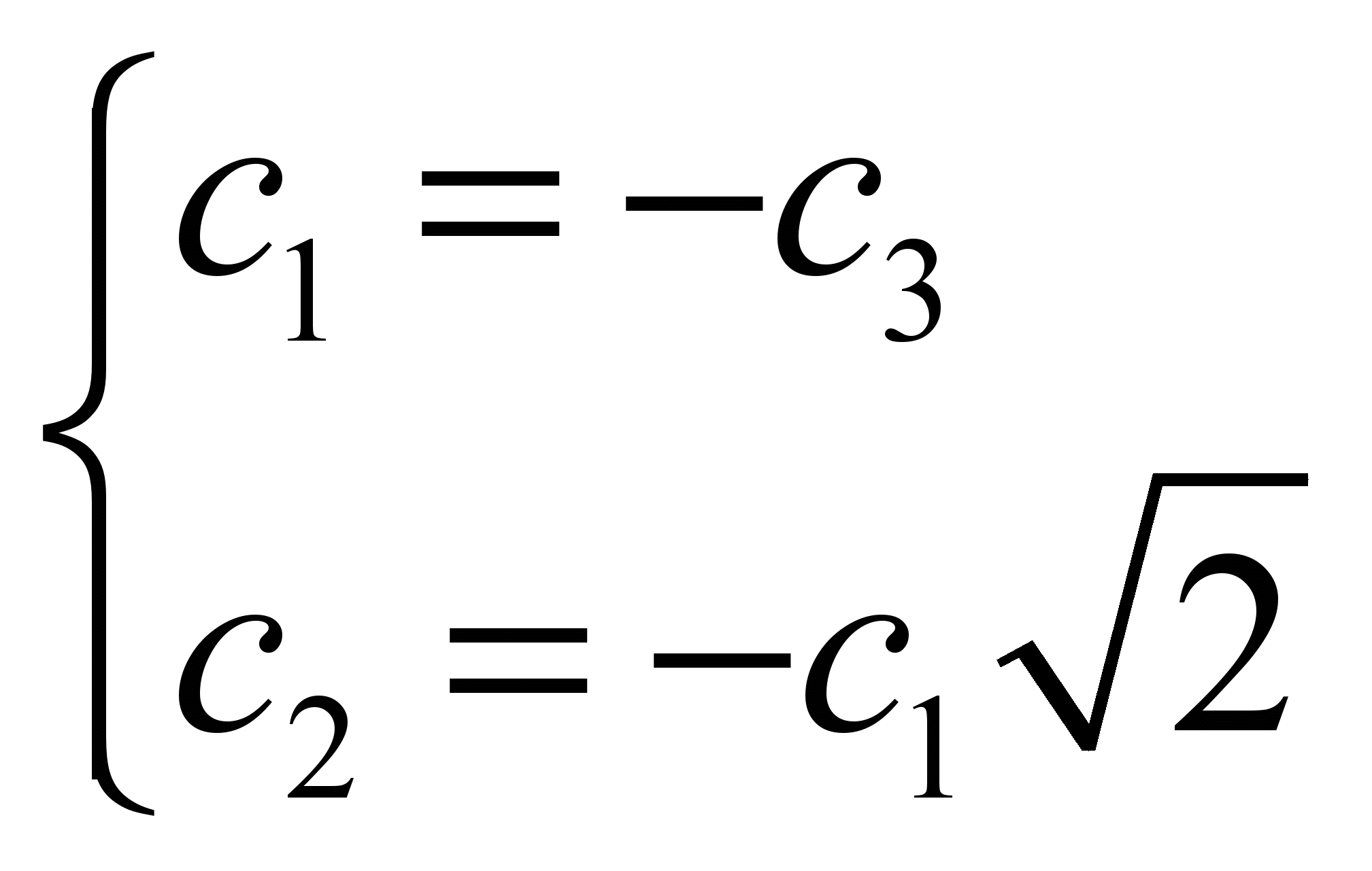
С учетом нормировки



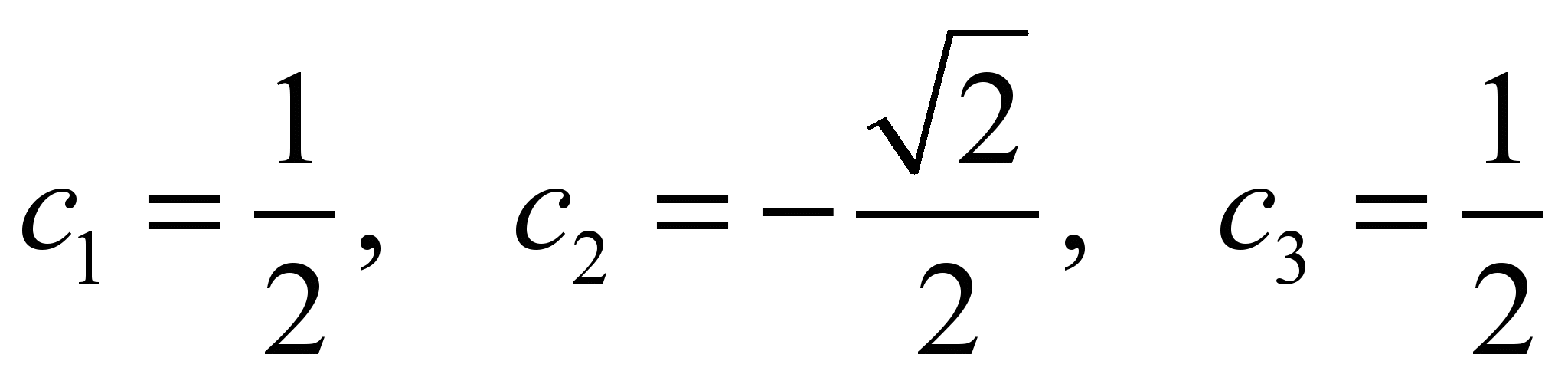
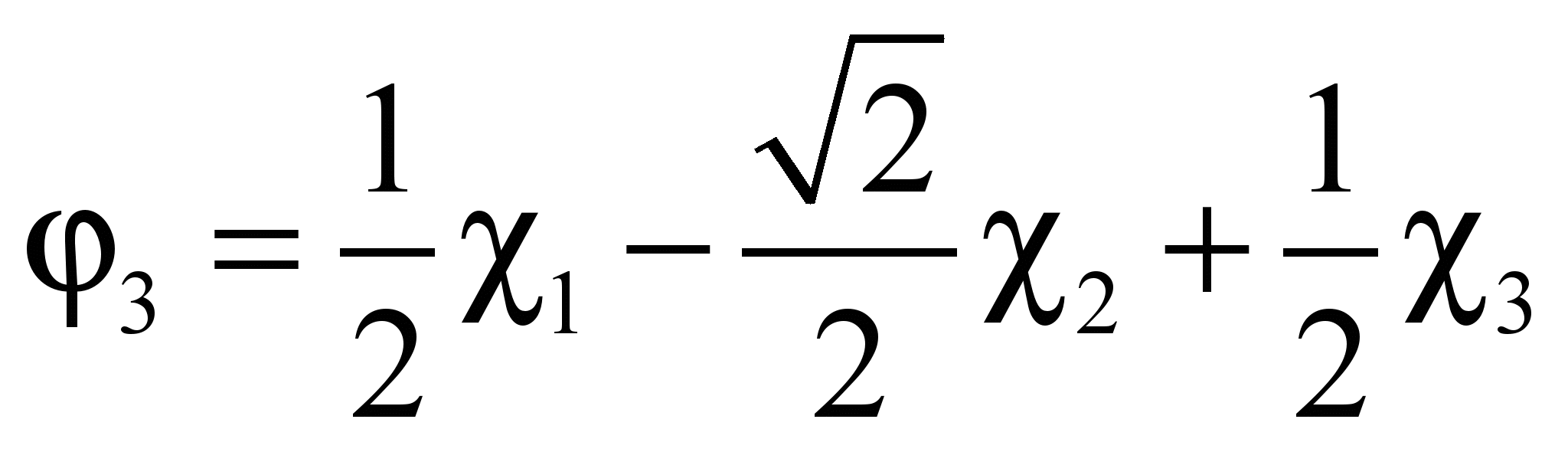
При использовании материалов лекции ссылка на www.students.chemport.ru обязательна.