Программа комплексная психолого-педагогическая практика

Вид материала

Применение статистических критериев.
Схема проверки статистических гипотез (на примере)
Априорная модель ситуации –
Меры связи.
Российский новый университет

Подобный материал:

1 2 3

Применение статистических критериев.

Для проверки статистических гипотез используются различные статистические критерии. Выбор наилучшего критерия – задача сложная, но несмотря на их большое разнообразие, существует единая схема построения критериев и проверки статистических гипотез.

Схема проверки статистических гипотез (на примере):

Испытуемый оценивает громкость n раз предъявляемых стимулов двух различных интенсивностей, а экспериментатору необходимо выяснить, зависит ли рассеяние ошибки субъективного оценивания от интенсивности предъявляемого стимула. При этом субъективные оценки громкостей I_x и I _y в опыте оказались равными: х₁,x₂,х_n; у₁, у₂, у_n.

Формализуют ситуацию. Строят ее априорную модель. Априорная модель ситуации – совокупность предложений о «механизме» и виде распределения изучаемой случайно величины.

В нашем примере априорно предполагаем, что х и у распределены нормально с параметрами (I_х,S_х) и (I_у,S_у)

Н₀: S_х = S_у;

Н₁ : S_х ≠ S_у.

Задаются величиной значимости (0,05; 0,01; 0,001). Например: α = 0,05.
Выбирают некоторую функцию от результатов наблюдений.

Если Н₀ верно, то у имеет распределение Фишера с (n – 1, n-1) степенью свободы.

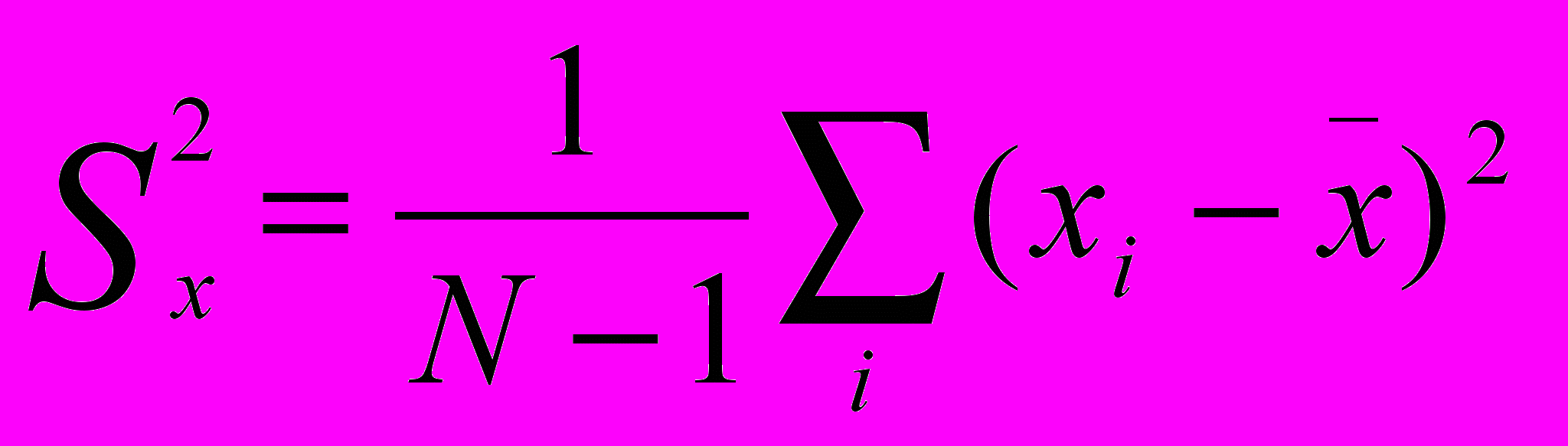
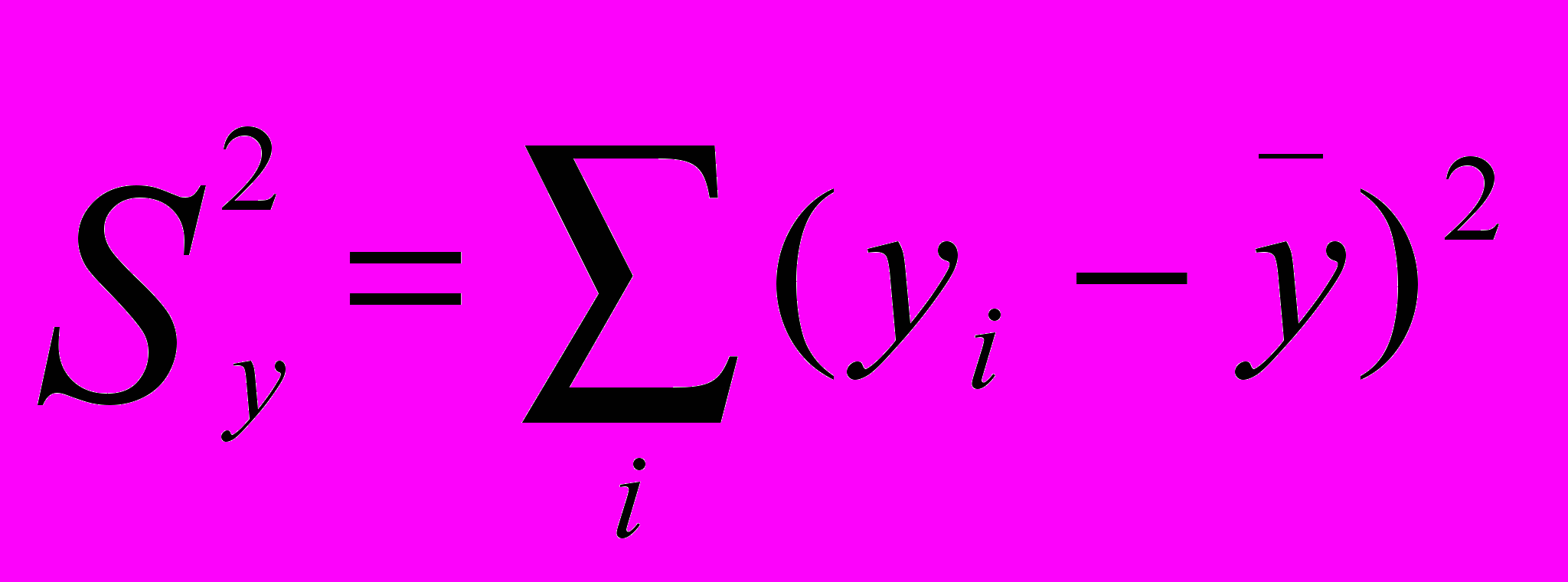
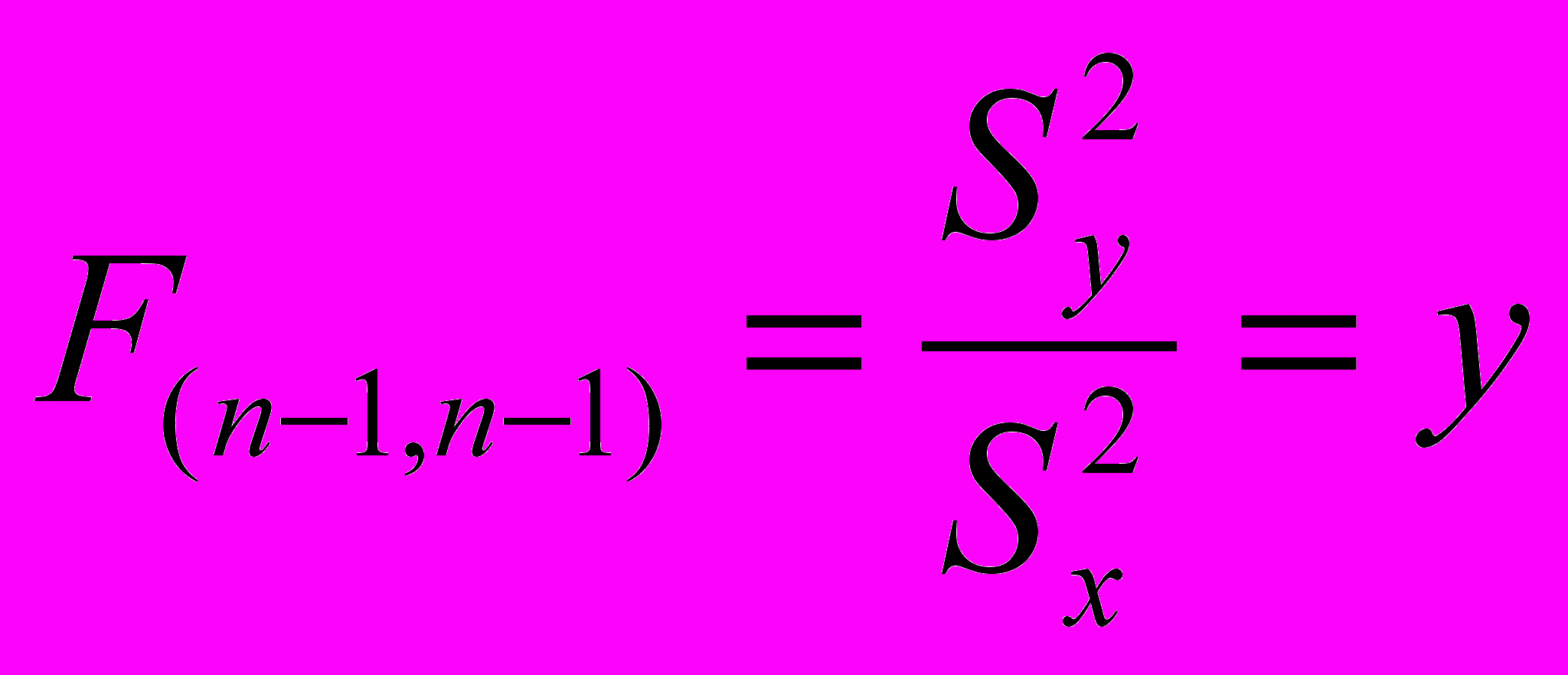
4.Из таблиц распределения находят γ группа максимальная и γ группа минимальная (для двусторонних критериев), распределяющие всю область возможных значений на диапазоны:

- «неправдоподобно малых значений» - вероятность попадания в эту область равна α/2;

- «неправдоподобно больших значений» - вероятность попадания α/2;

- «естественных значений» с вероятностью 1- α.

Пусть n = 21. Тогда γ гр. max =1/2,46, γ гр. min = 2,46.

5.В функцию у подставляют конкретные выборочные значения и находят число γ.

Если γ попадает в область неправдоподобно малых или неправдоподобных больших значений, то гипотезу Н₀отвергают.

Если γ попадает в область правдоподобных значений, то заключают, что данные наблюдений не противоречат высказанной гипотезе (т.е. Н₀– не самая правильная гипотеза, а это одно из возможных естественных утверждений, не противоречащих эмпирическим данным в рамках выбранной априорной модели.

Пусть х: 24,25,32,33,35,35,35,35,38,39,40,40,40,40,40,41,42,42,43,45,47.

У: 20,23,24,25,25,25,26,27,28,30,30,30,30,30,30,30,30,32,32,35,40.

S _x²= 37

S _y²= 19 γ = 37/19 = 1,95

То, что входит в область естественных значений так, что у нас нет оснований считать неправдоподобной гипотезу равенства рассеяния при исследованных интенсивностях.

Критерий для сравнения дисперсий Фишера формулируется так: если рассчитанное значение F окажется больше табличного значения, то Н₀отвергается.

Одной из распространенных задач количественной обработки в психологии является задача проверки значимости различий двух средних значений разных выборок или, другими словами, являются ли две рассматриваемые выборки представителями разных генеральных совокупностей. Для этого часто используется критерий Стьюдента ( в случаях нормального распределения).

,

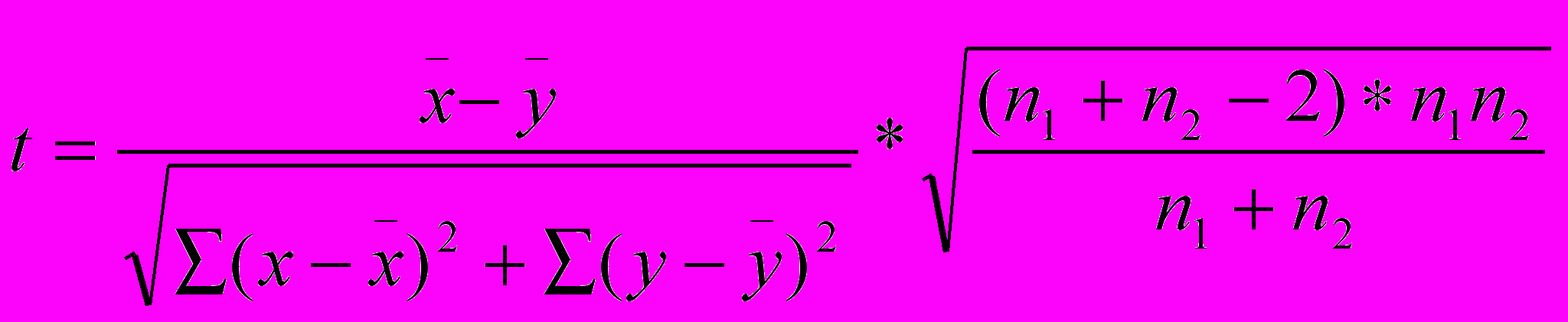где

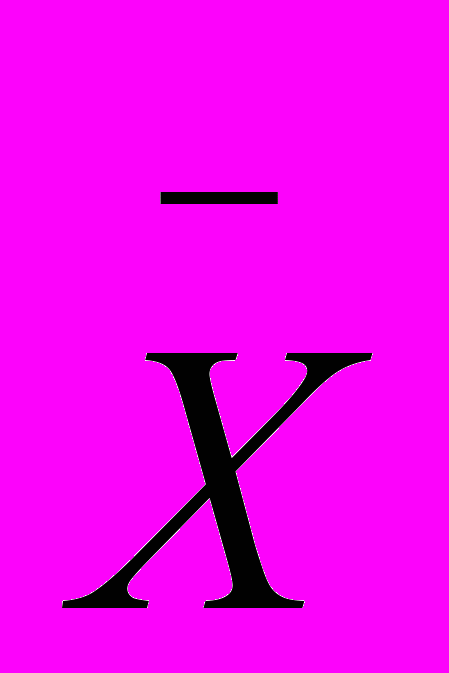
- среднее первой выборки;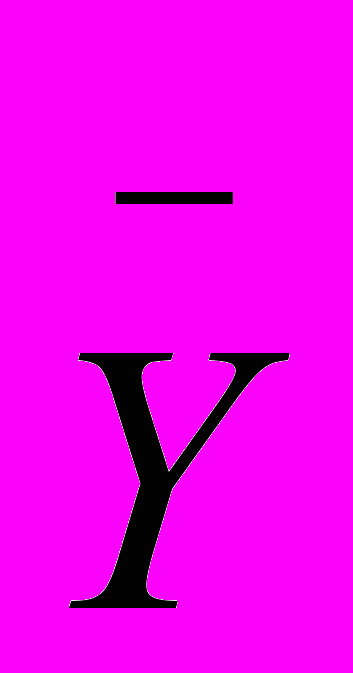

- среднее второй выборки;

n₁– объем первой выборки;

n₂– объем второй выборки.

Пример:

= 526 и n₁= 9,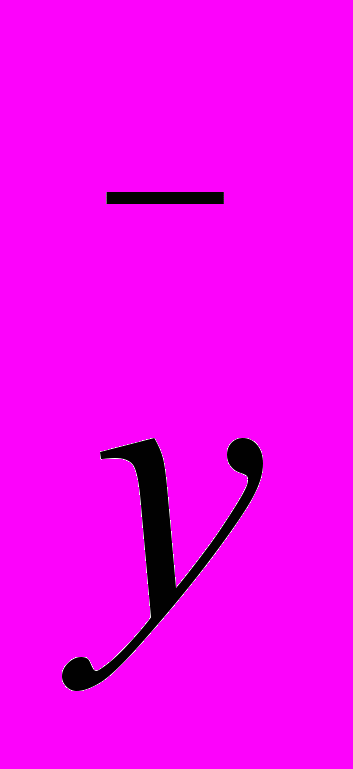

= 638 и n₂= 8.

Находим t = 4,1

Сравним с табличным t = 2,95.

При t (факт.) > t (табл.) – гипотеза H₀ отвергается.

Фрагмент таблицы для α = 0,01 в различных степенях свободы.

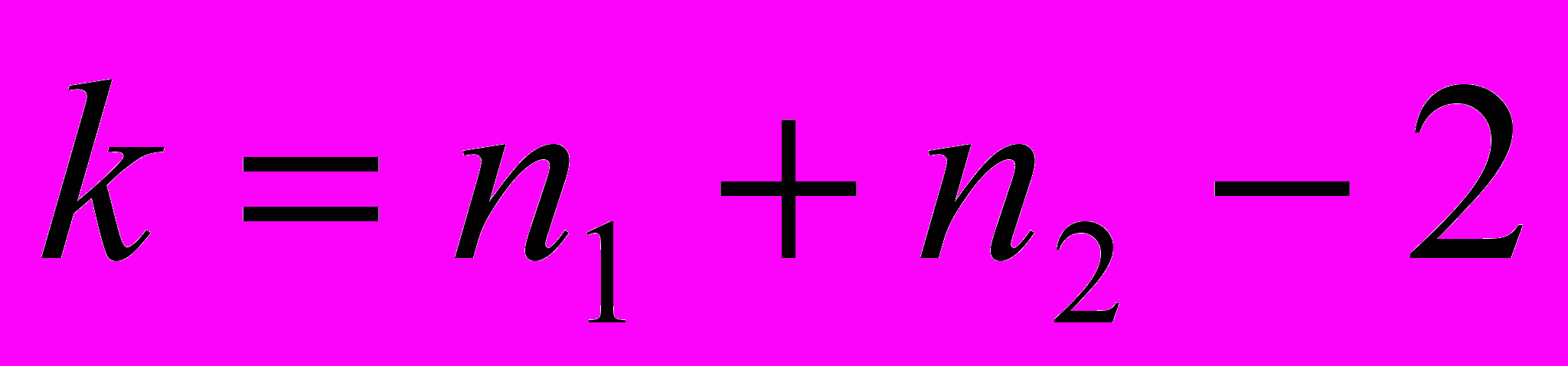
K	5	10	11	12	13	14	15	20	25	30	40	60
T	4.03	3.17	3.11	3.05	3.01	2.98	2.95	2.85	2.79	2.75	2.70	2.66

Для выбранного уровня значимости полученное эмпирическое значение сравнивается с табличным и делается соответствующий вывод о принятии (непринятии) статистической гипотезы (т.е. о статистической значимости различий средних.

Меры связи.

Исследователей часто интересует, как связаны между собой две переменные в данной группе лиц. Для ответа нужно провести наблюдения по каждой переменной для группы объектов (типичных представителей).

Одна из мер связи – линейный (выборочный) коэффициент корреляции или произведение моментов Пирсона:

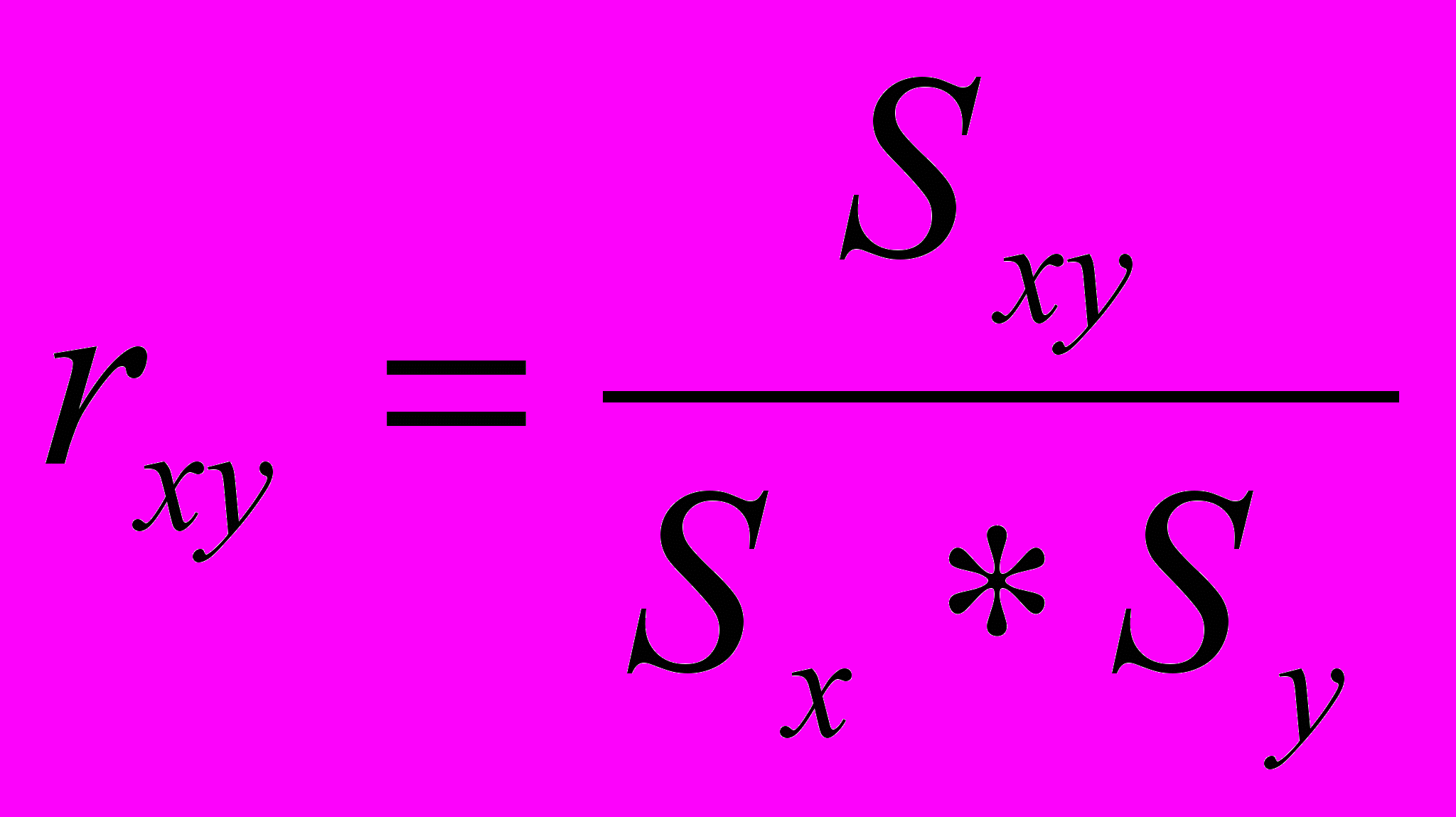, где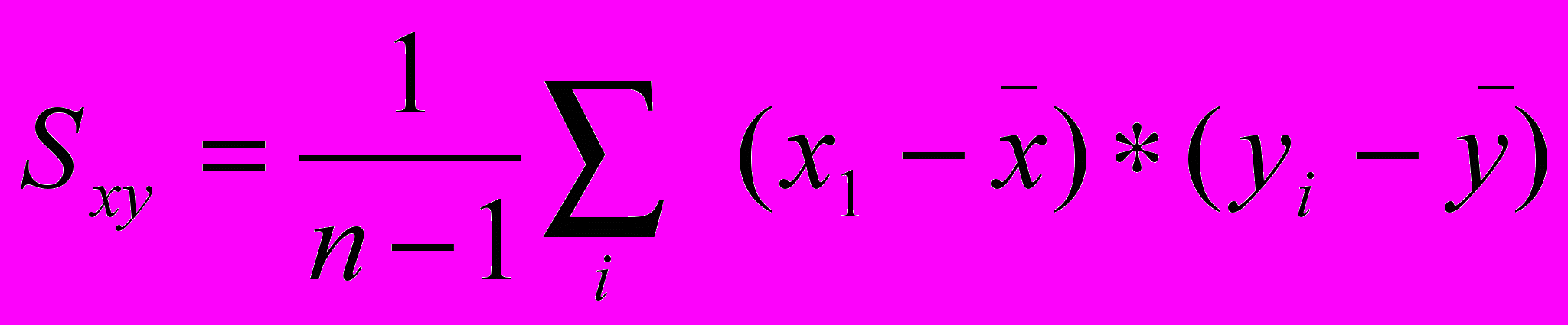

- ковариациях х и у.

S_х– стандартное отклонение данных х;

S_у– стандартное отклонение данных у.

Другой распространенный и простейший коэффициент корреляции – коэффициент ранговой корреляции Спирмена, который измеряет связь между рангами (местами) данной варианты по разным признакам, но не между собственными величинами варианты.

,

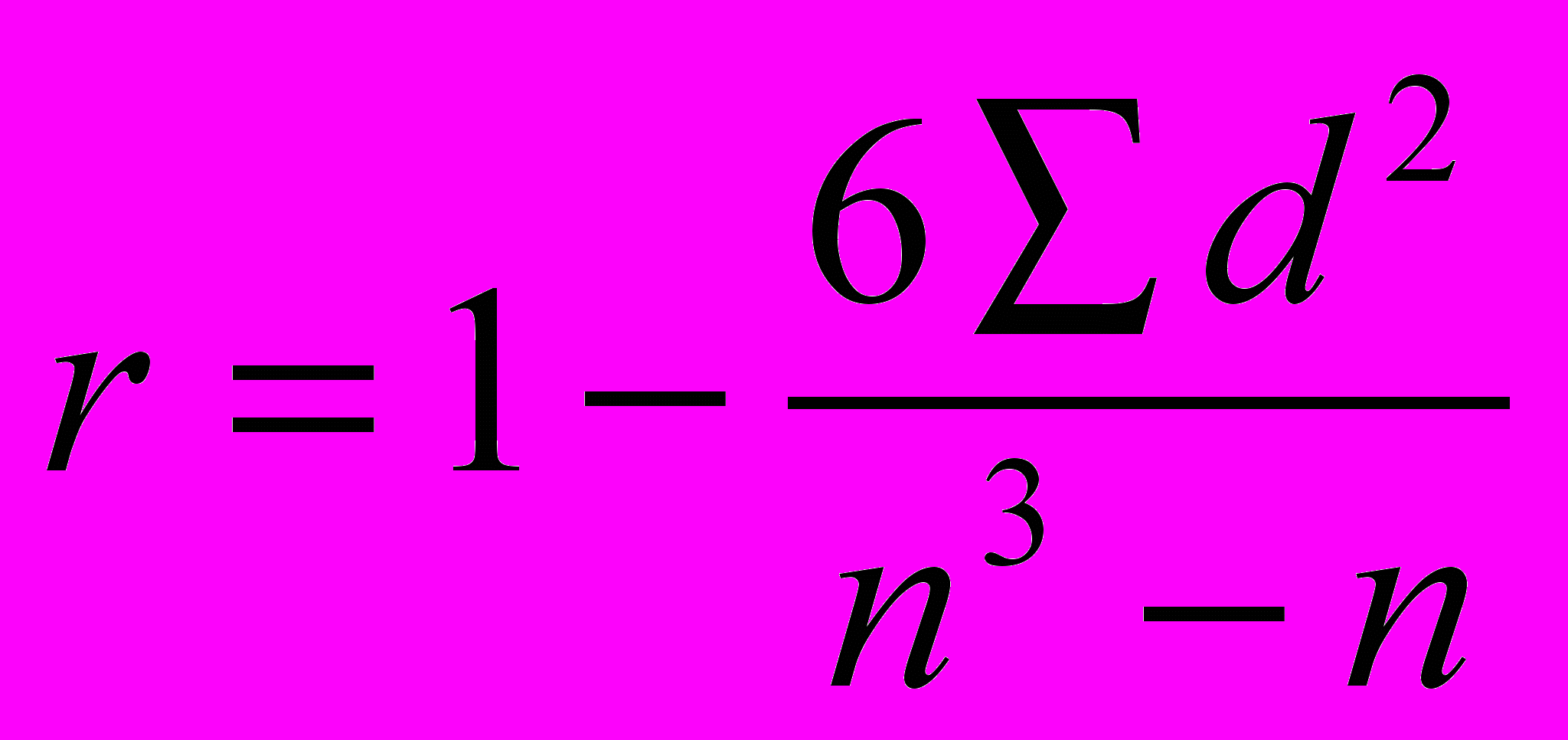где, n – объем совокупности;

d – разность между рангами каждой вариант по двум коррелируемым признакам;

Область изменения коэффициента корреляции:

Коэффициент корреляции изменяется от – 1 до + 1 соответственно с изменением характера связи.

Величина r _xy	Описание линейной связи
+ 1	строгая прямая связь
≈ 0,5	слабая прямая связь
0	нет связи
≈ - 0,5	слабая обратная связь
- 1	обратно пропорциональная

Наиболее современными видами статистического анализа являются: дискриминантный, кластерный, факторный анализы, методы множественной корреляции, регрессия, многомерное шкалирование и др.

Приложение 6

РОССИЙСКИЙ НОВЫЙ УНИВЕРСИТЕТ

(РОСНОУ)

Факультет______________________________________________________

Кафедра________________________________________________________

ОТЧЕТ

о _______________________________________________практике

наименование (учебная, производственная, преддипломная)

Место прохождения практики_________________________________________

Выполнил (а) студент (ка)

______курса______группы

______________________________

фамилия, имя, отчество

Руководство практики от кафедры

______________________________

ученая степень, звание, должность

__________________________

фамилия, имя, отчество

Руководитель практики от организации

__________________________________

должность

__________________________________

фамилия, имя, отчество

Москва 200_

Приложение 7

ПЛАН

написания отчета_________________________________________практики

наименование практики

Общая характеристика организации, где проходила практика, анализ ее деятельности:

- организационно-правовая форма;

- сфера деятельности;

- характер услуг, работ;

- общая характеристика деятельности;

- организационная структура;

- функции организации.

Анализ работы отдела, где проходила практика, или организации.
Функциональные обязанности должностного лица, в должности которого студент проходил практику.
Содержание выполненных практикантом видов работ по программе практики.
Выводы и рекомендации.
Предложения по улучшению организации практики.

Приложение 8

План-задание

преддипломной практики

_________________________________________________________________

(Ф.И.О. студента)

Тема дипломной работы ____________________________________________

_________________________________________________________________

Место прохождения практики_______________________________________

_________________________________________________________________

_________________________________________________________________

(наименование организации, учреждения)

№ п/п	Содержание работы	Сроки	Отметка о выполнении
1	2	3	4

Научный руководитель

дипломной работы ___________________

Руководитель практики ___________________

Студент ___________________

«____________» 200_

Blog

Программа комплексная психолого-педагогическая практика