Петрищева Светлана Николаевна учитель математики моу «сош №4» г. Называевска Омской области Тема урок

Вид материала

Урок

Содержание Ход урока Учитель математики Учитель химии Учитель химии Сколько грамм соли получает организм при внутривенном вливании 100г физиологического раствора? Содержание солей в морской воде достигает 3,5%. Сколько граммов соли останется после выпаривания 10кг морской воды?

Подобный материал:

• Урок русского языка ( 2 класс ) Тема: правописание непроверяемых, 195.36kb.
• Организационно-педагогические условия функционирования педагогической технологии исследования, 304.79kb.
• Классен Светлана Викторовна, учитель математики высшей категории моу «Красногвардейская, 226.21kb.
• Урок геометрии и информатики. Тема урока по учебному плану: Построение правильных многоугольников, 131.04kb.
• Гусева Татьяна Валентиновна, учитель истории моу черногубовская оош калининского района, 120.19kb.
• Алтынник Антонина Николаевна учитель изобразительного искусства моу вейделевская сош, 39kb.
• Змановская Надежда Николаевна, Учитель литературы, моу: сош п. Горноправдинск урок, 121.81kb.
• Рогозина Светлана Яковлевна, учитель информатики моу сош №12 мо г-к Анапа, педагогический, 147.99kb.
• Самойлова Надежда Николаевна, учитель русского языка и литературы моу «Черлакская сош», 293.17kb.
• Чинькова Елена Николаевна Учитель математики первой категории моу томинской сош конспект, 22.98kb.

Петрищева Светлана Николаевна

учитель математики

МОУ «СОШ №4» г.Называевска

Омской области


Тема урока: Решение химических задач с помощью пропорций. (8 класс)


Форма урока: Интегрированный урок (математика+химия)


Цель: развитие умений применения пропорций для решении химических задач

Задачи урока:

- образовательная: обобщить и систематизировать знания обучающихся по теме «Пропорция» и «Массовая доля вещества в растворе»;

- развивающая: развивать вычислительные навыки, умения применять знания на практике;

- воспитательная: воспитывать интерес к предмету и чувство взаимопомощи.


Сопровождение к уроку – компьютерная презентация (Приложение 1)


Ход урока:

1. Организационный момент.
   
2. Историческая справка
   

Пропорции в Древней Греции.

Слово «пропорция» латинского происхождения «proportio», означающее вообще соразмерность, определённое соотношение частей между собой. В древности учение о пропорциях было в большом почёте у пифогорейцев. С пропорциями они связывали мысли о порядке и красоте в природе, о созвучных аккордах в музыке и гармонии во вселенной. Некоторые виды пропорций они поэтому и называли «музыкальными», «гармоничными».

В ІV веке до н.э. общая теория пропорций для любых величин (соизмеримых и несоизмеримых) была создана трудами древнегреческих учёных, среди которых выдающееся место занимали Теэтет и Евдокс. Эта теория подробно изложена в книгах «Начала» Евклида. Пропорциями пользовались для решения разных задач и в древности, и в средние века, и сейчас.

Пропорции применяются не только в математике, но и в архитектуре, искусстве.

Заслуженное место заняла теория пропорций при решении задач по химии.

3. Повторение материала.
   

а) Учитель математики:

1. Что называют пропорцией?
   

2. Прочитайте равенства, записанные на доске:

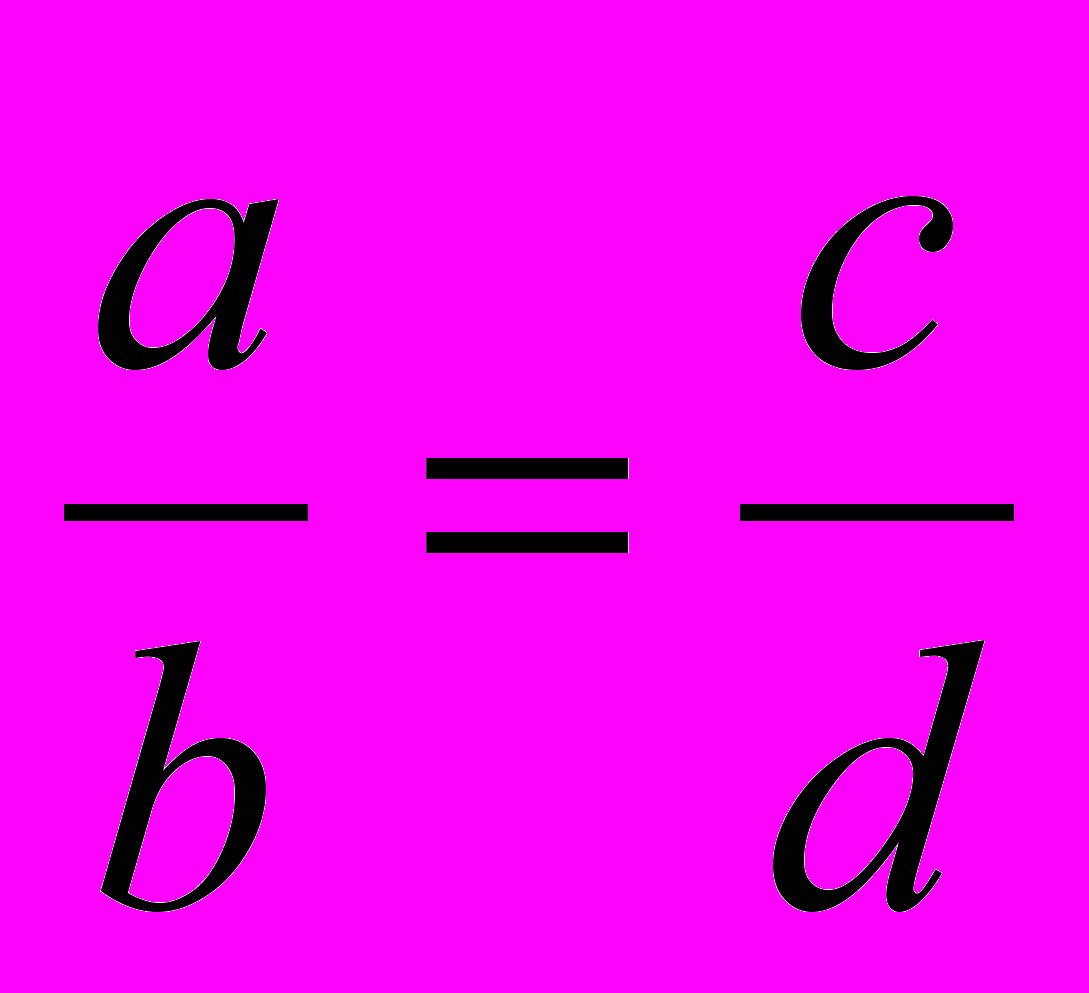; ; 0,2:0,3=40:60;

3. Назовите крайние и средние члены пропорции;

4. Сформулируйте основное свойство пропорции;

5. Найдите неизвестные члены пропорций:

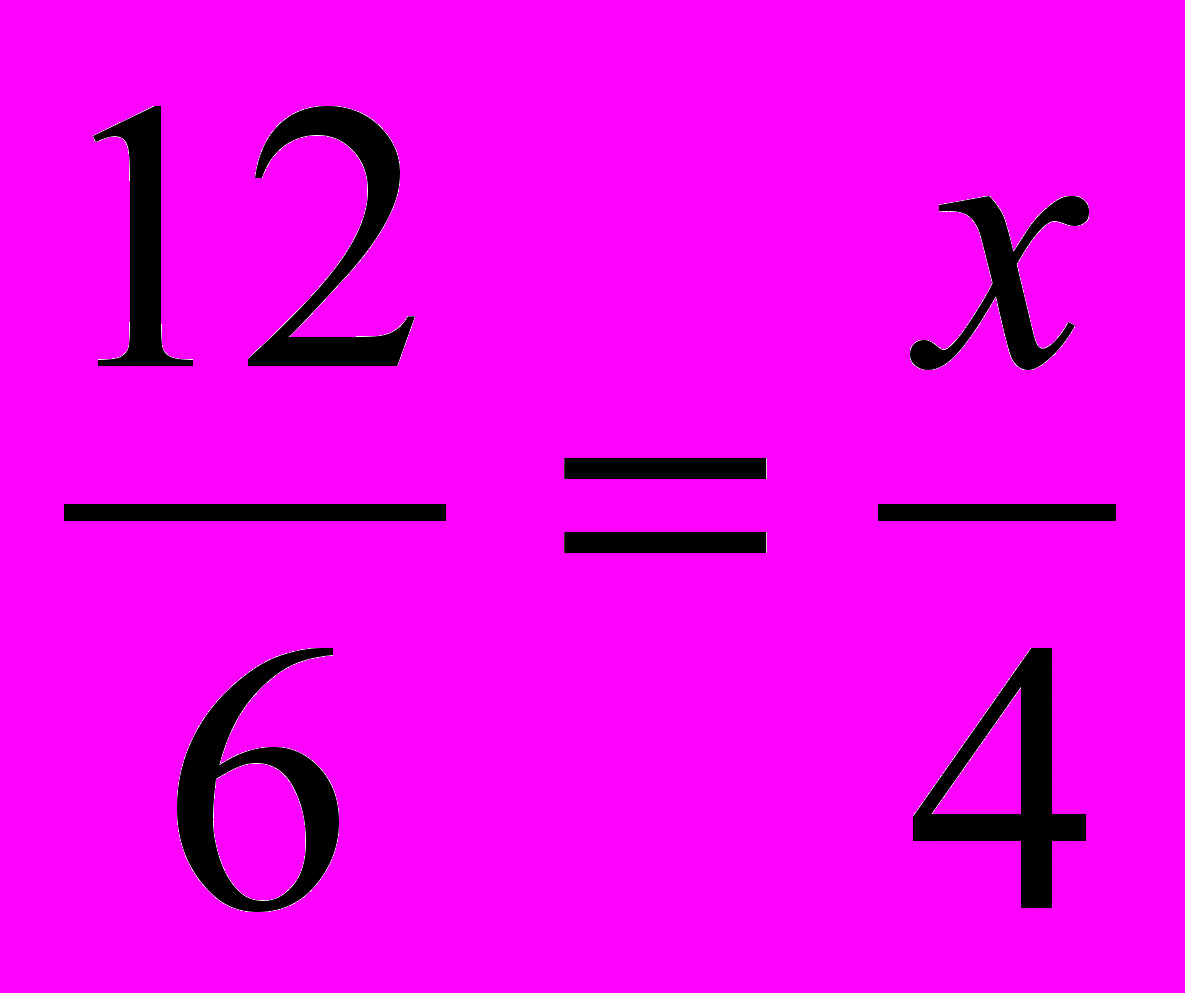; ; 3:y=2:5.

б) Учитель химии:

- Что называют растворами?

- Какие бывают растворы?

- Что такое процентная концентрация?

- Что показывает процентная концентрация?

- Из чего состоит любой раствор?


Запишем обозначение: m_в- масса вещества;

m_H2O- масса воды;

m_p=m_в+m_H2O – масса раствора;

m_p=100%

ω% - процентное содержание вещества в

растворах.

4. Применение знаний для решения задач.
   

Задача 1. Приготовить 100г раствора соли CuSO₄ 1% концентрации.


Учитель химии:

- Что такое концентрация?

- Что необходимо знать для приготовления раствора соли?

- Назовите формулу массы раствора?


Учитель математики:

- Вычислим массу вещества и массу воды с помощью пропорции. Для этого запишем краткое условие задачи:

m_p=100г – 100%

m_в= ? - 1%

m_H2O= ?

- Составим пропорцию: ;

- Выразим неизвестную величину:

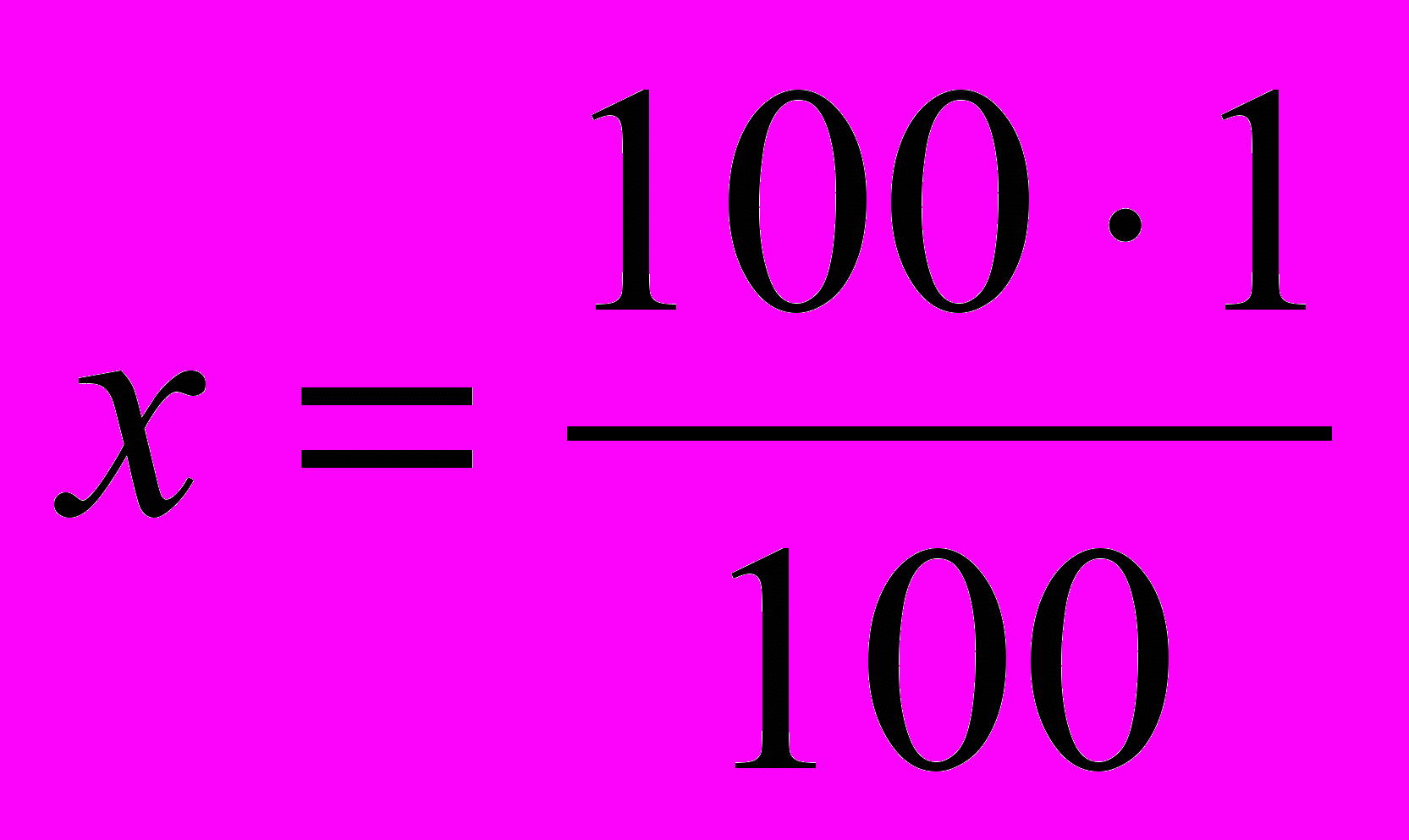
Вывод: получили 1г соли, т.е. m_в=1г.

m_p= m_в+ m_H2O

m_H2O=m_р- m_в

m_H2O=100-1=99 (г)

Ответ: m_в=1г, m_H2O=99г.

По данным задачи учитель химии демонстрирует опыт по получению раствора соли CuSO₄ 1% концентрации. Для этого взвешивает 1г соли CuSO₄ и 99г воды, соединяет, получает раствор массой 100г.


Задача 2. Приготовить 150г раствора с массовой долей хлорида натрия 5%?


Учитель химии:

- Что такое массовая доля?

- Чему она равна по условию задачи?

- Что необходимо знать для приготовления раствора?


Учитель математики:

- Вычислим массу вещества и массу воды аналогично решению первой задачи.


- Известно, что масса раствора составляет 150г, что принимаем за 100%. Составим таблицу по условию задачи.

Условие задачи:	Составление пропорции:	Решение пропорции:	Ответ задачи:
mр=150г – 100% mв= xг – 5%		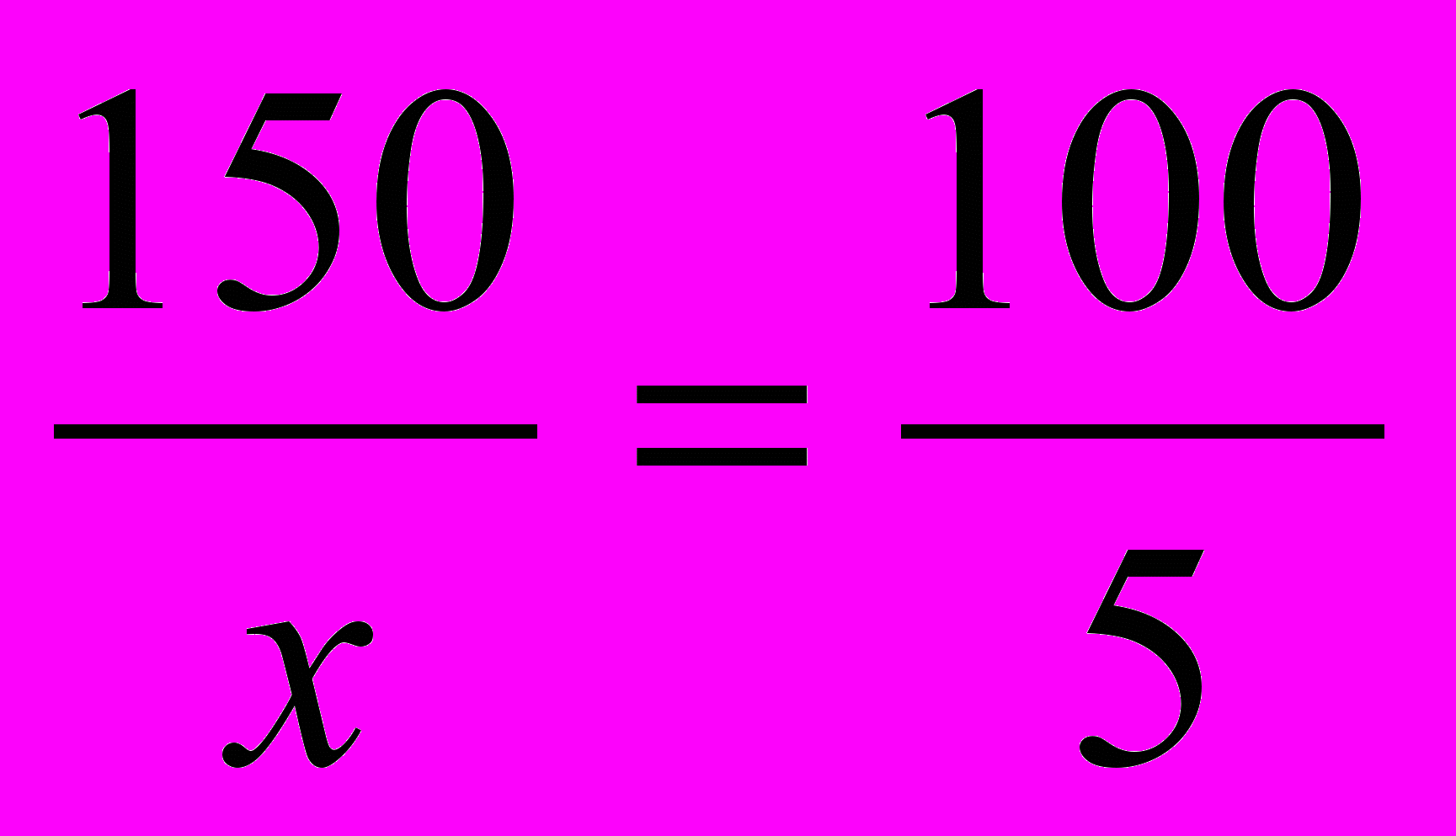(г)	mв=7,5 г mH2O=142,5 г
	mH2O= mр - mв	mH2O=150 – 7,5 =142,5(г)

Учитель химии: демонстрация опыта по получению данного раствора.


Вывод: При решении задач использовались пропорции, связывающие величины m_в, m_р, ω%.



- Выразите из этой пропорции m_в.




Задача 3. Какова процентная концентрация раствора, полученного растворением 5г поваренной соли в 45 г воды?


Ученик у доски оформляет решение задачи.

m_в=5г – х%

m_H2O=45 г

m_p= ? – 100%

1. m_p= m_в+ m_H2O
   

m_p= 5 + 45= 50 (г)

50 г – 100 %

5 г - x %

2) ; %

Ответ: 10% концентрация раствора поваренной соли.


5. Самостоятельная работа (проводится в парах или группах)


Задача 4. Рассчитайте массу вещества и воды для приготовления раствора (120г) с массовой долей соли 8%.


(решения внести в таблицы)

Условие задачи:	Составление пропорции:	Решение пропорции:	Ответ задачи:
mp=100г – 100% mв= ? - 8 % mH2O= ?			mв=9,6г
mp= mв+ mH2O	mH2O=	mH2O=	mH2O=110,4г

Задача 5. Сколько грамм соли получает организм при внутривенном вливании 100г физиологического раствора? ( физиологический раствор – это 0,85% раствор поваренной соли)

Условие задачи:	Составление пропорции:	Решение пропорции:	Ответ задачи:
mp= 100г – 100% mв= ? - 0,85 % mH2O= ?			mв= 0,85г
mp=

Ответ: 0,85г соли.


Задача 6. Содержание солей в морской воде достигает 3,5%. Сколько граммов соли останется после выпаривания 10кг морской воды?

Условие задачи:	Составление пропорции:	Решение пропорции:	Ответ задачи:
mp= mв=

Ответ: 0,35кг соли = 350г в 10кг воды.

6. Контроль решения задач.

Учитель математики:

- Проверим правильность решения задач.


7. Подведение итогов.

Учитель математики:

- Назовите пропорцию, связывающую величины m_p, m_в, ω%.

()

- Выразите из этой формулы величины: m_p, m_в, ω%.


8.Домашнее задание.

Составить таблицу изученных формул.