Учебное пособие для студентов высших учебных заведений, обучающихся по направлению 540200 (050200) «Физико-математическое образование»
| Вид материала | Учебное пособие |
- Учебное пособие для студентов высших медицинских учебных заведений Издание 2-е, дополненное, 955.76kb.
- Учебная программа курса для направления 540200 физико-математическое образование 540202М, 259.65kb.
- Программа вступительных испытаний для лиц, поступающих в магистратуру на направление, 220.49kb.
- Учебное пособие Л. Б. Шнейдер* Г. В. Вольнова, М. Н. Зыкова психологическое консультирование, 2906.59kb.
- Учебное пособие для студентов высших учебных заведений, обучающихся по психологическим, 842.18kb.
- Учебное пособие. 3-е изд., испр и доп, 125.38kb.
- Учебное пособие рекомендовано Министерством общего и профессионального образования, 3469.26kb.
- Учебное пособие для студентов высших учебных заведений Махачкала 2008, 6753.55kb.
- Практикум для вузов Москва владос губарева Л. И., Мизирева О. М., Чурилова Т. М., Практикум, 2037.65kb.
- В. И. Гараджа религиоведение учебное пособие, 5104.37kb.
Приложения
Приложение 1
Требования Государственного стандарта
по теории и методике обучения математике
Государственный образовательный стандарт
высшего профессионального образования (2005 г.)
Общее количество часов — 332.
Математика как наука и учебный предмет в школе. Методическая система обучения математике в школе, общая характеристика ее основных компонентов. Цели и задачи обучения математике в школе.
Методика базового образования основной школы. Общая начальная математическая подготовка в 1—5 классах. Пропедевтическая математическая подготовка в 5—6 классах. Основной систематический курс математики в 7—9 классах (основная школа). Основные блоки: алгебра и геометрия (планиметрия).
Методика изучения курса математики в старших классах средней школы (10—11 классы). Блоки: алгебра, начала анализа и геометрия (стереометрия). Дифференцированное изучение курса математики. Методика обучения математики на профильном уровне. Предпрофильная подготовка. Индивидуальные особенности
и способности школьников в контексте изучения курса математики.
Аудиовизуальные технологии обучения математике. Интерактивные технологии обучения. Дидактические принципы построения аудио-, видео- и компьютерных учебных пособий и методика их применения.
Банк аудио-, видео- и компьютерных учебных материалов.
Использование современных информационных и коммуникационных технологий в учебном процессе. Основные понятия и определения предметной области — информатизация образования. Цели и задачи использования информационных
и коммуникационных технологий в образовании. Информационные и коммуникационные технологии в реализации информационных и информационно-деятель-ностных моделей в обучении. Информационные и коммуникационные технологии в активизации познавательной деятельности учащихся. Информационные и коммуникационные технологии в реализации системы контроля, оценки и мониторинга учебных достижений учащихся.
Методы анализа и экспертизы для электронных программно-методических
и технологических средств учебного назначения. Методические аспекты использования информационных и коммуникационных технологий в учебном процессе.
Приложение 2
Примерная схема анализа внеклассного мероприятия по математике
1. Школа, класс, форма проведения внеклассного мероприятия.
2. Тема внеклассного мероприятия и его цель проведения.
3. Связь темы внеклассного мероприятия с программой по математике данного класса и последующих классов.
4. Целесообразность выбора темы.
5. Участие школьников в подготовительной работе.
6. Научность содержания рассматриваемого математического материала. Углублению каких знаний по математике способствует программа проведенного мероприятия?
7. Доступность материала. Использование наглядности и технических средств обучения.
8. Участие школьников в проведении мероприятия, их активность.
9. Методы обратной связи, использованные учителем.
10. Педагогическая ценность проведенного внеклассного мероприятия.
Приложение 3
Лист наблюдения урока
Школа_______________ Дата_______________ Класс_________
Количество учащихся _____ На уроке______________ Предмет_____________
ФИО учителя ______________________________
Тема:_____________________________________________________
| Наблюдение за деятельностью учителя | Оценка | Наблюдение за работой учащихся | Оценка | ||||
| 1. Организационное начало урока | | | | 1. Внимание учащихся на различных этапах урока: — в начале, — в середине, — в конце | | | |
| 2. Повторение и проверка знаний | | | | ||||
| 3. Теоретический уровень изложения: а) научность; б) логичность; в) систематичность; г) последовательность; д) доступность | | | | 2. Активность учащихся: — при опросе, — при изучении, — при закреплении | | | |
| 4. Отбор учебного материала | | | | 3. Прочность знаний, умений и навыков | | | |
| 5. Целостность раскрытой темы | | | | 4. Самостоятельность суждений | | | |
| 6. Организация, внимания учащихся | | | | 5. Интерес к теме | | | |
| 7. Воспитательная сторона урока | | | | 6. Речь учащихся | | | |
| 8. Использование ТСО, элементов наглядности, дидактического материала | | | | 7. Культура труда | | | |
| 9. Речь учителя: а) грамотность; б) эмоциональность; в) четкость | | | | 8. Взаимоотношения учащихся с учителем | | | |
| 10. Педагогический такт | | | | 9. Самоконтроль и взаимоконтроль | | | |
| 11. Индивидуальный и дифференцированный подход | | | | 10. Дисциплина:
| | | |
| 12.Организация самостоятельной работы: а) цель; б) содержание; в) методика | | | | ||||
| 13. Расчет времени | | | | ||||
| 14. Домашнее задание | | | | ||||
Примечание: Действия учителя и учащихся оцениваются по пятибалльной шкале.
Приложение 4
Примерная схема анализа урока
Общие сведения об уроке: школа, класс, предмет, ФИО учителя, тема урока, цель и тип.
1) Оценка реализации задач урока:
— четкость постановки задач учителем;
— эффективность их решения.
2) Оценка организации урока:
— готовность учителя и учащихся к уроку;
— мобилизующее начало урока;
— рациональное распределение времени этапов урока;
— соответствие структуры урока его типу;
— нормирование и дифференциация домашнего задания;
— подведение итогов урока.
3) Оценка реализации дидактических принципов с точки зрения оптимальности их сочетания:
— научность и доступность;
— наглядность и абстрактность;
— систематичность и последовательность.
4) Оценка содержания урока:
— объем фактического материала, соответствие программе;
— связь теории с практическими заданиями;
— связь текущего и ранее изученного материала;
— повторение пройденного;
— внутрипредметные и межпредметные связи, связь с жизнью.
5) Оценка методов, форм и средств обучения:
— целесообразность их выбора;
— наличие обратной связи «учитель — ученик»;
— методы проверки и оценки знаний учащихся;
— дифференцированный подход;
— сочетание коллективной, групповой, индивидуальной работы учащихся;
— средства достижения и поддержки внимания учащихся и развития интереса к предмету.
6) Психологический микроклимат на уроке:
— взаимоотношения учителя и учащихся;
— справедливость требований и объективность оценок;
— меры поощрения деятельности учащихся.
7) Оценка здоровьесберегающих условий урока:
— соблюдение санитарно-гигиенических норм.
8) Оценка результативности урока:
— эффективность урока;
— ценные стороны и недостатки;
— предложения учителю.
Приложение 5
Требования, предъявляемые при публичной защите
конспектов уроков по ТиМОМ
Для проведения публичной защиты подготовить презентации в программе PowerPoint.
Презентация должна содержать слайды, отображающие:
— тему урока, цели урока (образовательные, воспитательные, развивающие), тип урока;
— примерный план урока с указанием времени, выделенного на каждый этап урока;
— систему упражнений, соответствующую каждому этапу урока, ряд заданий можно привести с решением, которые будут иллюстрировать необходимость их включения в данную систему упражнений. В ходе выступления (защиты) необходимо провести методический анализ каждого этапа урока, включающий:
— цель данного урока;
— обоснование подбора упражнений для этого этапа;
— указание используемых приемов сознательного усвоения материала урока, повышения интереса к уроку, развития учащихся;
— оборудование, используемое на рассматриваемом этапе урока.
Время защиты 5—10 мин. Содержание презентации следует записать на электронный носитель и заранее проверить, будет ли файл открываться на компьютере, используемом на занятии. По техническим вопросам обращаться к лаборанту кафедры.
В течение недели можно получить консультацию по методике подготовки урока (презентаций) у преподавателя, ведущего занятия по предмету.
Приложение 6
Конспект урока
Тема: «Сфера и шар. Уравнение сферы».
Класс: 11.
Тип урока: урок формирования знаний.
Цель урока: сформировать понятия сферы, шара и их элементов (центра, радиуса, диаметра); рассмотреть определение уравнения поверхности и вывести уравнение сферы в заданной прямоугольной системе координат.
Оборудование: доска, учебник, модели сферы и шара, полуокружности и полукруга.
Литература:
- Геометрия: учеб. для 10—11 кл. общеобразоват. учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев [и др.]. — 5-е изд. — М. : Просвещение, 1991. — 256 с.
- Геометрия. 11 класс: поурочные планы по учебнику Л. С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева [и др.] / авт.-сост. Г. И. Ковалева. — Волгоград: Учитель, 2006. — 169 с.
- Саакян С. М., Бутузов В. Ф. Изучение геометрии в 10—11 классах: методич. рекомендации к учебнику : кн. для учителя. — М. : Просвещение, 2001. — 222 с.
План урока
- Организационный момент.
- Актуализация знаний.
- Введение новых знаний.
- Подведение итогов изучения темы урока.
- Постановка домашнего задания и инструктаж по его выполнению.
Ход урока
| № | Действия учителя | Действия ученика | Методы обучения | Средст-ва обу-чения | Форма обуче-ния |
| 1 | Учитель заходит в класс, приветствует учеников. Объявляет тему урока и записывает ее на доске: «Сфера и шар. Уравнение сферы» | Ученики приветствуют учителя. Записывают в тетрадях тему урока | | | |
| 2 | Учитель задает ученикам вопросы: Дайте определение окружности, ее центра. Дайте определение круга. Фигуры, которые мы с вами рассмотрели, располагались на плоскости. В пространстве аналогами этих фигур будут выступать сфера и шар. В жизни вы неоднократно сталкивались с этими телами: глобус, мяч, земной шар. Давайте дадим определение сферы, аналогичное определению окружности: Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Данная точка называется центром сферы. | Ученики отвечают на вопросы учителя: Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Эта точка называется центром окружности. Часть плоскости, ограниченная окружностью, называется кругом. | Опрос | Модель сферы | Фрон-тальная |
Продолжение
| | Что называют радиусом окружности? Сформулируйте аналогичное определение для радиуса сферы. Как обозначались центр и радиус окружности? Центр и радиус сферы обычно обозначают теми же буквами. Кто попробует дать определение диаметра сферы? Как он выражается через радиус сферы? Так же, как цилиндр и конус, сфера является телом вращения. Она может быть получена вращением полуокружности вокруг ее диаметра (учитель демонстрирует это на модели полуокружности). Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара (показывает шар и его элементы на модели). Он может быть получен вращением полукруга вокруг своего диаметра (демонстрирует на модели полукруга). Шар радиуса R с центром О содержит все точки пространства, которые расположены от точки О на расстоянии, не превышающем R, и не содержит других точек. | Отрезок, соединяющий какую-нибудь точку окружности с ее центром, называется радиусом окружности. Отрезок, соединяющий какую-нибудь точку сферы с ее центром, называется радиусом сферы. Центр обозначался буквой О, а радиус — R. С помощью учителя один из учеников дает определение диаметра сферы: Отрезок, соединяющий две точки сферы и про-ходящий через ее центр, называется диаметром сферы. Он равен 2R. | Беседа Демонст-рация | Модель полуок-ружнос-ти Модель шара. Модель полукруга | |
Продолжение
| | После объяснения учитель рисует на доске сферу и отмечает её элементы. Что называют уравнением линии на плоскости? Рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Сформулируем определение уравнения поверхности: уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности. Вызывает одного из учеников к доске, чтобы записать уравнение окружности. Выведем уравнение сферы радиуса R с центром в точке C(x0, y0, z0). Запишите формулу, по которой вычисляется расстояние между произвольной точкой М(x, y, z) и центром сферы С. Из определения сферы нам известно, что оно будет одним и тем же для всех точек сферы и равным R. Значит, 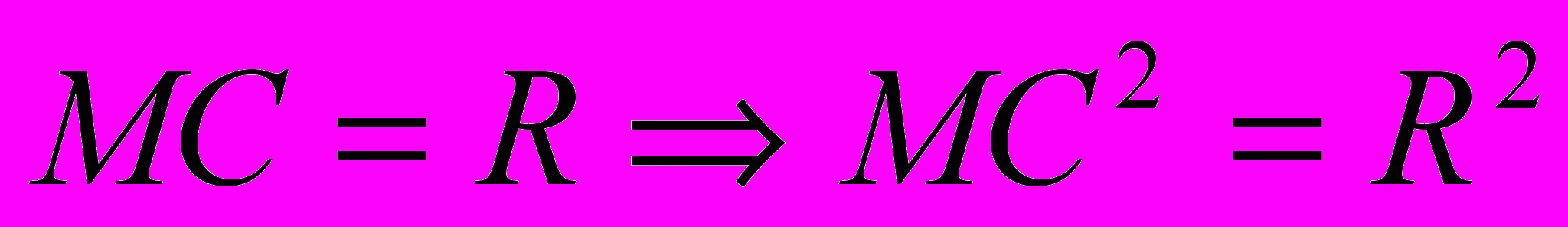 , то есть координаты точки М удовлетворяют уравнению , то есть координаты точки М удовлетворяют уравнению 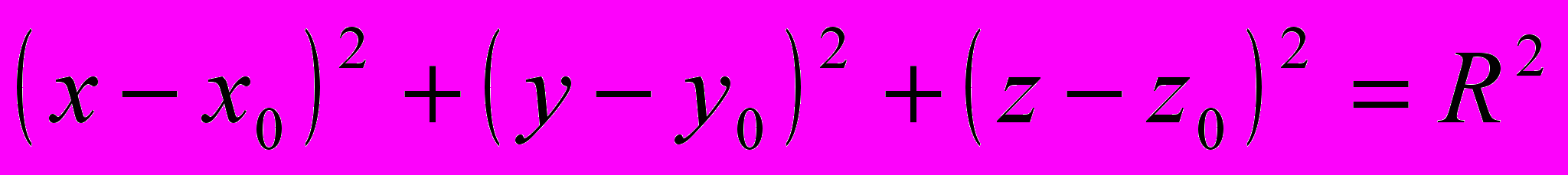 (1). (1). | Ученики рисуют сферу и ее элементы у себя в тетрадях. Уравнение с двумя переменными x и y называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии. 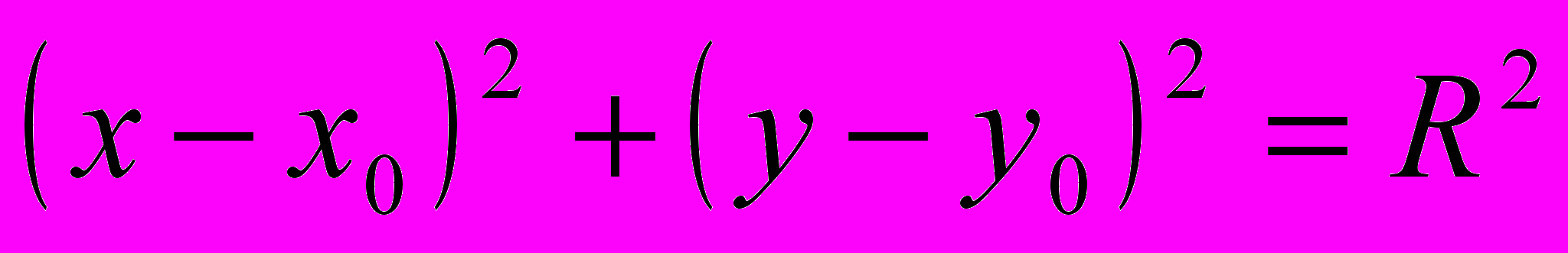 , где точка , где точка 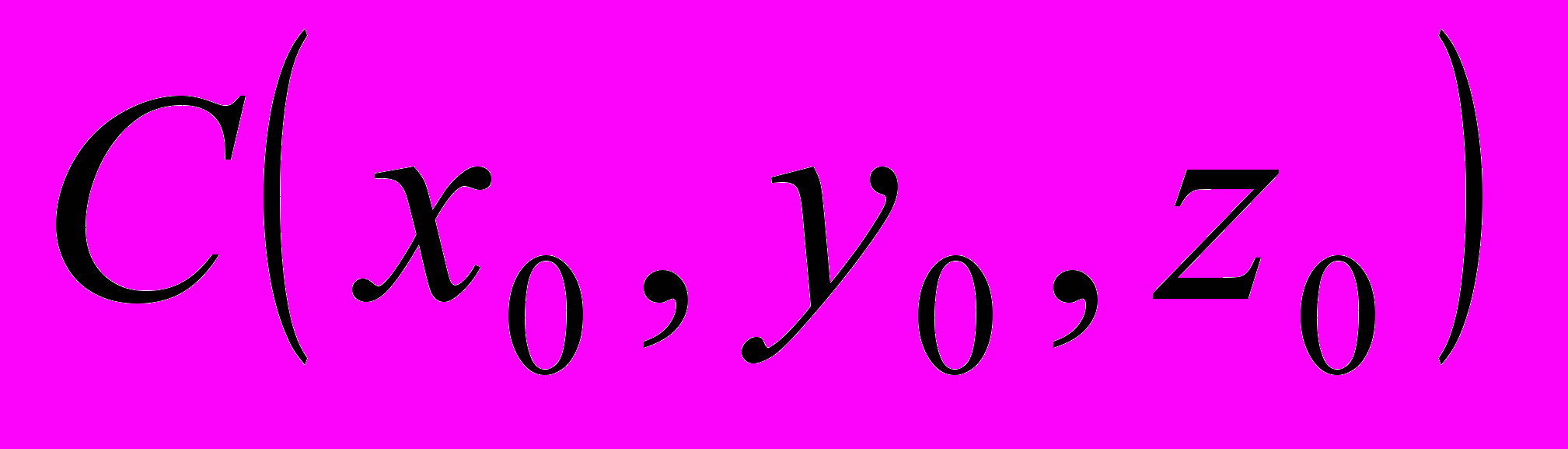 — центр окружности, а R — ее радиус. — центр окружности, а R — ее радиус.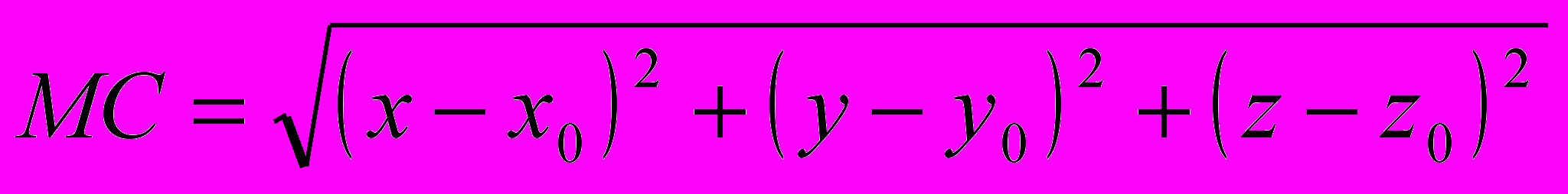 Записывают вывод уравнения в тетрадях. | Объясне- ние | | |
Продолжение
| | Если же точка М(x, y, z) не лежит на данной сфере, то 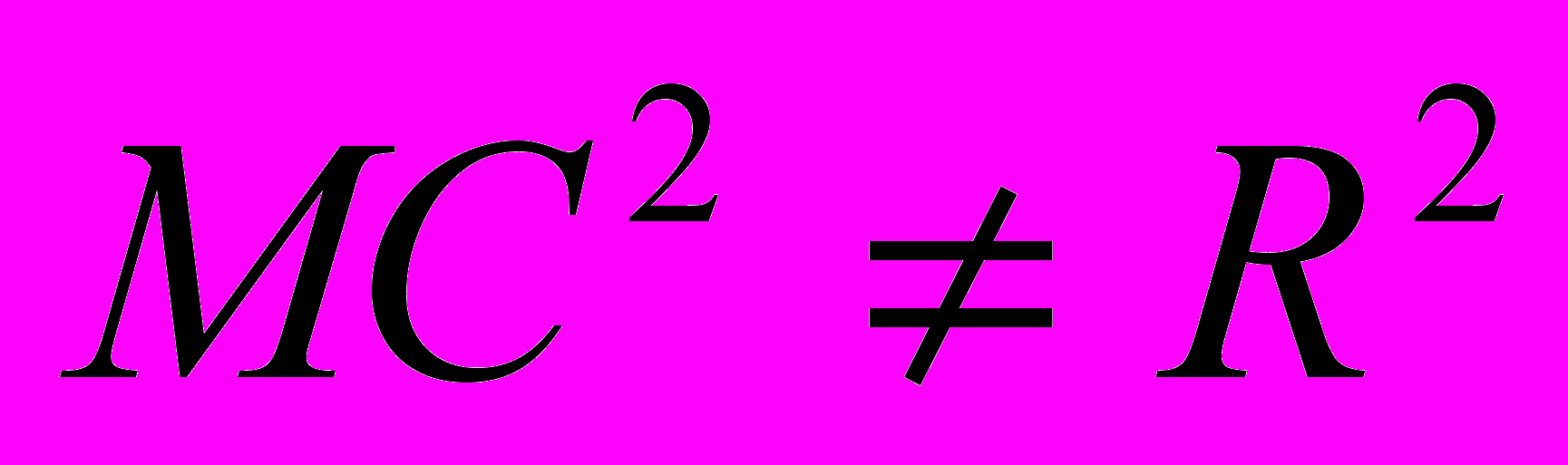 , то есть координаты точки М не удовлетворяют уравнению (1). , то есть координаты точки М не удовлетворяют уравнению (1).Следовательно, в прямоугольной системе координат уравнение сферы радиуса R с центром С(x0, y0, z0) имеет вид 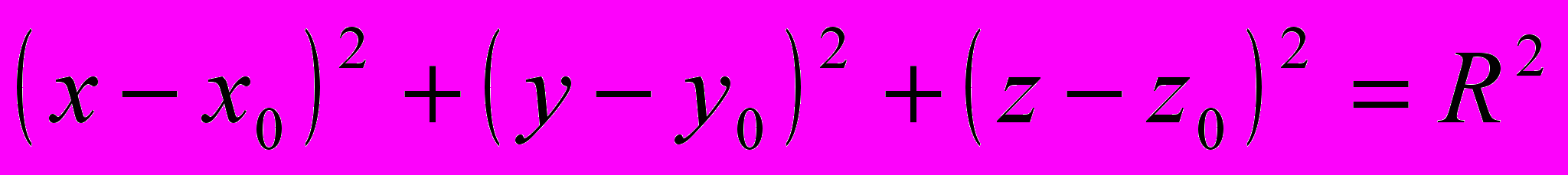 . .Учитель предлагает определить, являются ли данные уравнения уравнениями сферы: a) 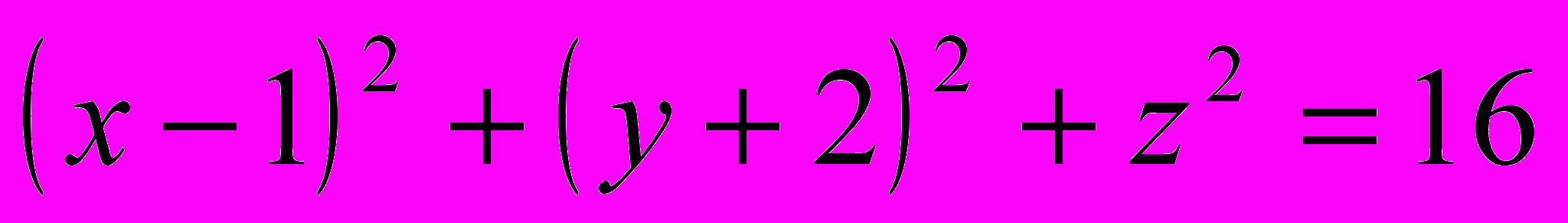 , ,б) 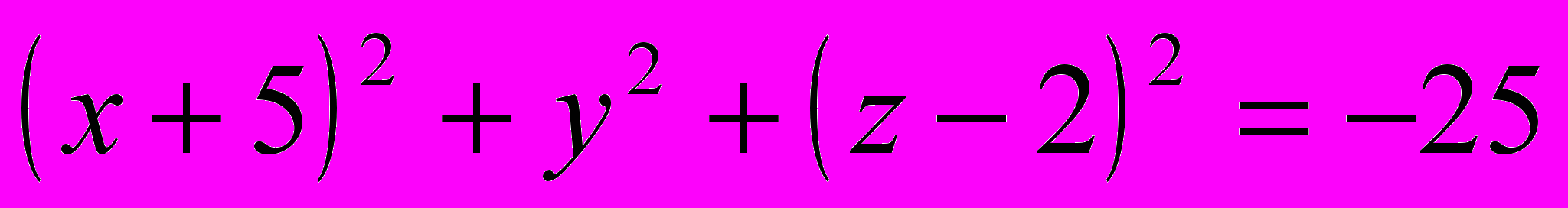 , ,в) 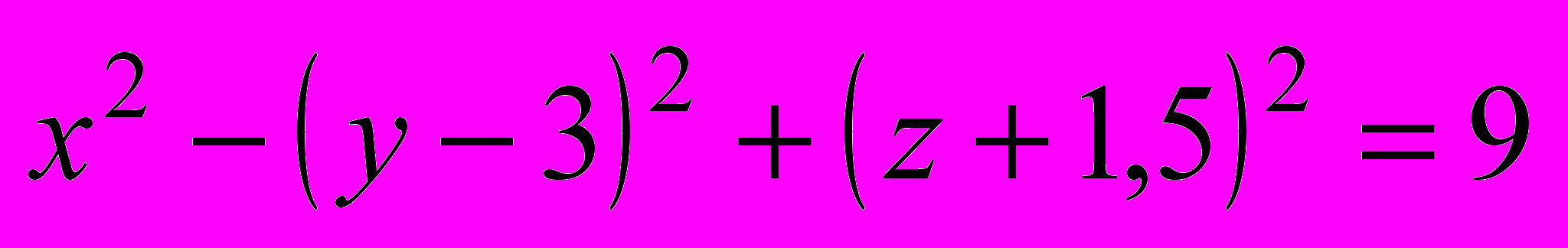 , ,г) 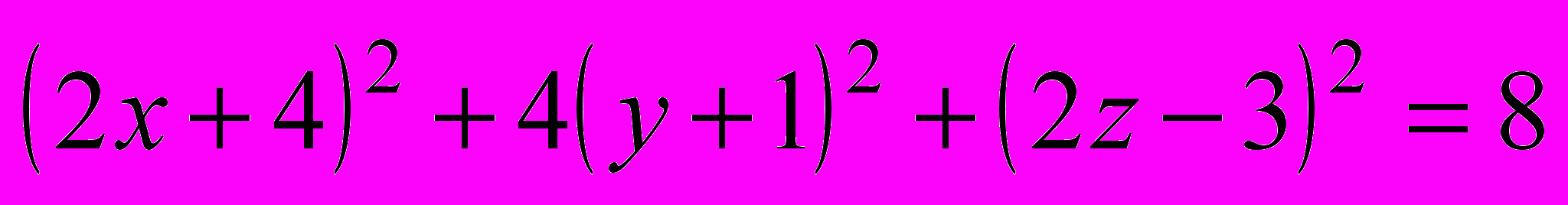 . . | а) Да. 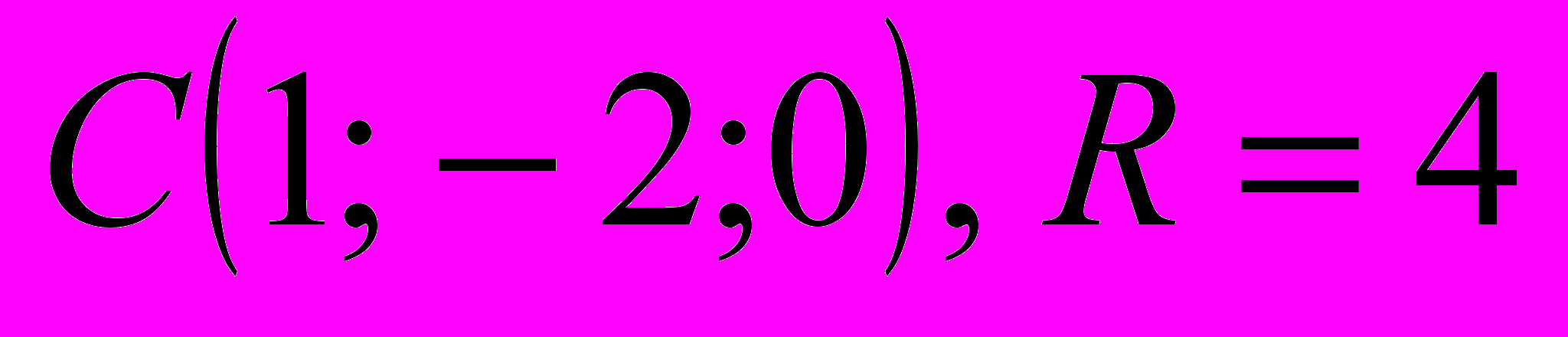 . .б) Нет, так как квадрат радиуса не может быть выражен отрицательным числом. в) Нет, так как перед второй скобкой стоит знак «–». г) Да. 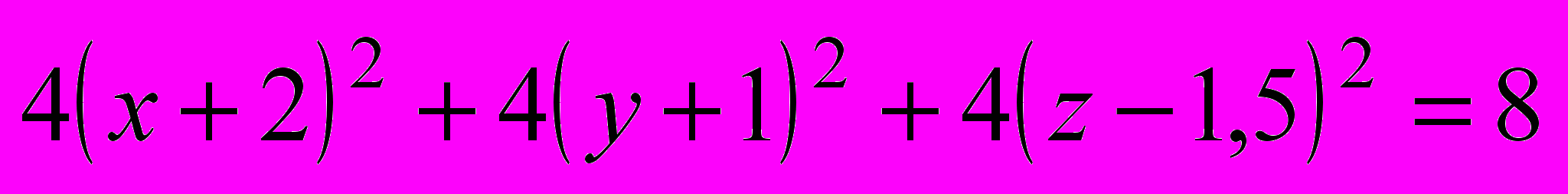 ; ;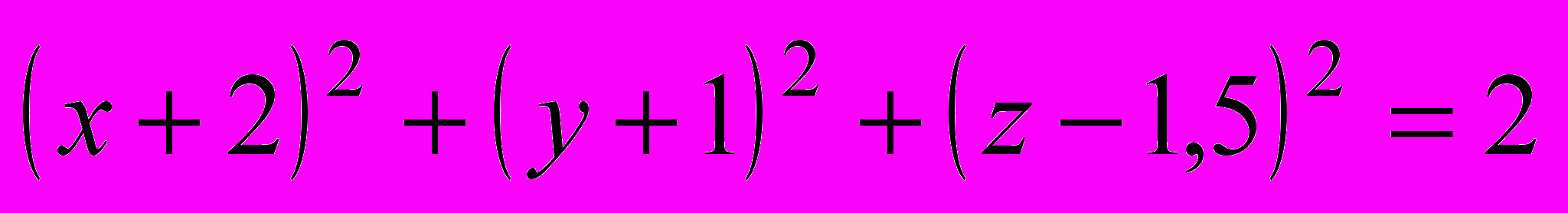 ; ;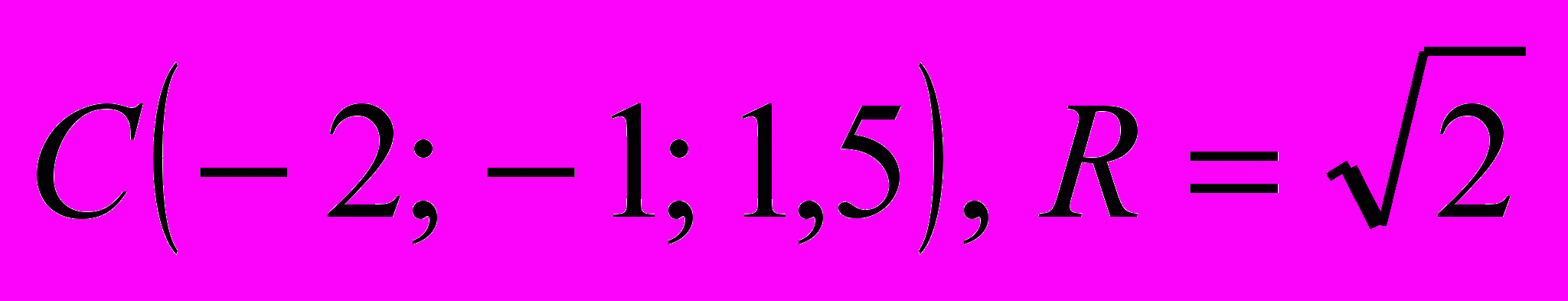 . . | Устная работа, упражне-ния | Доска с заранее написан-ными на ней урав-нениями | |
| 3 | На данном этапе осуществляется закрепление основных теоретических фактов, с которыми познакомились учащиеся на данном уроке. | | | | |
| 4 | В домашнее задание обязательно включается работа с теоретическим материалом и несложные задания по его применению. | | | | |
Приложение 7
