Методика решения текстовых задач в 5-6 классах Учитель математики

Вид материала

Содержание

Процентное отношение.
Типовые арифметические задачи.
1. Задачи на нахождение чисел по их сумме и разности.
2. Задачи на вычисление неизвестного по разности двух величин.
3. Задачи на исключение неизвестной величины путем вычитания.
Задачи на замену данных и предположение.
Задачи на движение.
Разные задачи.

Подобный материал:

1 2 3 4

Изменение величины в процентах.

Часто встречаются величины, значения которых меняются: производительность труда, заработная плата; цена товара, масса детали при обработке и т.д. Изменения величин принято характеризовать с помощью процентов.

Задача. Завод выпустил 884 трактора вместо 850 тракторов, намеченных по плану. На сколько процентов завод перевыполнил план?

Краткое условие:

План-100%, 850 тр.

Факт- 884 тр.

На какое количество тракторов завод выпустил больше, чем по плану? 884-850=34(тр)

Какой процент от плана составляет полученная разность? 34/850=2/50=4/100=4%

Ответ: завод перевыполнил план на 4 %

Вывод: чтобы узнать изменение величины в процентах, нужно узнать, на какое число единиц изменилась эта величина, а затем найти процентное отношение полученной разности к первоначальному значению величины.

Процентное отношение.

1. Решить задачу: «Расстояние между двумя селами 24км. За первую неделю бригада заасфальтировала 15 км. Какую часть всего расстояния заасфальтировала бригада за первую неделю?

Так как 24 км составляют целое, то 1 км составляет 1/24 от всего расстояния. По условию бригада заасфальтировала 15 км, следовательно, они составляют 15/24 всего расстояния, т.е. 5/8.

Решение задачи свелось к вычислению величины отношения числа заасфальтированной части к длине всего расстояния между селами.

2.Решим эту же задачу, но зададим другой вопрос: «Сколько процентов составляет заасфальтированная дорога от всего расстояния?

Для ответа достаточно полученное в предыдущей задаче отношение выразить в процентах. 5/8 = 62,5% Ответ: заасфальтированная дорога составляет 62,5% от всего расстояния.

Отношение, выраженное в процентах, называют процентным отношением.

Типовые арифметические задачи.

Если в задачах зависимости между заданными величинами сходны. То задачи являются аналогичными и ход их решения тоже аналогичны. Рассмотрим наиболее типичные зависимости величин, встречающиеся в задачах.

1. Задачи на нахождение чисел по их сумме и разности.

Перед решением задач такого типа можно решить задачу: «В двух пачках было 40 тетрадей. Сколько тетрадей было в каждой пачке, если в обеих пачках тетрадей было поровну?» Решение: 40:2=20(тет.) в каждой пачке.

Затем перейти к решению такой задачи: « В двух пачках было 40 тетрадей. Когда из первой пачки взяли 10 тетрадей, то в двух пачках тетрадей стало поровну. Сколько тетрадей было во второй пачке первоначально?

Рассмотрим два способа решения.

1 способ. Чтобы решить задачу как предыдущую, нужно уравнять количество тетрадей в пачках, «убрав» из первой пачки 10 тетрадей. 1) 40 – 10 = 30(тет.)

Теперь количество тетрадей в пачках стало одинаковым, общее число равно 30 тетрадям. В каждой пачке станет по 15 тетрадей, а это соответствует числу тетрадей во второй пачке. 2) 30 : 2 = 15(тет.) Ответ: во второй пачке первоначально было 15 тетрадей.

2 способ. Предположим, что во вторую пачку добавили 10 тетрадей. Тогда число тетрадей в пачках станет одинаковым, но общее количество увеличится и станет равным:

1) 40 + 10 = 50(тет.)

В каждой пачке окажется по 25 тетрадей, а это соответствует числу тетрадей в первой папке: 2) 50 : 2 = 25(тет.)

Узнаем, сколько тетрадей было во второй пачке: 3) 25 – 10 = 15(тет.)

Ответ: во второй пачке первоначально было 15 тетрадей.

План решения таких задач:

Уравняйте…
Измените ( увеличьте или уменьшите) …
Найдите одно из слагаемых, для чего…
Найдите второе число.

Задача: « Периметр прямоугольника равен 48см., длина на 4см. больше ширины. Найдите стороны прямоугольника».

Чтобы свести к способу решения предыдущей задачи, учащиеся, вспомнив понятие периметра прямоугольника, находят сумму двух смежных сторон.

2. Задачи на вычисление неизвестного по разности двух величин.

При решении таких задач необходимо выделить неизменное данное и те, которые изменились.

Задача 1: «Два велосипедиста отправились в поход. Двигаясь с одинаковой скоростью, один проехал за неделю 420км., другой- 450км., причем второй был в пути на 2 часа больше первого. Сколько часов находился в пути каждый велосипедист?»

Решение: Неизменное данное - скорость велосипедистов. Изменились - расстояние и время.

1) На сколько километров второй велосипедист проехал больше первого за два часа?

450 – 420 = 30(км)

2) Какова скорость движения?

30: 2 = 15(км/ч)

3) Сколько часов был в пути первый велосипедист?

420: 15 = 18(ч)

4) Сколько часов был в пути второй велосипедист?

28 + 2 = 30(ч)

Ответ: первый находился в пути 28 ч., второй- 30ч.

Задача 2: « Если бы школьник купил 11 тетрадей, то у него осталось бы 5 коп. А на 15 тетрадей у него не хватит 7 коп. Сколько денег было у школьника?

Не изменилось количество денег у школьника, а количество тетрадей и оставшихся (недостающих) копеек изменилось.

Денег стало на 12 коп больше (5+7). Это изменение произошло за счет увеличения тетрадей на 4 штуки. 1) 15-11=4(тет.)

Стоимость 4 тетрадей – 12 коп, определим стоимость одной тетради: 2) 12:4=3(коп)

Теперь ответим на вопрос задачи: 3) 11*3 + 5 = 38(коп) или 15*3 – 7 = 38(коп)

Ответ: у школьника было 38 коп.

3. Задачи на исключение неизвестной величины путем вычитания.

Задача 1. За телегу и тройку лошадей просят 155 руб., а за ту же телегу и одну лошадь – на 90 руб. меньше. Сколько стоит одна лошадь?

Решение:

Составим краткую запись условия задачи:

1 телега 3 лошади – 155 руб.

1 телега 1 лошадь – на 90 руб. меньше, чем

Сравним две строчки в краткой записи. Почему уменьшилась стоимость второй покупки? (Т. к. купили на две лошади меньше и стоимость уменьшилась на 90 руб.)

1) Определим стоимость одной лошади: 90 : 2 = 45(руб)

Ответ: одна лошадь стоит 45 руб.

Есть ли лишние данные? Какой вопрос можно поставить, чтобы потребовались все данные?

Задача 2. Разносчик продал одному покупателю 15 яблок и 10 апельсинов и получил с него 1 руб.20 коп, а другому 15 яблок и 15 апельсинов и получил с него 1 руб. 50 коп. Сколько стоит одно яблоко и один апельсин?

Решение:

Составим краткую запись условия задачи:

15 яблок 10 апельсинов – 1 руб. 20 коп.

15 яблок 15 апельсинов – 1 руб. 50 коп.

Стоимость второй покупки больше, т. к. купили больше апельсинов. На сколько больше купили апельсинов? 1) 15 – 10 = 5(ап.)

На сколько больше заплатили во второй раз? 2) 1 руб. 50 коп. – 1 руб. 20 коп. = 30 коп.

Сколько стоит один апельсин? 3) 30 : 5 = 6(коп.)

Зная стоимость одного апельсина и общую стоимость первой покупки, можно узнать, сколько стоили 15 яблок. 4) 1 руб. 20 коп. – 6 коп.* 10 = 60 коп.

Зная стоимость 15 яблок, можно узнать стоимость одного яблока. 5) 60: 15 = 4( коп).

Ответ: одно яблоко стоит 4 коп., один апельсин – 6 коп.

Задачи на замену данных и предположение.

При решении некоторых задач можно видоизменить условие задачи. Примеры таких задач приведены в учебнике математики 5 кл. под редакцией Г. В. Дорофеева, и. ф. Шарыгина в пункте «Разные арифметические задачи».

Задача 1. « Для детского сада купили 20 пирамид: больших и маленьких – по 7 и 5 колец. У всех пирамид 128 колец. Сколько было больших пирамид?

1 способ.

Решение: Предположим, что колец во всех пирамидах было поровну – по 5 колец. Сколько для этого нужно снять колец с каждой большой пирамиды?

1) 7 – 5 = 2 (кольца)

Сколько колец останется на всех 20 пирамидах?

2) 20*5 = 100 (колец)

Почему меньше чем в условии? Снимали кольца с больших пирамид. Сколько колец сняли?

3) 128 – 100 = 28 (колец)

Со скольких пирамид сняли по 2 кольца?

4) 28: 2 = 14 (пирамид) Ответ: было 14 больших пирамид.

2 способ.

Предположим, что колец во всех пирамидах было поровну – по 7 колец. Сколько для этого колец нужно добавить на каждую маленькую пирамиду?

1) 7 – 5 = 2 (кольца)

Сколько колец будет на всех 20 пирамидах?

2) 20*7 = 140 (колец)

Но в условии задачи дано 128 колец. Почему больше? На каждую маленькую добавили по 2 кольца. Сколько колец добавили?

3) 140 – 128 = 12 (колец)

На какое число пирамид добавили по 2 кольца?

4) 12:2 = 6 (пирамид) маленьких.

Всего 20 пирамид. Сколько больших пирамид?

5) 20 – 6 = 14 (пирамид ) больших. Ответ: было 14 больших пирамид.

В учебнике приведен 1 способ, более короткий. Но некоторые учащиеся сами могут предложить 2 способ. Почему мы только снимаем кольца, получив меньшие пирамиды? Можем получить большие, добавив по 2 кольца на меньшие?

Задачи на движение.

По содержанию задачи на движение различаются:

а) на встречное движение;

б) на движение в одном направлении.

Задача 1. Из некоторого пункта А отправились одновременно: а) в одном направлении; б) в противоположных направлениях

Пешеход со скоростью 5км/ч и велосипедист со скоростью 15км/ч. Какое расстояние будет между ними через 3 часа?

Решение.

С

хематический рисунок.

а)

15 км/ч

5км/ч

б)

15км/ч 5км/ч

1) Найдем скорость удаления пешехода и велосипедиста:

а) 15 – 5 = 10 (км/ч) б) 15 + 5 = 20 ( км/ч)

2) Зная скорость удаления. Можно найти расстояние между ними через 3 часа.

а) 10*3 = 30 (км); б) 20*3 = 60 (км). Ответ: а) 30км., б) 60 км.

Задача 2. Из пунктов А и В, расстояние между которыми 70 км., отправились одновременно пешеход и велосипедист со скоростями 5км/ч и 15км/ч соответственно. Какое расстояние будет между ними через 3 часа?

Решение.

Так как в задаче не указано, в каком направлении движутся велосипедист и пешеход, то рассмотрим четыре возможных случая.

а) Движение навстречу друг другу.

5км/ч 15км/ч

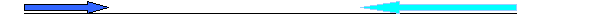
А В

70км

б) Движение в одном направлении.

5км/ч 15км/ч

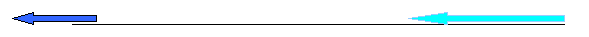
А В

70км

в) Движение в противоположных направлениях.

5км/ч 15км/ч

А В

70км

г) Движение в одном направлении.

5км/ч 15км/ч

А В

70км

В случаях а) и б) происходит сближение, поэтому нужно найти скорость сближения.

В случаях в) и г) пешеход и велосипедист удаляются друг от друга.

При решении задач на движение по реке есть особенность: приходится различать скорость движения по течению и скорость движения против течения.

Разные задачи.

1. Комбинаторные задачи.

Есть задачи, где требуется найти не один, а несколько вариантов ответа. Решая подобные задачи, приходится перебирать различные варианты, переставлять элементы, комбинировать их. Задачи такого типа называются комбинаторными.

Задача 1. «Сколько различных флагов можно сшить из материи трех цветов: красного, синего и белого, если каждый должен состоять из трех равных горизонтальных полос разного цвета?

Решение.

Вариантов решения этой задачи не очень много, поэтому их можно последовательно перебрать, нарисовав все возможные случаи.

К		К		С		С	Б	Б
С	Б	Б	К	С	К
Б	С	К	Б	К	С

Ответ: 6 различных цветов.

Задача 2. На фабрике выпускают двухцветные ручки со стержнями красного, фиолетового, синего и зеленого цвета. Как можно скомбинировать цвета стержней, чтобы в каждой ручке было два разных цвета?

Решение.

	Ф	К	С
Ф	-
К	КФ	-
С	СФ	СК	-
З	ЗФ	ЗК	ЗС	-

Ответ: КФ, СФ, ЗФ, СК, ЗК, ЗС.

Задача 3.Класс решил провести выборы старосты и его заместителя. В результате тайного голосования в первом туре победили: Федя, Катя, Сережа, Зоя. Сколько возможно вариантов выборов во втором туре?

Решение. Составим таблицу.

	Ф	К	С	З
Ф	-	ФК	ФС	ФЗ
К	КФ	-	КС	КЗ
С	СФ	СК	-	СЗ
З	ЗФ	ЗК	ЗС	-

Ответ: 12 вариантов.

Задача 4.У Пети есть 2 автомобиля, 4 оловяных солдатика и 2 мяча. Он хочет подарить набор из трех разных игрушек своему другу на день рождения. Оказалось, выбрать не так уж просто, слишком много получается вариантов, тем более, что все мячи, солдатики и машины такие непохожие. Сколько наборов мог составить Петя?

Решение.

Обозначим автомобили, солдатиков и мячи буквами с индексами: А1, А2, С1, С2, С3, С4, М1, М2. Построим граф- дерево. Точка Н- начало, от которой выставляем один из вариантов А1 и А2. От точки А1 можно выбрать уже 4 варианта солдатиков и так далее.

Н

А1

А 2

С4

С1

С2

С3

С1

С2

С3

С4

М1мммММММм

М2

М1 3 3 3 3 3 3 3 3 3

М2

М1

М2

М

1

М2

М1мммММММм

М2

М1 3 3 3 3 3 3 3 3 3

М2

М1

М2

М

1

М2

Двигаясь от начала по отрезкам вниз получим 16 вариантов.

Ответ: 16 наборов.

2. Задачи на делимость.

При решении многих задач полезно учитывать свойства делимости чисел, находить их НОК и НОД.

Задача 1. Трое выиграли некоторую сумму денег. На долю первого пришлось ¼ этой суммы, на долю второго- 1/7, а на долю третьего- 17 флоринов. Как велик выигрыш?

Решение. Если искомое число целое, то оно делится на 4 и на 7. НОК (4,7) = 28.

Следовательно, первый получит: 28:4 = 7 (фл.); второй получит: 28:7 = 4 (фл.), а третий оставшиеся 17 флоринов, что соответствует условию задачи.

Ответ: 28 флоринов.

Задача 2. Ученики 5 класса купили 203 учебника. Каждый купил одинаковое количество книг. Сколько было пятиклассников, и сколько учебников купил каждый?

Решение. Обе величины, которые требуется определить, должны быть целыми числами и находиться среди делителей числа 203; но: 203 = 1*7*29. В 5 классе не может быть 29 учебников. Значит это пятиклассников 29, и каждый купил по 7 учебников.

Ответ: 29 пятиклассников, каждый купил по 7 учебников.

3. Подбор и догадка при решении задач.

Иногда решение задачи обычным способом или очень сложно, или вообще невозможно. В таких случаях полезно рассмотреть различные варианты, и тогда на помощь может придти догадка. Здесь нужно уметь отобрать нужные и отбросить ненужные варианты.

Задача 1. Три школьных товарища купили 14 пирожков, причем Коля купил в 2 раза меньше Вити, а Женя - больше Коли, но меньше Вити. Сколько пирожков купил каждый товарищ?

Решение. Витя купил больше всех, значит, больше, чем третью часть от 14, то есть 5 или больше. Кроме того, число его пирожков делится на 2, следовательно, может быть: 6,8,10,12,14 пирожков. Возьмем наименьшее возможное, пусть Витя купил 6 пирожков, тогда Коля- 3, а Женя- 5пирожков, что удовлетворяет условию задачи, т.к. 6+ 3+5=14.

Другие значения не подходят.

Ответ: Витя 6 п., Коля 3 п., Женя 5 п.

Задача 2. Отец старше сына в 4 раза, через 20 лет он будет старше сына в 2 раза. Сколько лет отцу сейчас?

Решение. О возрасте отца известно, что он выражается числом, которое делится на 4. Начнем последовательность с числа20: 20, 24, 28, 32,…..

Составим таблицу по условию задачи:

	Через 20 лет.
Отец	Сын	Отец	Сын
20 24 28 32 36 40	5 6 7 8 9 10	40 44 48 52 56 60	25 26 27 28 29 30

Ответ: отцу сейчас 40 лет.

Задача 3. Разность двух чисел 70. Одно число больше другого в 11 раз. Найдите эти числа.

Решение. Выпишем пары чисел, одно из которых в 11 раз больше другого и их разности:

1и11, 11-1 = 10;

2и22, 22-2 = 20;

3и33, 33-3 = 30;

4и44, 44-4 = 40 и т. д.

Закономерность: разность равна целому числу десятков. Значит числу 70 будет соответствовать пара: 7 и 70.

4. Практические задачи.

Практические задачи внешне отличаются от привычных задач учебника. Решая их, учащиеся убеждаются, что знание математики очень пригодится в жизни.

№1. Как велик миллион?

а) Сколько потребуется комплектов ваших учебников, чтобы набралось миллион страниц? Сколько страниц во всех учебниках у всех ребят вашего класса?

б) Сможете ли вы отсчитать миллион зерен пшена?

Предлагается следующий способ подсчета:

- сосчитайте количество зерен в наперстке;

- наполните наперстками стакан;

- выясните, сколько стаканов вам понадобится.

в) Найдите вокруг себя миллион чего-нибудь.

Придумайте, что еще можно считать миллионами? Как вы думаете, результаты, которые вы получили, решая предыдущие задачи -точные или приближенные?

№2. Как можно подсчитать, сколько съедает ваше домашнее животное за день, за неделю, за год?

№3. Спланируйте куда - либо путешествие. Сколько оно будет стоить?

№4. Сколько стоит приготовить торт?

№5. Знаете ли вы себя?

Какой у вас рост, вес, размер одежды и обуви? Обувь какого размера носит большинство ребят из вашего класса? Как вы думаете, в соседнем классе распространен тот же размер или другой?

№6. Составьте план школы и сделайте модель вашего дома. Нарисуйте окрестности вашей школы?

В математике основным средством развития творческих способностей ученика является решение задачи, при этом основной целью должно являться не получение решения задачи (в смысле ответа), не получение результата решения, а само решение как метод, как процесс, как совокупность логических шагов, приводящих к получению ответа. При этом важно научить ученика (осознанно или не осознанно) применять известные эвристические приемы. Большой обучающий эффект дает решение задачи разными способами, а также составление новых задач как констатация факта полного овладения методом решения не только этой задачи, но и класса таких задач, получаемых из исходной путем трансформации условия.

Главная цель обучения - приобретение обобщающих стратегий. Надо учить учиться.

Песталоцци считал, что одной из главных целей обучения является развитие умственных и духовных сил ребенка.

Список литературы

1.Виноградова Л.В., Тиликайнен В.Е. Задачи на нахождение дроби от числа и числа от дроби // Ж. Математика в школе. – 1999. - №4.

2.Волович М.Б. Ключ к пониманию математики. 5-6 класс. – Москва: Аквариум, 1997.

3.Газарян Р. Задача, как обучающая модель // Г. Математика. – 2003. - №11. – С.1-3.

4.Герасимова А.Д. Ориентировочная основа задач // Ж. Математика в школе. – 2003. - №6. – С.40-42.

5.Демидова Т.Е., Тонких А.П. Алгебраический метод решения текстовых задач для нахождения арифметического способа их решения // Ж. Начальная школа. – 2001. - №3. – С.100-104.

6.Епишева О.Б., Крупич В.И. Учить школьников учиться математике. – Москва: Просвещение, 1990.

7.Жохов В. Преемственность в обучении между начальной и средней школой // Г. Математика. – 2003. - №21. – С.33-35.

8.Мамыкина М.Ю. Работа над задачей // Ж. Начальная школа. – 2003. - №4. – С.63-67.

9.Овсиенко Г.В. Больше внимания арифметическим задачам // Ж. Математика в школе. – 1997. - №1. – С.16-17.

10. Столяр А.А,Черкасов Р.С.,. Методика преподавания математики в средней школе. – Москва: Просвещение, 1985.

11.Ремшмидт Х. Подростковый и юношеский возраст: Проблемы становления личности. – Москва: Мир, 1994. – 319 с.

12. Формирование приемов математического мышления / Под ред. Талызиной Н.Ф. – Москва: Вентана-Граф, 1995.

13.Тричикова Л.А. Активация познавательной деятельности учащихся при работе над простой задачей // Ж. Начальная школа. – 1995. - №10. – С.24-29.

14.Устинова Э.В. Программа организации адаптационного периода учащихся пятых классов муниципального образовательного учреждения // Завуч начальной школы. – 2003. - №5. – С.99-105.

15.Фонин Д.С., Целищева И.И. Моделирование, как важное средство обучения решению задач // Начальная школа. – 1990. - №3. – С.33-37.

16.Хуторской А.В. Формы, методы и приемы обучения // Практикум по дидактике и современным методикам обучения: Питер, 2004. – С.373-533.

17.Царева С.Е. Различные способы решения текстовых задач // Ж. Начальная школа. – 1991. - №2. – С.78-84.

18.Царева С.Е. Обучение решению задач // Ж. Начальная школа. – 1998. - №1. – С.102-107.

.

Blog

Методика решения текстовых задач в 5-6 классах Учитель математики

Содержание