Учебно-методический комплекс обсужден на заседании кафедры «Математика и информатика» «18» ноября 2007 г. (Протокол №7)
| Вид материала | Учебно-методический комплекс |
- Учебно-методический комплекс обсужден на заседании кафедры «Математика и информатика», 778.25kb.
- Учебно-методический комплекс Рабочая учебная программа для студентов одо и озо специальности, 586.96kb.
- Учебно-методический комплекс Рабочая учебная программа. Методические указания по выполнению, 331.05kb.
- Учебно-методический комплекс обсужден и рекомендован к изданию на заседании кафедры, 481.7kb.
- Учебно-методический комплекс обсужден на заседании кафедры «Экономика и менеджмент», 710.92kb.
- Учебно-методический комплекс обсужден на заседании кафедры «Экономики и менеджмента», 4784.46kb.
- Учебно-методический комплекс обсужден на заседании кафедры «Философия и политология», 8372.98kb.
- Учебно-методический комплекс по дисциплине «промышленный маркетинг» Учебное пособие, 1440.18kb.
- Учебно-методический комплекс по дисциплине «маркетинговые иследования» Учебное пособие, 1390.13kb.
- Учебно-методический комплекс по дисциплине «мерчендайзинг» Программа и методические, 326.86kb.
Случайное событие, которое может произойти или нет.
Вероятность случайного события находится в промежутке (0,1).
Американский инженер Р. Хартли в 1928г. для измерения количества информации предложил формулу выбора одного сообщения из равновероятных сообщений (событий):
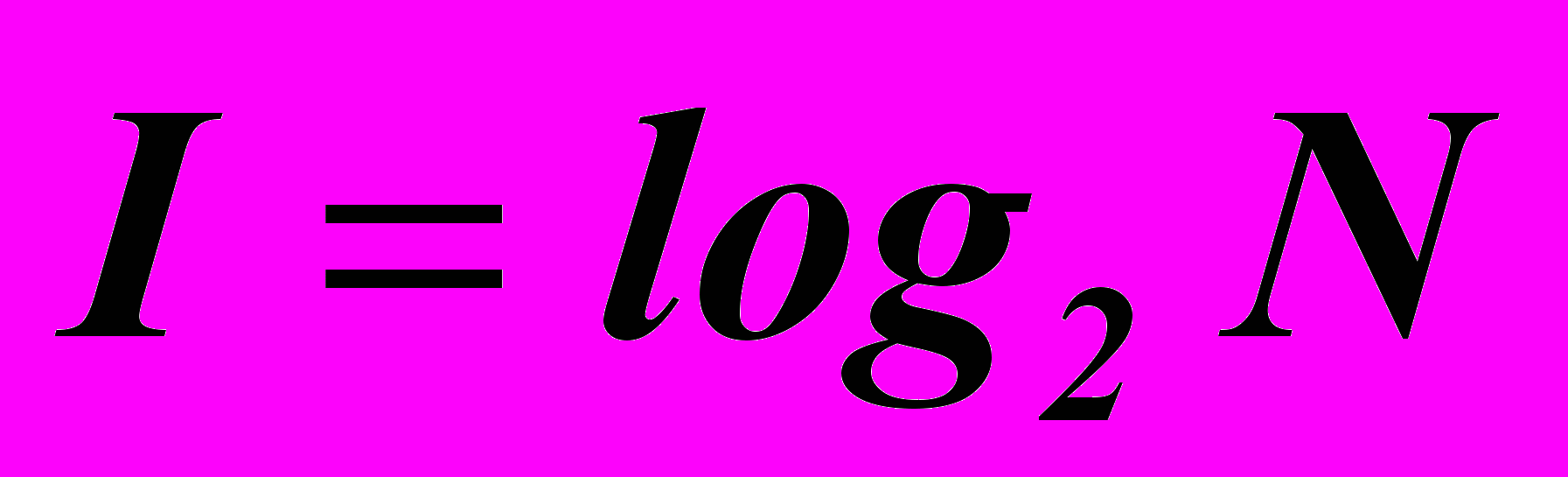 ,
,
где I – количество информации; N – количество сообщений.
Например, при N=2 количество информации I=1.
Если вероятность сообщений (событий) разная, то мы имеем формулу, которую в 1948г. преложил американский ученый К. Шеннон:
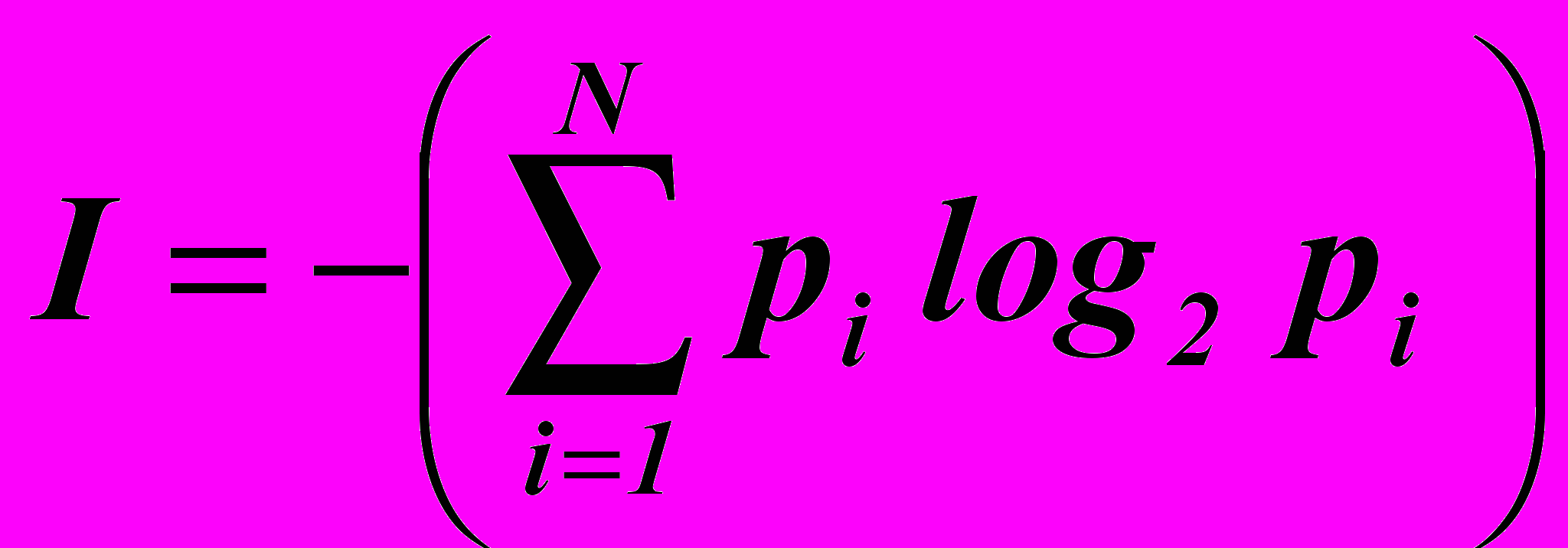 ,
,где pi – вероятность того, что именно i-е сообщение выделено из N сообщений.
Если вероятности р1,...,рN равны 1/N, то формула Шеннона превращается в формулу Хартли.
Если вероятность события равна 1(т.е. оно достоверно), то количество информации равно 0.
Если вероятность наступления какого-либо события одинакова, т.е. равна ½, то количество информации, которое несет с собой событие равно 1.
Эта и есть основная единица информации – бит.
1 Байт – 8 бит. (в 8 разрядах 00000000-11111111 можно записать 256 целых двоичных чисел).
Таким образом, байт может соответствовать закодированному символу алфавита или любому другому символу. Байт составляет основу кодировок в компьютере (ASCII-кодов (используемый в MS DOS, UNICODE в Windows).
1 Килобайт (Кбайт) – 1024 байт.(210 байт)
1 Мегабайт (Мбайт) – 1024 Кбайт.
1 Гигабайт (Гбайт) – 1024 Мбайт.
Системы счисления.
Система счисления (СС)- это способ наименования и обозначения чисел. Наиболее известные СС – римская и позиционная (например, десятичная).
Римская СС служит для количественного обозначения (II,V,XI,…).
Позиционная СС (ПСС) – это СС, в которой числовое значение цифры зависит от ее места в записи числа. Основанием подобной системы может быть любое натуральное число.
Для представления информации в компьютер используется двоичная система счисления. Это информация из 0 и 1. Любое, привычное нам, десятичное число можно представить двоичным и наоборот.
Например, 310 =1012 ; 210 = 102 .
Любое десятичное число можно представить, например:
326=3*102+2*101+6*100.
Аналогично любое двоичное число можно представить, например:
10111=1*24+0*23+1*22+1*21+1*20.
Если сложить последнюю сумму получим: 8+0+4+2+1=15.
Т.е. 101112=1510.
В общем виде двоичное число равно a1a2…an=
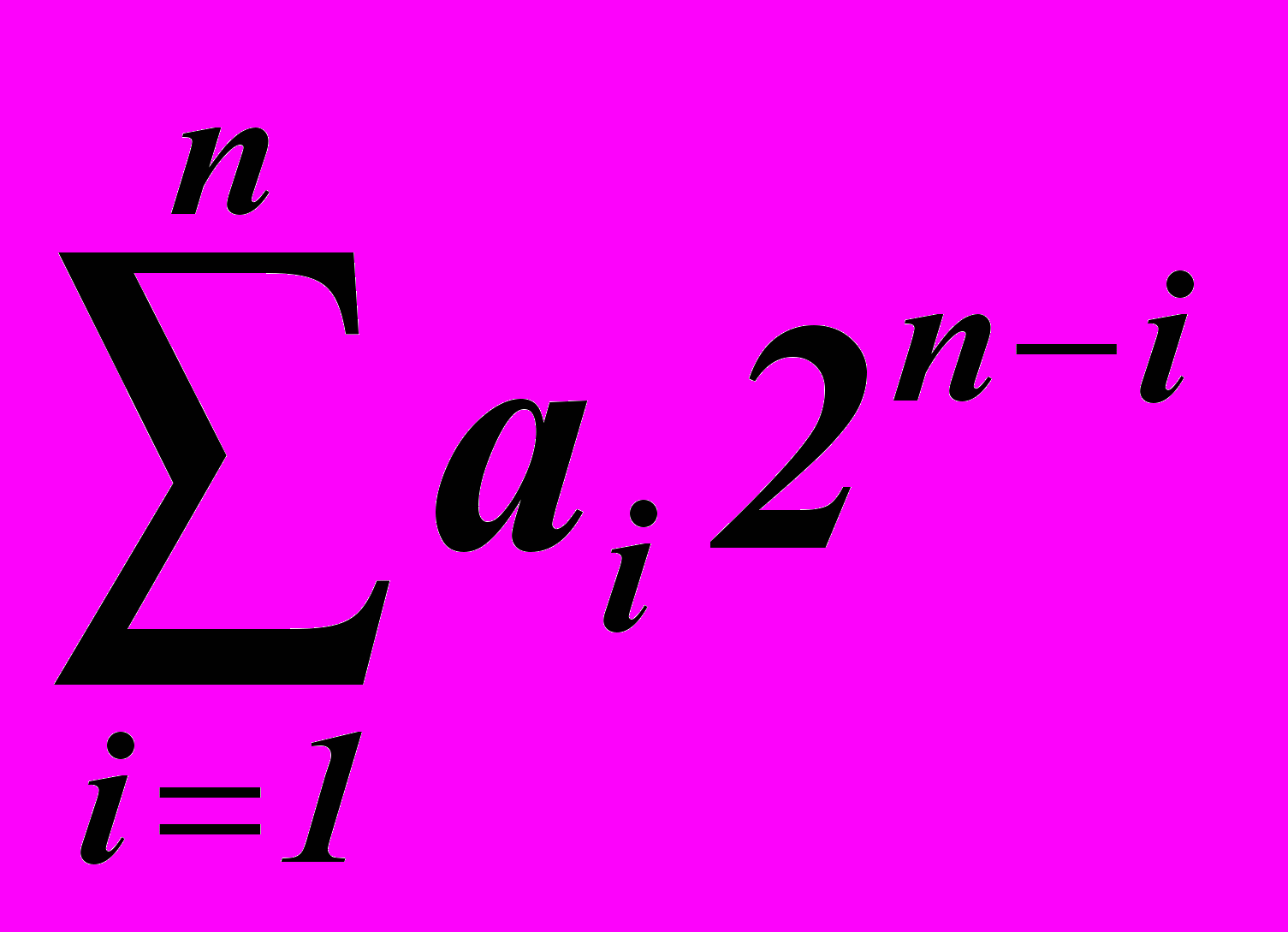 , т.е. соответствует десятичному числу, вычисленному из последней суммы
, т.е. соответствует десятичному числу, вычисленному из последней суммы (a1 ,a2, …, an – позиции двоичного числа, начиная со старшего разряда).
Из десятичного двоичное можно получить делением на 2, и каждый остаток от деления будет от младшего разряда к старшему составлять двоичное число.
Например:
13/2
1 6/2 Результат: 1310 = 11012
0 3/2
1 1
Кроме этих систем счисления используются 8-ричные и 16-ричные СС.
В 16-ричной СС основанием является F, т.к. цифры обозначения используются следующие: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E.
ИНФОРМАЦИЯ В ТЕХНИЧЕСКИХ УСТРОЙСТВАХ И СИСТЕМАХ
О
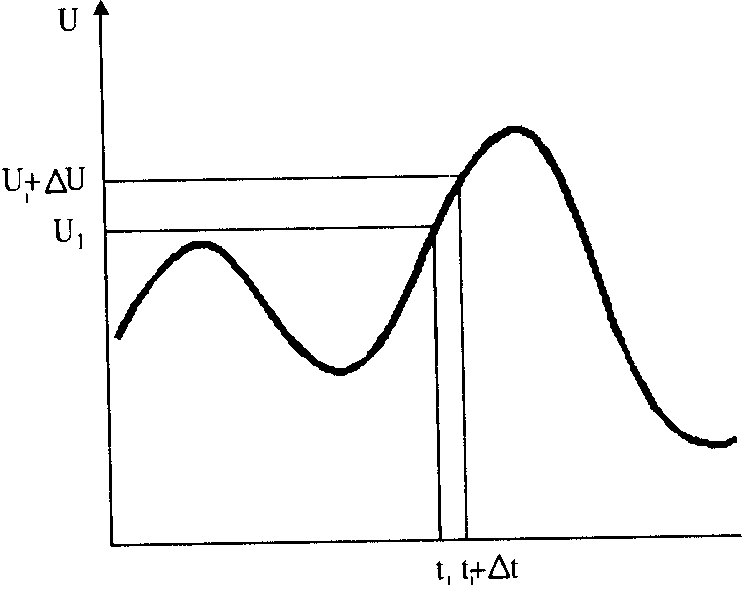
Непрерывный сигнал
бмен информацией происходит не только среди людей. Современная жизнь не представляется без различных устройств и машин, которые облегчают работу и заменяют человека при выполнении многих задач. Между тем работа машин невозможна без процессов обработки информации.
В технических устройствах и системах прием, обработка и передача информации осуществляется с помощью сигналов. Сигналы отражают физические характеристики изучаемых объектов и процессов. Посредством сигналов информация может передаваться на короткие большие расстояния. Информация в виде сигнала может различным образом перерабатываться, сохраняться, уничтожаться и т. п. Различают несколько видов сигналов: звуковые, которые можно слышать при работе милицейской сирены; световые, передающие информацию от пульта дистанционного управления к телевизору, а также электрические. При передаче информации посредством электрического сигнала значение информации выражается в параметрах электрического тока — в силе тока и напряжении.
Существующие в технических устройствах сигналы делятся на непрерывные (или аналоговые) и дискретные.
Непрерывность сигнала означает возможность его изменения на любую малую величину в любой заданный малый промежуток времени (см. выше рис.).
Образование аналогового сигнала происходит, например, при получении первичной информации с датчиков, связанных с изучаемым объектом или внешней средой. Полученный сигнал обычно требует дальнейшей его обработки. Это может быть передача, преобразование или сохранение.
Продемонстрировать аналоговую обработку сигнала можно, рассматривая процесс преобразования сигнала, идущего от микрофона к динамику. Микрофон преобразует звуковой сигнал в слабый электрический, выходной характеристикой которого является напряжение.
Микрофон и динамик применяются для усиления звукового сигнала. Для этого целенаправленное усиление аналогового электрического сигнала до требуемой величины. Получив, таким образом, необходимый сигнал, динамик его преобразовывает в более сильный звуковой.
Примером аналоговой передачи сигнала является передача речи по телефонным проводам: речевая информация преобразуется в аналоговые электрические сигналы, которые по проводам передаются абоненту, а затем обратно преобразуются в речевую информацию. Аналоговое сохранение информации является также довольно распространенным явлением. Это, например, запись звукового сигнала на магнитный носитель.
До семидесятых годов XX века технические устройства работали только с аналоговыми сигналами. Аналоговыми являлись и способы их обработки.
С появлением в семидесятых годах XX века микропроцессора — основного элемента ЭВМ, а также микросхем с высокой степенью интеграции стали получать распространение дискретные и цифровые сигналы и соответствующие способы их обработки.
Дискретность сигнала означает возможность его измерения только на конечном отрезке, в строго определенные моменты времени, т.е. сам сигнал представляет собой не непрерывную функцию, а последовательность дискретных значений (см. рис.).
Д
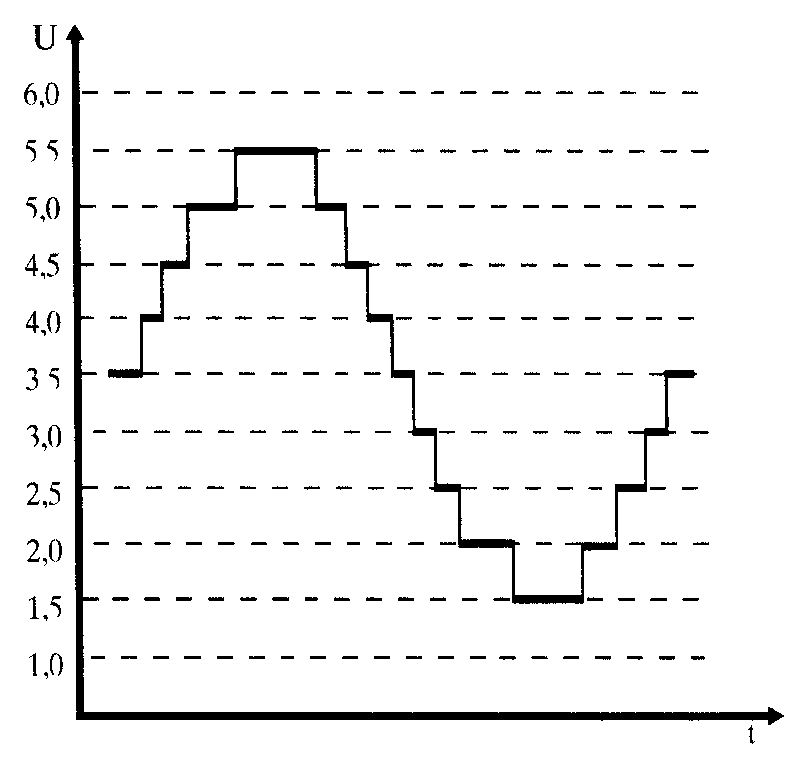
Цифровой сигнал
искретные значения функции, полученные в дискретные моменты времени, имеют приближенные числовые значения. В случае, когда наличие приближенных значений не удовлетворяет поставленной задаче, производят округление имеющихся значений с заданной степенью точности. И тогда уже вместо приближенных значений получаются определенные конечные числовые значения.
Дискретный сигнал, значения которого выражены определенными конечными числами, называется цифровым.
Для обработки, хранения, передачи цифровых сигналов также существуют специальные технические устройства. Бурное развитие вычислительной техники, средств телекоммуникации непосредственно связано с обработкой именно цифровых сигналов, поскольку цифровая связь имеет множество преимуществ по сравнению с аналоговой.
Широкое применение цифрового способа хранения информации находит запись различного рода информации на аудио- и видеокомпакт-дисках (CD-ROM).
С цифровой передачей данных мы сталкиваемся при обмене информацией между компьютерами с помощью модема или при работе с факсимильными средствами связи.
Несмотря на то что цифровая обработка информации приобретает все большее распространение, отказаться от аналоговой невозможно. Еще остается достаточно много систем и устройств, в которых информация может передаваться только в виде аналогового сигнала. В связи с этим решаются различные вопросы, ищутся способы преобразования аналогового сигнала в цифровой и наоборот.
При преобразовании исходного аналогового сигнала в цифровой появляется определенная погрешность. Но, уменьшая шаг по оси времени и функции сигнала, можно достичь уменьшения погрешности. Использование современных высокоскоростных технических средств обработки и хранения цифровых сигналов позволяет значительно упростить и удешевить процесс преобразования аналогового сигнала в цифровой. А также устранить недостатки, присущие аналоговой передаче сигнала, например влияние шумов. В результате даже такие традиционные области использования аналоговых сигналов, как телефонная связь и радиовещание, переходят на цифровую форму обработки и передачи сигналов.
Этот процесс получил наибольшее развитие с появлением глобальных компьютерных сетей.
Таким образом, мы рассмотрели существующие виды информации. Зрительная и звуковая, посредством которой общаются люди, а также информация в виде сигналов непосредственно связаны между собой. Преобразования информации из одного вида в другой показывают, насколько важен и непрерывен процесс обмена информацией. Применение технических устройств делает этот процесс неотъемлемой частью нашей жизни.
Вопросы по теме лекции 1:
Вещественно-энергетическая и информационная картины мира.
- Информация как мера упорядоченности в неживой природе.
- Информация и энтропия.
- Информационные процессы в живой природе, обществе и технике: получение, передача, преобразование, хранение использование информации.
- Информационные процессы в управлении. Системы с обратной связью.
- Информация и знания.
- Количество информации как мера уменьшения неопределенности знаний. Единицы измерения количества информации.
- Кодирование информации с помощью знаковых систем.
- Естественные и искусственные языки.
- Двоичное кодирование информации.
- Кодирование аналоговой (непрерывной) графической и звуковой информации методом дискретизации.
- Системы счисления. Позиционные и непозиционные системы счисления. Двоичная система счисления. Двоичная: арифметика. Системы счисления, используемые в компьютере.
Лекция 2. Основы логики и логические основы компьютера
Основные понятия математической логики
Существуют высказывания, которые можно проверить, истинны они или ложны. Операции над подобными высказываниями относятся к классической математической логике. Математическая логика включает математические методы исследования способов рассуждений и умозаключений. Будем обозначать результат истинного высказывания «Т» (true – истина), результат ложного высказывания «F» (false – ложь). Высказывания будем обозначать латинскими буквами (А, B, C, D и т.д.).
Рассмотрим основные операции над высказываниями. Приведем их в таблице 2.5.
Таблица 2.5
Основные операции исчисления высказываний
| № п/п | Наименование операции и краткий смысл | Высказывания | Запись операции | Результат операции | |
| А | В | ||||
| 1. | Конъюнкция (соединение двух высказываний в одно: логическое «и») | T T F F | T F F T | A&B | T F F F |
| 2. | Дизъюнкция (соединение двух высказываний в одно: логическое «или») | T T F F | T F F T | А  В В | T T F T |
| 3. | Импликация (общее высказывание, заключающееся в следовании одного высказывания из другого): А (посылка) влечет (имплицирует) В (заключение) | T T F F | T F F T | А  В В | T F T T |
| 4. | Логическое отрицание | T F | - - |  A A | F T |
Для иллюстрации использования операций над высказываниями при решении логических задач приведем примеры:
1). А= «T», B= «F». Чему равно логическое выражение:
(А
 В)&(
В)&( B)
B) A=? .
A=? .Решение: «T»&«T»
 «T» = «T», т.е. логическое выражение истинно.
«T» = «T», т.е. логическое выражение истинно.2). А&В= «T», С=«F». Чему равно логическое выражение:
((A
 C) &(C
C) &(C
 B))
B))  C
C A=?.
A=?. Решение: («F»&«T»)
 «F»
«F» «T» = «F»
«T» = «F» «F»
«F» «T» = «T», т.е. логическое выражение истинно.
«T» = «T», т.е. логическое выражение истинно.3). А=«Маша любит Петю»=«Т», B=«Петя не студент»=«Т», С= «Маша любит студента» - «F». Чему равно логическое выражение: A&B
 С=? .
С=? .Решение: («T»&«T»)
 «F» = «Т». То есть высказывание не верно, а верно A&B
«F» = «Т». То есть высказывание не верно, а верно A&B
 С= «Маша не любит студента».
С= «Маша не любит студента».Частью математической логики является булева алгебра. В ней имеем дело вместо «ложь» и «истина», соответственно, с операциями над «0» и «1». Булева алгебра названа в честь немецкого ученого Дж. Буля, разработавшего аппарат символической логики (1847-1854гг.).
Основные понятия теории множеств. Операции над множествами
Множество – это набор, совокупность каких либо объектов, называемых его элементами, обладающими общими для них всех характеристическими свойствами. По определению Г. Кантора: «Множество – есть многое мыслимое как единое». Это соответствует определению системы с точки зрения кибернетики.
Если класс объектов, на которых определяются любые множества обозначить U (Универсум), то любое рассматриваемое множество А принадлежит этому множеству, т.е. А
 U. Если рассматривать множества как области на поверхности или в пространстве, то элементами этих множеств могут служить бесконечное множество точек {x}, принадлежащих некоторой области (множеству). Часто оперируют со счетными множествами, состоящими из конечного числа элементов. Понятия таких множеств дают в начальных классах школы. Действия над счетными множествами и множествами, состоящими из бесконечного числа элементов (точек) аналогичны.
U. Если рассматривать множества как области на поверхности или в пространстве, то элементами этих множеств могут служить бесконечное множество точек {x}, принадлежащих некоторой области (множеству). Часто оперируют со счетными множествами, состоящими из конечного числа элементов. Понятия таких множеств дают в начальных классах школы. Действия над счетными множествами и множествами, состоящими из бесконечного числа элементов (точек) аналогичны. Основными операциями над множествами являются объединение, пересечение и дополнение.
| х   Рис.2.9 |
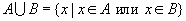 .
.Элементы {х}, входящие в объединение множеств A и B отображены в заштрихованной области на рисунке 2.9.
 Рис.2.10. |
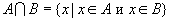 .
.Элементы х, входящие в пересечение множеств A и B отображены в заштрихованной области на рисунке 2.10.
 Рис. 2.11. |
 .
.Элементы х, входящие в дополнение В множества A отображены в заштрихованной области на рисунке 2.11.
 Рис. 2.12. |
а). Найти множество С, представляющее собой дополнение между
 до
до  ? Иначе говоря, С =
? Иначе говоря, С =  . Результат можно увидеть на рисунке 2.12. Множество элементов {x}, принадлежащих заштрихованной области, образуют искомое множество С.
. Результат можно увидеть на рисунке 2.12. Множество элементов {x}, принадлежащих заштрихованной области, образуют искомое множество С.б). Найдем аналогичное множество С =
 , где А={1,2,3,4,f,g}, B={4,g,f,5,6,7}. Результат С={1,2,3,5,6,7}.
, где А={1,2,3,4,f,g}, B={4,g,f,5,6,7}. Результат С={1,2,3,5,6,7}.Вопросы по теме лекции 2:
Основы логики. Основные понятия формальной логики.
- Алгебра высказываний.
- Базовые логические функции, логические законы и правила преобразования логических выражений.
- Построение таблиц истинности логических выражений.
- Логические схемы основных устройств компьютера (сумматор, регистр).
Лекция 3. Алгоритмизация и программирование
ФОРМЫ ЗАПИСИ АЛГОРИТМОВ
Существуют множество различных форм записи алгоритмов. Это связано с тем, что каждый исполнитель алгоритмов "понимает" лишь такой алгоритм, который записан на его "языке" и по его правилам. Условно выделяют 4 формы записи алгоритмов:
1. Словесно-пошаговая (текстовая).
2. Табличная.
3. Запись на алгоритмическом языке .
4. Графическая форма записи (Блок-схема).
Запись всякого алгоритма начинается с заголовка.
СЛОВЕСНО - ПОШАГОВАЯ (ТЕКСТОВАЯ)
Алгоритм записывается в виде пронумерованных этапов его выполнения. Например:
Алгоритм сложения двух чисел ( a и b ).
1. Спросить, чему равно число a .
2. Спросить, чему равно число b .
3. Сложить a и b, результат присвоить с.
4. Сообщить результат с.
ТАБЛИЧНАЯ ФОРМА ЗАПИСИ
Это запись алгоритма в виде таблицы. Используемые таблицы могут быть различными.
Для примера будем использовать упрощенную форму.
Порядок составления табличных алгоритмов:
1. Переписать выражение так, как допустимо в информатике.
2. Определить порядок действий.
3. Ввести обозначения промежуточных результатов.
4. Занести полученные действия в таблицу.
Пример:
Алгоритм вычисления R=2a +3b .
| № действия | действие | величина | результат | |
| 1 | 2 | |||
| 1 | * | 2 | a | |
| k | 2 | * | 3 | |
| b | u | 3 | + | |
| k | u | R | | |
ЗАПИСЬ НА АЛГОРИТМИЧЕСКОМ ЯЗЫКЕ
Это запись алгоритма на специальном языке (в том числе и на языке программирования).
Она осуществляется, строго следуя правилам того или иного алгоритмического языка.
Заголовок включает в себя название алгоритма, имена исходных данных (это величины, без которых выполнить алгоритм невозможно) и имена результатов (это величины, значения которых вычисляются в алгоритме).
Для указания начала и конца алгоритма используются служебные слова нач и кон.
Между ними записывают одну или несколько команд алгоритма, их называют тело алгоритма. Например:
Алгоритм вычисления значения выражения Y=z-a+2b.
| алг ВЗВ Y=z-a+2b арг z,a,b рез Y нач Y:= z - a + 2 * b кон | <- название алгоритма <- исходные данные (аргументы) <- результат <- начало алгоритма <- тело алгоритма <- конец алгоритма |
ГРАФИЧЕСКАЯ ФОРМА ЗАПИСИ (БЛОК-СХЕМЫ)
Алгоритм записывается в виде схемы, состоящей из Блоков (геометрических фигур) с размещенными в них действиями.
Блоки соединяются стрелочками и показывают структуру всего алгоритма.
Алгоритм в виде Блок-схемы начинается Блоком «начало» и заканчивается Блоком «конец».
Основные Блоки
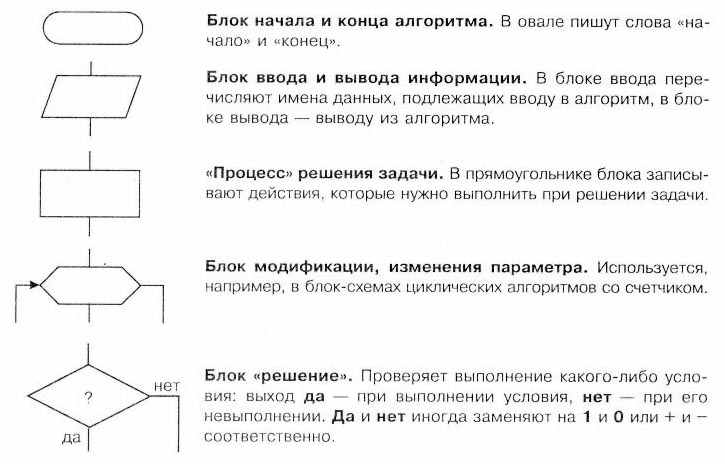
При составлении Блок-схемы алгоритма сначала выделяют исходные данные (все переменные величины после знака равенства и в условии) и результат (величины которые необходимо найти). Если в задании подразумеваются, но не указываются имена величин, то они обозначаются самостоятельно.
ОСНОВНЫЕ ЯЗЫКИ ПРОГРАММИРОВАНИЯ
Набор команд компьютера, описывающий процесс выполнения алгоритма называется программой.
Алгоритм для решения задачи с помощью компьютера может состоять из следующих шагов:
- формулировка решаемой задачи;
- формулирование логической или математической модели данной задачи;
- выражение этой модели в терминах определенной программы;
- выполнение программы на компьютере;
- проверка результатов для определения правильности решения.
Для успешного решения задачи компьютером все шаги алгоритма должны быть тщательно разработаны.
Составление алгоритмов – основа программирования. Исследования ученых в области анализа основных структур эффективных алгоритмов показывают , что особое внимание нужно обращать на фазу проверки, т.к. это самая решающая фаза при решении любой задачи на компьютере.
Для реализации алгоритмов на компьютере разработаны различные языки программирования.
Языки программирования подразделяются на языки:
- низкого уровня (на уровне кодов компьютера);
- высокого уровня (на уровне макрокоманд).
К языкам программирования низкого уровня относят:
- машинный язык;
- мнемокоды;
- автокоды.
Программа, написанная на машинном языке, представляет из себя последовательный набор кодов операций, адресов данных, хранящихся в памяти машины (компьютера). Машинный язык содержит много специфических моментов и любая программа состоит из большого числа отдельных команд. Написание программы на машинном языке требует много времени, даже у опытного программиста, а отладка программы требует много машинного времени.
Для улучшения методов работы на ЭВМ были созданы мнемокоды, отличающиеся от обычного машинного языка мнемоническим сокращением кодов операций, а также представлением адресов в форме символов. Мнемокодная программа вводилась в машину через внешние носители информации (перфокарты или перфоленту) и обрабатывалась с помощью Ассемблера.
Ассемблер – это программа, которая воспринимает входную информацию, записанную на мнемокоде, и переводит ее в программу, записанную на машинном языке.
Хотя мнемокод представляет собой шаг вперед по сравнению с машинным кодом, но один из серьезных недостатков его – это то, что он пригоден лишь для определенной машины.
Автокод – это совокупность команд для выполнения специализированных задач. Программа написанная на автокоде может использоваться на других машинах. Однако программирование в автокоде ведет к потере эффективности при выполнении работ.
Для повышения эффективности работ, уменьшения времени при отладке, совместимости программ и их наглядности были созданы языки программирования высокого уровня.
К идеальному языку высокого уровня предъявляются следующие требования:
- он должен способствовать полному использованию мощности машины;
- быть близок к естественному языку, на котором описывается задача;
- предоставлять возможность экономной записи задачи;
- позволять работать на любом компьютере и в любой операционной системе.
Одним из достаточно удовлетворительных языков высокого уровня в 60-х годах в нашей стране стал Алгол-60, который приспособлен главным образом к решению вычислительных задач. Возможность использования его для других классов задач обеспечивалась путем включения в программы процедур-кодов; за счет чего терялась машинная независимость программ. Одно из крупных неудобств Алгола-60 – это отсутствие аппарата для ввода и вывода информации в машине, предоставляющие возможность создания такого аппарата каждому разработчику транслятора. Это привело к появлению большого числа версий Алгола. Все это привело к тому, что в
70-х годах Алгол-60 был почти повсеместно вытеснен Фортраном. Это можно было заметить на изменении учебных программ во многих ВУЗах.
Фортран располагает вполне удовлетворительными средствами для ввода и вывода, логически он значительно проще Алгола. Но как Алгол, он приспособлен для решения вычислительных задач. Ценной особенностью Фортрана является предоставляемая им возможность совместного использования программ. Фортран-программой может обрабатываться табличная информация, однако специальных средств для описания таких процессов язык не имеет.
Язык Кобол приспособлен для решения задач, требующих переработки табличной информации. Таких как обработка данных, решение некоторых информационных задач. Однако в остальном он уступает Алголу и Фортрану.
На вычислительных комплексах в 80-х годах большое распространение получил алгоритмический язык ПЛ/1. Он объединяет в себе положительные черты предыдущих языков и имеет некоторые дополнительные возможности, в отличии от этих языков. Он допускает блочную структуру программ, позволяет обрабатывать как числовую информацию, так и структуры (т.е. табличную информацию), хорошо приспособлен для обработки текстовой информации. ПЛ/1 допускает совместное использование программ. Сложность его соизмерима со сложностью Алгола и Фортрана.
На персональных компьютерах появились такие проблемно-ориентированные языки высокого уровня, как Бейсик, Паскаль, Си. Первоначально они разрабатывались для операционной системы DOS. В Window's появились их оболочки – условно-событийного программирования: Vision Basic, Delphi, Vision C++. К объектно-ориентировванным языкам программирования относится VBA и DELPHI. Они позволяют активизировать объекты (т.е. запустить программу или программный код) путем оценки событий (нажата ли кнопка мыши, есть ли фокус при наведении мыши и др.). Эти языки являются оболочками к наиболее простым в программировании технических, графических и мультимедийных задач является Бейсик.
Вопросы по теме лекции 3:
Понятие алгоритма, свойства алгоритма.
- Исполнители алгоритмов. Система команд исполнителя. Способы записей алгоритмов. Формальное исполнение алгоритмов.
- Основные алгоритмические структуры (линейная, ветвление, выбор, цикл). Вспомогательные алгоритмы.
- Алгоритмическое программирование: основные типы и структуры данных, (переменные, массивы).
- Процедуры и функции.
- Объектно-ориентированное программирование.
- Объекты: свойства и методы.
- Событийные и общие процедуры.
- Графический интерфейс: форма и управляющие элементы.
Лекция 4. Моделирование и формализация
Понятия о моделях
Моделирование – это представление одного явления с помощью другого явления.
Впервые термин «модель» был употреблен в 1739 г. в энциклопедическом словаре в Германии. Слово «модель» стало широко использоваться в научной литературе в конце XIX века. Под моделью понимают отражение одного объекта другим объектом или отображение одной вещи другой вещью.
Общая классификация моделей в естествознании и технике следующая:
А.Материальные модели
1.Геометрические (карта, глобус)
2.Физические модели (градусник, часы)
Б Идеальные модели
1. Модели представления
2. Знаковые модели
3. Теоретические модели
4. Математические модели
Деление моделей по характеру воспроизводимых сторон оригинала
1. Субстанциональные модели: модельные соединения, эталонные вещества, биологические ткани в искусственной среде.
2. Структурные модели Сходные с оригиналом по внутреннему строению.
Модель изоморфна оригиналу. Пример модель бензола и других химических соединений.
3. Функциональные модели
Сходны с оригиналом только по свойствам: модель идеального раствора как идеального газа.
Внутренняя структура может быть известна - гетероморфные модели и неизвестна по сути, как "черный ящик" - метаморфная модель.
Перевод моделей из функциональных в изоморфные важная задача.
Субстанционные модели - это моделирование изучаемого объекта таким же объектом. Существует целый ряд пограничных моделей, которые занимают промежуточное положение между субстантивными и математическими моделями. Такие модели осуществляются в виде виртуальной реальности.
Математические модели - это отображение объекта с помощью системы уравнений. Любое уравнение-это математическая модель.
sin2x + cos2x = 1 - уравнение колебательного движения.
Принцип математического моделирования основан на конечном числе математических соотношений между объектами природы и техники. Даже очень сложные системы описываются простыми математическими уравнениями.
F = m*a
Модели имеют ряд функций которые изложим ниже:
А. Обьяснительная функция
1 Модель как вспомогательное звено в объяснении факта теорией
2. Объяснение теории теорией
Б. Предсказательная функция
1.Предсказание неизвестных свойств оригинала
2. Предсказание неизвестных обьектов
3.Предсказание неизвестных закономерностей
В. Критериальные функции
1.Экспериментальные проверки гипотезы и следствий из нее
2.Проверка истинности теории посредством другой теории
Г.Прочие функции
1.Классификационные
2.Вычислительные
3.Демонстрационные
4.Предсказание неизвестных свойств оригинала
Понятие о модели и моделировании. Формирование модели
Модель - это вещественное отображение чего-либо.
Явление®образ®формулизация образа®модель
Самый сложный переход - это переход от явления к образу. Это творческий процесс, он связан с эмоциональными, личностными, интеллектуальными качествами человека.
Для облегчения формулизации задачам моделирования технико-экономических процессов существует системный анализ. Наиболее полно проводят анализ по американской и российской методике.
Формулизация и решение задачи происходит по следующей схеме:

Программе на языке программирования предшествует алгоритм.
Алгоритм - это детерминированная последовательность логических и математических операций.
Алгоритму предшествуют модели, модели предшествует образ, образу предшествует наблюдение явления и осмысление явления.
Любой закон природы это модель.
Модель - это отображение одного предмета другим.
Математическая модель это отображение какого-либо явления или предмета формулой. Любая формула отражает модель. В любую формулу заложен образ явления.
Физическая модель - основана на аналоговых принципах. Например, химическая реакция может быть описана как движение тока, при условии разделения проводящих участков. Константы скорости и электрические сопротивления аналоги.
Логические модели - это последовательность различных операций, которые отображают связями.
Алгоритм - это логическая модель.
Чтобы написать программу надо заложить две модели: логическую и математическую.
Созданию базы данных предшествует разработка логической модели и предметной области.
Абстрактные модели. Абстрактная модель необязательно записывается в виде формулы.
Формализация математических моделей (принцип "черного ящика").
Под "черным ящиком" подразумевается система, о которой известна только ее реакция на входные параметры. Необходимо получить информацию о системе и смоделировать ее.
 Х1 Y1
Х1 Y1
 ¼ ¼
¼ ¼ Хn Yn


Найти математическую взаимосвязь между множеством входных и выходных параметров.
Задача математического моделирования - найти функциональную связь между определенными значениями каких-либо характеристик системы.
В нефтепеработке успешно применяется моделирование процессов и аппаратов, заменяя дорогостоящие эксперименты на реальных моделях (пилотных установках) моделированием с помощью компьютерных программ отечественных и зарубежных.
Вопросы по теме лекции 4:
Моделирование как метод познания.
- Модели материальные и модели информационные.
- Системный подход к окружающему миру.
- Объект и его свойства.
- Система как целостная совокупность объектов элементов).
- Объектно-ориентированное моделирование.
- Построение формальных моделей с использованием формальных языков (алгебры, алгебры логики, языков программирования).
- Построение и исследование с помощью компьютера информационных моделей из физики, биологии, экономики, экологии и др.
Лекция 5. Компьютер и программное обеспечение
